Simetrie circulară
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
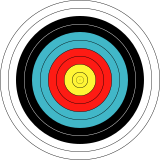 În bidimensional, o țintă de tras cu arcul are simetrie circulară |
 În tridimensional, o suprafață de revoluție are simetrie circulară în jurul unei axe |
În geometrie simetria circulară este un tip de simetrie continuă pentru un obiect plan care poate fi rotit cu un unghi arbitrar și aplicat pe el însuși.
Simetria circulară de rotație este izomorfă cu grupul cercului(d) în planul complex sau grupul ortogonal special SO(2) și grupul unitar(d) U(1). Simetria circulară reflexivă este izomorfă cu grupul ortogonal O(2).
În bidimensional
[modificare | modificare sursă]Un obiect bidimensional cu simetrie circulară ar fi format din domenii cercuri concentrice și coroane circulare.
Simetria circulară de rotație are toate simetriile ciclice(d), Zn, ca simetrii de subgrup. Simetria circulară reflexivă are toate simetriile diedrale, Dihn, ca subgrupuri.
În tridimensional
[modificare | modificare sursă]
În tridimensional o suprafață de revoluție are simetrie circulară în jurul unei axe, numită și simetrie cilindrică. Un exemplu este un con circular drept. Simetria circulară în tridimensional are toate simetriile piramidale, Cnv ca subgrupuri.
Un con dublu (vârf la vârf), bicon, cilindru, toroid și sferoid au simetrie circulară, iar în plus au o simetrie bilaterală, perpendiculară pe axa sistemului. Aceste simetrii circulare cu reflexie au toate simetriile prismatice, Dnh, ca subgrupuri.
În cvadridimensional
[modificare | modificare sursă]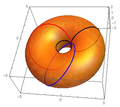 (simplu) |
 1:5 |
 5:1 |
| Cilindrică | Duocilindrică | |
|---|---|---|
În cvadridimensional un obiect poate avea simetrie circulară în două plane de axe ortogonale, sau simetrie duocilindrică. De exemplu, duocilindrul și torul Clifford(d) au simetrie circulară în două axe ortogonale. Un sferindru are simetrie sferică într-un spațiu tridimensional și simetrie circulară în direcția ortogonală.
Simetrie sferică
[modificare | modificare sursă]
Un termen echivalent în spațiul tridimensional este simetrie sferică.
Simetria sferică de rotație este izomorfă cu grupul de rotație SO(3)(d) și poate fi parametrizată prin rotații înlănțuite(d) cu unghiurile de tangaj, ruliu și girație. Simetria sferică de rotație are toate grupurile punctuale(d) chirale discrete ca subgrupuri. Simetria sferică reflexivă este izomorfă cu grupul ortogonal O(3) și are ca subgrupuri grupurile punctuale discrete din spațiul tridimensional.
Bibliografie
[modificare | modificare sursă]- en Eric W. Weisstein, Solid of Revolution la MathWorld.
- en Eric W. Weisstein, Surface of Revolution la MathWorld.
- en Hazewinkel, Michiel, ed. (), „Orthogonal group”, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104

