Công thức Viète

Trong toán học, công thức Viète là một công thức tích vô hạn biểu diễn giá trị của hai lần nghịch đảo hằng số toán học
Nhà toán học người Pháp François Viète công bố công thức vào năm 1593, và công thức này được đặt theo tên ông.[1] Công thức Viète biểu diễn một hằng số bằng một chuỗi các phép tính dài vô hạn,[2] nó cũng có thể biểu thị ý nghĩa chặt chẽ về mặt giới hạn,[3] và cũng đánh dấu sự khởi đầu của giải tích toán học. Công thức này có một tốc độ hội tụ xác định, để từ đó có thể được sử dụng để tính số
Công thức Viète có thể được coi như một kết quả của chuỗi lồng nhau của cả chu vi và diện tích của một đa giác đều trong quá trình suy biến trở thành đường tròn. Cũng bằng việc sử dụng liên tục các công thức nhân đôi góc của lượng giác để suy ra các công thức tổng quát, Leonhard Euler đã thu được công thức Viète như một trường hợp đặc biệt của các công thức tổng quát nêu trên.
Dẫn nhập
[sửa | sửa mã nguồn]François Viète (sinh năm 1540, mất năm 1603) là một luật sư người Pháp, làm việc trong viện cơ mật cho hai đời vua Pháp và là một nhà toán học nghiệp dư. Ông lần đầu tiên công bố công thức Viète vào năm 1593 trong công trình nghiên cứu Variorum de rebus mathematicis responsorum, liber VIII (dịch từ tiếng Latinh: Đáp án cho các vấn đề toán học, cuốn VIII). Trong thời gian này, các phương pháp nhằm tính xấp xỉ số
Bằng việc công bố phương pháp tính của mình dưới dạng một công thức toán học, Viète lần đầu tiên đưa ra một ví dụ mà ngày nay được định nghĩa là tích vô hạn trong toán học,[7][8] và cũng là ví dụ đầu tiên mà một công thức cụ thể có thể tính toán giá trị chính xác của số
Viète sử dụng công thức của chính mình để tính toán số
Công thức Viète không chỉ quan trọng về mặt toán học hay lịch sử toán học, mà còn có thể được sử dụng để giải thích cho sự tán sắc trong một hệ có vô số lò xo với khối lượng cho trước, để từ đó sự xuất hiện của số
Sự hội tụ của công thức Viète
[sửa | sửa mã nguồn]Công thức Viète có thể được biểu diễn dưới dạng kết quả của một phép tính giới hạn[3] mà ở đó dãy số được cho bởi công thức truy hồi
Với mỗi giá trị xác định, biểu thức giới hạn là một phép tính hữu hạn các nhân tử, tuy nhiên khi tiến dần tới vô cùng, kết quả giới hạn này càng ngày càng gần hơn tới kết quả của công thức Viète. François Viète đã nghiên cứu công thức Viète trước cả khi khái niệm về giới hạn và các chứng minh về sự hội tụ trong toán học ra đời; khi mà chứng minh đầu tiên cho việc tồn tại giới hạn nêu trên mới được tìm ra lần đầu tiên trong nghiên cứu của Ferdinand Rudio vào năm 1891.[1][14]

Tốc độ hội tụ của một phép tính giới hạn có liên quan mật thiết tới số lượng biểu thức tham gia phép tính để đạt được một độ chính xác nhất định về mặt số chữ số trong một phép tính. Đối với công thức Viète, số lượng nhân tử và số chữ số tỉ lệ thuận với nhau, và kết quả của công thức Viète cho nhân tử đầu tiên cho ra xấp xỉ số
Công thức liên quan
[sửa | sửa mã nguồn]Công thức Viète có thể được coi như một trường hợp đặc biệt cho công thức liên quan tới hàm sinc. Nhà toán học Leonhard Euler được cho là người tìm ra[16] công thức này hơn một thế kỷ sau đó:[1]
Thay x =
Sau đó, biểu diễn từng nhân tử ở vế phải sử dụng công thức nhân đôi góc:
cho ta công thức Viète.[9]
Ta cũng có thể thu được từ công thức Viète một công thức biểu thị trực tiếp giá trị của số
Công thức này có thể được thu gọn lại dưới dạng dãy số:
Nhiều công thức cho số
Nguồn gốc
[sửa | sửa mã nguồn]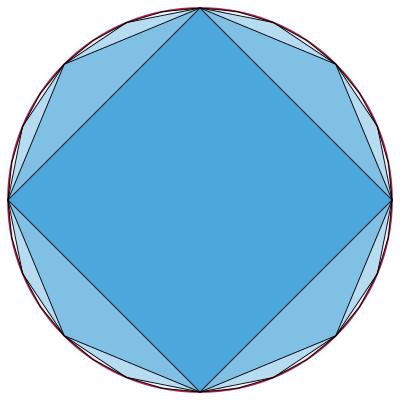
Viète thu được công thức này khi so sánh diện tích của các đa giác đều với số cạnh lần lượt là 2n và 2n + 1 cùng nội tiếp một đường tròn.[1][2] Tỉ lệ đầu tiên khi so sánh diện tích của một hình vuông và một hình bát giác là √2/2 – cũng chính là nhân tử đầu tiên trong công thức Viète, nhân tử thứ hai thu được khi so sánh một hình bát giác với một hình 16 cạnh. Theo đó, chuỗi nhân tử này lồng nhau liên tục để cho ra tỉ lệ diện tích giữa hình vuông (đa giác đều đầu tiên) và đường tròn (trường hợp giới hạn của một đa giác có 2n cạnh). Ngoài ra, các nhân tử xuất hiện trong chuỗi phép nhân vô hạn cũng thể hiện tỉ lệ của chu vi chuỗi đa giác như cách lập luận trên.[25]
Một cách khác để thu được công thức Viète được dựa trên các đẳng thức lượng giác và công thức Euler. Bằng việc liên tục sử dụng công thức nhân đôi góc
dẫn tới việc đưa ra một chứng minh bằng phép quy nạp rằng với mọi số nguyên n,
Biểu thức 2n sin x/2n tiến dần tới x khi mà x trong phép giới hạn tiến dần tới dương vô cùng. Bằng việc thay x =
Xem thêm
[sửa | sửa mã nguồn]Tham khảo
[sửa | sửa mã nguồn]- ^ a b c d e Beckmann, Petr (1993). A history of [pi] (pi) . New York: Barnes & Noble. tr. 94–95. ISBN 0-88029-418-3. OCLC 28616481.
- ^ a b c Maor, Eli (2011). Trigonometric Delights. Princeton: Princeton University Press. tr. 50, 140. ISBN 978-1-4008-4282-7. OCLC 769343155.
- ^ a b Eymard, Pierre (2004). The number [pi]. J. P. Lafon. Providence, R.I.: American Mathematical Society. tr. 44–46. ISBN 0-8218-3246-8. OCLC 53434668.
- ^ a b c d Kreminski, Rick (tháng 6 năm 2008). “
π to Thousands of Digits from Vieta's Formula”. Mathematics Magazine (bằng tiếng Anh). 81 (3): 201–207. doi:10.1080/0025570X.2008.11953549. ISSN 0025-570X. - ^ a b Cullerne, J P; Dunn Goekjian, M C (tháng 1 năm 2012). “Teaching wave propagation and the emergence of Viète's formula”. Physics Education. 47 (1): 87–91. doi:10.1088/0031-9120/47/1/87. ISSN 0031-9120.
- ^ Beckmann, Petr (1993). A history of [pi] (pi) . New York: Barnes & Noble. tr. 67. ISBN 0-88029-418-3. OCLC 28616481.
- ^ De Smith, Michael John (2006). Maths for the mystified : an exploration of the history of mathematics and its relationship to modern-day science and computing. Leicester, U.K.: Matador. tr. 165. ISBN 978-1-905237-81-4. OCLC 123080375.
- ^ a b Moreno, Samuel G.; García-Caballero, Esther M. (tháng 10 năm 2013). “On Viète-like formulas”. Journal of Approximation Theory (bằng tiếng Anh). 174: 90–112. doi:10.1016/j.jat.2013.06.006.
- ^ a b c Morrison, Kent E. (tháng 10 năm 1995). “Cosine Products, Fourier Transforms, and Random Sums”. The American Mathematical Monthly. 102 (8): 716. doi:10.2307/2974641.
- ^ Oldham, Keith B. (2009). An atlas of functions : with Equator, the atlas function calculator. Jan C. Myland, Jerome Spanier, Jerome Preceded by: Spanier. New York, NY. tr. 15. ISBN 978-0-387-48807-3. OCLC 656394964.
- ^ Plofker, Kim (2009). Mathematics in India. Princeton: Princeton University Press. tr. 221–234. ISBN 978-1-4008-3407-5. OCLC 650305544.
- ^ a b c Borwein, Jonathan M. (2014), Sidoli, Nathan; Van Brummelen, Glen (biên tập), “The Life of
π : From Archimedes to ENIAC and Beyond”, From Alexandria, Through Baghdad (bằng tiếng Anh), Berlin, Heidelberg: Springer Berlin Heidelberg, tr. 531–561, doi:10.1007/978-3-642-36736-6_24, ISBN 978-3-642-36735-9, truy cập ngày 27 tháng 1 năm 2023 - ^ a b Dajani, Karma (2002). Ergodic theory of numbers. Cor Kraaikamp. [Washington, DC]. tr. 1–12. ISBN 978-1-61444-027-7. OCLC 877868949.
- ^ Abidoye, Rotimi Boluwatife; Chan, Albert P.C. (4 tháng 7 năm 2016). “Critical determinants of residential property value: professionals' perspective”. Journal of Facilities Management. 14 (3): 283–300. doi:10.1108/jfm-02-2016-0003. ISSN 1472-5967.
- ^ Osler, T. J. (15 tháng 1 năm 2007). “A simple geometric method of estimating the error in using Vieta's product for
π ”. International Journal of Mathematical Education in Science and Technology (bằng tiếng Anh). 38 (1): 136–142. doi:10.1080/00207390601002799. ISSN 0020-739X. - ^ Trong nghiên cứu của Leonhard Euler vào năm 1738: variis modis circuli quadraturam numeris proxime exprimendi[liên kết hỏng] - Về các phương pháp khác nhau để biểu thị cầu phương, công thức hàm sinc là công thức cuối cùng trong nghiên cứu đó. Một công thức tương tự cũng xuất hiện trong một nghiên cứu vào năm 1783: observationes circa angulos in progressione geometrica progredientes[liên kết hỏng] - Các góc nhìn khác nhau về góc với cấp số nhân
- ^ Wilson, Robin J. (2018). Euler's pioneering equation: the most beautiful theorem in mathematics (PDF) . Oxford, United Kingdom. tr. 57–58. ISBN 9780198794929. Bản gốc (PDF) lưu trữ ngày 20 tháng 9 năm 2022. Truy cập ngày 27 tháng 1 năm 2023.
- ^ Servi, L. D. (tháng 4 năm 2003). “Nested Square Roots of 2”. The American Mathematical Monthly. 110 (4): 326. doi:10.2307/3647881.
- ^ Servi, L. D. (tháng 4 năm 2003). “Nested Square Roots of 2”. The American Mathematical Monthly. 110 (4): 326. doi:10.2307/3647881.
- ^ Nyblom, M.A. (1 tháng 4 năm 2012). “Some closed-form evaluations of infinite products involving nested radicals”. Rocky Mountain Journal of Mathematics. 42 (2): 751–758. doi:10.1216/RMJ-2012-42-2-751. ISSN 0035-7596.
- ^ Levin, Aaron (1 tháng 6 năm 2006). “A Geometric Interpretation of an Infinite Product for the Lemniscate Constant”. The American Mathematical Monthly (bằng tiếng Anh). 113 (6): 510. doi:10.2307/27641976.
- ^ Levin, Aaron (tháng 12 năm 2005). “A New Class of Infinite Products Generalizing Viète's Product Formula for
π ”. The Ramanujan Journal (bằng tiếng Anh). 10 (3): 305–324. doi:10.1007/s11139-005-4852-z. ISSN 1382-4090. - ^ Stolarsky, Kenneth (1 tháng 7 năm 1980). “Mapping properties, growth, and uniqueness of Vieta (infinite cosine) products”. Pacific Journal of Mathematics (bằng tiếng Anh). 89 (1): 209–227. doi:10.2140/pjm.1980.89.209. ISSN 0030-8730.
- ^ F. S. M.; E. H. N.; Anderson, W. C. F. (tháng 10 năm 1930). “W. J. Greenstreet”. The Mathematical Gazette (bằng tiếng Anh). 15 (209): 181–185. doi:10.1017/S0025557200137258. ISSN 0025-5572.
- ^ Rummler, Hansklaus (tháng 11 năm 1993). “Squaring the Circle with Holes”. The American Mathematical Monthly. 100 (9): 858. doi:10.2307/2324662.
Liên kết ngoài
[sửa | sửa mã nguồn]- Tác phẩm Variorum de rebus mathematicis responsorum, liber VIII (công bố lần đầu năm 1593) của François Viète trên nền tảng Google Books. Công thức Viète nằm ở nửa sau của trang 30.













![{\displaystyle {\begin{aligned}\pi &=\lim _{k\to \infty }2^{k}{\sqrt {2-a_{k}}}\\[5px]a_{1}&=0\\a_{k}&={\sqrt {2+a_{k-1}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07fce67f7fb709590a7b8bfe4d62fa2c401503fe)


