维基百科,自由的百科全书
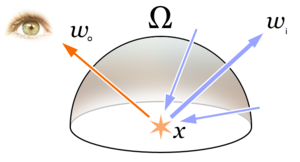 渲染方程描述從x點沿某一方向看的光放射的總額。
渲染方程描述從x點沿某一方向看的光放射的總額。
在计算机图形学领域,渲染方程(Rendering equation)描述的是光能在场景中的流动。根据光学的物理学原理,它在理论上给出了一个完美的结果,而各种各样的渲染技术,只是这个理想结果的一个近似。渲染方程于1986被吉姆·卡吉雅[1] 与 David Immel et al.[2]同时提出。
渲染方程的物理基础是能量守恒定律。在一个特定的位置和方向,出射光 Lo 是发射光 Le 与反射光之和,反射光本身是各个方向的入射光 Li 之和乘以表面反射率及入射角。
这个方程可以用下面的数学等式表示:

其中,
 是在特定位置
是在特定位置  及角度
及角度  的出射光。
的出射光。 是在同一位置及方向发出的光。
是在同一位置及方向发出的光。 是入射方向半球的无穷小累加和。
是入射方向半球的无穷小累加和。 是在该点从入射方向到出射方向光的反射比例。
是在该点从入射方向到出射方向光的反射比例。 是该点的入射光位置及方向
是该点的入射光位置及方向  。
。 是入射角带来的入射光衰减。
是入射角带来的入射光衰减。
它的两个很显然的特性是:线性和空间同质性。由于只有乘法和加法运算,所以是线性的;由于在所有的位置和方向都一样,所以具有空间同质性。这也就意味着方程的解可以有很大范围的因数与排列。
渲染方程是渲染领域中的一个核心理论概念,它是渲染中不可感知方面的最抽象的正式表示。这个方程经过交叉点将出射光线与入射光线联系在一起,它代表了场景中全部的'光线传输'。所有更加完善的算法都可以看作是这个方程的特殊形式的解。
- ^ Kajiya, James T., The rendering equation (PDF), Siggraph 1986, 1986: 143–150 [2019-05-16], ISBN 978-0-89791-196-2, doi:10.1145/15922.15902, (原始内容存档 (PDF)于2021-04-14)
- ^ Immel, David S.; Cohen, Michael F.; Greenberg, Donald P., A radiosity method for non-diffuse environments (PDF), Siggraph 1986, 1986: 133 [2019-05-16], ISBN 978-0-89791-196-2, doi:10.1145/15922.15901, (原始内容存档 (PDF)于2016-08-24)











