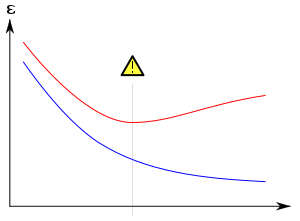
绿线代表 だいひょう 合 あい 模型 もけい 黑 くろ 代表 だいひょう 正 せい 模型 もけい 完 かん 美的 びてき 符合 ふごう 数 すう 据 すえ 但 ただし 得 え 太 ぶと 密 みつ 或 ある 精 せい 黑 くろ 比 ひ 在 ざい 新 しん 的 てき 数 すう 据 すえ 上 うえ 会 かい 有 ゆう 更 さら 高 だか 的 てき 率 りつ 在 ざい 统计学 がく 中 なか 过拟合 あい (英 えい overfitting 或 ある 称 しょう 拟合过度 )是 ぜ 指 ゆび 或 ある 精 せい 匹 ひき 配 はい 特定 とくてい 数 すう 据 すえ 集 しゅう 法 ほう 良好 りょうこう 地 ち 数 すう 据 すえ 或 ある 未来 みらい 的 てき 的 てき 现象 。[ 1] 过拟合 あい 模型 もけい 指 ゆび 的 てき 是 ぜ 相 しょう 限 げん 的 てき 数 すう 据 すえ 参 さん 数 すう 或 ある 者 もの 的 てき 统计模型 もけい 。[ 2] 合 あい 模型 もけい 的 てき 偏差 へんさ 小 しょう 方 かた 差 さ 大 だい 合 あい 的 てき 本 ほん 算法 さんぽう 统计噪声 中 ちゅう 不 ふ 自 じ 了 りょう 信 しん 息 いき 了 りょう 模型 もけい 的 てき 参 まいり 数 すう 当 とう 中 なか [ 3] :45 相 あい 数 すう 据 すえ 来 らい 是 ぜ 可 か 美 び 地 ち 数 すう 据 すえ 的 てき 合 あい 奥 おく 剃刀 かみそり 原 はら
与 あずか 合 ごう 相 しょう 的 てき 概念 がいねん 是 ぜ 欠 かけ 英 えい underfitting 或 ある 称 しょう 拟合不足 ふそく );它是指 ゆび 相 しょう 数 すう 据 すえ 模型 もけい 参 さん 数 すう 或 ある 者 もの 模型 もけい 法 ほう 捕捉 ほそく 到 いた 数 かず 据 すえ 中 ちゅう 的 てき 的 てき 欠 かけ 模型 もけい 的 てき 偏差 へんさ 大 だい 差 さ 小 しょう
在 ざい 机 つくえ 器 き 学 がく 或 ある 人工 じんこう 神 しん 中 なか 合 あい 与 あずか 欠 かけ 有 ゆう 被 ひ 称 しょう 英 えい overtraining )”和 かず 欠 かけ 英 えい undertraining )”。
之 これ 所以 ゆえん 存在 そんざい 合 あい 的 てき 可能 かのう 是 ぜ 因 いん 选择模型 もけい 的 てき 和 わ 模型 もけい 的 てき 是 ぜ 不一致 ふいっち 的 てき 来 らい 模型 もけい 在 ざい 训练数 すう 据 すえ 上表 じょうひょう 好 このみ 的 てき 模型 もけい 但 ただし 模型 もけい 是 ぜ 模型 もけい 在 ざい 中 ちゅう 不可 ふか 据 すえ 上 じょう 的 てき 表 ひょう 当 とう 模型 もけい 数 すう 据 すえ 据 すえ 中 なか 学 がく 可能 かのう 合 あい 一般 いっぱん 来 らい 当 とう 参 さん 数 すう 的 てき 自由 じゆう 度 ど 或 ある 模型 もけい 的 てき 度 ど 超 ちょう 据 すえ 所 しょ 包含 ほうがん 信 しん 息 いき 内容 ないよう 后 きさき 的 てき 模型 もけい 可能 かのう 使用 しよう 任意 にんい 多 た 的 てき 参 さん 数 すう 降 くだ 低 ひく 或 ある 破 やぶ 型 がた 的 てき 能力 のうりょく
在 ざい 学 がく 机 つくえ 器 き 学 がく 或 ある 合 あい 使用 しよう 的 てき 技巧 ぎこう 模型 もけい 交叉 こうさ 提 ひさげ 前 ぜん 停止 ていし 正 せい 剪枝 、贝叶斯信息 いき 量 りょう 准 じゅん 、赤池 あかいけ 信 しん 息 いき 量 りょう 准 じゅん 或 ある dropout )。在 ざい 中 ちゅう 使用 しよう 最小 さいしょう 最 さい 佳 けい 支持 しじ 英 えい minimum best support value )来 らい 合 あい [来 らい 源 みなもと 方法 ほうほう 大 だい 分 ぶん 型 がた 的 てき 度 ど 的 てき 模型 もけい 在 ざい 数 すう 据 すえ 上 じょう 模型 もけい 的 てき 效果 こうか 模 も 型 がた 在 ざい 工作 こうさく 的 てき 数 すう 据 すえ 上 じょう 的 てき 表 ひょう
监督学 がく 例 れい 神 かみ 中 ちゅう 的 てき 合 あい 用 よう 表示 ひょうじ 用 よう 表示 ひょうじ 若 わか 下降 かこう 但 ただし 上 じょう 升 ます 明 あかり 可能 かのう 出 で 最 さい 佳 けい 模型 もけい 是 ぜ 位 い 最低 さいてい 点 てん 模型 もけい 机 つくえ 器 き 学 がく 型 がた 的 てき 典型 てんけい 是 ぜ 由 よし 机 つくえ 器 き 学 がく 算法 さんぽう 在 ざい 训练集 しゅう 上 うえ 希望 きぼう 得 え 到 いた 的 てき 模型 もけい 能 のう 中 ちゅう 不可 ふか 集 しゅう 上表 じょうひょう 良好 りょうこう 合 あい 在 ざい 使用 しよう 奥 おく 剃刀 かみそり 原 はら 模型 もけい 或 ある 算法 さんぽう 当 とう 相 しょう 据 すえ 集 しゅう 的 てき 参 まいり 数 すう 或 ある 使用 しよう 相 しょう 据 すえ 集 しゅう 的 てき 模型 もけい
假 かり 一 いち 基 もと 准 じゅん 真相 しんそう y 可 か 易 えき 数 すう 只 ただ 有 ゆう 数 すう 一 いち 斜 はす 率 りつ 将 はた 数 すう 替 がえ 更 さら 奥 おく 剃刀 かみそり 表明 ひょうめい 相 そう 的 てき 函数 かんすう 任 にん 何 なん 的 てき 函数 かんすう 的 てき 都 と 更 さら 不可 ふか 靠 もたれ [ 4] :358 如果最 さい 函数 かんすう 函数 かんすう 在 ざい 数 すう 据 すえ 数 すう 函数 かんすう 的 てき 收益 しゅうえき 没 ぼつ 有 ゆう 模型 もけい 度 ど 的 てき 增加 ぞうか 那 な 数 すう 了 りょう 数 すう 据 すえ 尽 つき 管 かん 函数 かんすう 在 ざい 集 しゅう 上 じょう 的 てき 表 ひょう 函数 かんすう 相 しょう 同 どう 更 さら 好 このみ 但 ただし 在 ざい 数 すう 据 すえ 之 の 外的 がいてき 数 すう 据 すえ 上 じょう 的 てき 表 ひょう 函数 かんすう 可能 かのう 会 かい 更 さら 糟 かす [ 5]
在 ざい 模型 もけい 度 ど 地 ち 各 かく 模型 もけい 中 ちゅう 参 さん 数 すう 的 てき 数量 すうりょう 是 ぜ 不可 ふか 靠 もたれ 的 てき 要 よう 考 こう 数 すう 的 てき 表 ひょう 式 しき 来 らい 直接 ちょくせつ 比 ひ 有 ゆう m 数 すう 的 てき 神 かみ 和 かず n 数 すう 的 てき 回 かい 型 がた 是非 ぜひ 平凡 へいぼん 的 てき [ 5]
过拟合 あい 尤 ゆう 容易 ようい 在 ざい 次数 じすう 相 しょう 限 げん 的 てき 模型 もけい 会 かい 数 すう 据 すえ 中 ちゅう 特 とく 征 せい 的 てき 随 ずい 机 つくえ 目 め 数 すう 之 これ 因果 いんが 在 ざい 合 あい 的 てき 中 ちゅう 模型 もけい 在 ざい 上 じょう 的 てき 效果 こうか 会 かい 持 じ 升 ます 但 ただし 在 ざい 中 ちゅう 不可 ふか 数 すう 据 すえ 通常 つうじょう 是 ぜ 集 しゅう 上 じょう 的 てき 效果 こうか 会 かい 更 さら 差 さ 的 てき 例 れい 子 こ 假 かり 一 いち 据 すえ 集 しゅう 包含 ほうがん 了 りょう 零 れい 物品 ぶっぴん 日 び 期 き 人 ひと 容易 ようい 在 ざい 数 すう 据 すえ 集 しゅう 上 じょう 模型 もけい 来 らい 根 ね 据 すえ 日 び 期 き 和 わ 属性 ぞくせい 但 ただし 型 がた 在 ざい 新 しん 数 すう 据 すえ 上 じょう 没 ぼつ 有 ゆう 任 にん 何 なん 性能 せいのう 因 いん 的 てき 再 さい 会 かい 出 で
概括 がいかつ 地 ち 机 つくえ 器 き 学 がく 法 ほう 在 ざい 已 やめ 知 ち 数 すう 据 すえ 上 じょう 在 ざい 新 しん 数 すう 据 すえ 上 じょう 不精 ぶしょう 情 じょう 形 がた 可 か 之 の 人 ひと 直 ちょく 理解 りかい 合 あい 的 てき 可 か 被 ひ 分 ぶん 分 ぶん 与 あずか 将来 しょうらい 有 ゆう 数 すう 据 すえ 与 あずか 将来 しょうらい 的 てき 数 すう 据 すえ 在 ざい 条件 じょうけん 都 と 相 しょう 同 どう 的 てき 情 じょう 的 てき 越 えつ 大 だい 不 ふ 性 せい 越 えつ 高 だか 信 しん 息 いき 中 ちゅう 需要 じゅよう 被 ひ 当 とう 声 ごえ 忽 ゆるがせ 略 りゃく 的 てき 部分 ぶぶん 多 た 的 てき 点在 てんざい 如何 いか 数 すう 据 すえ 被 ひ 忽 ゆるがせ 略 りゃく
能 のう 免 めん 的 てき 机 つくえ 器 き 学 がく 法 ほう 是 ぜ 健 けん 壮 たけし 的 てき 算法 さんぽう
过拟合 あい 最 さい 的 てき 后 きさき 果 はて 在 ざい 集 しゅう 上 じょう 的 てき 效果 こうか 后 きさき 果 はて [ 5]
相 あい 合 あい 的 てき 模型 もけい 的 てき 模型 もけい 集 しゅう 的 てき 每 まい 本中 ほんなか 更 さら 多 た 信 しん 息 いき 收集 しゅうしゅう 不 ふ 必要 ひつよう 的 てき 信 しん 息 いき 可能 かのう 代 だい 高 だか 昂 のぼる 的 てき 或 ある 者 もの 具有 ぐゆう 的 てき 当 とう 信 しん 息 いき 需要 じゅよう 人工 じんこう 或 ある 者 もの 代 だい 拟合过度的 てき 模型 もけい 相 しょう 型 がた 的 てき 可 か 移植 いしょく 性 せい 更 さら 差 さ 地 ち 但 ただし 必要 ひつよう 可 か 徒手 としゅ 方面 ほうめん 的 てき 模型 もけい 只 ただ 能 のう 在 ざい 原始 げんし 数 すう 据 すえ 集 しゅう 上 じょう 模型 もけい 的 てき 重用 じゅうよう 和 わ 理 り 研究 けんきゅう 的 てき 了 りょう 困 こま
^ OxfordDictionaries.com 中 なか overfitting (页面存 そん ,存 そん 互联网档案 あん )的 てき 学 がく 定 てい ^ Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics , Cambridge University Press .
^ Burnham, K. P.; Anderson, D. R., Model Selection and Multimodel Inference 2nd, Springer-Verlag, 2002 Google Scholar .)^ Francesco Pezzella, Mahvash Tavassoli, David Kerr. Oxford Textbook of Cancer Biology. Oxford University Press. ^ 5.0 5.1 5.2 Hawkins, Douglas M. (2004), "The problem of overfitting", Journal of Chemical Information and Modeling