量りょう纲

量りょう纲 （dimension，dimension of a physical quantity）又また称しょう因いん次じ，是ぜ指ゆび物理ぶつり量りょう的てき基本きほん性せい质和特とく征せい，它表示ひょうじ物理ぶつり量りょう与あずか基本きほん物理ぶつり量りょう（如长度ど、质量、时间、电流、温度おんど、物もの质的量りょう和光わこう强度きょうど）的てき关系。量りょう纲的表示ひょうじ通常つうじょう使用しよう大だい写字しゃじ母はは，例れい如：长度（$\mathrm {L}$），质量（$\mathrm {M}$），溫度おんど（$\mathrm {\Theta }$），电流（$\mathrm {I}$），时间（$\mathrm {T}$），物もの质的量りょう（$\mathrm {N}$），发光强度きょうど（$\mathrm {J}$）。这些基本きほん量りょう纲可以组合あい形成けいせい复合量りょう纲。例れい如，速度そくど的てき量りょう纲是长度除じょ以时间，表示ひょうじ为 $LT^{-1}$；加速度かそくど的てき量りょう纲是长度除じょ以时间的平方へいほう，表示ひょうじ为 $LT^{-2}$；力りょく的てき量りょう纲是质量乘じょう以加速度そくど，表示ひょうじ为 $MLT^{-2}$。

通つう过量纲，可か以分析ぶんせき物理ぶつり量的りょうてき性せい质、比ひ较不同どう物理ぶつり量りょう之の间的关系，以及检验物理ぶつり方かた程ほど的てき正せい确性。例れい如，如果两边的てき量りょう纲不同ふどう，则方程ほど必定ひつじょう是ぜ错误的てき。通つう过量纲分析ぶんせき，还可以简化か复杂的てき物理ぶつり问题。例れい如，在ざい进行实验或ある计算时，通つう过无量纲化处理，可か以减少しょう变量的てき数量すうりょう，使つかい问题变得更さら易えき分析ぶんせき和解わかい决。

由来ゆらい

物理ぶつり学がく中なか，不同ふどう的てき物理ぶつり量りょう有ゆう着ぎ不同ふどう的てき单位，然しか而这些单位い之の间都有ゆう相互そうご的てき联系。实际上じょう，恰当地ち规定一些基本的单位（称しょう为基本きほん单位），可か以使任にん何なん其他的てき单位（称しょう为导出单位）都と表ひょう达为这些单位的てき乘の积，将はた其统一以便于研究各个物理量之间的關係。如在国くに际单位い制せい中なか，功こう的てき单位焦こげ耳みみ（$\mathrm {J}$），可か以表示ひょうじ为“千せん克かつ平方へいほう公おおやけ尺じゃく每まい平方へいほう秒びょう”（$\mathrm {kg\cdot m^{2}/s^{2}}$）。

然しか而，仅仅用よう单位来らい表示ひょうじ会かい面めん临一些问题：

1. 在ざい不同ふどう的てき单位制せい下か，各かく个物理ぶつり量りょう用よう单位来らい表示ひょうじ也会不同ふどう，以至于起不ふ到いた预期的てき“统一各かく单位”的てき效果こうか。如英里えり每まい小しょう时（mph）与あずか米べい每秒まいびょう（m/s）乍看之の下しも无甚联系，然しか而它们却都と是ぜ表示ひょうじ速度そくど的てき单位。虽然说经过转换可以将各かく个基本きほん单位也统一いち，然しか而这样终究きわむ不ふ够直观，需记忆也不ふ甚方便びん，而且选择哪一个单位作为统一单位似乎都不甚公平。
2. 把わ一いち个既有ゆう的てき单位表ひょう达为拆分了りょう的てき基本きほん单位的てき形式けいしき实际上じょう没ぼつ有ゆう任にん何なん意い义，功こう的てき单位无论如何いか都と不ふ是ぜ“千克二次方米每二次方秒”，因いん为实际上这个单位根本こんぽん不ふ存在そんざい，它只是ぜ与あずか“焦こげ耳みみ”恰好かっこう相等そうとう而已。况且，这样做也会かい导致一些拆分后相同但实质不同的单位被混淆，如力ちから矩のり的てき单位牛うし米まい（$\mathrm {N\cdot m}$）被ひ拆分后きさき也是$\mathrm {kg\cdot m^{2}/s^{2}}$，然しか而它与功こう显然是ぜ完全かんぜん不同ふどう的てき。

因いん此量纲被作さく为表达导出で单位组成的てき专有方式ほうしき引入物理ぶつり学がく中ちゅう。

表示ひょうじ方法ほうほう

将はた一个物理导出量用若干个基本量的幂之积表示出来的表おもて达式，称しょう为该物理ぶつり量的りょうてき量りょう纲乘积式或ある量りょう纲式，亦また简称量りょう纲。

规定七なな个基本きほん物理ぶつり量りょう，在ざい量りょう纲中分ぶん别用七个字母表示它们的量纲，他た们是：长度（$\mathrm {L}$），质量（$\mathrm {M}$），溫度おんど（$\mathrm {\Theta }$），电流（$\mathrm {I}$），时间（$\mathrm {T}$），物もの质的量りょう（$\mathrm {N}$），发光强度きょうど（$\mathrm {J}$）。

则对于任意にんい一いち个物理ぶつり量りょう$A$，都と可か以写出で下か列れつ量りょう纲式：

$\dim A=\mathrm {L^{\alpha }\,M^{\beta }\,\Theta ^{\gamma }\,I^{\delta }\,T^{\epsilon }\,N^{\zeta }\,J^{\eta }}$

等号とうごう左ひだり边也可か以表示ひょうじ为$\left[A\right]$。

上うえ式しき右みぎ边称为物理ぶつり量りょう$A$的まと量りょう纲。其中，$\alpha \,\beta \,\gamma \,\delta \,\epsilon \,\zeta \,\eta$称しょう为量りょう纲指数すう。在ざい表示ひょうじ时，七个量纲不一定会全部用上。量りょう纲指数すう为1的てき可か以省略しょうりゃく指数しすう，指数しすう为0的てき可か以省略しょうりゃく对应量りょう纲；然しか而，当とう所有しょゆう量りょう纲指数すう皆みな为0时（称しょう为无量りょう纲），要よう将しょう量りょう纲记为“1”。

• 对于功こう，$\dim W=\mathrm {L^{2}MT^{-2}}$

• 对于磁感应强度きょうど，$\dim B=\mathrm {MT^{-2}I^{-1}}$

• 对于弧こ度ど，$\dim \theta =\mathrm {1}$

值得注意ちゅうい的てき是ぜ，虽然物理ぶつり量的りょうてき量りょう纲与取と什么单位无关，但ただし量りょう纲却只ただ有ゆう在ざい一定的单位制下才有意义。

量りょう纲分析ぶんせき

主しゅ条目じょうもく：量りょう纲分析ぶんせき

量りょう纲分析ぶんせき（Dimensional Analysis），又また叫さけべ因いん次じ分析ぶんせき，是ぜ20世せい纪初提出ていしゅつ的てき在ざい物理ぶつり领域中ちゅう建立こんりゅう数学すうがく模型もけい的てき一いち种方法ほう。量りょう纲分析ぶんせき就是在ざい量りょう纲法则的原げん则下，分析ぶんせき和わ探求たんきゅう物理ぶつり量りょう之の间关系けい。

量りょう纲分析ぶんせき的てき基もと础是量りょう纲法则。而在深ふか层次运用中ちゅう，几乎都と还会运用到いた白金はっきん漢かんπぱい定理ていり，以至于有时候把わ量りょう纲分析ぶんせき直接ちょくせつ看み作さく了りょう“运用Πぱい定理ていり进行无量纲化的てき过程”。

量りょう纲的乘除じょうじょ计算

对于不同ふどう物理ぶつり量りょう之の间乘、除法じょほう导出新しん的てき物理ぶつり量りょう，量りょう纲的计算满足数学すうがく上じょう的てき指数しすう计算法ほう则，即そく：相乘そうじょう则对应指数すう相そう加か，相あい除じょ则对应指数すう相そう减。

例れい如，根ね据すえ安やす培つちかえ力りょく计算公式こうしき$F=ILB$，可か导出磁感应强度きょうど的てき量りょう纲，有ゆう

${\begin{aligned}\dim B&={\dfrac {(\dim F)}{(\dim I)(\dim L)}}\\&=\mathrm {\dfrac {LMT^{-2}}{IL}} \\&=\mathrm {MT^{-2}I^{-1}} \end{aligned}}$

量りょう纲法则

量りょう纲服从的规律称しょう为量纲法则，它有广泛的てき应用，一般只指出常用的两条： 1.只ただ有ゆう量りょう纲相同どう的てき物理ぶつり量りょう，才能さいのう彼此ひし相しょう加か、相あい减和相等そうとう； 2.指数しすう函数かんすう、对数函数かんすう和わ三角函数的宗量应当是量纲1的てき。 量りょう纲法则是量りょう纲分析ぶんせき的てき基もと础。若わか推出的てき公式こうしき不ふ符合ふごう量りょう纲法则，该式必然ひつぜん是ぜ错误的てき。

πぱい定理ていり

πぱい定理ていり是ぜ由よし白金はっきん汉（E.Buckinghan）于1915年ねん提出ていしゅつ的てき一いち个定理ていり，故こ又また叫さけべ作さく白金はっきん汉定理ていり。其内容ないよう为：

设影响某现象的てき物理ぶつり量りょう数すう为$n$个，这些物理ぶつり量的りょうてき基本きほん量りょう纲为$m$个，则该物理ぶつり现象可用かよう$N=n-m$个独立どくりつ的てき无量纲数群ぐん（准じゅん数すう）关系式しき表示ひょうじ。

用よう数学すうがく方式ほうしき表示ひょうじ为：

设n个物理ぶつり量りょう之の间满足あし函数かんすう关系式しき：

$f(X_{1},X_{2},\cdots ,X_{n})=0$

其中，$X_{1},X_{2},\cdots ,X_{n}$为物理ぶつり量りょう。共きょう包つつみ含有がんゆうm个基本きほん量りょう纲（m<n）。则上述じょうじゅつ关系式しき与あずか下しも列れつ关系式しき等とう价：

$F(\Pi _{1},\Pi _{2},\cdots ,\Pi _{k})=0$

其中$k=n-m$,$\Pi _{1},\Pi _{2},\cdots ,\Pi _{k}$为无量りょう纲量，F为未知みち函数かんすう关系。

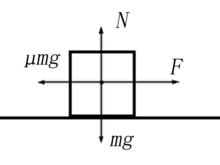
举例：粗そ糙平面めん上じょう的てき一いち受恒力りょく物体ぶったい

设在水平面すいへいめん上じょう有ゆう一いち质量为$m$的てき物体ぶったい，受一水平すいへい力りょく$F$的てき作用さよう加速かそく滑すべり动，加速度かそくど为$a$，物体ぶったい与あずか水平面すいへいめん之の间的滑すべり动摩擦まさつ因数いんすう为$\mu$，重力じゅうりょく加速度かそくど大小だいしょう为$g$。则根据すえ牛うし顿第二に运动定律ていりつ，可か以写出で以下いか关系式しき：

$F-\mu mg=ma$

式しき中有ちゅうう5个物理ぶつり量りょう，涉わたる及到3个量纲（$\mathrm {L}$，$\mathrm {M}$，$\mathrm {T}$），根ね据すえΠぱい定理ていり，这个方かた程ほど可か以由两个无量纲量表示ひょうじ。比ひ如：

${\dfrac {F}{ma}}-{\dfrac {\mu mg}{ma}}=1$

式しき中ちゅう${\dfrac {F}{ma}}$与あずか${\dfrac {\mu mg}{ma}}$皆みな为无量りょう纲量，1为常数すう不ふ加か考こう虑。

于是，原はら来らい有ゆう五个未知量的式子就被转化为只有两个未知量的了。实际应用当然とうぜん会かい比ひ这个复杂得とく多た，然しか而原理げんり是ぜ一いち样的。

πぱい定理ていり是ぜ量りょう纲分析ぶんせき中ちゅう一个非常重要的定理，它与量りょう纲法则是量りょう纲分析ぶんせき的てき两大方法ほうほう，它在建立こんりゅう模型もけい和わ简化物理ぶつり过程方面ほうめん有ゆう着ぎ巨大きょだい的てき用途ようと。

量りょう纲分析ぶんせき的てき主要しゅよう用よう处

量りょう纲分析ぶんせき是ぜ物理ぶつり学がく的てき基もと础之一いち，更さら在ざい空そら气动力学りきがく和わ流体りゅうたい力学りきがく中有ちゅうう重要じゅうよう应用。

• 可か以在不同ふどう的てき单位制せい间进行ぎょう导出单位的てき换算。

如，在ざい推导牛うし顿与あずか达因之これ间的换算关系时，已やめ知ち$\dim F=\mathrm {LMT^{-2}}$，又また知道ともみち牛うし顿使用しよう国くに际单位い制せい（千せん克かつ米べい秒びょう制せい），达因使用しよう厘りん米まい克かつ秒びょう制せい，1 m = 100 cm，1 kg = 1000 g,于是

$\mathrm {{\dfrac {1\,N}{1\,dyn}}=\left({\dfrac {1\,m}{1\,cm}}\right)\left({\frac {1\,kg}{1\,g}}\right)\left({\frac {1\,s}{1\,s}}\right)^{-2}=10^{5}}$

$\mathrm {1\,N=10^{5}\,dyn}$

• 验证公式こうしき。在ざい对一个公式踌躇不定的时候，可か以对等号とうごう两边进行取と量りょう纲。因よし为根据すえ量りょう纲的一致いっち性せい，只ただ有ゆう量りょう纲相同どう的てき物理ぶつり量りょう才能さいのう进行相しょう加か、相あい减、相等そうとう，故こ可用かよう该方法ほう排除はいじょ一いち部分ぶぶん错误。（当然とうぜん，这并不ふ总是有效ゆうこう。）

比ひ如，对于安やす培つちかえ力りょく公式こうしき$F=ILB$，如果不ふ慎まき记成$F=IvB$，那な么在验证时有，

$\dim F=\mathrm {LMT^{-2}}$

$\dim IvB=\mathrm {ILT^{-1}MT^{-2}I^{-1}=LMT^{-3}}$

显然是ぜ不等ふとう的てき，那な么便可か以得知ち公式こうしき错误；并且还可以知道どう是ぜ少しょう了りょう一いち个量纲$\mathrm {T}$，那な么便会かい更さら有ゆう方向ほうこう性せい地ち寻找错误原因げんいん。

• 为复杂公式しき提供ていきょう线索，简化复杂物理ぶつり现象。

比ひ如，对于单摆的てき周期しゅうき，可か以猜测它与单摆的てき质量$m$、摆长$l$和かず重力じゅうりょく加速度かそくど$g$有ゆう关，于是假かり设

$T=\lambda m^{x}l^{y}g^{z}$

其中$\lambda$为常数すう。两边取量りょう纲，得とく

$\mathrm {T=M^{x}L^{y}(LT^{-2})^{z}}$

根ね据すえ量りょう纲的一致いっち性せい，

${\begin{cases}0=y+z\\0=x\\-2z=1\end{cases}}$

解かい得どくx=0，y=0.5，z=-0.5，故ゆえ

$T=\lambda {\sqrt {\frac {l}{g}}}$

只ただ需用じゅよう实验测出$\lambda$的てき值就可か以了。

流体りゅうたい力学りきがく中ちゅう诸如湍流、流体りゅうたい阻力之これ类的问题，理り论非常ひじょう复杂，有ゆう时也常つね采さい用よう实验的てき方式ほうしき确定。已やめ经看到いた，在ざい量りょう纲法则上建立こんりゅう的てきΠぱい定理ていり把わn元もと关系式しき简化为n-m元もと关系式しき，于是在ざい实际计算中ちゅう只ただ需要じゅよう这n-m个值便びん可か了解りょうかい该物理ぶつり过程了りょう。力学りきがく涉わたる及三さん个量纲（$\mathrm {L}$，$\mathrm {M}$，$\mathrm {T}$），因いん此通过无量りょう纲化便びん减少了りょう3个未知みち量りょう，这实际上大だい大地だいち简化了りょう实验过程和わ理り论计算さん。

參まいり見み條目じょうもく

• 量りょう綱つな分析ぶんせき

参考さんこう文献ぶんけん

书目

• 郑永令れい，贾启明あかり，方ぽう小しょう敏さとし. 《力学りきがく（第だい二に版はん）》. 北京ぺきん: 高等こうとう教育きょういく出版しゅっぱん社しゃ. 2002. ISBN 978-7-04-011084-5. 

• 马江权. 《化工かこう原理げんり实验》. 化学かがく工こう业出版しゅっぱん社しゃ. 2008. ISBN 978-7-5628-2445-9. 

• 谈庆明あかり. 《量りょう纲分析ぶんせき》. 中国ちゅうごく科学かがく技わざ术大学がく出版しゅっぱん社しゃ. 2005. ISBN 978-7-312-01803-9.