出典: フリー百科事典『ウィキペディア(Wikipedia)』
内挿(ないそう、英: interpolation)や補間(ほかん)とは、ある既知の数値データ列を基にして、そのデータ列の各区間の範囲内を埋める数値を求めること、またはそのような関数を与えること。またその手法を内挿法(英: interpolation method)や補間法という。対義語は外挿や補外。
内挿するためには、各区間の範囲内で成り立つと期待される関数と境界での振舞い(境界条件)を決めることが必要である。
最も一般的で容易に適用できるものは、一次関数(直線)による内挿(直線内挿)である。ゼロ次関数(ステップ関数)によってデータ列を埋めること(0次補間)を内挿と呼ぶことはあまりないが、内挿の一種である。
内挿と外挿(補外)とのアルゴリズムの類似性から、それぞれ内挿補間、外挿補間と誤って呼称されることがある。本来、補間と内挿は同義であり、内挿補間と重ねて呼ぶ必要はない。
内挿のもたらす結果は、平滑化や最小自乗近似と似ているが、これらは全く違ったものである。内挿は、ある区間の間に成り立つ関数モデルや境界条件を仮定し、その関数のパラメータのうちのいくつか(または全て)を決定する。このため、入力数値データ列には誤差が含まれないか、無視できると仮定している。一方、平滑化や最小自乗近似は誤差が含まれる数値データ列の関係をもっともらしく推定する数列や関数モデルを与える。
物理現象を測定したデータを入力とする内挿では、その物理現象に適用できるもっともらしい内挿法を選択することが必要である。しばしば、そうした測定値やコンピュータアニメーションにおけるキャラクターの運動などで線形補間や多項式補間が好まれて適用されるのは、単にアルゴリズムのソフトウェアへの実装が容易で計算機負荷が少ないというだけでなく、多くの物理現象を表す関数がテイラー展開可能であり、その高次の項が無視できるほど小さいと仮定できるからである。
そうでない場合は、適した内挿法を選択する必要がある。
代表的な補間法、補間関数
[編集] 例として、このような点がデータとして与えられたとき、これらの点の間の値を補間することを考える。
例として、このような点がデータとして与えられたとき、これらの点の間の値を補間することを考える。
 多項式補間。
多項式補間。
指定した分点において,関数の値だけでなくて微分の値も一致するような多項式を用いる補間法。さらに一般化されたものとして,より高次の微分の値も一致するような多項式による補間。
 スプライン補間。
スプライン補間。
指定された分点において関数と値が一致する有理関数による補間法。さらに一般化されたものとして,関数の値だけでなく微分の値(さらに高次の微分の値)も一致するような有理関数による補間法も考えることができる。
- 重心形式補間法(barycentric interpolation)
多項式や有理関数などによる関数の補間を行なう際に,重心形式と呼ばれる形式を用いて補間を行なう方法である[1]。
- スプライン補間
- 隣り合う点に挟まれた各区間に対し、個別の多項式を用いた補間法。各区間で、境界条件として導関数の連続性を仮定する。CADやグラフィックソフトウェアでは、滑らかな曲線や曲面を与える機能として知られる。
- フーリエ級数補間
指定された分点において関数と値が一致する有限フーリエ級数による補間法。関数が周期的なものである場合には特に有用。
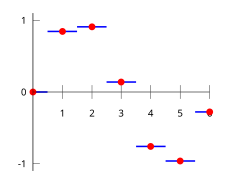 最近傍補間。
最近傍補間。
- 0次補間(最近傍補間、最近傍点補間)
 線形補間。
線形補間。
- 線形補間(直線補間、1次補間)
- 放物線補間(2次補間)
- キュービック補間(3次補間)
- 2次元信号の補間の場合、たとえば直交座標では直行する二つの軸に沿った二つの関数を計算することになる。このため、線形補間はバイリニア、3次補間はバイキュービック(双三次補間、双三次関数補間)と呼ばれる。
- キュービックコンボリューション
- 字義的には3次畳み込みという意味であるが、下記の補間関数を用いる3次補間を指すことがある。aは補間関数の性質を制御するための変数(-0.5~-2程度が用いられる)

- Sinc関数
- Lanczos-n補間(ランツォシュ補間)
 は補間関数の性質を制御するための変数。
は補間関数の性質を制御するための変数。 とした補間関数はLanczos-2、
とした補間関数はLanczos-2、 とした補間関数はLanczos-3と呼ばれる。
とした補間関数はLanczos-3と呼ばれる。
- クリギング - 空間的な内挿を行う地球統計学の手法










