일각형
보이기
| 일각형 | |
|---|---|
 원에서 일각형은 꼭짓점 하나와 360도의 호(모서리)로 이루어진 테셀레이션이다. | |
| 종류 | 정다각형 |
| 모서리들과 꼭짓점 | 1 |
| 슐레플리 기호 | {1} or h{2} |
| 콕서터 다이어그램 | |
| 대칭 그룹 | [ ], Cs |
| 쌍대 다각형 | 자기쌍대 |
기하학에서 일각형은 변과 꼭짓점이 각각 하나인 다각형을 말한다. 일각형의 슐레플리 기호는 {1}이다.[1] 일각형은 변과 각이 각각 하나 뿐이으므로, 이론적으로 모든 일각형은 정일각형이다.
유클리드 기하학에서
[편집]유클리드 기하학에서 일각형은 다른 선분과는 달리 양 끝점이 동일해야 하기 때문에 축퇴 다각형이다. 유클리드 기하학에서 대부분 다각형의 정의는 일각형을 인정하지 않는다.
구면 기하학에서
[편집]구면기하학에서 일각형은 구의 대원에 꼭짓점 하나로 만들 수 있다. 이것은 반구의 일각형 두 개가 꼭짓점 한 개와 360°의 변 하나를 공유하는 이면체 {1,2}를 만든다. 이것의 쌍대인 호소헤드론{2,1}은 두 개의 대척 꼭짓점과 달꼴의 면 하나와 두 꼭짓점 사이에 자오선 모서리를 가지고 있다.[1]
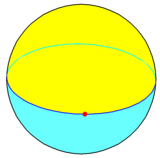 일각형 이면체, {1,2} |
 일각형 호소헤드론, {2,1} |
같이 보기
[편집]각주
[편집]- Herbert Busemann, The geometry of geodesics. New York, Academic Press, 1955
- Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
