Ентропия

Термодинамична система с ниска ентропия

Термодинамична система с висока ентропия

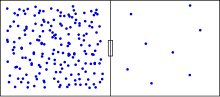
Ентропия е физична величина, която представлява мярка за безпорядъка на термодинамичните системи. Терминът „ентропия“ произхожда от гръцкия език: εいぷしろんνにゅー – вътре, τρέπω – пренасям.

Ентропията характеризира състоянието на термодинамичната система, т.е. зависи само от текущото състояние, а не от това как системата се е озовала в него.

Ентропията е правопропорционална на логаритъма на броя на възможните микросъстояния (конфигурации на градивните частици), съответстващи на дадено макросъстояние на системата. Състоянието на термодинамично равновесие се характеризира с максимална вероятност, максимален безпорядък и максимална ентропия.

Различия с други величини

Вътрешната енергия на системата включва общото количество механична енергия на градивните частици, докато ентропията отчита качественото различие между насочено и хаотично движение на същите частици.

Работата и количеството топлина характеризират процесите, които протичат в системата, а ентропията характеризира състоянието на системата.

Ентропията се различава и от температурата: например при изотермно нагряване температурата остава постоянна, а ентропията на системата нараства.

Газовете имат по-голяма ентропия от течностите и твърдите тела.

Основна закономерност

Ако в изолирана макроскопична система протича термодинамичен процес, то ентропията на системата нараства и процесът е необратим. Всички процеси в природата се подчиняват на този закон (втори принцип на термодинамиката).

История

Понятието „ентропия“ е въведено за първи път през 1865 г. от Рудолф Клаузиус (1822-1888), немски физик, считан за един от създателите на термодинамиката и кинетичната теория на газовете. Той предлага и една от формулировката на втория принцип на термодинамиката.

Теория

Класическа термодинамика

Изменението на ентропията ΔでるたS на термодинамична система при обратими процеси е отношението на изменението на общото количество топлина ΔでるたQ към абсолютната температура Т.

$\Delta S={\frac {\Delta Q}{T}}$

Ентропията се измерва в J/K, а специфичната ентропия – в J/(kg.K).

Названието „ентропия“ е предложено от Клаузиус.

Тази формула е приложима само за изотермни процеси. Обобщението ѝ за произволен квазистатичен процес изглежда така:

$dS={\frac {\delta Q}{T}}$,

където dS е диференциалът на ентропията, а δでるたQ е безкрайно малко количество топлина. Ентропията е характеристика на състоянието, затова в лявата част на равенството стои пълен диференциал. Обратно, количеството топлина е характеристика на процеса, а не на състоянието, затова δでるたQ е непълен диференциал.

Горната формула определя единствено изменението на ентропията, следователно задава ентропията с точност до едно неизвестно събираемо (т. нар. нулево ниво). Третият принцип на термодинамиката допълва определението на ентропията, като уточнява нейното нулево ниво: при температура, равна на абсолютната нула, ентропията на равновесна система също е нула. Това е така, тъй като абсолютната нула на температурата съответства на прекратяване на хаотичното движение на градивните частици на веществото.

Статистическа термодинамика

През 1877 г. Лудвиг Болцман открива, че ентропията S на една система е пропорционална на логаритъма от броя Ωおめが на възможните микросъстояния, съответстващи на дадено макроскопично състояние. В случая на идеален газ микросъстоянието се определя от местоположението и импулса на всяка от градивните частици на системата.

Болцман е установил, че

$S=k\,.\,\ln \Omega$,

където k = 1,38.10^-23 J/К е т. нар. константа на Болцман. Тази формула е част от статистическата термодинамика, която описва термодинамичните системи чрез поведението на съставящите ги компоненти. Формулата на Болцман свързва микроскопичните свойства на системата (броя Ωおめが на микросъстоянията) с едно от нейните макроскопични термодинамични свойства (ентропията S).

От формулата на Болцман се вижда, че ентропията е функция на състоянието. Тъй като Ωおめが може да бъде само естествено число (1, 2, 3 и т.н.), то ентропията може да приема само неотрицателни стойности.

Вижте също

• Втори закон на термодинамиката