| この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)
出典検索?: "ビオ・サバールの法則" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2021年11月) |
ビオ・サバールの法則(ビオ・サバールのほうそく、英: Biot–Savart law)とは電流の存在によってその周りに生じる磁場を計算する為の電磁気学における法則である。この法則は静電場に対するクーロンの法則に対応する。
この法則によって磁場は距離、方向、およびその電流の大きさなどに依存することが論じられる。この法則は静的な近似の元ではアンペールの法則および磁場に対するガウスの法則と同等である。
1820年にフランスの物理学者ジャン=バティスト・ビオとフェリックス・サヴァールによって発見された。
微小な長さの電流要素 I dl によって r 離れた位置に作られる微小な磁場 dH は

で表される。ここで r := |r| である。
電流がある程度の幅をもって流れているとき(すなわち、太さ無限小の線でなく領域 V を占めているとき)、電流密度 j を使った積分形で書く必要がある:

なお上式では左辺の磁場 H は微小量ではない。
この法則は積分を実行して初めて有効な値が出る、すなわち実験的検証が間接的にならざるを得ない欠点がある。
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | この 節の 加筆が 望まれています。 (2011年3月) |
1820年4月、デンマークの物理学者ハンス・クリスティアン・エルステッドはコペンハーゲン大学での講義中、電気回路をいじっていた時近くにあった方位磁石が北ではない方角を指ししていることに気が付き、電流と磁場の関係について数か月の研究の末、電流の磁気作用を発表した。
これを受け、ジャン・バティスタ・ビオとフェリックス・サバールは共同で実験を行い、この法則を発表するに至った。さらにこの数ヵ月後にはフランソワ・アラゴーが電磁石の原理を、アンドレ・マリー・アンペールがアンペールの法則を発見している。これらの功績がエルステッドの発見から僅か一年以内のことであったのは驚くべきことである。
さらに3年後の1823年にスタージャンが実際に電磁石を作成し、24年にアラゴーは回転磁気を発見している。この1820年からの数年間は科学史上重要な期間である。
均一な電流[編集]
電流I が如何なる点においても一定の場合磁場H は、

となる。
等速度運動する点電荷[編集]
点電荷q が一定の速度v で運動しているとき、特殊相対性理論とマクスウェルの方程式より以下の電束密度と磁場が与えられる[1]。

ただし、β = v / c、θ は v とr のなす角であり、c は光速度である。
v が c に対して十分に小さい( )ときは、近似的に
)ときは、近似的に

と表すことができる。
これらの電束密度と磁場に関する式は、点電荷に対するビオ・サバールの法則と呼ばれ、1888年にオリヴァー・ヘヴィサイドによって導かれた。
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | この 節の 加筆が 望まれています。 (2011年3月) |
無限に長い直線電流の周りの磁場[編集]

ビオ・サバールの法則は積分することによりアンペールの法則の磁場と一致する。
例えば無限に長い直線電流であれば、図より、

したがって

となるから、ビオ・サバールの法則を積分して、
![{\displaystyle {\begin{aligned}H&={\frac {1}{4\pi }}\int _{-\infty }^{\infty }{\frac {I\sin \theta }{r^{2}}}\,\mathrm {d} s\\&={\frac {1}{4\pi }}\int _{0}^{\pi }{\frac {I\sin \theta }{r^{2}}}{\frac {a}{\sin ^{2}\theta }}\,\mathrm {d} \theta ={\frac {I}{4\pi }}\int _{0}^{\pi }{\frac {\sin \theta }{a}}\,\mathrm {d} \theta ={\frac {I}{4\pi a}}\left[-\cos \theta \right]_{0}^{\pi }\\&={\frac {I}{2\pi a}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad717043bbffda7e88aa1752441a4946ef17e597)
を得る。これはアンペールの法則の磁場の大きさと一致する。
立体角を用いた解析[編集]
 閉経路C1から回路C2を俯瞰する立体角をΩとする。
閉経路C1から回路C2を俯瞰する立体角をΩとする。
以下のようにしてもビオ・サバールの法則からアンペールの法則が成り立つことを示すことができる[2]。
閉回路C1上の点Pから回路C2を俯瞰する立体角を Ω とする。ここで回路C1上を点Pから微小距離 ds だけ移動した点をP′とすると、点P′から回路C2を俯瞰する立体角Ω+dΩ は、−ds だけ平行移動された回路を俯瞰する立体角と等しい。
このとき、回路上の微小長さ ds′ と平行移動した微小距離 −ds によって作られる面の面素ベクトル dS は

であるが、点Pから回路上の微小長さ ds′ へ向かうベクトルを r とすると、点Pから面素 dS を見る立体角は

と表すことができる。
これを ds′ に関して回路一周分線積分すれば立体角の変化dΩを得ることができる。

回路上の微小電流要素が点Pに作る磁場はビオ・サバールの法則を積分して、

と得られるが、この両辺に ds を内積で乗じ、先の式を代入すると

の関係が得られる。
点Pが閉曲線C1上を一周するようなΩの変化は

であるので、

とする、アンペールの法則そのものが導かれる。
この場合、C1で囲む領域 D(図赤色)の面積を S1とすると、面S1に対する電流面密度の大きさj は

となるが、例えば閉曲線C1が1周する間に回路C2が3周するような場合には電流面密度の大きさは 3j 、閉曲線C1が2周する間に回路C2が1周するような場合には電流面密度の大きさは j/2 である。このことを考慮すれば、

と書くことができる。
円形電流の中心付近に於ける磁場[編集]
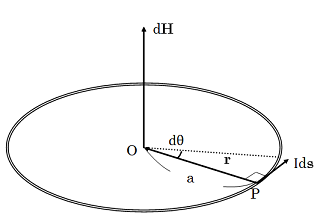 中心に生じる磁場
中心に生じる磁場
アンペールの法則を使った場合では求めることが難しい場合も、ビオ・サバールの法則を用いることで簡易に計算できる場合がある。例えば円形電流の中心付近に発生する磁場を求める場合がそうである。まず、右図のような半径 a の円周上P点に存在する電流 I によって、中心Oに生じる磁場について考える。
ds と r の為す角度を φ とおくと、図より

となり、また

であるので、

である。これを円周上で積分して、

となる。
 中心よりzだけずれた位置に生じる磁場
中心よりzだけずれた位置に生じる磁場
次に、右図のようなOより面に垂直に z だけずれた位置Qに生じる磁場について考える。図より、

である。
dH はビオ・サバールの法則より ds と r に垂直で、面に平行な成分  は対称性により円周上を積分すると 0 になってしまうので、面に垂直な成分
は対称性により円周上を積分すると 0 になってしまうので、面に垂直な成分  のみを考えればよい。
のみを考えればよい。

ここで、ds = a dθ であることを用いて、

ここで、z = 0 とすれば、円の中心部に生じている磁場HO が得られる。即ち、

であり、これは先ほど求めたものに一致する。
発散と回転[編集]
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | この 節の 加筆が 望まれています。 (2011年3月) |
ビオ・サバールの法則の両辺の発散を取る。

ここで、ベクトル解析の恒等式より

また、

なので、これを代入すると、

を得る。これは、磁場に対するガウスの法則より導かれる結果に等しい。
ビオ・サバールの法則の両辺の回転を取る。

ここで、ベクトル解析の恒等式より

また、

なので、

が得られる。これはアンペールの法則そのものである。
ただし、この書き換えは静磁場でのみ有効であることに留意しなければならない。
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | この 節の 加筆が 望まれています。 (2011年3月) |
静磁場で、ベクトルポテンシャルが

と定義出来るとき、

であるので、ベクトルの恒等式、

からビオ・サバールの法則はベクトルポテンシャル A によって

と書き換えられることになる。ここで、 は真空の透磁率、
は真空の透磁率、 は電流密度+磁化電流密度である。
は電流密度+磁化電流密度である。
また、ビオ・サバールの法則は静電場におけるクーロンの法則に対応するものであるが、同様に電場のスカラーポテンシャル φ

によって静電場におけるクーロンの法則、あるいはガウスの法則を書き換えると

となり対称性を見ることができる。ここで は真空の誘電率、
は真空の誘電率、 は電荷密度+分極電荷密度である。
は電荷密度+分極電荷密度である。
マクスウェル方程式からの導出[編集]
もちろん、電磁気学の法則なのでマクスウェル方程式から導出することができる。前節において電場と磁場のそれぞれがスカラーポテンシャルとベクトルポテンシャルによって記述され、しかもかたや電荷密度、かたや電流密度を距離の逆比で重み付けして積分するという形式になっていることをみたが、その対称性の説明もできる。
まずクーロンの法則をマクスウェル方程式から導出するプロセスを考える。これは静電場仮定でのポテンシャルと電場の関係

を用いて、ガウスの法則

を変形すると

が得られる。これを に対する微分方程式だと考えると、グリーン関数法によって解くことができる。すなわち、方程式の両辺をフーリエ変換して、各モードに対するウェイトの方程式として読み替え、ウェイトがわかったところでフーリエ逆変換によって解を構成する。解は前節の通りで
に対する微分方程式だと考えると、グリーン関数法によって解くことができる。すなわち、方程式の両辺をフーリエ変換して、各モードに対するウェイトの方程式として読み替え、ウェイトがわかったところでフーリエ逆変換によって解を構成する。解は前節の通りで

となる。本題のビオ・サバールの法則の場合はアンペール・マクスウェルの法則

をやはり静電場仮定で右辺第二項を無視した上で、ポテンシャル表示

を適用する。すると

となるが、 および、クーロンゲージ
および、クーロンゲージ を適用することで
を適用することで

となる。今度はベクトルになっているが、演算子がスカラーなので各ベクトル成分に対して独立に同じ方程式を立てているに過ぎず、また、式の形上もスカラーポテンシャルの時と係数を除いて同じなので同じ方法を使って構成すれば

を得ることになる。これに回転を取ればビオ・サバールの法則が得られる。
以上のことをまとめると、
- 考えているベクトル場
 が何らかのベクトル場
が何らかのベクトル場 の回転で記述できる(
の回転で記述できる( )
)
- ベクトル場
 の回転がベクトル場
の回転がベクトル場 に比例する
に比例する
- 空間次元が3であるとき(グリーン関数法の結果がこのような重み付けになる上で必要)
ビオ・サバールの法則が(比例係数を除いて)得られることになる。
流体力学[編集]
前節で説明したように、数式上の性質さえ共通すればビオ・サバールの法則を得ることになる。それは具体的には流体力学が好例である。
流体力学における渦度は流速の回転として定義されている。

したがって、渦度の具体的な場 を知ることができ(それ自身なので比例係数1で比例しているとみなす)、
を知ることができ(それ自身なので比例係数1で比例しているとみなす)、 を言える場合には、(もちろん空間次元3の領域で問題を扱うので)
を言える場合には、(もちろん空間次元3の領域で問題を扱うので) からベクトル場
からベクトル場 をビオ・サバールの法則によって記述できる。
をビオ・サバールの法則によって記述できる。
具体的には

という結果を得ることができる。
上記結果を渦糸に適用してその微小部分の寄与を取り出すことで次のように記述されるビオ・サバールの法則をみる[3]。

ただし変数の意味を以下のように読み替える。
- dv :観測点で誘導される速度
- Γ:渦糸まわりの循環
- ds :渦糸の微小部分
- θ:ds の方向とそこから観測点を結ぶ直線とのなす角
- r :ds と観測点の距離
- ^ Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 222–224, 435–440. ISBN 0-13-805326-X
- ^ 伊藤敏夫『朝倉物理学選書2 電磁気学』。ISBN 978-4-254-13757-6。
- ^ 小池勝『流体機械工学』コロナ社、2009年、29頁。ISBN 978-4-339-04474-4。











![{\displaystyle {\begin{aligned}H&={\frac {1}{4\pi }}\int _{-\infty }^{\infty }{\frac {I\sin \theta }{r^{2}}}\,\mathrm {d} s\\&={\frac {1}{4\pi }}\int _{0}^{\pi }{\frac {I\sin \theta }{r^{2}}}{\frac {a}{\sin ^{2}\theta }}\,\mathrm {d} \theta ={\frac {I}{4\pi }}\int _{0}^{\pi }{\frac {\sin \theta }{a}}\,\mathrm {d} \theta ={\frac {I}{4\pi a}}\left[-\cos \theta \right]_{0}^{\pi }\\&={\frac {I}{2\pi a}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad717043bbffda7e88aa1752441a4946ef17e597)


























































