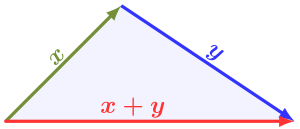
三 さん 辺 へん 長 なが x, y, z とする三角形 さんかっけい 三 さん 例 れい 数学 すうがく 三角 さんかく 不等式 ふとうしき 英 えい triangle inequality 任意 にんい 三角形 さんかっけい 対 たい 任意 にんい 二 に 辺 へん 和 わ 残 のこ 一 いち 辺 へん 大 おお 述 の [1] 三角 さんかく 比 ひ 含 ふく 不等式 ふとうしき 三角 さんかく 不等式 ふとうしき 英 えい trigonometric inequalities 呼 よ 場合 ばあい 指 さ 注意 ちゅうい 必要 ひつよう
(退化 たいか 場合 ばあい 含 ふく 三角形 さんかっけい 三 さん 辺 へん x , y , z 最大 さいだい 辺 あたり z とすれば、三角 さんかく 不等式 ふとうしき
z
≤
x
+
y
{\displaystyle z\leq x+y}
が成 な 立 た 主張 しゅちょう [注釈 ちゅうしゃく
等号 とうごう 成立 せいりつ 三角形 さんかっけい 面積 めんせき 0 に退化 たいか 限 かぎ ユークリッド幾何 きか 学 がく ほかいくつかの幾何 きか 学 がく 三角 さんかく 不等式 ふとうしき 距離 きょり 関 かん 定理 ていり 長 なが ノルム )を用 もち
‖
x
+
y
‖
≤
‖
x
‖
+
‖
y
‖
{\displaystyle \|\mathbf {x} +\mathbf {y} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|}
と書 か 第 だい 三 さん 辺 へん 長 なが z がベクトルの和 わ x + y 置 お 換 か 注意 ちゅうい x, y が実数 じっすう ℝ1 のベクトルと見 み 三角 さんかく 不等式 ふとうしき 絶対 ぜったい 値 ち 間 あいだ 関係 かんけい 記述 きじゅつ
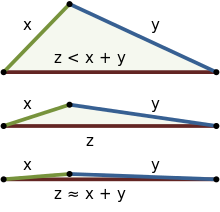
ユークリッド幾何 きか 学 がく 直角 ちょっかく 三角形 さんかっけい 対 たい 三角 さんかく 不等式 ふとうしき 三 さん 平方 へいほう 定理 ていり 帰結 きけつ 一般 いっぱん 三角形 さんかっけい 場合 ばあい 余弦 よげん 定理 ていり 帰結 きけつ 定理 ていり 証明 しょうめい 可能 かのう 三角 さんかく 不等式 ふとうしき ℝ2 や ℝ3 の何 いず 直観 ちょっかん 的 てき 見 み 右 みぎ 図 ず 明 あき 不等号 ふとうごう 成 な 立 た 上 うえ 等号 とうごう 近 ちか 下 した 三 さん 例 れい 幾何 きか 学 がく 場合 ばあい 等号 とうごう 成立 せいりつ 一 ひと 角 かく 180° で二 ふた 角 かく 0° の場合 ばあい 三 さん 頂点 ちょうてん 同 どう 一直線 いっちょくせん 上 じょう 場合 ばあい 限 かぎ 幾何 きか 学 がく 二 に 点 てん 間 あいだ 最短 さいたん 距離 きょり 直線 ちょくせん
球面 きゅうめん 幾何 きか 学 がく 二 に 点 てん 間 あいだ 最短 さいたん 距離 きょり 大円 だいえん 弧 こ 球面 きゅうめん 上 じょう 二 に 点 てん 間 あいだ 距離 きょり 二 に 点 てん 結 むす 劣 れつ 弧線 こせん 分 ぶん 大円 だいえん 中 なか 二 に 点 てん 端点 たんてん 二 ふた 弧 こ 中心 ちゅうしん 角 かく [0, π ぱい のもの)で与 あた 三角 さんかく 不等式 ふとうしき 成 な 立 た
三角 さんかく 不等式 ふとうしき ノルム や距離 きょり 函数 かんすう 定義 ていぎ 性質 せいしつ 一 ひと 性質 せいしつ 各々 おのおの 特定 とくてい 空間 くうかん 実数 じっすう 直線 ちょくせん ユークリッド空間 くうかん や (p ≥ 1対 たい Lp -空間 くうかん 内積 ないせき 空間 くうかん 対 たい 距離 きょり 函数 かんすう 任意 にんい 函数 かんすう 対 たい 定理 ていり 述 の
ユークリッド幾何 きか 学 がく 場合 ばあい [ 編集 へんしゅう ] ユークリッドの平面 へいめん 幾何 きか 三角 さんかく 不等式 ふとうしき 証明 しょうめい 構成 こうせい ユークリッドは平面 へいめん 幾何 きか 三角 さんかく 不等式 ふとうしき 図 ず 構成 こうせい 用 もち 証明 しょうめい 三角形 さんかっけい ABC に対 たい 一 いち 辺 へん BC を共有 きょうゆう 二等辺三角形 にとうへんさんかっけい 一 ひと 等辺 とうへん BD の足 あし 辺 あたり AB の延長 えんちょう 上 じょう 作 つく 角 かく β べーた α あるふぁ 言 い 辺 あたり AD > AC 言 い AD = AB + BD = AB + BC 辺 あたり 和 わ AB + BC > AC ユークリッドの『原論 げんろん I 巻 まき 命題 めいだい 書 か [6]
折線 おれせん 不等式 ふとうしき [ 編集 へんしゅう ] 三角 さんかく 不等式 ふとうしき 数学 すうがく 的 てき 帰納 きのう 法 ほう 任意 にんい 折線 おれせん 関 かん 命題 めいだい 拡張 かくちょう 折線 おれせん 全 すべ 辺 あたり 長 なが 和 わ 折線 おれせん 二 に 端点 たんてん 直線 ちょくせん 結 むす 長 なが 小 ちい 特 とく 帰結 きけつ 多角 たかく 形 がた 長 なが 辺 あたり 残 のこ 全 すべ 辺 あたり 長 なが 和 わ 必 かなら 小 ちい 言 い
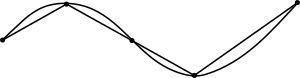
曲線 きょくせん 弧 こ 長 ちょう 折線 おれせん 近似 きんじ 長 なが 上限 じょうげん 定義 ていぎ このように折線 おれせん 対 たい 一般 いっぱん 化 か 幾何 きか 二 に 点 てん 間 あいだ 結 むす 最短 さいたん 曲線 きょくせん 直線 ちょくせん 示 しめ
二 に 点 てん 間 あいだ 結 むす 折線 おれせん 二 に 点 てん 間 あいだ 結 むす 線分 せんぶん 短 みじか 曲線 きょくせん 弧 こ 長 ちょう 曲線 きょくせん 両 りょう 端点 たんてん 間 あいだ 距離 きょり 短 みじか 従 したが 実際 じっさい 定義 ていぎ 曲線 きょくせん 弧 こ 長 ちょう 近似 きんじ 折線 おれせん 長 なが 上限 じょうげん 折線 おれせん 対 たい 結果 けっか 端点 たんてん 間 あいだ 結 むす 線分 せんぶん 全 すべ 折線 おれせん 近似 きんじ 中 なか 最短 さいたん 曲線 きょくせん 弧 こ 長 ちょう 任意 にんい 折線 おれせん 近似 きんじ 長 なが 以上 いじょう 曲線 きょくせん 自身 じしん 直線 ちょくせん 経路 けいろ 短 みじか
高次 こうじ 元 もと 単体 たんたい 不等式 ふとうしき [ 編集 へんしゅう ] 三角 さんかく 不等式 ふとうしき 高 こう 次元 じげん 一般 いっぱん 化 か 空間 くうかん 内 ない n -次元 じげん 単体 たんたい n − 1次元 じげん ファセット の超 ちょう 体積 たいせき 以外 いがい n 個 こ 超 ちょう 体積 たいせき 和 わ 以下 いか 特 とく 四 よん 面体 めんてい 一 ひと 三角形 さんかっけい 面 めん 面積 めんせき 三面 さんめん 面積 めんせき 和 わ 以下 いか
ノルム線型 せんけい 空間 くうかん 場合 ばあい [ 編集 へんしゅう ] ベクトルのノルムに対 たい 三角 さんかく 不等式 ふとうしき ノルム空間 くうかん V に対 たい ノルム を定義 ていぎ 性質 せいしつ 一 ひと 三角 さんかく 不等式 ふとうしき
‖
x
+
y
‖
≤
‖
x
‖
+
‖
y
‖
(
∀
x
,
y
∈
V
)
{\displaystyle \|x+y\|\leq \|x\|+\|y\|\quad (\forall \,x,y\in V)}
である。つまり、二 ふた ベクトルの和 わ (英語 えいご 版 ばん 二 ふた 長 なが 和 わ 抑 おさ 劣 れつ 加法 かほう 性 せい 呼 よ 振 ふ 舞 ま 期待 きたい 任意 にんい 函数 かんすう 要件 ようけん 満足 まんぞく
ノルム空間 くうかん ユークリッド空間 くうかん あるいはより一般 いっぱん 狭義 きょうぎ 凸 とつ 空間 くうかん ‖ x + y ‖ = ‖ x ‖ + ‖ y ‖ となるための必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん 三 さん 点 てん x , y , x + y 成 な 三角形 さんかっけい 退化 たいか x, y が同 どう 一半 いっぱん 直線 ちょくせん 上 じょう 式 しき 書 か x = 0y = 0x = α あるふぁ α あるふぁ 性質 せいしつ 狭義 きょうぎ 凸 とつ 空間 くうかん 例 たと ℓp -空間 くうかん 1 < p < ∞ ) など)を特徴付 とくちょうづ 成立 せいりつ 空間 くうかん 存在 そんざい [注釈 ちゅうしゃく
距離 きょり 空間 くうかん 場合 ばあい [ 編集 へんしゅう ] 距離 きょり 空間 くうかん M の距離 きょり 函数 かんすう d とすれば、三角 さんかく 不等式 ふとうしき
d
(
x
,
z
)
≤
d
(
x
,
y
)
+
d
(
y
,
z
)
(
∀
x
,
y
,
z
∈
M
)
{\displaystyle d(x,z)\leq d(x,y)+d(y,z)\quad (\forall x,y,z\in M)}
は距離 きょり 函数 かんすう 定義 ていぎ 要件 ようけん 一 ひと x から z までの距離 きょり x から y への距離 きょり y から z までの距離 きょり 和 わ 上 うえ 押 お
三角 さんかく 不等式 ふとうしき 距離 きょり 空間 くうかん 上 じょう 興味 きょうみ 大半 たいはん 占 し 収束 しゅうそく 性 せい 関 かか 距離 きょり 函数 かんすう 残 のこ 要件 ようけん 比較的 ひかくてき 単純 たんじゅん 例 たと 距離 きょり 空間 くうかん 任意 にんい 収束 しゅうそく 列 れつ コーシー列 れつ であるという事実 じじつ 三角 さんかく 不等式 ふとうしき 直接 ちょくせつ 帰結 きけつ xn および xm を(距離 きょり 空間 くうかん 収束 しゅうそく 定義 ていぎ 通 とお 任意 にんい ε いぷしろん 対 たい d (xn , x ) < ε いぷしろん d (xm , x ) < ε いぷしろん 三角 さんかく 不等式 ふとうしき d (xn , xm ) ≤ d (xn , x ) + d (xm , x ) < ε いぷしろん ε いぷしろん ε いぷしろん 点 てん 列 れつ {xn } は定義 ていぎ 列 れつ
ノルム空間 くうかん 誘導 ゆうどう 距離 きょり 函数 かんすう d (x , y ) ≔ ‖ x − y ‖距離 きょり 空間 くうかん x − y 始点 してん y から終点 しゅうてん x へ結 むす 解釈 かいしゃく 空間 くうかん 距離 きょり 空間 くうかん 三角 さんかく 不等式 ふとうしき 前節 ぜんせつ 述 の ノルム空間 くうかん 場合 ばあい の三角 さんかく 不等式 ふとうしき 帰着 きちゃく
逆 ぎゃく 三角 さんかく 不等式 ふとうしき [ 編集 へんしゅう ] 三角 さんかく 不等式 ふとうしき 上 うえ 評価 ひょうか 対 たい 下 した 評価 ひょうか 与 あた 逆 ぎゃく 向 む 三角 さんかく 不等式 ふとうしき reverse triangle inequality ) は三角 さんかく 不等式 ふとうしき 初等 しょとう 的 てき 帰結 きけつ 得 え 平面 へいめん 幾何 きか 言葉 ことば 言 い 三角形 さんかっけい 任意 にんい 辺 あたり 他 た 二 に 辺 へん 差 さ 大 おお 空間 くうかん 場合 ばあい
|
‖
x
‖
−
‖
y
‖
|
≤
‖
x
−
y
‖
,
{\displaystyle {\Bigl |}\|x\|-\|y\|{\Bigr |}\leq \|x-y\|,}
あるいは距離 きょり 空間 くうかん 場合 ばあい |d (y , x ) − d (x , z )| ≤ d (y , z ) ということになる。これはノルム ‖ • ‖ や距離 きょり 函数 かんすう d (x , •)リプシッツ定数 ていすう 1 のリプシッツ連続 れんぞく 函数 かんすう 示 しめ 特 とく 一様 いちよう 連続 れんぞく
逆 ぎゃく 三角 さんかく 不等式 ふとうしき 通常 つうじょう 三角 さんかく 不等式 ふとうしき 用 もち 証明 しょうめい
‖
x
‖
=
‖
(
x
−
y
)
+
y
‖
≤
‖
x
−
y
‖
+
‖
y
‖
⟹
‖
x
‖
−
‖
y
‖
≤
‖
x
−
y
‖
,
{\displaystyle \|x\|=\|(x-y)+y\|\leq \|x-y\|+\|y\|\implies \|x\|-\|y\|\leq \|x-y\|,}
‖
y
‖
=
‖
(
y
−
x
)
+
x
‖
≤
‖
y
−
x
‖
+
‖
x
‖
⟹
‖
x
‖
−
‖
y
‖
≥
−
‖
x
−
y
‖
{\displaystyle \|y\|=\|(y-x)+x\|\leq \|y-x\|+\|x\|\implies \|x\|-\|y\|\geq -\|x-y\|}
に注意 ちゅうい
−
‖
x
−
y
‖
≤
‖
x
‖
−
‖
y
‖
≤
‖
x
−
y
‖
⟹
|
‖
x
‖
−
‖
y
‖
|
≤
‖
x
−
y
‖
.
{\displaystyle -\|x-y\|\leq \|x\|-\|y\|\leq \|x-y\|\implies {\bigl |}\,\|x\|-\|y\|\,{\bigr |}\leq \|x-y\|.}
ミンコフスキー空間 くうかん 不等号 ふとうごう 反転 はんてん [ 編集 へんしゅう ] ミンコフスキー空間 くうかん において x, y がともに未 み 来光 らいこう 錐 きり 内 ない 時間 じかん 的 てき 三角 さんかく 不等式 ふとうしき 逆 ぎゃく 向 む 評価 ひょうか
‖
x
+
y
‖
≥
‖
x
‖
+
‖
y
‖
{\displaystyle \|x+y\|\geq \|x\|+\|y\|}
になる。この不等式 ふとうしき 物理 ぶつり 学 がく 的 てき 例 れい 特殊 とくしゅ 相対 そうたい 論 ろん 双子 ふたご 二 ふた 過去 かこ 光 ひかり 錐 きり 内 ない 場合 ばあい 少 すく 一方 いっぽう ヌルベクトル である場合 ばあい 同 おな 逆 ぎゃく 向 む 不等号 ふとうごう 持 も 三角 さんかく 不等式 ふとうしき 成 な 立 た 結果 けっか 任意 にんい 自然 しぜん 数 すう n に対 たい n + 1次元 じげん 成立 せいりつ
x, y がともに空間 くうかん 的 てき 場合 ばあい 通常 つうじょう 通 どお 三角 さんかく 不等式 ふとうしき 満足 まんぞく
^ z が最大 さいだい 辺 あたり 明 あき z ≤ max(x , y ) < x + y .^ 例 たと 平面 へいめん ℓ 1 マンハッタン距離 きょり )を入 い x = (1, 0)y = (0, 1)取 と 三 さん 点 てん x , y , x + y 成 な 三角形 さんかっけい 非 ひ 退化 たいか ‖ x + y ‖ = 2 = ‖ x ‖ + ‖ y ‖ を満 み
Khamsi, Mohamed A.; Kirk, William A. (2001). An introduction to metric spaces and fixed point theory ISBN 0-471-41825-0 . https://books.google.co.jp/books?id=4qXbEpAK5eUC Brock, Oliver; Trinkle, Jeff; Ramos, Fabio (2009). Robotics: Science and Systems IV ISBN 0-262-51309-9 . https://books.google.co.jp/books?id=fvCaQfBQ7qEC Ramsay, Arlan; Richtmyer, Robert D. (1995). Introduction to hyperbolic geometry ISBN 0-387-94339-0 . https://books.google.co.jp/books?id=0QA_1lKC0dwC Jacobs, Harold R. (2003). Geometry: seeing, doing, understanding ISBN 0-7167-4361-2 . https://books.google.co.jp/books?id=XhQRgZRDDq0C Stillwell, John (1997). Numbers and Geometry ISBN 978-0-387-98289-2 . https://books.google.co.jp/books?id=4elkHwVS0eUC The popular educator; fourth volume . https://books.google.co.jp/books?id=lTACAAAAQAAJ Kress, Rainer (1988). Numerical analysis ISBN 0-387-98408-9 . https://books.google.co.jp/books?id=e7ZmHRIxum0C