SierpinskiCurve

SierpinskiCurve[n]

シェルピンスキー曲線きょくせんのステップ nを表あらわす線分せんぶんを与あたえる．

詳細しょうさいとオプション

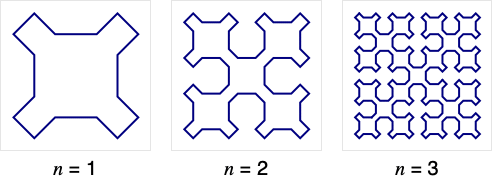
SierpinskiCurveは，シェルピンスキー(Sierpiński)空間くうかん充填じゅうてん曲線きょくせんとしても知しられている．
SierpinskiCurveは，{0,0}の周まわりの閉路へいろに相当そうとうするLineプリミティブを返かえす．

SierpinskiCurveは，座標ざひょうが占しめるであろうと考かんがえられる範囲はんいの指定していに使つかうことができるDataRangeオプションを取とる．

例題れいだい

すべて開ひらくすべて閉とじる

例れい (2)

2Dシェルピンスキー曲線きょくせん：

シェルピンスキー曲線きょくせんの近似きんじの長ながさ：

式しきは以下いかのようになる：

2Dのシェルピンスキー曲線きょくせんをスプライン曲線きょくせんで可視かし化かする：

スコープ (6)標準的な使用例のスコープの概要

曲線きょくせん指定してい (2)

2Dシェルピンスキー曲線きょくせん：

シェルピンスキー曲線きょくせんの番ばん目めの近似きんじ：

曲線きょくせんのスタイル (4)

太ふとさの異ことなるシェルピンスキー曲線きょくせん：

スケールされたサイズによる太ふとさ：

印刷いんさつ用ようポイント数すうによる太ふとさ：

破線はせん曲線きょくせん：

色いろ付つきの曲線きょくせん：

オプション (1)各オプションの一般的な値と機能

DataRange (1)

DataRangeを使つかうと生成せいせいするメッシュ座標ざひょうの範囲はんいを指定していすることができる：

別べつの範囲はんいを指定していする：

アプリケーション (4)この関数で解くことのできる問題の例

SierpinskiCurveは，線分せんぶんを直線ちょくせんで結むすばれた曲線きょくせんに繰くり返かえし変換へんかんすることで作成さくせいされる：

次つぎの反復はんぷく：

2Dのシェルピンスキー曲線きょくせんを可視かし化かする：

スプライン曲線きょくせんを使つかう：

多角たかく形がたを構築こうちくする：

シェルピンスキー曲線きょくせんのテクスチャを曲面きょくめんに適用てきようする：

特性とくせいと関係かんけい (3)

SierpinskiCurveは直線ちょくせんからなる：

2Dシェルピンスキー曲線きょくせんの周しゅう長ちょうを求もとめる：

DataRangerange はRescalingTransform[{…},range]を使つかうことに等ひとしい：

RescalingTransformを使つかう：

考かんがえられる問題もんだい (2)

デフォルトで，シェルピンスキー曲線きょくせんの座標ざひょうは単位たんい正方形せいほうけい内ないにはない：

DataRangeを使つかって正方形せいほうけい内ないにシェルピンスキー曲線きょくせんを生成せいせいする：

SierpinskiCurveは大おおきすぎて生成せいせいできないことがある：

おもしろい例題れいだい (1)

走査そうさアニメーション：

トップへ

その他たのラーニングリソース

テクニカルサポート

Wolframソリューション

教育きょういくのためのWolframソリューション

使つかい始はじめる

Grow Your Skills

Wolframと繋つながる

大人おとな用ようの教育きょういくプログラム

若者わかもののための教育きょういくプログラム

読よむ

SierpinskiCurve

詳細しょうさいとオプション

例題れいだい

例れい (2)