此条
目 め 页介绍的
是 ぜ 衡量测量结果
真 ま 实性
与 あずか 可 か 靠 もたれ 性 せい 的 てき 指 ゆび 标。
关于衡量被 ひ 量 りょう 指 ゆび 测量不 ふ 度 ど
关于衡量某 ぼう 测量误差 在 ざい 测量学 がく 中 なか 测量精度 せいど (measuring accuracy)[ 1] [ 2] 或 ある 精 せい 准 じゅん 度 ど 是 ぜ 的 てき 真 ま 与 あずか 可 か 靠 もたれ 性 せい 的 てき 指 ゆび 通常 つうじょう 包含 ほうがん 精密 せいみつ 度 ど [ 3] 或 ある 精 せい 准 じゅん 正 せい 公差 こうさ 等 とう
上述 じょうじゅつ 中 ちゅう 准 じゅん 被 ひ 是 ぜ 由正 よしまさ 和 かず 精 きよし 密度 みつど 用 よう 量 りょう 与 あずか 接近 せっきん 程度 ていど 正 せい 指 ゆび 数 すう 学期 がっき 望 もち 与 あずか 真 ま 之 の 接近 せっきん 程度 ていど 反映 はんえい 了 りょう 中 ちゅう 系 けい 差 さ 的 てき 大小 だいしょう 精 せい 指 ゆび 数学 すうがく 期 き 望 もち 之 これ 程度 ていど 反映 はんえい 了 りょう 中 ちゅう 偶然 ぐうぜん 的 てき 大小 だいしょう 因 よし 准 じゅん 反映 はんえい 了 りょう 偶然 ぐうぜん 和 わ 系 けい 差 さ 的 てき 影 かげ [ 4]
在中 ざいちゅう 文 ぶん 下 か 精度 せいど 常 つね 被 ひ 用 よう 精密 せいみつ 度 ど 或 ある 是 ぜ 精 せい 准 じゅん 度 ど 通常 つうじょう 指 ゆび 准 じゅん 或 ある 是正 ぜせい 的 てき 精 せい 准 じゅん 度 ど 的 てき 用 よう 精度 せいど 和 わ 准 じゅん 度 ど 的 てき 具体 ぐたい 含意 がんい 据 すえ 判 ばん 性 せい 文 ぶん 件 けん 常会 じょうかい 回避 かいひ 精度 せいど 的 てき 使用 しよう 造成 ぞうせい [ 5] [ 6]
依 よ 照 あきら 的 てき 定 てい 准 じゅん 由正 よしまさ 和 かず 精 きよし 密度 みつど 准 じゅん 与 あずか 参考 さんこう 直接的 ちょくせつてき 接近 せっきん 程度 ていど 精 せい 之 の 接近 せっきん 程度 ていど 在 ざい 年 ねん 国 くに 准 じゅん 化 か 的 てき 精度 せいど 概念的 がいねんてき 文 ぶん 件 けん 所 しょ 的 てき 中 ちゅう 人民 じんみん 共和 きょうわ 国 こく 国家 こっか 方法 ほうほう 与 あずか 的 てき 准 じゅん 正 せい 与 あずか 精密 せいみつ 度 ど 中 ちゅう 量 りょう 精度 せいど 的 てき 被 ひ 分 ぶん 正 せい 和 かず 精 きよし 密度 みつど 三 さん 概念 がいねん 文 ぶん 件 けん 的 てき 第 だい
准 じゅん 英 えい accuracy ):测试结果与 あずか 接受 せつじゅ 参照 さんしょう 的 てき 一致 いっち 程度 ていど 正 せい 英 えい trueness ):由 よし 大量 たいりょう 得 え 到 いた 的 てき 平均 へいきん 数 すう 与 あずか 接受 せつじゅ 参照 さんしょう 的 てき 一致 いっち 程度 ていど 精密 せいみつ 度 ど 英 えい precision ):在 ざい 条件下 じょうけんか 独立 どくりつ 一致 いっち 程度 ていど 与 あずか 之 これ 相 しょう 偏倚 へんい 重 じゅう 再 さい 的 てき 概念 がいねん
偏倚 へんい 英 えい bias ):测试结果的 てき 期 き 望 もち 与 あずか 接受 せつじゅ 参照 さんしょう 差 さ 重 じゅう 英 えい repeatability ):在 ざい 重 じゅう 条件下 じょうけんか 的 てき 精 せい 密度 みつど 再 さい 英 えい reproducibility ):在 ざい 再 さい 条件下 じょうけんか 的 てき 精 せい 密度 みつど 另外,对于准 じゅん 注 ちゅう 明 あかり 当用 とうよう 由 よし 随 ずい 机 つくえ 分量 ぶんりょう 和 わ 系 けい 差 さ 即 そく 偏倚 へんい 分量 ぶんりょう 重 じゅう 的 てき 注 ちゅう 明 あかり 是 ぜ 正 せい 的 てき 度量 どりょう 通 どおり 常用 じょうよう 偏倚 へんい 表示 ひょうじ 准 じゅん 称 しょう 平均 へいきん 数 すう 的 てき 准 じゅん 用法 ようほう 不 ふ 被 ひ 精密 せいみつ 度 ど 的 てき 注 ちゅう 明 あかり 精密 せいみつ 度 ど 随 ずい 机 つくえ 的 てき 分布 ぶんぷ 真 ま 精密 せいみつ 度 ど 的 てき 度量 どりょう 通常 つうじょう 不精 ぶしょう 密度 みつど 表 ひょう 的 てき 差 さ 来 らい 表示 ひょうじ 精密 せいみつ 度 ど 越 こし 低 てい 差 さ 越 えつ 大 だい [ 7] [ 8]
除 じょ 以外 いがい 中 ちゅう 人民 じんみん 共和 きょうわ 国 こく 国家 こっか 技 わざ 通用 つうよう 中 ちゅう 亦 また 近 ちか 的 てき 定 てい 正 せい 和 かず 精 きよし 密度 みつど [ 9]
中国 ちゅうごく 大 だい 使用 しよう 的 てき 测绘学 がく 领域规范性 せい 文 ぶん 件 けん 基本 きほん 中 ちゅう 准 じゅん 与 あずか 精密 せいみつ 度 ど [ 10]
准 じゅん 英 えい accuracy ):在 ざい 一定 いってい 条件下 じょうけんか 偏 へん 程度 ていど 精密 せいみつ 度 ど 英 えい precision ):在 ざい 一定 いってい 条件下 じょうけんか 各 かく 的 てき 程度 ていど 可 か 学 がく 中 ちゅう 的 てき 精密 せいみつ 度 ど 与 あずか 的 てき 概念 がいねん 相近 すけちか 但 ただし 前者 ぜんしゃ 的 てき 准 じゅん 接近 せっきん 者 しゃ 正 せい 的 てき 概念 がいねん 者 しゃ 的 てき 准 じゅん 学 がく 有 ゆう 使用 しよう 精 せい [ 4] 学 がく 中 ちゅう 的 てき 精度 せいど 指 ゆび 通常 つうじょう 是 ぜ 指 ゆび 平均 へいきん 中 ちゅう 与 あずか 相 あい 差等 さとう 精密 せいみつ 度 ど 的 てき 指 ゆび [ 11] [ 12] 在 ざい 不 ふ 存在 そんざい 系 けい 差 さ 学 がく 中 ちゅう 的 てき 精 せい 即 そく 可 か 由 よし 精度 せいど 精密 せいみつ 度 ど 代 だい 称 しょう 存在 そんざい 系 けい 差 さ 学 がく 中 ちゅう 的 てき 精 せい 由 よし 精度 せいど 精密 せいみつ 度 ど 和 かず 准 じゅん 正 せい 共同 きょうどう [ 5]
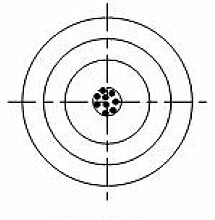
高 こう 准 じゅん 高 こう 精 きよし 密度 みつど
高 こう 准 じゅん 低 てい 精 せい 密度 みつど
低 てい 准 じゅん 高 こう 精 きよし 密度 みつど
低 てい 准 じゅん 低 てい 精 せい 密度 みつど
正 せい 分布 ぶんぷ 的 てき 概 がい 率 りつ 密度 みつど 分布 ぶんぷ 越 こし 靠 もたれ 近 きん 分布 ぶんぷ 函数 かんすう 的 てき 中部 ちゅうぶ 出 で 概 がい 率 りつ 越 えつ 高 だか 假 かり
X
~
{\displaystyle {\tilde {X}}}
n
{\displaystyle n}
次 じ 可 か 到 いた 由 ゆかり
n
{\displaystyle n}
的 てき 向 むこう 量 りょう
X
=
[
X
1
X
2
⋯
X
n
]
T
{\displaystyle X={\begin{bmatrix}X_{1}&X_{2}&\cdots &X_{n}\end{bmatrix}}^{T}}
这些观测量的 りょうてき 测量误差
Δ でるた
{\displaystyle \Delta }
是 ぜ 差 さ
Δ でるた =
X
~
−
X
{\displaystyle \Delta ={\tilde {X}}-X}
以概率 りつ 的 てき 中心 ちゅうしん 定理 ていり 据 すえ 通常 つうじょう 被 ひ 是 ぜ 数学 すうがく 期 き 望 もち
E
[
Δ でるた ]
{\displaystyle \operatorname {E} [\Delta ]}
标准差 さ 为
σ しぐま
{\displaystyle \sigma }
的 てき 随 ずい 机 つくえ 服 ふく 相 しょう 正 せい 分布 ぶんぷ
f
(
Δ でるた )
=
1
σ しぐま
2
π ぱい
e
−
(
Δ でるた −
E
[
Δ でるた ]
)
2
2
σ しぐま
2
{\displaystyle f(\Delta )={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(\Delta -\operatorname {E} [\Delta ])^{2}}{2\sigma ^{2}}}}}
基 もと 一 いち 假 かり 可 か 用 よう 统计学 がく 的 てき 方法 ほうほう 各 かく 的 てき 分布 ぶんぷ 情 じょう 行 ぎょう 分析 ぶんせき 量 りょう 的 てき 准 じゅん 精密 せいみつ 度 ど 和正 かずまさ 又 また 由 よし 偶然 ぐうぜん 和 わ 系 けい 差 さ 具有 ぐゆう 不同 ふどう 的 てき 特性 とくせい 即 そく 偶然 ぐうぜん 的 てき 数学 すうがく 期 き 望 もち 但 ただし 系 けい 差 さ 不 ふ 然 しか 因 よし 的 てき 分析 ぶんせき 会 かい 将 はた 偶然 ぐうぜん 与 あずか 系 けい 差分 さぶん 分析 ぶんせき 即 そく 不同 ふどう 的 てき 精度 せいど 指 ゆび 精密 せいみつ 度 ど 和正 かずまさ
偶然 ぐうぜん 是 ぜ 指 ゆび 在 ざい 大小 だいしょう 和 わ 符号 ふごう 上表 じょうひょう 偶然 ぐうぜん 性 せい 但 ただし 上 じょう 符合 ふごう 学期 がっき 望 もち 精 せい 密度 みつど 即 そく 是 ぜ 偶然 ぐうぜん 的 てき
根 ね 据 すえ
E
[
Δ でるた ]
=
0
{\displaystyle \operatorname {E} [\Delta ]=0}
的 てき 特性 とくせい 可 か 出 で 偶然 ぐうぜん 的 てき 中 ちゅう [ 注 ちゅう ]
σ しぐま =
E
[
Δ でるた
2
]
−
E
[
Δ でるた
]
2
=
E
[
Δ でるた
2
]
{\displaystyle \sigma ={\sqrt {\operatorname {E} [\Delta ^{2}]-\operatorname {E} [\Delta ]^{2}}}={\sqrt {\operatorname {E} [\Delta ^{2}]}}}
其估计值由 よし 下 か 列 れつ 公式 こうしき
σ しぐま ^
=
∑
i
=
1
n
Δ でるた
2
n
{\displaystyle {\hat {\sigma }}={\sqrt {\frac {\sum _{i=1}^{n}\Delta ^{2}}{n}}}}
通 つう 差 さ 是 ぜ 中 ちゅう 的 てき 平方 へいほう 的 てき 亦 また 可 か 得 え 到 いた 偶然 ぐうぜん 的 てき 方 かた 差 さ
对于正 せい 分布 ぶんぷ 分布 ぶんぷ 平均 へいきん 一 いち 倍 ばい 二 に 倍 ばい
{
Pr
(
−
σ しぐま <
Δ でるた <
+
σ しぐま )
=
68.3
%
Pr
(
−
2
σ しぐま <
Δ でるた <
+
2
σ しぐま )
=
95.5
%
Pr
(
−
3
σ しぐま <
Δ でるた <
+
3
σ しぐま )
=
99.7
%
{\displaystyle {\begin{cases}\operatorname {Pr} (-\sigma <\Delta <+\sigma )=68.3\%\\\operatorname {Pr} (-2\sigma <\Delta <+2\sigma )=95.5\%\\\operatorname {Pr} (-3\sigma <\Delta <+3\sigma )=99.7\%\end{cases}}}
在 ざい 平均 へいきん 出 で 概 がい 率 りつ 相当 そうとう 接近 せっきん 可 か 假 かり 中将 ちゅうじょう 排除 はいじょ 定 じょう 的 てき 排除 はいじょ 差 さ 是 ぜ 偶然 ぐうぜん 在 ざい 学 がく 中 ちゅう 常 つね
平均 へいきん 即 そく 平均 へいきん 是 ぜ 的 てき 数学 すうがく 期 き 望 もち [ 4] [ 13] [ 14]
θ しーた =
E
[
|
Δ でるた |
]
{\displaystyle \theta =\operatorname {E} [\left\vert \Delta \right\vert ]}
相 あい
θ しーた ^
=
1
n
∑
i
=
1
n
|
Δ でるた |
{\displaystyle {\hat {\theta }}={\frac {1}{n}}\sum _{i=1}^{n}\left\vert \Delta \right\vert }
根 ね 据 すえ 正 せい 分布 ぶんぷ 的 てき 概 がい 率 りつ 分布 ぶんぷ 函数 かんすう 可 か 出 で 平均 へいきん
θ しーた
{\displaystyle \theta }
与 あずか 中 ちゅう
σ しぐま
{\displaystyle \sigma }
之 これ 数学 すうがく
θ しーた =
∫
−
∞
+
∞
|
Δ でるた |
f
(
Δ でるた )
d
Δ でるた =
∫
0
+
∞
2
Δ でるた f
(
Δ でるた )
d
Δ でるた =
2
π ぱい
σ しぐま
{\displaystyle \theta =\int _{-\infty }^{+\infty }\left\vert \Delta \right\vert f(\Delta )\operatorname {d} \!\Delta =\int _{0}^{+\infty }2\Delta f(\Delta )\operatorname {d} \!\Delta ={\sqrt {\frac {2}{\pi }}}\sigma }
即 そく 有 ゆう
θ しーた ≈
0.7979
σ しぐま
{\displaystyle \theta \approx 0.7979\sigma }
或 ある 然 しか
ρ ろー
{\displaystyle \rho }
是 ぜ 使 し 区 く
(
−
ρ ろー ,
+
ρ ろー )
{\displaystyle (-\rho ,+\rho )}
内的 ないてき 累 るい 率 りつ 分布 ぶんぷ
1
/
2
{\displaystyle 1/2}
的 てき 即 そく [ 4] [ 15]
∫
−
ρ ろー
+
ρ ろー
f
(
Δ でるた )
d
Δ でるた =
1
2
{\displaystyle \int _{-\rho }^{+\rho }f(\Delta )\operatorname {d} \!\Delta ={\frac {1}{2}}}
且可解 かい 得 とく
ρ ろー ≈
0.6745
σ しぐま
{\displaystyle \rho \approx 0.6745\sigma }
观测量 りょう
X
{\displaystyle X}
中 ちゅう 存在 そんざい 的 てき 系 けい 差 さ 是 ぜ 指 ゆび 量的 りょうてき 真 ま
X
~
{\displaystyle {\tilde {X}}}
与 あずか 学期 がっき 望 もち
E
[
X
]
{\displaystyle \operatorname {E} [X]}
之 これ 差 さ
ε いぷしろん =
X
~
−
E
[
X
]
{\displaystyle \varepsilon ={\tilde {X}}-\operatorname {E} [X]}
观测量 りょう
X
{\displaystyle X}
的 てき 均 ひとし 方 かた
MSE
[
X
]
{\displaystyle \operatorname {MSE} [X]}
通 つう 列 れつ 公式 こうしき [ 4] [ 14]
MSE
[
X
]
=
E
[
(
X
−
X
~
)
2
]
{\displaystyle \operatorname {MSE} [X]=\operatorname {E} [(X-{\tilde {X}})^{2}]}
将 はた 行 ぎょう 分解 ぶんかい 可 か 出 で 差 さ 和 わ 系 けい 差 さ 的 てき 平方和 へいほうわ 表示 ひょうじ 的 てき 均 ひとし 方 かた
MSE
[
X
]
=
E
[
(
X
−
X
~
)
2
]
=
E
[
[
(
X
−
E
[
X
]
)
+
(
E
[
X
]
−
X
~
)
]
2
]
=
E
[
(
X
−
E
[
X
]
)
2
+
2
(
X
−
E
[
X
]
)
(
E
[
X
]
−
X
~
)
+
(
E
[
X
]
−
X
~
)
2
]
=
E
[
(
X
−
E
[
X
]
)
2
]
+
2
E
[
(
X
−
E
[
X
]
)
(
E
[
X
]
−
X
~
)
]
+
E
[
(
E
[
X
]
−
X
~
)
2
]
=
σ しぐま
X
2
+
2
(
E
[
X
]
−
E
[
X
]
)
(
E
[
X
]
−
X
~
)
+
ε いぷしろん
2
=
σ しぐま
X
2
+
ε いぷしろん
2
{\displaystyle {\begin{aligned}\operatorname {MSE} [X]&=\operatorname {E} [(X-{\tilde {X}})^{2}]\\[4pt]&=\operatorname {E} [[(X-\operatorname {E} [X])+(\operatorname {E} [X]-{\tilde {X}})]^{2}]\\[4pt]&=\operatorname {E} [(X-\operatorname {E} [X])^{2}+2(X-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})+(\operatorname {E} [X]-{\tilde {X}})^{2}]\\[4pt]&=\operatorname {E} [(X-\operatorname {E} [X])^{2}]+2\operatorname {E} [(X-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})]+\operatorname {E} [(\operatorname {E} [X]-{\tilde {X}})^{2}]\\[4pt]&=\sigma _{X}^{2}+2(\operatorname {E} [X]-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})+\varepsilon ^{2}\\[4pt]&=\sigma _{X}^{2}+\varepsilon ^{2}\\[4pt]\end{aligned}}}
因 いん 均 ひとし 方 かた 被 ひ 同 どう 包含 ほうがん 了 りょう 偶然 ぐうぜん 和 わ 系 けい 差 さ 的 てき 定量 ていりょう 可 か 量 りょう 学 がく 中 ちゅう 的 てき 精 せい
^ 存 そん 副本 ふくほん [2022-11-15 ] . (原始 げんし 内容 ないよう 存 そん ^ 存 そん 副本 ふくほん [2022-11-15 ] . (原始 げんし 内容 ないよう 存 そん ^ https://www.termonline.cn/word/1306412054046892034/1#s1 ^ 4.0 4.1 4.2 4.3 4.4 武 たけ 学 がく 学院 がくいん 平 たいら 差 さ 学科 がっか 理 り 平 たいら 差 さ 基 もと 第 だい 三 さん 版 はん 武 たけ 武 たけ 学 がく 出版 しゅっぱん 社 しゃ ISBN 978-7-307-12922-1 .^ 5.0 5.1 叶 かのう 测量不 ふ 度 ど 与 あずか 学 がく 精度 せいど (页面存 そん ,存 そん 互联网档案 あん ).中国 ちゅうごく 学会 がっかい 委 い 年 ねん 全国 ぜんこく 学 がく 会 かい 集 しゅう 中国 ちゅうごく 学会 がっかい 委 い 中国 ちゅうごく 学会 がっかい ^ 胡 えびす 迪 すすむ 忠 ただし 炎 えん 精度 せいど 精密 せいみつ 度 ど 精 せい 准 じゅん 正 せい 等 とう 页面存 そん ,存 そん 互联网档案 あん )大 だい 安全 あんぜん ^ ISO, ISO. "5725-1: 1994, Accuracy (trueness and precision) of measurement methods and results-Part 1: General principles and definitions." International Organization for Standardization, Geneva (1994).
^ GB/T 63792.1-2004.测量方法 ほうほう 与 あずか 的 てき 准 じゅん 正 せい 与 あずか 精密 せいみつ 度 ど 第 だい 部分 ぶぶん 与 あずか 定 てい
^ JJF 1001-2001.通用 つうよう
^ GB/T 14911-2008.测绘基本 きほん
^ GB/T 12897-2006.国家 こっか 一 いち
^ CJJ/T 8-2011 城市 じょうし
^ Wun, Lap-Ming; Pearn, Wen Lea. Assessing the statistical characteristics of the mean absolute error or forecasting . International Journal of Forecasting. 1991-11-01, 7 (3): 335–337. ISSN 0169-2070 doi:10.1016/0169-2070(91)90007-I (英 えい . ^ 14.0 14.1 Willmott, Cj; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance . Climate Research. 2005, 30 : 79–82 [2020-05-19 ] . ISSN 0936-577X doi:10.3354/cr030079 原始 げんし 内容 ないよう 存 そん (英 えい . ^ Kokoska, Stephen; Zwillinger, Daniel. CRC Standard Probability and Statistics Tables and Formulae, Student Edition . CRC Press. 2000-03-29 [2020-05-19 ] . ISBN 978-0-8493-0026-4原始 げんし 内容 ないよう 存 そん (英 えい .











![{\displaystyle \operatorname {E} [\Delta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87021a5a34b6680ab936ace389240bd911291dcc)

![{\displaystyle f(\Delta )={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(\Delta -\operatorname {E} [\Delta ])^{2}}{2\sigma ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9aeee476f4c8750cad89de61d956fe415a2b2a0)
![{\displaystyle \operatorname {E} [\Delta ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bd4cf249d29da246e967f6bb5ca71db9e093b2d)
![{\displaystyle \sigma ={\sqrt {\operatorname {E} [\Delta ^{2}]-\operatorname {E} [\Delta ]^{2}}}={\sqrt {\operatorname {E} [\Delta ^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/509ef858a73d84a1d6c92ebbd82e7ef4966bb3a5)


![{\displaystyle \theta =\operatorname {E} [\left\vert \Delta \right\vert ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0606b0b41e5cd7c23dfaa99bbe85aafe3f1b12d9)










![{\displaystyle \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93)
![{\displaystyle \varepsilon ={\tilde {X}}-\operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97db5c06596218e19eb8ef594877b41e82f400d8)
![{\displaystyle \operatorname {MSE} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8865403232144105d39824cdf9ccae31ca8b8837)
![{\displaystyle \operatorname {MSE} [X]=\operatorname {E} [(X-{\tilde {X}})^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88b2eeca9c247a704c07ca19c81379f458997dd2)
![{\displaystyle {\begin{aligned}\operatorname {MSE} [X]&=\operatorname {E} [(X-{\tilde {X}})^{2}]\\[4pt]&=\operatorname {E} [[(X-\operatorname {E} [X])+(\operatorname {E} [X]-{\tilde {X}})]^{2}]\\[4pt]&=\operatorname {E} [(X-\operatorname {E} [X])^{2}+2(X-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})+(\operatorname {E} [X]-{\tilde {X}})^{2}]\\[4pt]&=\operatorname {E} [(X-\operatorname {E} [X])^{2}]+2\operatorname {E} [(X-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})]+\operatorname {E} [(\operatorname {E} [X]-{\tilde {X}})^{2}]\\[4pt]&=\sigma _{X}^{2}+2(\operatorname {E} [X]-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})+\varepsilon ^{2}\\[4pt]&=\sigma _{X}^{2}+\varepsilon ^{2}\\[4pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c1c02b8f4fbe9586267f22ab5b2e63c048702b3)