একক বৃত্ত


গণিতে, একক বৃত্ত হলো একটি একক ব্যাসার্ধ বিশিষ্ট বৃত্ত—অর্থাৎ, যার ব্যাসার্ধ ১ একক।[১] প্রায়শই, বিশেষত ত্রিকোণমিতির ক্ষেত্রে, একক বৃত্তটি ইউক্লিডীয় সমতলে কার্তেসীয় স্থানাঙ্ক ব্যবস্থায় (0, 0) কেন্দ্রবিশিষ্ট একটি বৃত্ত যার ব্যাসার্ধ ১ একক। টপোলজিতে, এটিকে প্রায়শই S1 হিসাবে উল্লেখ করা হয়, কারণ এটি একটি একমাত্রিক একক n-গোলক।[২][note ১]
যদি, (x, y) একক বৃত্তের পরিধির উপরস্থ একটি বিন্দু হয় , তবে |x| এবং |y| সমকোণী ত্রিভুজের দুইটি বাহু হয়, যার অতিভুজের দৈর্ঘ্য ১ একক।এইভাবে, পিথাগোরাসের উপপাদ্য অনুসারে, x এবং y নিম্নোক্ত সমীকরণটিকে সিদ্ধ করে:
যেহেতু, সকল x এর জন্য x2 = (−x)2 , এবং যেহেতু একক বৃত্তের উপর অবস্থিত x- অথবা y অক্ষের সাপেক্ষে যেকোনো বিন্দুর প্রতিবিম্ব একক বৃত্তের উপর অবস্থিত (শুধুমাত্র প্রথম চতুর্ভাগের জন্য নয়), বৃত্তের উপর অবস্থিত সকল (x, y) বিন্দুর জন্য উপর্যুক্ত সমীকরণটি কাজ করে।
একক বৃত্তের অভ্যন্তরীণকে বলা হয় মুক্ত একক চাকতি, যেখানে একক বৃত্তের অভ্যন্তরীণ অংশ এবং একক বৃত্তসহ একত্রে একে বদ্ধ একক চাকতি বলা হয়।
একজন অন্যান্য একক বৃত্তসমূহকে সংজ্ঞায়িত করতে দূরত্বের অন্যান্য ধারণাও ব্যবহার করতে পারেন। উদাহরণস্বরূপ: র্যামেনিয়ান বৃত্ত; অতিরিক্ত উদাহরণের জন্য গাণিতিক নর্ম্ নিবন্ধনটি দেখতে পারেন।
জটিল সমতলীয় ব্যবস্থায়
[সম্পাদনা]একক বৃত্তকে একক জটিল সংখ্যা হিসেবে বিবেচনা করা যেতে পারে , i.e., জটিল সংখ্যাসমূহের সেট z যার রূপ হয়ে থাকে।
সকল t এর জন্য(আরও দেখুন : সিস)। এই সম্পর্কটি অয়লারের সূত্রকে প্রকাশ করে। কোয়ান্টাম বলবিজ্ঞানে, এটি দশা উৎপাদককে নির্দেশ কর।

একক বৃত্তে ত্রিকোণমিতিক ফাংশন
[সম্পাদনা]
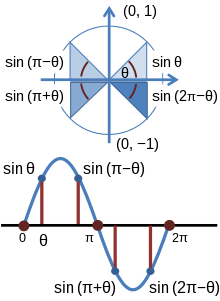
একক বৃত্তের উপর
x2 + y2 = 1 সমীকরণ থেকে নিম্নোক্ত সম্পর্কটি পাওয়া যায়
একক বৃত্ত থেকে আরও দেখা যায় যে sine এবং cosine মূলত পর্যায়বৃত্ত ফাংশন , যা নিম্নোক্ত অভেদকসমূহ সিদ্ধ করে:
যেকোনো পূর্ণসংখ্যা k এর জন্য।
একক বৃত্ত ব্যবহার করে, নিম্নে লেবেলযুক্ত কোণসমূহ ছাড়াও অন্য যেকোন কোণের জন্য ত্রিকোণমিতিক ফাংশনের মানগুলি কোণ যোগফল এবং পার্থক্য সূত্রগুলি ব্যবহার করে ক্যালকুলেটর ব্যবহার না করেও গণনা করা যেতে পারে।

জটিল গতিবিদ্যা
[সম্পাদনা]
বিবর্তন ফাংশনের সঙ্গে বিচ্ছিন্ন অরৈখিক গতিশীল সিস্টেমের জুলিয়া সেট:
একটি একক বৃত্ত। এটি সবচেয়ে সহজতম একটি কেস, তাই এটি গতিশীল সিস্টেমের গবেষণায় ব্যাপকভাবে ব্যবহৃত হয়।
মন্তব্য
[সম্পাদনা]- ↑ Confusingly, in geometry a unit circle is often considered to be a 2-sphere—not a 1-sphere. The unit circle is "embedded" in a 2-dimensional plane that contains both height and width—hence why it is called a 2-sphere in geometry. However, the surface of the circle itself is one-dimensional, which is why topologists classify it as a 1-sphere. For further discussion, see the technical distinction between a circle and a disk.[২]
তথ্যসূত্র
[সম্পাদনা]
- ↑ Weisstein, Eric W.। "Unit Circle"। mathworld.wolfram.com (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০২০-০৫-০৫।
- ↑ ক খ Weisstein, Eric W.। "Hypersphere"। mathworld.wolfram.com (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০২০-০৫-০৬।







