Pi
| Part of a series of articles on the |
| mathematical constant |
|---|
 |
| 3.1415926535897932384626433... |
| Uses |
| Properties |
| Value |
| People |
| History |
| In culture |
| Related topics |
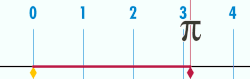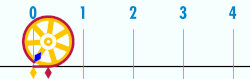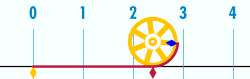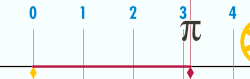
The number
The number
For thousands of years, mathematicians have attempted to extend their understanding of
Because it relates to a circle,
Fundamentals
Name
The symbol used by mathematicians to represent the ratio of a circle's circumference to its diameter is the lowercase Greek letter
The choice of the symbol
Definition

The ratio is constant, regardless of the circle's size. For example, if a circle has twice the diameter of another circle, it will also have twice the circumference, preserving the ratio . This definition of
Here, the circumference of a circle is the arc length around the perimeter of the circle, a quantity which can be formally defined independently of geometry using limits—a concept in calculus.[4] For example, one may directly compute the arc length of the top half of the unit circle, given in Cartesian coordinates by the equation , as the integral:[5]
An integral such as this was proposed as a definition of
Integration is no longer commonly used in a first analytical definition because, as Remmert 2012 explains, differential calculus typically precedes integral calculus in the university curriculum, so it is desirable to have a definition of
In a similar spirit,
and there is a unique positive real number
A variation on the same idea, making use of sophisticated mathematical concepts of topology and algebra, is the following theorem:[12] there is a unique (up to automorphism) continuous isomorphism from the group R/Z of real numbers under addition modulo integers (the circle group), onto the multiplicative group of complex numbers of absolute value one. The number
Irrationality and normality
The digits of
Since the advent of computers, a large number of digits of
Transcendence
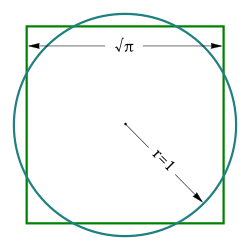
In addition to being irrational,
The transcendence of
An unsolved problem thus far is the question of whether or not the numbers
Continued fractions
As an irrational number,
Truncating the continued fraction at any point yields a rational approximation for
Approximate value and digits
Some approximations of pi include:
- Integers: 3
- Fractions: Approximate fractions include (in order of increasing accuracy) 22/7, 333/106, 355/113, 52163/16604, 103993/33102, 104348/33215, and 245850922/78256779.[25] (List is selected terms from OEIS: A063674 and OEIS: A063673.)
- Digits: The first 50 decimal digits are 3.14159265358979323846264338327950288419716939937510...[29] (see OEIS: A000796)
Digits in other number systems
- The first 48 binary (base 2) digits (called bits) are 11.001001000011111101101010100010001000010110100011... (see OEIS: A004601)
- The first 36 digits in ternary (base 3) are 10.010211012222010211002111110221222220... (see OEIS: A004602)
- The first 20 digits in hexadecimal (base 16) are 3.243F6A8885A308D31319...[30] (see OEIS: A062964)
- The first five sexagesimal (base 60) digits are 3;8,29,44,0,47[31] (see OEIS: A060707)
Complex numbers and Euler's identity
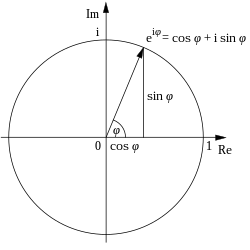
Any complex number, say z, can be expressed using a pair of real numbers. In the polar coordinate system, one number (radius or r) is used to represent z's distance from the origin of the complex plane, and the other (angle or
where i is the imaginary unit satisfying . The frequent appearance of
where the constant e is the base of the natural logarithm. This formula establishes a correspondence between imaginary powers of e and points on the unit circle centred at the origin of the complex plane. Setting in Euler's formula results in Euler's identity, celebrated in mathematics due to it containing five important mathematical constants:[33][34]
There are n different complex numbers z satisfying , and these are called the "n-th roots of unity"[35] and are given by the formula:
History
Surviving approximations of
Polygon approximation era


The first recorded algorithm for rigorously calculating the value of
In ancient China, values for
The Indian astronomer Aryabhata used a value of 3.1416 in his Āryabhaṭīya (499 AD).[50] Around 1220, Fibonacci computed 3.1418 using a polygonal method devised independently of Archimedes.[51] Italian author Dante apparently employed the value .[51]
The Persian astronomer Jamshīd al-Kāshī produced nine sexagesimal digits, roughly the equivalent of 16 decimal digits, in 1424, using a polygon with sides,[52] which stood as the world record for about 180 years.[53] French mathematician François Viète in 1579 achieved nine digits with a polygon of sides.[53] Flemish mathematician Adriaan van Roomen arrived at 15 decimal places in 1593.[53] In 1596, Dutch mathematician Ludolph van Ceulen reached 20 digits, a record he later increased to 35 digits (as a result,
Infinite series

The calculation of
In 1593, François Viète published what is now known as Viète's formula, an infinite product (rather than an infinite sum, which is more typically used in
In 1655, John Wallis published what is now known as Wallis product, also an infinite product:[65]

In the 1660s, the English scientist Isaac Newton and German mathematician Gottfried Wilhelm Leibniz discovered calculus, which led to the development of many infinite series for approximating
In 1671, James Gregory, and independently, Leibniz in 1673, discovered the Taylor series expansion for arctangent:[59][67][68]
This series, sometimes called the Gregory–Leibniz series, equals when evaluated with .[68] But for , it converges impractically slowly (that is, approaches the answer very gradually), taking about ten times as many terms to calculate each additional digit.[69]
In 1699, English mathematician Abraham Sharp used the Gregory–Leibniz series for to compute
In 1706, John Machin used the Gregory–Leibniz series to produce an algorithm that converged much faster:[71][72][73]
Machin reached 100 digits of
Isaac Newton accelerated the convergence of the Gregory–Leibniz series in 1684 (in an unpublished work; others independently discovered the result):[76]
Leonhard Euler popularized this series in his 1755 differential calculus textbook, and later used it with Machin-like formulae, including with which he computed 20 digits of
Machin-like formulae remained the best-known method for calculating
In 1844, a record was set by Zacharias Dase, who employed a Machin-like formula to calculate 200 decimals of
In 1853, British mathematician William Shanks calculated
Rate of convergence
Some infinite series for
As individual terms of this infinite series are added to the sum, the total gradually gets closer to
An infinite series for
The following table compares the convergence rates of these two series:
| Infinite series for |
After 1st term | After 2nd term | After 3rd term | After 4th term | After 5th term | Converges to: |
|---|---|---|---|---|---|---|
| 4.0000 | 2.6666 ... | 3.4666 ... | 2.8952 ... | 3.3396 ... | ||
| 3.0000 | 3.1666 ... | 3.1333 ... | 3.1452 ... | 3.1396 ... |
After five terms, the sum of the Gregory–Leibniz series is within 0.2 of the correct value of
Irrationality and transcendence
Not all mathematical advances relating to
Swiss scientist Johann Heinrich Lambert in 1768 proved that
Adoption of the symbol π
The first recorded use of the symbol
The earliest known use of the Greek letter
Euler started using the single-letter form beginning with his 1727 Essay Explaining the Properties of Air, though he used
Modern quest for more digits
Motives for computing π

For most numerical calculations involving
Computer era and iterative algorithms
The development of computers in the mid-20th century again revolutionized the hunt for digits of
Two additional developments around 1980 once again accelerated the ability to compute
The Gauss–Legendre iterative algorithm:
Initialize Iterate Then an estimate forπ is given by
The iterative algorithms were independently published in 1975–1976 by physicist Eugene Salamin and scientist Richard Brent.[116] These avoid reliance on infinite series. An iterative algorithm repeats a specific calculation, each iteration using the outputs from prior steps as its inputs, and produces a result in each step that converges to the desired value. The approach was actually invented over 160 years earlier by Carl Friedrich Gauss, in what is now termed the arithmetic–geometric mean method (AGM method) or Gauss–Legendre algorithm.[116] As modified by Salamin and Brent, it is also referred to as the Brent–Salamin algorithm.
The iterative algorithms were widely used after 1980 because they are faster than infinite series algorithms: whereas infinite series typically increase the number of correct digits additively in successive terms, iterative algorithms generally multiply the number of correct digits at each step. For example, the Brent–Salamin algorithm doubles the number of digits in each iteration. In 1984, brothers John and Peter Borwein produced an iterative algorithm that quadruples the number of digits in each step; and in 1987, one that increases the number of digits five times in each step.[117] Iterative methods were used by Japanese mathematician Yasumasa Kanada to set several records for computing
Rapidly convergent series

Modern
This series converges much more rapidly than most arctan series, including Machin's formula.[120]Bill Gosper was the first to use it for advances in the calculation of
It produces about 14 digits of
In 2006, mathematician Simon Plouffe used the PSLQ integer relation algorithm[127] to generate several new formulae for
where q is e
Monte Carlo methods
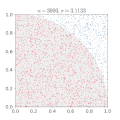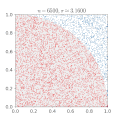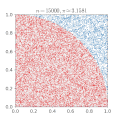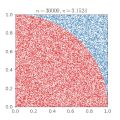
Monte Carlo methods, which evaluate the results of multiple random trials, can be used to create approximations of
Another Monte Carlo method for computing

Another way to calculate
so that, for each n, Wn is drawn from a shifted and scaled binomial distribution. As n varies, Wn defines a (discrete) stochastic process. Then
This Monte Carlo method is independent of any relation to circles, and is a consequence of the central limit theorem, discussed below.
These Monte Carlo methods for approximating
Spigot algorithms
Two algorithms were discovered in 1995 that opened up new avenues of research into
Mathematicians Stan Wagon and Stanley Rabinowitz produced a simple spigot algorithm in 1995.[135][136][137] Its speed is comparable to arctan algorithms, but not as fast as iterative algorithms.[136]
Another spigot algorithm, the BBP digit extraction algorithm, was discovered in 1995 by Simon Plouffe:[138][139]
This formula, unlike others before it, can produce any individual hexadecimal digit of
Between 1998 and 2000, the distributed computing project PiHex used Bellard's formula (a modification of the BBP algorithm) to compute the quadrillionth (1015th) bit of
In 2022, Plouffe found a base-10 algorithm for calculating digits of
Role and characterizations in mathematics
Because
Geometry and trigonometry

- The circumference of a circle with radius r is 2
π r.[145] - The area of a circle with radius r is
π r2. - The area of an ellipse with semi-major axis a and semi-minor axis b is
π ab.[146] - The volume of a sphere with radius r is 4/3
π r3. - The surface area of a sphere with radius r is 4
π r2.
Some of the formulae above are special cases of the volume of the n-dimensional ball and the surface area of its boundary, the (n−1)-dimensional sphere, given below.
Apart from circles, there are other curves of constant width. By Barbier's theorem, every curve of constant width has perimeter
Definite integrals that describe circumference, area, or volume of shapes generated by circles typically have values that involve
In that integral, the function represents the height over the -axis of a semicircle (the square root is a consequence of the Pythagorean theorem), and the integral computes the area below the semicircle. The existence of such integrals makes
Units of angle

The trigonometric functions rely on angles, and mathematicians generally use radians as units of measurement.
Common trigonometric functions have periods that are multiples of
Eigenvalues
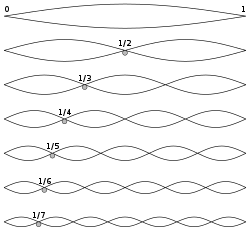
Many of the appearances of
In many applications, it plays a distinguished role as an eigenvalue. For example, an idealized vibrating string can be modelled as the graph of a function f on the unit interval [0, 1], with fixed ends f(0) = f(1) = 0. The modes of vibration of the string are solutions of the differential equation , or . Thus
The value
with equality precisely when f is a multiple of sin(
Inequalities

The number
and equality is clearly achieved for the circle, since in that case A =
Ultimately, as a consequence of the isoperimetric inequality,
for f a smooth function with compact support in R2, is the gradient of f, and and refer respectively to the L2 and L1-norm. The Sobolev inequality is equivalent to the isoperimetric inequality (in any dimension), with the same best constants.
Wirtinger's inequality also generalizes to higher-dimensional Poincaré inequalities that provide best constants for the Dirichlet energy of an n-dimensional membrane. Specifically,
for all convex subsets G of Rn of diameter 1, and square-integrable functions u on G of mean zero.[159] Just as Wirtinger's inequality is the variational form of the Dirichlet eigenvalue problem in one dimension, the Poincaré inequality is the variational form of the Neumann eigenvalue problem, in any dimension.
Fourier transform and Heisenberg uncertainty principle

The constant
Although there are several different conventions for the Fourier transform and its inverse, any such convention must involve
The Heisenberg uncertainty principle also contains the number
The physical consequence, about the uncertainty in simultaneous position and momentum observations of a quantum mechanical system, is discussed below. The appearance of
Gaussian integrals

The fields of probability and statistics frequently use the normal distribution as a simple model for complex phenomena; for example, scientists generally assume that the observational error in most experiments follows a normal distribution.[162] The Gaussian function, which is the probability density function of the normal distribution with mean
The factor of makes the area under the graph of f equal to one, as is required for a probability distribution. This follows from a change of variables in the Gaussian integral:[163]
which says that the area under the basic bell curve in the figure is equal to the square root of
The central limit theorem explains the central role of normal distributions, and thus of
Topology

The constant
where
reproducing the formula for the surface area of a sphere of radius 1.
The constant appears in many other integral formulae in topology, in particular, those involving characteristic classes via the Chern–Weil homomorphism.[167]
Cauchy's integral formula

One of the key tools in complex analysis is contour integration of a function over a positively oriented (rectifiable) Jordan curve
Although the curve
The general form of Cauchy's integral formula establishes the relationship between the values of a complex analytic function f(z) on the Jordan curve
provided f(z) is analytic in the region enclosed by
where the sum is of the residues at the poles of g(z).
Vector calculus and physics
The constant
The factor of is necessary to ensure that is the fundamental solution of the Poisson equation in :[173]
where is the Dirac delta function.
In higher dimensions, factors of
which has the 2-dimensional volume (i.e., the area) of the unit 2-sphere in the denominator.
Total curvature

In the differential geometry of curves, the total curvature of a smooth plane curve is the amount it turns anticlockwise, in radians, from start to finish, computed as the integral of signed curvature with respect to arc length:
For a closed curve, this quantity is equal to 2
The gamma function and Stirling's approximation

The factorial function is the product of all of the positive integers through n. The gamma function extends the concept of factorial (normally defined only for non-negative integers) to all complex numbers, except the negative real integers, with the identity . When the gamma function is evaluated at half-integers, the result contains
The gamma function is defined by its Weierstrass product development:[175]
where
The gamma function is used to calculate the volume Vn(r) of the n-dimensional ball of radius r in Euclidean n-dimensional space, and the surface area Sn−1(r) of its boundary, the (n−1)-dimensional sphere:[176]
Further, it follows from the functional equation that
The gamma function can be used to create a simple approximation to the factorial function n! for large n: which is known as Stirling's approximation.[177] Equivalently,
As a geometrical application of Stirling's approximation, let
Ehrhart's volume conjecture is that this is the (optimal) upper bound on the volume of a convex body containing only one lattice point.[178]
Number theory and Riemann zeta function


The Riemann zeta function
Finding a simple solution for this infinite series was a famous problem in mathematics called the Basel problem. Leonhard Euler solved it in 1735 when he showed it was equal to
This probability can be used in conjunction with a random number generator to approximate
The solution to the Basel problem implies that the geometrically derived quantity
The zeta function also satisfies Riemann's functional equation, which involves
Furthermore, the derivative of the zeta function satisfies
A consequence is that
Fourier series

The constant
There is a unique character on T, up to complex conjugation, that is a group isomorphism. Using the Haar measure on the circle group, the constant
Modular forms and theta functions

The constant
Modular forms are holomorphic functions in the upper half plane characterized by their transformation properties under the modular group (or its various subgroups), a lattice in the group . An example is the Jacobi theta function
which is a kind of modular form called a Jacobi form.[187] This is sometimes written in terms of the nome .
The constant
which implies that
Cauchy distribution and potential theory


is a probability density function. The total probability is equal to one, owing to the integral:
The Shannon entropy of the Cauchy distribution is equal to ln(4
The Cauchy distribution plays an important role in potential theory because it is the simplest Furstenberg measure, the classical Poisson kernel associated with a Brownian motion in a half-plane.[188] Conjugate harmonic functions and so also the Hilbert transform are associated with the asymptotics of the Poisson kernel. The Hilbert transform H is the integral transform given by the Cauchy principal value of the singular integral
The constant
In the Mandelbrot set

An occurrence of
Outside mathematics
Describing physical phenomena
Although not a physical constant,
One of the key formulae of quantum mechanics is Heisenberg's uncertainty principle, which shows that the uncertainty in the measurement of a particle's position (
The fact that
where me is the mass of the electron.
The field of fluid dynamics contains
In electromagnetics, the vacuum permeability constant
Memorizing digits
Piphilology is the practice of memorizing large numbers of digits of
One common technique is to memorize a story or poem in which the word lengths represent the digits of
A few authors have used the digits of
In popular culture

Perhaps because of the simplicity of its definition and its ubiquitous presence in formulae,
In the Palais de la Découverte (a science museum in Paris) there is a circular room known as the pi room. On its wall are inscribed 707 digits of
In Carl Sagan's 1985 novel Contact it is suggested that the creator of the universe buried a message deep within the digits of
In the United States, Pi Day falls on 14 March (written 3/14 in the US style), and is popular among students.[41]
Some have proposed replacing
In 1897, an amateur mathematician attempted to persuade the Indiana legislature to pass the Indiana Pi Bill, which described a method to square the circle and contained text that implied various incorrect values for
In contemporary internet culture, individuals and organizations frequently pay homage to the number
See also
References
Explanatory notes
- ^ The specific integral that Weierstrass used was[6]
- ^ The polynomial shown is the first few terms of the Taylor series expansion of the sine function.
- ^ The middle of these is due to the mid-17th century mathematician William Brouncker, see § Brouncker's formula.
Citations
- ^ a b Oughtred, William (1652). Theorematum in libris Archimedis de sphaera et cylindro declarario (in Latin). Excudebat L. Lichfield, Veneunt apud T. Robinson.
δ .π :: semidiameter. semiperipheria - ^ "pi". Dictionary.reference.com. 2 March 1993. Archived from the original on 28 July 2014. Retrieved 18 June 2012.
- ^ a b c Arndt & Haenel 2006, p. 8.
- ^ Apostol, Tom (1967). Calculus. Vol. 1 (2nd ed.). Wiley. p. 102.
From a logical point of view, this is unsatisfactory at the present stage because we have not yet discussed the concept of arc length
- ^ a b c Remmert 2012, p. 129.
- ^ Remmert 2012, p. 148. Weierstrass, Karl (1841). "Darstellung einer analytischen Function einer complexen Veränderlichen, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt" [Representation of an analytical function of a complex variable, whose absolute value lies between two given limits]. Mathematische Werke (in German). Vol. 1. Berlin: Mayer & Müller (published 1894). pp. 51–66.
- ^ Baltzer, Richard (1870). Die Elemente der Mathematik [The Elements of Mathematics] (in German). Hirzel. p. 195. Archived from the original on 14 September 2016.
- ^ Landau, Edmund (1934). Einführung in die Differentialrechnung und Integralrechnung (in German). Noordoff. p. 193.
- ^ a b Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. p. 183. ISBN 978-0-07-054235-8.
- ^ Rudin, Walter (1986). Real and complex analysis. McGraw-Hill. p. 2.
- ^ Ahlfors, Lars (1966). Complex analysis. McGraw-Hill. p. 46.
- ^ Bourbaki, Nicolas (1981). Topologie generale. Springer. §VIII.2.
- ^ a b Bourbaki, Nicolas (1979). Fonctions d'une variable réelle (in French). Springer. §II.3.
- ^ a b Arndt & Haenel 2006, p. 5.
- ^ Salikhov, V. (2008). "On the Irrationality Measure of pi". Russian Mathematical Surveys. 53 (3): 570–572. Bibcode:2008RuMaS..63..570S. doi:10.1070/RM2008v063n03ABEH004543. ISSN 0036-0279. S2CID 250798202.
- ^ Arndt & Haenel 2006, pp. 22–23.
- ^ Arndt & Haenel 2006, pp. 22, 28–30.
- ^ Arndt & Haenel 2006, p. 3.
- ^ Arndt & Haenel 2006, p. 6.
- ^ Posamentier & Lehmann 2004, p. 25.
- ^ Eymard & Lafon 2004, p. 129.
- ^ Beckmann, Petr (1989) [1974]. History of Pi. St. Martin's Press. p. 37. ISBN 978-0-88029-418-8. Schlager, Neil; Lauer, Josh (2001). Science and Its Times: Understanding the Social Significance of Scientific Discovery. Gale Group. ISBN 978-0-7876-3933-4. Archived from the original on 13 December 2019. Retrieved 19 December 2019., p. 185.
- ^ Murty, M. Ram; Rath, Purusottam (2014). Transcendental Numbers. Springer. doi:10.1007/978-1-4939-0832-5. ISBN 978-1-4939-0831-8. Waldschmidt, Michel (2021). "Schanuel's Conjecture: algebraic independence of transcendental numbers" (PDF).
- ^ Weisstein, Eric W. "Lindemann-Weierstrass Theorem". MathWorld.
- ^ a b Eymard & Lafon 2004, p. 78.
- ^ Arndt & Haenel 2006, p. 33.
- ^ a b Mollin, R. A. (1999). "Continued fraction gems". Nieuw Archief voor Wiskunde. 17 (3): 383–405. MR 1743850.
- ^ Lange, L. J. (May 1999). "An Elegant Continued Fraction for
π ". The American Mathematical Monthly. 106 (5): 456–458. doi:10.2307/2589152. JSTOR 2589152. - ^ Arndt & Haenel 2006, p. 240.
- ^ Arndt & Haenel 2006, p. 242.
- ^ Kennedy, E. S. (1978). "Abu-r-Raihan al-Biruni, 973–1048". Journal for the History of Astronomy. 9: 65. Bibcode:1978JHA.....9...65K. doi:10.1177/002182867800900106. S2CID 126383231. Ptolemy used a three-sexagesimal-digit approximation, and Jamshīd al-Kāshī expanded this to nine digits; see Aaboe, Asger (1964). Episodes from the Early History of Mathematics. New Mathematical Library. Vol. 13. New York: Random House. p. 125. ISBN 978-0-88385-613-0. Archived from the original on 29 November 2016.
{{cite book}}: ISBN / Date incompatibility (help) - ^ Abramson 2014, Section 8.5: Polar form of complex numbers.
- ^ a b Bronshteĭn & Semendiaev 1971, p. 592.
- ^ Maor, Eli (2009). E: The Story of a Number. Princeton University Press. p. 160. ISBN 978-0-691-14134-3.
- ^ Andrews, Askey & Roy 1999, p. 14.
- ^ a b Arndt & Haenel 2006, p. 167.
- ^ Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. pp. 67–77, 165–166. ISBN 978-0-88920-324-2. Retrieved 5 June 2013.
- ^ Plofker, Kim (2009). Mathematics in India. Princeton University Press. p. 27. ISBN 978-0-691-12067-6.
- ^ Arndt & Haenel 2006, p. 170.
- ^ Arndt & Haenel 2006, pp. 175, 205.
- ^ a b c Borwein, Jonathan M. (2014). "The life of
π : from Archimedes to ENIAC and beyond". In Sidoli, Nathan; Van Brummelen, Glen (eds.). From Alexandria, through Baghdad: Surveys and studies in the ancient Greek and medieval Islamic mathematical sciences in honor of J. L. Berggren. Heidelberg: Springer. pp. 531–561. doi:10.1007/978-3-642-36736-6_24. ISBN 978-3-642-36735-9. MR 3203895. - ^ Arndt & Haenel 2006, p. 171.
- ^ Arndt & Haenel 2006, p. 176.
- ^ Boyer & Merzbach 1991, p. 168.
- ^ Arndt & Haenel 2006, pp. 15–16, 175, 184–186, 205. Grienberger achieved 39 digits in 1630; Sharp 71 digits in 1699.
- ^ Arndt & Haenel 2006, pp. 176–177.
- ^ a b Boyer & Merzbach 1991, p. 202.
- ^ Arndt & Haenel 2006, p. 177.
- ^ Arndt & Haenel 2006, p. 178.
- ^ Arndt & Haenel 2006, p. 179.
- ^ a b Arndt & Haenel 2006, p. 180.
- ^ Azarian, Mohammad K. (2010). "al-Risāla al-muhītīyya: A Summary". Missouri Journal of Mathematical Sciences. 22 (2): 64–85. doi:10.35834/mjms/1312233136. O'Connor, John J.; Robertson, Edmund F. (1999). "Ghiyath al-Din Jamshid Mas'ud al-Kashi". MacTutor History of Mathematics archive. Archived from the original on 12 April 2011. Retrieved 11 August 2012.
- ^ a b c Arndt & Haenel 2006, p. 182.
- ^ Arndt & Haenel 2006, pp. 182–183.
- ^ Arndt & Haenel 2006, p. 183.
- ^ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (in Latin). Archived from the original (PDF) on 1 February 2014. His evaluation was 3.14159 26535 89793 23846 26433 83279 50288 4196 <
π < 3.14159 26535 89793 23846 26433 83279 50288 4199. - ^ Brezinski, C. (2009). "Some pioneers of extrapolation methods". In Bultheel, Adhemar; Cools, Ronald (eds.). The Birth of Numerical Analysis. World Scientific. pp. 1–22. doi:10.1142/9789812836267_0001. ISBN 978-981-283-625-0. Yoder, Joella G. (1996). "Following in the footsteps of geometry: The mathematical world of Christiaan Huygens". De Zeventiende Eeuw. 12: 83–93 – via Digital Library for Dutch Literature.
- ^ Arndt & Haenel 2006, pp. 185–191.
- ^ a b c d Roy, Ranjan (1990). "The Discovery of the Series Formula for
π by Leibniz, Gregory and Nilakantha" (PDF). Mathematics Magazine. 63 (5): 291–306. doi:10.1080/0025570X.1990.11977541. Archived from the original (PDF) on 14 March 2023. Retrieved 21 February 2023. - ^ Arndt & Haenel 2006, pp. 185–186.
- ^ Joseph, George Gheverghese (1991). The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press. p. 264. ISBN 978-0-691-13526-7.
- ^ Andrews, Askey & Roy 1999, p. 59.
- ^ Gupta, R. C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati. 14 (1–4): 68–71.
- ^ Arndt & Haenel 2006, p. 187. Vieta, Franciscus (1593). Variorum de rebus mathematicis responsorum. Vol. VIII. OEIS: A060294
- ^ Arndt & Haenel 2006, p. 187.
- ^ a b Arndt & Haenel 2006, p. 188. Newton quoted by Arndt.
- ^ Horvath, Miklos (1983). "On the Leibnizian quadrature of the circle" (PDF). Annales Universitatis Scientiarum Budapestiensis (Sectio Computatorica). 4: 75–83.
- ^ a b Eymard & Lafon 2004, pp. 53–54.
- ^ Cooker, M. J. (2011). "Fast formulas for slowly convergent alternating series" (PDF). Mathematical Gazette. 95 (533): 218–226. doi:10.1017/S0025557200002928. S2CID 123392772. Archived from the original (PDF) on 4 May 2019. Retrieved 23 February 2023.
- ^ Arndt & Haenel 2006, p. 189.
- ^ a b Jones, William (1706). Synopsis Palmariorum Matheseos. London: J. Wale. pp. 243, 263. p. 263:
There are various other ways of finding the Lengths, or Areas of particular Curve Lines or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to Circumference as 1 to
Reprinted in Smith, David Eugene (1929). "William Jones: The First Use of
3.14159, &c. =π . This Series (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. John Machin; and by means thereof, Van Ceulen's Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch.π for the Circle Ratio". A Source Book in Mathematics. McGraw–Hill. pp. 346–347. - ^ Tweddle, Ian (1991). "John Machin and Robert Simson on Inverse-tangent Series for
π ". Archive for History of Exact Sciences. 42 (1): 1–14. doi:10.1007/BF00384331. JSTOR 41133896. S2CID 121087222. - ^ Arndt & Haenel 2006, pp. 192–193.
- ^ a b Arndt & Haenel 2006, pp. 72–74.
- ^ Lehmer, D. H. (1938). "On Arccotangent Relations for
π " (PDF). American Mathematical Monthly. 45 (10): 657–664 Published by: Mathematical Association of America. doi:10.1080/00029890.1938.11990873. JSTOR 2302434. Archived from the original (PDF) on 7 March 2023. Retrieved 21 February 2023. - ^ Roy, Ranjan (2021) [1st ed. 2011]. Series and Products in the Development of Mathematics. Vol. 1 (2 ed.). Cambridge University Press. pp. 215–216, 219–220. Newton, Isaac (1971). "De computo serierum" [On the computation of series]. In Whiteside, Derek Thomas (ed.). The Mathematical Papers of Isaac Newton. Vol. 4, 1674–1684. Cambridge University Press. "De transmutatione serierum" [On the transformation of series] § 3.2.2 pp. 604–615.
- ^ Sandifer, Ed (2009). "Estimating
π " (PDF). How Euler Did It. Reprinted in How Euler Did Even More. Mathematical Association of America. 2014. pp. 109–118. Euler, Leonhard (1755). "§ 2.2.30". Institutiones Calculi Differentialis (in Latin). Academiae Imperialis Scientiarium Petropolitanae. p. 318. E 212. Euler, Leonhard (1798) [written 1779]. "Investigatio quarundam serierum, quae ad rationem peripheriae circuli ad diametrum vero proxime definiendam maxime sunt accommodatae". Nova Acta Academiae Scientiarum Petropolitinae. 11: 133–149, 167–168. E 705. Hwang, Chien-Lih (2004). "88.38 Some Observations on the Method of Arctangents for the Calculation ofπ ". Mathematical Gazette. 88 (512): 270–278. doi:10.1017/S0025557200175060. JSTOR 3620848. S2CID 123532808. Hwang, Chien-Lih (2005). "89.67 An elementary derivation of Euler's series for the arctangent function". Mathematical Gazette. 89 (516): 469–470. doi:10.1017/S0025557200178404. JSTOR 3621947. S2CID 123395287. - ^ Arndt & Haenel 2006, pp. 192–196, 205.
- ^ Arndt & Haenel 2006, pp. 194–196.
- ^ Hayes, Brian (September 2014). "Pencil, Paper, and Pi". American Scientist. Vol. 102, no. 5. p. 342. doi:10.1511/2014.110.342. Retrieved 22 January 2022.
- ^ a b Borwein, J. M.; Borwein, P. B. (1988). "Ramanujan and Pi". Scientific American. 256 (2): 112–117. Bibcode:1988SciAm.258b.112B. doi:10.1038/scientificamerican0288-112.
Arndt & Haenel 2006, pp. 15–17, 70–72, 104, 156, 192–197, 201–202. - ^ Arndt & Haenel 2006, pp. 69–72.
- ^ Borwein, J. M.; Borwein, P. B.; Dilcher, K. (1989). "Pi, Euler Numbers, and Asymptotic Expansions". American Mathematical Monthly. 96 (8): 681–687. doi:10.2307/2324715. hdl:1959.13/1043679. JSTOR 2324715.
- ^ Arndt & Haenel 2006, Formula 16.10, p. 223.
- ^ Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers (revised ed.). Penguin. p. 35. ISBN 978-0-14-026149-3.
- ^ a b Posamentier & Lehmann 2004, p. 284.
- ^ Lambert, Johann, "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", reprinted in Berggren, Borwein & Borwein 1997, pp. 129–140.
- ^ Lindemann, F. (1882). "Über die Ludolph'sche Zahl". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. 2: 679–682.
- ^ Arndt & Haenel 2006, p. 196.
- ^ Hardy and Wright 1938 and 2000: 177 footnote § 11.13–14 references Lindemann's proof as appearing at Math. Ann. 20 (1882), 213–225.
- ^ cf Hardy and Wright 1938 and 2000:177 footnote § 11.13–14. The proofs that e and
π are transcendental can be found on pp. 170–176. They cite two sources of the proofs at Landau 1927 or Perron 1910; see the "List of Books" at pp. 417–419 for full citations. - ^ Oughtred, William (1648). Clavis Mathematicæ [The key to mathematics] (in Latin). London: Thomas Harper. p. 69. (English translation: Oughtred, William (1694). Key of the Mathematics. J. Salusbury.)
- ^ a b c d Arndt & Haenel 2006, p. 166.
- ^ a b Cajori, Florian (2007). A History of Mathematical Notations: Vol. II. Cosimo, Inc. pp. 8–13. ISBN 978-1-60206-714-1.
the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented 3.14159... by
δ :π , as did Oughtred more than a century earlier - ^ a b Smith, David E. (1958). History of Mathematics. Courier Corporation. p. 312. ISBN 978-0-486-20430-7.
{{cite book}}: ISBN / Date incompatibility (help) - ^ Archibald, R. C. (1921). "Historical Notes on the Relation e−(
π /2) = ii". The American Mathematical Monthly. 28 (3): 116–121. doi:10.2307/2972388. JSTOR 2972388.It is noticeable that these letters are never used separately, that is,
π is not used for 'Semiperipheria' - ^ Barrow, Isaac (1860). "Lecture XXIV". In Whewell, William (ed.). The mathematical works of Isaac Barrow (in Latin). Harvard University. Cambridge University press. p. 381.
- ^ Gregorius, David (1695). "Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae" (PDF). Philosophical Transactions (in Latin). 19 (231): 637–652. Bibcode:1695RSPT...19..637G. doi:10.1098/rstl.1695.0114. JSTOR 102382.
- ^ Arndt & Haenel 2006, p. 165: A facsimile of Jones' text is in Berggren, Borwein & Borwein 1997, pp. 108–109.
- ^ Segner, Joannes Andreas (1756). Cursus Mathematicus (in Latin). Halae Magdeburgicae. p. 282. Archived from the original on 15 October 2017. Retrieved 15 October 2017.
- ^ Euler, Leonhard (1727). "Tentamen explicationis phaenomenorum aeris" (PDF). Commentarii Academiae Scientiarum Imperialis Petropolitana (in Latin). 2: 351. E007. Archived (PDF) from the original on 1 April 2016. Retrieved 15 October 2017.
Sumatur pro ratione radii ad peripheriem, I :
English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine: "π π is taken for the ratio of the radius to the periphery [note that in this work, Euler'sπ is double ourπ .]" Euler, Leonhard (1747). Henry, Charles (ed.). Lettres inédites d'Euler à d'Alembert. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche (in French). Vol. 19 (published 1886). p. 139. E858.Car, soit
English translation in Cajori, Florian (1913). "History of the Exponential and Logarithmic Concepts". The American Mathematical Monthly. 20 (3): 75–84. doi:10.2307/2973441. JSTOR 2973441.π la circonference d'un cercle, dout le rayon est = 1Letting
π be the circumference (!) of a circle of unit radius - ^ Euler, Leonhard (1736). "Ch. 3 Prop. 34 Cor. 1". Mechanica sive motus scientia analytice exposita. (cum tabulis) (in Latin). Vol. 1. Academiae scientiarum Petropoli. p. 113. E015.
Denotet 1 :
English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine : "Let 1 :π rationem diametri ad peripheriamπ denote the ratio of the diameter to the circumference" - ^ Euler, Leonhard (1922). Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio (in Latin). Lipsae: B. G. Teubneri. pp. 133–134. E101. Archived from the original on 16 October 2017. Retrieved 15 October 2017.
- ^ Segner, Johann Andreas von (1761). Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm (in Latin). Renger. p. 374.
Si autem
π notet peripheriam circuli, cuius diameter eſt 2 - ^ Arndt & Haenel 2006, pp. 17–19.
- ^ Schudel, Matt (25 March 2009). "John W. Wrench, Jr.: Mathematician Had a Taste for Pi". The Washington Post. p. B5. Connor, Steve (8 January 2010). "The Big Question: How close have we come to knowing the precise value of pi?". The Independent. London. Archived from the original on 2 April 2012. Retrieved 14 April 2012.
- ^ Arndt & Haenel 2006, pp. 17–18.
- ^ Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). "The quest for PI". The Mathematical Intelligencer. 19 (1): 50–56. CiteSeerX 10.1.1.138.7085. doi:10.1007/BF03024340. ISSN 0343-6993. S2CID 14318695.
- ^ Arndt & Haenel 2006, p. 205.
- ^ a b Arndt & Haenel 2006, p. 197.
- ^ Reitwiesner, George (1950). "An ENIAC Determination of pi and e to 2000 Decimal Places". Mathematical Tables and Other Aids to Computation. 4 (29): 11–15. doi:10.2307/2002695. JSTOR 2002695.
- ^ Nicholson, J. C.; Jeenel, J. (1955). "Some comments on a NORC Computation of
π ". Math. Tabl. Aids. Comp. 9 (52): 162–164. doi:10.2307/2002052. JSTOR 2002052. - ^ Arndt & Haenel 2006, pp. 15–17.
- ^ Arndt & Haenel 2006, p. 131.
- ^ Arndt & Haenel 2006, pp. 132, 140.
- ^ a b Arndt & Haenel 2006, p. 87.
- ^ Arndt & Haenel 2006, p. 111 (5 times); pp. 113–114 (4 times). For details of algorithms, see Borwein, Jonathan; Borwein, Peter (1987). Pi and the AGM: a Study in Analytic Number Theory and Computational Complexity. Wiley. ISBN 978-0-471-31515-5.
- ^ a b c Bailey, David H. (16 May 2003). "Some Background on Kanada's Recent Pi Calculation" (PDF). Archived (PDF) from the original on 15 April 2012. Retrieved 12 April 2012.
- ^ Arndt & Haenel 2006, pp. 103–104.
- ^ Arndt & Haenel 2006, p. 104.
- ^ Arndt & Haenel 2006, pp. 104, 206.
- ^ Arndt & Haenel 2006, pp. 110–111.
- ^ Eymard & Lafon 2004, p. 254.
- ^ a b Bailey, David H.; Borwein, Jonathan M. (2016). "15.2 Computational records". Pi: The Next Generation, A Sourcebook on the Recent History of Pi and Its Computation. Springer International Publishing. p. 469. doi:10.1007/978-3-319-32377-0. ISBN 978-3-319-32375-6.
- ^ Cassel, David (11 June 2022). "How Google's Emma Haruka Iwao Helped Set a New Record for Pi". The New Stack.
- ^ Haruka Iwao, Emma (14 March 2019). "Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes' constant on Google Cloud". Google Cloud Platform. Archived from the original on 19 October 2019. Retrieved 12 April 2019.
- ^ PSLQ means Partial Sum of Least Squares.
- ^ Plouffe, Simon (April 2006). "Identities inspired by Ramanujan's Notebooks (part 2)" (PDF). Archived (PDF) from the original on 14 January 2012. Retrieved 10 April 2009.
- ^ Arndt & Haenel 2006, p. 39.
- ^ Ramaley, J. F. (October 1969). "Buffon's Needle Problem". The American Mathematical Monthly. 76 (8): 916–918. doi:10.2307/2317945. JSTOR 2317945.
- ^ Arndt & Haenel 2006, pp. 39–40.
Posamentier & Lehmann 2004, p. 105. - ^ Grünbaum, B. (1960). "Projection Constants". Transactions of the American Mathematical Society. 95 (3): 451–465. doi:10.1090/s0002-9947-1960-0114110-9.
- ^ Arndt & Haenel 2006, p. 43.
Posamentier & Lehmann 2004, pp. 105–108. - ^ a b Arndt & Haenel 2006, pp. 77–84.
- ^ a b Gibbons, Jeremy (2006). "Unbounded spigot algorithms for the digits of pi" (PDF). The American Mathematical Monthly. 113 (4): 318–328. doi:10.2307/27641917. JSTOR 27641917. MR 2211758.
- ^ a b Arndt & Haenel 2006, p. 77.
- ^ Rabinowitz, Stanley; Wagon, Stan (March 1995). "A spigot algorithm for the digits of Pi". American Mathematical Monthly. 102 (3): 195–203. doi:10.2307/2975006. JSTOR 2975006.
- ^ a b Arndt & Haenel 2006, pp. 117, 126–128.
- ^ Bailey, David H.; Borwein, Peter B.; Plouffe, Simon (April 1997). "On the Rapid Computation of Various Polylogarithmic Constants" (PDF). Mathematics of Computation. 66 (218): 903–913. Bibcode:1997MaCom..66..903B. CiteSeerX 10.1.1.55.3762. doi:10.1090/S0025-5718-97-00856-9. S2CID 6109631. Archived (PDF) from the original on 22 July 2012.
- ^ Arndt & Haenel 2006, p. 20.
Bellards formula in: Bellard, Fabrice. "A new formula to compute the nth binary digit of pi". Archived from the original on 12 September 2007. Retrieved 27 October 2007. - ^ Palmer, Jason (16 September 2010). "Pi record smashed as team finds two-quadrillionth digit". BBC News. Archived from the original on 17 March 2011. Retrieved 26 March 2011.
- ^ Plouffe, Simon (2022). "A formula for the nth decimal digit or binary of
π and powers ofπ ". arXiv:2201.12601 [math.NT]. - ^ Weisstein, Eric W. "Circle". MathWorld.
- ^ Bronshteĭn & Semendiaev 1971, pp. 200, 209.
- ^ Weisstein, Eric W. "Circumference". MathWorld.
- ^ Weisstein, Eric W. "Ellipse". MathWorld.
- ^ Martini, Horst; Montejano, Luis; Oliveros, Déborah (2019). Bodies of Constant Width: An Introduction to Convex Geometry with Applications. Birkhäuser. doi:10.1007/978-3-030-03868-7. ISBN 978-3-030-03866-3. MR 3930585. S2CID 127264210.
See Barbier's theorem, Corollary 5.1.1, p. 98; Reuleaux triangles, pp. 3, 10; smooth curves such as an analytic curve due to Rabinowitz, § 5.3.3, pp. 111–112.
- ^ Herman, Edwin; Strang, Gilbert (2016). "Section 5.5, Exercise 316". Calculus. Vol. 1. OpenStax. p. 594.
- ^ Kontsevich, Maxim; Zagier, Don (2001). "Periods". In Engquist, Björn; Schmid, Wilfried (eds.). Mathematics Unlimited — 2001 and Beyond. Berlin, Heidelberg: Springer. pp. 771–808. doi:10.1007/978-3-642-56478-9_39. ISBN 978-3-642-56478-9.
- ^ Abramson 2014, Section 5.1: Angles.
- ^ Bronshteĭn & Semendiaev 1971, pp. 210–211.
- ^ Hilbert, David; Courant, Richard (1966). Methods of mathematical physics. Vol. 1. Wiley. pp. 286–290.
- ^ Dym & McKean 1972, p. 47.
- ^ Thompson, William (1894). "Isoperimetrical problems". Nature Series: Popular Lectures and Addresses. II: 571–592.
- ^ Chavel, Isaac (2001). Isoperimetric inequalities. Cambridge University Press.
- ^ Talenti, Giorgio (1976). "Best constant in Sobolev inequality". Annali di Matematica Pura ed Applicata. 110 (1): 353–372. CiteSeerX 10.1.1.615.4193. doi:10.1007/BF02418013. ISSN 1618-1891. S2CID 16923822.
- ^ L. Esposito; C. Nitsch; C. Trombetti (2011). "Best constants in Poincaré inequalities for convex domains". arXiv:1110.2960 [math.AP].
- ^ Del Pino, M.; Dolbeault, J. (2002). "Best constants for Gagliardo–Nirenberg inequalities and applications to nonlinear diffusions". Journal de Mathématiques Pures et Appliquées. 81 (9): 847–875. CiteSeerX 10.1.1.57.7077. doi:10.1016/s0021-7824(02)01266-7. S2CID 8409465.
- ^ Payne, L. E.; Weinberger, H. F. (1960). "An optimal Poincaré inequality for convex domains". Archive for Rational Mechanics and Analysis. 5 (1): 286–292. Bibcode:1960ArRMA...5..286P. doi:10.1007/BF00252910. ISSN 0003-9527. S2CID 121881343.
- ^ Folland, Gerald (1989). Harmonic analysis in phase space. Princeton University Press. p. 5.
- ^ a b Howe, Roger (1980). "On the role of the Heisenberg group in harmonic analysis". Bulletin of the American Mathematical Society. 3 (2): 821–844. doi:10.1090/S0273-0979-1980-14825-9. MR 0578375.
- ^ Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, Wiley, 1968, pp. 174–190.
- ^ a b Bronshteĭn & Semendiaev 1971, pp. 106–107, 744, 748.
- ^ Dym & McKean 1972, Section 2.7.
- ^ Stein, Elias; Weiss, Guido (1971). Fourier analysis on Euclidean spaces. Princeton University Press. p. 6.; Theorem 1.13.
- ^ Spivak, Michael (1999). A Comprehensive Introduction to Differential Geometry. Vol. 3. Publish or Perish Press.; Chapter 6.
- ^ Kobayashi, Shoshichi; Nomizu, Katsumi (1996). Foundations of Differential Geometry. Vol. 2 (New ed.). Wiley Interscience. p. 293.; Chapter XII Characteristic classes
- ^ Ahlfors, Lars (1966). Complex analysis. McGraw-Hill. p. 115.
- ^ Joglekar, S. D. (2005). Mathematical Physics. Universities Press. p. 166. ISBN 978-81-7371-422-1.
- ^ Schey, H. M. (1996). Div, Grad, Curl, and All That: An Informal Text on Vector Calculus. W. W. Norton. ISBN 0-393-96997-5.
- ^ Yeo, Adrian (2006). The pleasures of pi, e and other interesting numbers. World Scientific Pub. p. 21. ISBN 978-981-270-078-0.
- ^ Ehlers, Jürgen (2000). Einstein's Field Equations and Their Physical Implications. Springer. p. 7. ISBN 978-3-540-67073-5.
- ^ a b Gilbarg, D.; Trudinger, Neil (1983). Elliptic Partial Differential Equations of Second Order. New York: Springer. ISBN 3-540-41160-7.
- ^ Bronshteĭn & Semendiaev 1971, pp. 191–192.
- ^ Artin, Emil (1964). The Gamma Function. Athena series; selected topics in mathematics (1st ed.). Holt, Rinehart and Winston.
- ^ Evans, Lawrence (1997). Partial Differential Equations. AMS. p. 615.
- ^ Bronshteĭn & Semendiaev 1971, p. 190.
- ^ Benjamin Nill; Andreas Paffenholz (2014). "On the equality case in Erhart's volume conjecture". Advances in Geometry. 14 (4): 579–586. arXiv:1205.1270. doi:10.1515/advgeom-2014-0001. ISSN 1615-7168. S2CID 119125713.
- ^ Arndt & Haenel 2006, pp. 41–43. This theorem was proved by Ernesto Cesàro in 1881. For a more rigorous proof than the intuitive and informal one given here, see Hardy, G. H. (2008). An Introduction to the Theory of Numbers. Oxford University Press. Theorem 332. ISBN 978-0-19-921986-5.
- ^ Ogilvy, C. S.; Anderson, J. T. (1988). Excursions in Number Theory. Dover. pp. 29–35. ISBN 0-486-25778-9.
- ^ Arndt & Haenel 2006, p. 43.
- ^ Platonov, Vladimir; Rapinchuk, Andrei (1994). Algebraic Groups and Number Theory. Academic Press. pp. 262–265.
- ^ Sondow, J. (1994). "Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series". Proceedings of the American Mathematical Society. 120 (2): 421–424. CiteSeerX 10.1.1.352.5774. doi:10.1090/s0002-9939-1994-1172954-7. S2CID 122276856.
- ^ Friedmann, T.; Hagen, C. R. (2015). "Quantum mechanical derivation of the Wallis formula for pi". Journal of Mathematical Physics. 56 (11): 112101. arXiv:1510.07813. Bibcode:2015JMP....56k2101F. doi:10.1063/1.4930800. S2CID 119315853.
- ^ Tate, John T. (1950). "Fourier analysis in number fields, and Hecke's zeta-functions". In Cassels, J. W. S.; Fröhlich, A. (eds.). Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965). Thompson, Washington, DC. pp. 305–347. ISBN 978-0-9502734-2-6. MR 0217026.
{{cite conference}}: ISBN / Date incompatibility (help) - ^ Dym & McKean 1972, Chapter 4.
- ^ a b Mumford, David (1983). Tata Lectures on Theta I. Boston: Birkhauser. pp. 1–117. ISBN 978-3-7643-3109-2.
- ^ Port, Sidney; Stone, Charles (1978). Brownian motion and classical potential theory. Academic Press. p. 29.
- ^ Titchmarsh, E. (1948). Introduction to the Theory of Fourier Integrals (2nd ed.). Oxford University: Clarendon Press (published 1986). ISBN 978-0-8284-0324-5.
{{cite book}}: ISBN / Date incompatibility (help) - ^ Stein, Elias (1970). Singular Integrals and Differentiability Properties of Functions. Princeton University Press.; Chapter II.
- ^ Klebanoff, Aaron (2001). "Pi in the Mandelbrot set" (PDF). Fractals. 9 (4): 393–402. doi:10.1142/S0218348X01000828. Archived from the original (PDF) on 27 October 2011. Retrieved 14 April 2012. Peitgen, Heinz-Otto (2004). Chaos and fractals: new frontiers of science. Springer. pp. 801–803. ISBN 978-0-387-20229-7.
- ^ Halliday, David; Resnick, Robert; Walker, Jearl (1997). Fundamentals of Physics (5th ed.). John Wiley & Sons. p. 381. ISBN 0-471-14854-7.
- ^ Urone, Paul Peter; Hinrichs, Roger (2022). "29.7 Probability: The Heisenberg Uncertainty Principle". College Physics 2e. OpenStax.
- ^ Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory (2005 ed.). Mineola, NY: Dover Publications. ISBN 978-0-486-44568-7. LCCN 2005053026. OCLC 61200849.
- ^ Low, Peter (1971). Classical Theory of Structures Based on the Differential Equation. Cambridge University Press. pp. 116–118. ISBN 978-0-521-08089-7.
- ^ Batchelor, G. K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. p. 233. ISBN 0-521-66396-2.
- ^ a b c Arndt & Haenel 2006, pp. 44–45.
- ^ "Most Pi Places Memorized" Archived 14 February 2016 at the Wayback Machine, Guinness World Records.
- ^ Otake, Tomoko (17 December 2006). "How can anyone remember 100,000 numbers?". The Japan Times. Archived from the original on 18 August 2013. Retrieved 27 October 2007.
- ^ Danesi, Marcel (January 2021). "Chapter 4: Pi in Popular Culture". Pi (
π ) in Nature, Art, and Culture. Brill. p. 97. doi:10.1163/9789004433397. ISBN 9789004433373. S2CID 224869535. - ^ Raz, A.; Packard, M. G. (2009). "A slice of pi: An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist". Neurocase. 15 (5): 361–372. doi:10.1080/13554790902776896. PMC 4323087. PMID 19585350.
- ^ Keith, Mike. "Cadaeic Cadenza Notes & Commentary". Archived from the original on 18 January 2009. Retrieved 29 July 2009.
- ^ Keith, Michael; Diana Keith (17 February 2010). Not A Wake: A dream embodying (pi)'s digits fully for 10,000 decimals. Vinculum Press. ISBN 978-0-9630097-1-5.
- ^ For instance, Pickover calls
π "the most famous mathematical constant of all time", and Peterson writes, "Of all known mathematical constants, however, pi continues to attract the most attention", citing the Givenchyπ perfume, Pi (film), and Pi Day as examples. See: Pickover, Clifford A. (1995). Keys to Infinity. Wiley & Sons. p. 59. ISBN 978-0-471-11857-2. Peterson, Ivars (2002). Mathematical Treks: From Surreal Numbers to Magic Circles. MAA spectrum. Mathematical Association of America. p. 17. ISBN 978-0-88385-537-9. Archived from the original on 29 November 2016. - ^ Posamentier & Lehmann 2004, p. 118.
Arndt & Haenel 2006, p. 50. - ^ Arndt & Haenel 2006, p. 14. Polster, Burkard; Ross, Marty (2012). Math Goes to the Movies. Johns Hopkins University Press. pp. 56–57. ISBN 978-1-4214-0484-4.
- ^ Gill, Andy (4 November 2005). "Review of Aerial". The Independent. Archived from the original on 15 October 2006.
the almost autistic satisfaction of the obsessive-compulsive mathematician fascinated by 'Pi' (which affords the opportunity to hear Bush slowly sing vast chunks of the number in question, several dozen digits long)
- ^ Rubillo, James M. (January 1989). "Disintegrate 'em". The Mathematics Teacher. 82 (1): 10. JSTOR 27966082. Petroski, Henry (2011). Title An Engineer's Alphabet: Gleanings from the Softer Side of a Profession. Cambridge University Press. p. 47. ISBN 978-1-139-50530-7.
- ^ "Happy Pi Day! Watch these stunning videos of kids reciting 3.14". USAToday.com. 14 March 2015. Archived from the original on 15 March 2015. Retrieved 14 March 2015. Rosenthal, Jeffrey S. (February 2015). "Pi Instant". Math Horizons. 22 (3): 22. doi:10.4169/mathhorizons.22.3.22. S2CID 218542599.
- ^ Griffin, Andrew. "Pi Day: Why some mathematicians refuse to celebrate 14 March and won't observe the dessert-filled day". The Independent. Archived from the original on 24 April 2019. Retrieved 2 February 2019.
- ^ Freiberger, Marianne; Thomas, Rachel (2015). "Tau – the new
π ". Numericon: A Journey through the Hidden Lives of Numbers. Quercus. p. 159. ISBN 978-1-62365-411-5. Abbott, Stephen (April 2012). "My Conversion to Tauism" (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. S2CID 126179022. Archived (PDF) from the original on 28 September 2013. - ^ Palais, Robert (2001). "
π Is Wrong!" (PDF). The Mathematical Intelligencer. 23 (3): 7–8. doi:10.1007/BF03026846. S2CID 120965049. Archived (PDF) from the original on 22 June 2012. - ^ "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 30 June 2011. Archived from the original on 13 July 2013.
- ^ Conover, Emily (14 March 2018). "Forget Pi Day. We should be celebrating Tau Day". Science News. Retrieved 2 May 2023.
- ^ Arndt & Haenel 2006, pp. 211–212.
Posamentier & Lehmann 2004, pp. 36–37.
Hallerberg, Arthur (May 1977). "Indiana's squared circle". Mathematics Magazine. 50 (3): 136–140. doi:10.2307/2689499. JSTOR 2689499. - ^ Knuth, Donald (3 October 1990). "The Future of TeX and Metafont" (PDF). TeX Mag. 5 (1): 145. Archived (PDF) from the original on 13 April 2016. Retrieved 17 February 2017.
Sources
- Abramson, Jay (2014). Precalculus. OpenStax.
- Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special Functions. Cambridge: University Press. ISBN 978-0-521-78988-2.
- Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Retrieved 5 June 2013. English translation by Catriona and David Lischka.
- Berggren, Lennart; Borwein, Jonathan; Borwein, Peter (1997). Pi: a Source Book. Springer-Verlag. ISBN 978-0-387-20571-7.
- Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics (2 ed.). Wiley. ISBN 978-0-471-54397-8.
- Bronshteĭn, Ilia; Semendiaev, K. A. (1971). A Guide Book to Mathematics. Verlag Harri Deutsch. ISBN 978-3-87144-095-3.
- Dym, H.; McKean, H. P. (1972). Fourier series and integrals. Academic Press.
- Eymard, Pierre; Lafon, Jean Pierre (2004). The Number
π . Translated by Wilson, Stephen. American Mathematical Society. ISBN 978-0-8218-3246-2. English translation of Autour du nombreπ (in French). Hermann. 1999. - Posamentier, Alfred S.; Lehmann, Ingmar (2004).
π : A Biography of the World's Most Mysterious Number. Prometheus Books. ISBN 978-1-59102-200-8. - Remmert, Reinhold (2012). "Ch. 5 What is
π ?". In Heinz-Dieter Ebbinghaus; Hans Hermes; Friedrich Hirzebruch; Max Koecher; Klaus Mainzer; Jürgen Neukirch; Alexander Prestel; Reinhold Remmert (eds.). Numbers. Springer. ISBN 978-1-4612-1005-4.
Further reading
- Blatner, David (1999). The Joy of
π . Walker & Company. ISBN 978-0-8027-7562-7. - Delahaye, Jean-Paul (1997). Le fascinant nombre
π . Paris: Bibliothèque Pour la Science. ISBN 2-902918-25-9.
External links
- Weisstein, Eric W. "Pi". MathWorld.
- Demonstration by Lambert (1761) of irrationality of
π , online Archived 31 December 2014 at the Wayback Machine and analysed BibNum Archived 2 April 2015 at the Wayback Machine (PDF). π Search Engine 2 billion searchable digits ofπ , e and √2- approximation von
π by lattice points and approximation ofπ with rectangles and trapezoids (interactive illustrations)









![{\displaystyle {\sqrt[{3}]{31}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fb1cd8b2742403364f3adca4fc8b8ca4a21e7f5)














































![{\displaystyle \pi =\lim _{n\to \infty }{\frac {2n}{E[|W_{n}|]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a691be63815c6b7d9fe15070ae98039d9c1d0384)








![{\displaystyle f:[0,1]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0468f15485d405d64092878cda0fc0cbdab2f62)

![{\displaystyle H_{0}^{1}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7113d194de39d54621e9da47782ad5263b9f1790)






































![{\displaystyle {\begin{aligned}\prod _{p}^{\infty }\left(1-{\frac {1}{p^{2}}}\right)&=\left(\prod _{p}^{\infty }{\frac {1}{1-p^{-2}}}\right)^{-1}\\[4pt]&={\frac {1}{1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots }}\\[4pt]&={\frac {1}{\zeta (2)}}={\frac {6}{\pi ^{2}}}\approx 61\%.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33ad11b6609d91487577949c7a42872afdc33a36)


















