Funtzio trigonometriko

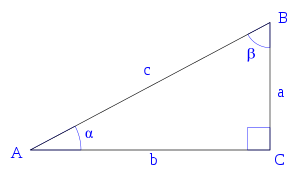
Triangelu angeluzuzen bateko angeluen eta aldeen notazioa

Triangelu angeluzuzen batean, funtzio trigonometrikoa aldeen neurrien arteko erlazioak adierazten dituzten funtzioetako edozein da. Funtzio nagusiak sei dira: sinua, kosinua, tangentea, kosekantea, sekantea eta kotangentea. (Ikusi irudia) ABC triangelu angeluzuzen bat izanik, C angelu zuzena dela eta a, b eta c, hurrenez hurren, A, B eta C angeluen aurrez aurreko aldeak direla, funtzio trigonometrikoak hauek dira:

$\sin \alpha ={\frac {\textrm {aurkakoa}}{\textrm {hipotenusa}}}=\color {Blue}{\frac {a}{c}}$

$\cos \alpha ={\frac {\textrm {albokoa}}{\textrm {hipotenusa}}}=\color {Blue}{\frac {b}{c}}$

$\tan \alpha ={\frac {\textrm {aurkakoa}}{\textrm {albokoa}}}=\color {Blue}{\frac {a}{b}}$

$\cot \alpha ={\frac {\textrm {albokoa}}{\textrm {aurkakoa}}}=\color {Blue}{\frac {b}{a}}$

$\sec \alpha ={\frac {\textrm {hipotenusa}}{\textrm {albokoa}}}=\color {Blue}{\frac {h}{b}}$

$\csc \alpha ={\frac {\textrm {hipotenusa}}{\textrm {aurkakoa}}}=\color {Blue}{\frac {h}{a}}$

Kontzeptu orokorrak

Funtzio trigonometrikoak triangelu zuzen baten bi aldeen arteko zatidura gisa defini daitezke, haien angeluekin lotuta. Funtzio trigonometrikoak, zirkulu unitate batean (erradio unitarioa) marraztutako triangelu zuzen batean, erlazio trigonometrikoaren kontzeptuaren luzapenak diren funtzioak dira. Definizio modernoagoek serie infinitu edo ekuazio diferentzial batzuen soluzio gisa deskribatzen dituzte, balio positiboetara eta negatiboetara hedatzea ahalbidetuz, eta baita zenbaki konplexuetara ere.

Oinarrizko sei funtzio trigonometriko daude. Azken laurak lehenengo bi funtzioei dagokienez definitzen dira, nahiz eta geometrikoki edo haien erlazioen bidez defini daitezkeen. Funtzio batzuk ohikoak ziren iraganean, eta lehenengo tauletan agertzen dira, baina gaur egun ez dira erabiltzen; adibidez birsena (1 − cos θしーた) eta exsekantea (sec θしーた − 1).

Funtzioa	Laburdura	Baliokidetasunak (radianetan)
Sinu	Sin	$\sin \;\theta \equiv {\frac {1}{\csc \theta }}\equiv \cos \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\cos \theta }{\cot \theta }}\,$
Kosinua	cos	$\cos \theta \equiv {\frac {1}{\sec \theta }}\equiv \sin \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\sin \theta }{\tan \theta }}\,$
Tangentea	tan	$\tan \theta \equiv {\frac {1}{\cot \theta }}\equiv \cot \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\sin \theta }{\cos \theta }}\,$
Kotangentea	cot	$\cot \theta \equiv {\frac {1}{\tan \theta }}\equiv \tan \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\cos \theta }{\sin \theta }}\,$
Sekantea	sec	$\sec \theta \equiv {\frac {1}{\cos \theta }}\equiv \csc \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\tan \theta }{\sin \theta }}\,$
Kosekantea	csc	$\csc \theta \equiv {\frac {1}{\sin \theta }}\equiv \sec \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\cot \theta }{\cos \theta }}\,$

Angelu nabarien funtzio trigonometrikoak

	0°	30°	45°	60°	90°
sin	$0$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$	$1$
cos	$1$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {1}{2}}$	$0$
tan	$0$	${\frac {\sqrt {3}}{3}}$	$1$	${\sqrt {3}}$	$\infty$
cot	$\infty$	${\sqrt {3}}$	$1$	${\frac {\sqrt {3}}{3}}$	$0$
sec	$1$	${\frac {2{\sqrt {3}}}{3}}$	${\sqrt {2}}$	$2$	$\infty$
csc	$\infty$	$2$	${\sqrt {2}}$	${\frac {2{\sqrt {3}}}{3}}$	$1$

Adierazpen grafikoak

Identitateak

Identitate pitagorikoak

$\sin ^{2}(x)+\cos ^{2}(x)=1,\qquad \sec ^{2}(x)-\tan ^{2}(x)=1,\qquad \csc ^{2}(x)-\cot ^{2}(x)=1$

Angelu batuketa eta kenketa

$\sin(x\pm y)=\sin(x)\cos(y)\pm \cos(x)\sin(y)$	,	$\csc(x\pm y)={\frac {1}{\sin(x\pm y)}}$
$\cos(x\pm y)=\cos(x)\cos(y)\mp \sin(x)\sin(y)$	,	$\sec(x\pm y)={\frac {1}{\cos(x\pm y)}}$
$\tan(x\pm y)={\frac {\tan(x)\pm \tan(y)}{1\mp \tan(x)\tan(y)}}$	,	$\cot(x\pm y)={\frac {\cot(x)\cot(y)\mp 1}{\cot(y)\pm \cot(x)}}$

Angelu bikoitza eta erdia

$\sin(2x)={\frac {2\tan(x)}{1+\tan ^{2}(x)}}=2\sin(x)\cos(x)$	,	$\csc(2x)={\frac {1}{\sin(2x)}}$
$\cos(2x)={\frac {1-\tan ^{2}(x)}{1+\tan ^{2}(x)}}=\cos ^{2}(x)-\sin ^{2}(x)=2\cos ^{2}(x)-1$	,	$\sec(2x)={\frac {1}{\cos(2x)}}$
$\tan(2x)={\frac {2\tan(x)}{1-\tan ^{2}(x)}}$	,	$\cot(2x)={\frac {\cot ^{2}(x)-1}{2\cot(x)}}$

$\sin(x/2)=\pm {\sqrt {\frac {1-\cos(x)}{2}}}$	,	$\csc(x/2)={\frac {1}{\sin(x/2)}}$
$\cos(x/2)=\pm {\sqrt {\frac {1+\cos(x)}{2}}}$	,	$\sec(x/2)={\frac {1}{\cos(x/2)}}$
$\tan(x/2)=\csc(x)-\cot(x)=\pm {\sqrt {\frac {1-\cos(x)}{1+\cos(x)}}}={\frac {\sin(x)}{1+\cos(x)}}$	,	$\cot(x/2)=\csc(x)+\cot(x)$

Biderketatik batuketara

$\sin(x)\sin(y)={\frac {\cos(x-y)-\cos(x+y)}{2}}$	,	$\sin(x)\cos(y)={\frac {\sin(x+y)+\sin(x-y)}{2}}$
$\cos(x)\cos(y)={\frac {\cos(x+y)+\cos(x-y)}{2}}$	,	$\cos(x)\sin(y)={\frac {\sin(x+y)-\sin(x-y)}{2}}$

$\sin ^{2}(x)-\sin ^{2}(y)=\sin(x+y)\sin(x-y)$

$\cos ^{2}(x)-\sin ^{2}(y)=\cos(x+y)\cos(x-y)$

$\sin ^{2}(x)\cos ^{2}(x)={\frac {1-\cos(4x)}{8}}$

Batuketatik biderketara

$\sin(x)+\sin(y)=2\sin \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)$	,	$\sin(x)-\sin(y)=2\sin \left({\frac {x-y}{2}}\right)\cos \left({\frac {x+y}{2}}\right)$
$\cos(x)+\cos(y)=2\cos \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)$	,	$\cos(x)-\cos(y)=-2\sin \left({\frac {x+y}{2}}\right)\sin \left({\frac {x-y}{2}}\right)$
$\tan(x)+\tan(y)={\frac {\sin(x+y)}{\cos(x)\cos(y)}}$	,	$\tan(x)-\tan(y)={\frac {\sin(x-y)}{\cos(x)\cos(y)}}$

Berreketak

$\sin ^{2}(x)={\frac {1-\cos(2x)}{2}}$

$\quad$

$\cos ^{2}(x)={\frac {1+\cos(2x)}{2}}$

$\quad$

$\tan ^{2}(x)={\frac {1-\cos(2x)}{1+\cos(2x)}}$

$\sin ^{2}(x)-\sin ^{2}(y)=\sin(x+y)\sin(x-y)$

$\cos ^{2}(x)-\sin ^{2}(y)=\cos(x+y)\cos(x-y)$

$\sin ^{2}(x)\cos ^{2}(x)={\frac {1-\cos(4x)}{8}}$

Deribatuak

${\frac {d}{dx}}\sin(x)=\cos(x)$

${\frac {d}{dx}}\cos(x)=-\sin(x)$

${\frac {d}{dx}}\tan(x)=\sec ^{2}(x)=1+\tan ^{2}(x)$

${\frac {d}{dx}}\csc(x)=-\csc(x)\cot(x)$

${\frac {d}{dx}}\sec(x)=\sec(x)\tan(x)$

${\frac {d}{dx}}\cot(x)=-\csc ^{2}(x)=-(1+\cot ^{2}(x))$

Integralak

Funtzio trigonometrikoen integralen zerrenda

$\int \sin(x)dx=-\cos(x)+C$

$\int \cos(x)dx=\sin(x)+C$

$\int \tan(x)dx=-\ln |\cos(x)|+C$

$\int \csc(x)dx=-\ln |\csc(x)+\cot(x)|+C$

$\int \sec(x)dx=\ln |\sec(x)+\tan(x)|+C$

$\int \cot(x)dx=\ln |\sin(x)|+C$

Teoremak

Sinuaren teorema. $ABC$ triangelu batean $\alpha ,\beta ,\gamma$ hurrenez hurren $a,b,c$ aldeen aurkako angeluak baldin badira, orduan betetzen da:

${\frac {a}{\sin(\alpha )}}={\frac {b}{\sin(\beta )}}={\frac {c}{\sin(\gamma )}}$

Kosinuaren teorema. $ABC$ triangelu batean $\alpha ,\beta ,\gamma$ hurrenez hurren $a,b,c$ aldeen aurkako angeluak baldin badira, orduan betetzen da:

$a^{2}=b^{2}+c^{2}-2bc\cos(\alpha ),\quad b^{2}=a^{2}+c^{2}-2ac\cos(\beta ),\quad c^{2}=a^{2}+b^{2}-2ab\cos(\gamma )$

Tangentearen teorema. $ABC$ triangelu batean $\alpha ,\beta ,\gamma$ hurrenez hurren $a,b,c$ aldeen aurkako angeluak baldin badira, orduan betetzen da:

${\frac {a-b}{a+b}}={\frac {\tan \left({\frac {\alpha -\beta }{2}}\right)}{\tan \left({\frac {\alpha +\beta }{2}}\right)}},\quad {\frac {b-c}{b+c}}={\frac {\tan \left({\frac {\beta -\gamma }{2}}\right)}{\tan \left({\frac {\beta +\gamma }{2}}\right)}},\quad {\frac {a-c}{a+c}}={\frac {\tan \left({\frac {\alpha -\gamma }{2}}\right)}{\tan \left({\frac {\alpha +\gamma }{2}}\right)}}$

Kanpo estekak

• Datuak: Q93344
• Multimedia: Trigonometric functions / Q93344