量子色力学

標準ひょうじゅん模型もけい
標準ひょうじゅん模型もけいの素粒子そりゅうし
背景はいけい 素粒子そりゅうし物理ぶつり学がく 場ばの量子りょうし論ろん ゲージ理論りろん 自発じはつ的てき対称たいしょう性せいの破やぶれ ヒッグス機構きこう 構成こうせい要素ようそ 電でん弱じゃく相互そうご作用さよう 量子りょうし色しょく力学りきがく CKM行列ぎょうれつ 制約せいやく 強つよいCP問題もんだい 階層かいそう性せい問題もんだい ニュートリノ振動しんどう 理論りろん家か スダルシャン · マーシャク · ファインマン · ゲルマン · 坂田さかた · グラショー · ツワイク · 南部なんぶ · ハン · カビボ · ワインバーグ · サラーム · 小林こばやし · 益えき川がわ · トホーフト · フェルトマン · グロス · ポリツァー · ウィルチェック

量子りょうし色しょく力学りきがく（りょうしいろりきがく、quantum chromodynamics）とは「強つよい相互そうご作用さよう」を説明せつめいする、 SU(3) ゲージ対称たいしょう性せいに基もとづくゲージ場じょうの量子りょうし論ろんである。

色いろ

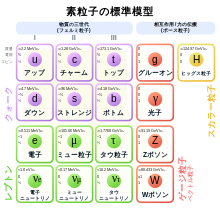
クォークとグルーオンは、カラーチャージ（color charge、色いろ荷に）と呼よばれる量子りょうし数すうを持もつ。カラーチャージは、光ひかりの三原色さんげんしょくからの類推るいすいにより「赤あか」、「緑みどり」、「青あお」と呼よばれることがある。カラーチャージを持もたない状態じょうたいは「白色はくしょく」であるとも呼よばれる。これは SU(3) リー代数だいすうの表現ひょうげんを分わかりやすい言葉ことばで表あらわしたものである。クォークは SU(3) の基本きほん表現ひょうげん 3（三重みえ項こう）を作つくり、反はんクォークは基本きほん表現ひょうげん 3（反はん三重みえ項こう）をなす。3 は「色いろ」の類推るいすいで言いえば「補色ほしょく」に対応たいおうしている。グルーオンは随伴ずいはん表現ひょうげん 8（八はち重じゅう項こう）で、「色いろ」と「補色ほしょく」を共ともに持もつ8つの状態じょうたいがある（3 × 3 から、「白色はくしょく」（一いち重じゅう項こう）となる組くみ合あわせが取とり除のぞかれる）。

カラーチャージはグルーオンと呼よぶゲージ粒子りゅうしを交換こうかんすることでやり取とりされ、これが強つよい相互そうご作用さようの源みなもとになっている。この相互そうご作用さようはカラーチャージ間あいだの距離きょりが小ちいさくなる（交換こうかんされる運動うんどう量りょうが高たかくなる）と弱よわくなるという、漸近ぜんきん的てき自由じゆう性せいを示しめす。逆ぎゃくに距離きょりが大おおきくなると相互そうご作用さようが強つよまり一定いっていの力ちからに近ちかづく。この結果けっかクォークを単体たんたいで取とり出だすことはできない。これは、現実げんじつに観測かんそくされるハドロンの状態じょうたいは「白色はくしょく」に限かぎられるという、クォークの閉とじ込こめ現象げんしょうを説明せつめいする。

「白色はくしょく」状態じょうたいを作つくるには、三原色さんげんしょくを持もつクォークと「補色ほしょく」となるカラーチャージをもつ反はん粒子りゅうしとでペアを作つくる（メソン）か、3つのクォークについて3つの三原色さんげんしょくを重かさねて「白色はくしょく」となるようにトリオを作つくる（バリオン）かが考かんがえられる。SU(3) の表現ひょうげん論ろんの言葉ことばで言いえば、

3 × 3 = 1 + 8

3 × 3 × 3 = 1 + 8 + 8 + 10

に現あらわれる 1 がそれぞれメソンとバリオンに対応たいおうしている。グルーオンのみからも「白色はくしょく」の状態じょうたいを作つくることができる。そのような粒子りゅうしはグルーボールと呼よばれる。最もっとも簡単かんたんなグルーボールをSU(3) の表現ひょうげん論ろんの言葉ことばで言いえば、

8 × 8 = 1 + 8 + 8 + 10 + 10 + 27

に現あらわれる1が対応たいおうしている。また、これらの他ほかに「白色はくしょく」となる状態じょうたいの可能かのう性せいもあり、それらはエキゾチックであると呼よばれる。2003年ねんに報道ほうどうされたペンタクォークやテトラクォークはエキゾチックな粒子りゅうし（エキゾチックハドロン）の例れいである。 テトラクォークをSU(3) の表現ひょうげん論ろんの言葉ことばで言いえば、

3 × 3 × 3 × 3 = 1 + 8 + 8 + 10 + 8 + 10 + 1 + 8 + 27

に現あらわれる1が対応たいおうしている。

カラーチャージを持もつことは、強つよい相互そうご作用さようをするということと同おなじことである。それゆえ、電子でんしやニュートリノなどのレプトンや電磁でんじ相互そうご作用さようのゲージ粒子りゅうしである光子こうしはカラーチャージを持もっていない。

歴史れきし

強つよい相互そうご作用さようの現代げんだい的てきイメージの起源きげんはクォーク模型もけいである。1964年ねん、ゲルマンとツワイクによりクォークが導入どうにゅうされた。その後ご、クォークの束縛そくばく状態じょうたいであるハドロンのパウリ統計とうけいの問題もんだいから”新あたらしい”自由じゆう度ど、カラーがハン、南部なんぶ、グリーンバーグにより提唱ていしょうされた。一方いっぽうで、QCDの理論りろん的てき基礎きそは1954年ねんに発表はっぴょうされていた、ヤン＝ミルズの非ひ可か換かわゲージ理論りろんである。しかし、この理論りろんは質量しつりょうゼロのベクトル粒子りゅうし（つまり、長距離ちょうきょり相互そうご作用さようする粒子りゅうし）をふくみ、１fm以下いかのスケールの現象げんしょうの記述きじゅつを目指めざす理論りろんとしては不満足ふまんぞくなものだった。さらにこの当時とうじは非ひ可か換かわゲージ理論りろんの繰くり込こみ可能かのう性せいは証明しょうめいされていなかった。そして、南部なんぶはカイラル対称たいしょう性せいやその自発じはつ的てき対称たいしょう性せいの破やぶれなどを提唱ていしょうし、1970年代ねんだいに入はいると、非ひ可か換かわゲージ理論りろんの繰くり込こみ可能かのう性せいや漸近ぜんきん的てき自由じゆう性せいがようやく証明しょうめいされ、QCDは脚光きゃっこうを浴あびるようになる。

定式ていしき化か

数学すうがく的てきには、量子りょうし色しょく力学りきがく（以下いか、QCDと表記ひょうき）はSU(3)対称たいしょう群ぐんの非ひ可か換かわゲージ理論りろんである。カラーチャージを持もつディラック場じょう（クォーク場じょう）同士どうしの相互そうご作用さようを媒介ばいかいするゲージ場じょうはグルーオン場じょうである。

グルーオン場じょうと相互そうご作用さようするディラック場じょうについてのQCDラグランジアン密度みつどは以下いかのように表記ひょうきされる。

${\begin{aligned}{\mathcal {L}}_{\mathrm {QCD} }&={\bar {\psi }}_{i}\left(i\gamma ^{\mu }(D_{\mu })_{ij}-m\,\delta _{ij}\right)\psi _{j}-{\frac {1}{4}}G_{\mu \nu }^{a}G_{a}^{\mu \nu }\\&={\bar {\psi }}_{i}(i\gamma ^{\mu }\partial _{\mu }-m)\psi _{i}-g_{s}G_{\mu }^{a}{\bar {\psi }}_{i}\gamma ^{\mu }T_{ij}^{a}\psi _{j}-{\frac {1}{4}}G_{\mu \nu }^{a}G_{a}^{\mu \nu }\end{aligned}}$

ここで、

$\gamma ^{\mu }\,\!$ はガンマ行列ぎょうれつ

$\ \psi _{i}$ はカラーチャージ $\ i$ を持もつディラック場じょう（ただし、iは3成分せいぶん）

${\bar {\psi }}\equiv \psi ^{\dagger }\gamma _{0}$ はディラック場じょうの随伴ずいはんスピノル

$D_{\mu }=\partial _{\mu }+ig_{s}T^{a}G_{\mu }^{a}$ は共きょう変へん微分びぶん

$\ g_{s}$ はグルーオン場じょうの結合けつごう定数ていすう

$\ T^{a}$ はSU(3)の生成せいせい子こ（ただし、aは8成分せいぶん）

$\ G_{\mu }^{a}$ はグルーオン場じょう（電磁場でんじばにおける電磁でんじポテンシャルに相当そうとう）

$G_{\mu \nu }^{a}=\partial _{\mu }G_{\nu }^{a}-\partial _{\nu }G_{\mu }^{a}-g_{s}f^{abc}G_{\mu }^{b}G_{\nu }^{c}$ はグルーオン場じょうテンソル（電磁場でんじばにおける電磁場でんじばテンソルに相当そうとう）

$\ f^{abc}$ はSU(3)の構造こうぞう定数ていすう

である。

関連かんれん項目こうもく

• メソン - クォークと反はんクォークのペアからなるハドロン
• バリオン - クォーク3個こからなるハドロン
• ペンタクォーク - クォーク、反はんクォーク合あわせて5個こからなるハドロン
• テトラクォーク - クォーク、反はんクォーク合あわせて4個こからなるハドロン
• アキシオン
• 繰くり込こみ群ぐん
• ヤン・ミルズ理論りろん
• 格子こうしゲージ理論りろん