方 ほう 波 なみ 的 てき 傅 でん 里 さと 叶 かのう 前 まえ 随 ずい 着 ぎ 增加 ぞうか 更 さら 多 た 的 てき 部 ぶ 和 かず 收 おさむ 方 かた 波 は 在 ざい 数学 すうがく 中 なか 傅 でん 里 さと 叶 かのう 英語 えいご Fourier series ,是 これ 把 わ 波 なみ 的 てき 函数 かんすう 表示 ひょうじ 成 なり 谐波 的 てき 方式 ほうしき 更正 こうせい 式 しき 地 ち 狄利克 かつ 雷 かみなり 定理 ていり 的 てき 周期 しゅうき 函数 かんすう 里 さと 叶 かのう 级数 是 ぜ 由 よし 一 いち 正弦 せいげん 与 あずか 余弦 よげん 函数 かんすう 的 てき 加 か 和 わ 表示 ひょうじ 的 てき 方法 ほうほう 傅 でん 里 さと 叶 かのう 与 あずか 用 よう 来 らい 期 き 函数 かんすう 的 てき 信 しん 息 いき 的 てき 傅 でん 里 さと 叶 かのう 有 ゆう 密 みつ 切 きり 的 てき
傅 でん 里 さと 叶 かのう 是 ぜ 傅 でん 里 さと 叶 かのう 分析 ぶんせき 的 てき 一 いち 研究 けんきゅう 分 ぶん 支 ささえ 采 さい 定理 ていり 原始 げんし 的 てき 核心 かくしん 傅 でん 里 さと 叶 かのう 在 ざい 数 かず 组合数学 すうがく 、信号 しんごう 概 がい 率 りつ 统计学 がく 、密 みつ 声 こえ 学 がく 光学 こうがく 等 とう 都 と 有 ゆう 着 ぎ 的 てき
傅 でん 里 さと 叶 かのう 得 とく 名 めい 国 こく 数学 すうがく 家 か 约瑟夫 おっと 傅 でん 里 さと 叶 かのう (1768年 ねん 年 ねん 他 た 提出 ていしゅつ 任 にん 何 なに 函数 かんすう 都 と 可 か 展 てん 三角 さんかく 数学 すうがく 家 か 欧 おう 拉 ひしげ 达朗贝尔 和 わ 克 かつ 已 やめ 在 ざい 通 つう 分 ぶん 方法 ほうほう 数 すう 的 てき 公式 こうしき 拉 ひしげ 格 かく 朗 ろう 日 び 等 とう 人 ひと 已 やめ 了 りょう 将 はた 周期 しゅうき 函数 かんすう 分解 ぶんかい 振 ふ 函数 かんすう 的 てき 的 てき 最早 もはや 想 そう 法 ほう 可 か 溯 さかのぼ 至 いたり 公 こう 元 もと 前 まえ 世紀 せいき 古代 こだい 天文學 てんもんがく 家 か 的 てき 均 ひとし 輪 わ 和本 わほん 輪 わ 學說 がくせつ
傅 でん 里 さと 叶 かのう 的 てき 工作 こうさく 得 え 到 いた 了 りょう 丹 たん 尼 に 伯 はく 努 つとむ 利 り 的 てき [1] 傅 でん 里 さと 叶 かのう 介入 かいにゅう 热传导方程 ほど ,其最初 はつ 西 にし 拉 ひしげ 克 かつ 加 か 蒙 こうむ 日 ひ 同意 どうい [2] 但 ただし 在 ざい 年 ねん 拉 ひしげ 格 かく 朗 ろう 日 び 拉 ひしげ 普 ひろし 拉 ひしげ 和 わ 勒讓德 とく 评審后 きさき 被 ひ 拒 こばめ 出版 しゅっぱん 他 た 的 てき 被 ひ 称 しょう 傅 でん 里 さと 葉 は 逆轉 ぎゃくてん 定理 ていり 的 てき 理 り 来 らい 年 ねん 出版 しゅっぱん 的 てき 解析 かいせき 理 り [3]
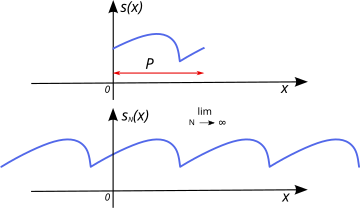
上 うえ 展示 てんじ 了 りょう 期 き 函数 かんすう
s
(
x
)
{\displaystyle s(x)}
定 てい 区 く
[
0
,
P
]
{\displaystyle [0,P]}
之 これ 上 じょう 可 か 里 さと 叶 かのう 是 ぜ 最初 さいしょ 函数 かんすう 的 てき 周期 しゅうき 延 のべ 拓 たく 的 てき 分析 ぶんせき 傅 でん 里 さと 叶 かのう 周期 しゅうき 函数 かんすう 即 そく 使 つかい 最初 さいしょ 函数 かんすう
s
(
x
)
{\displaystyle s(x)}
不 ふ 是 ぜ 周期 しゅうき 函数 かんすう 傅 でん 里 さと 叶 かのう 可 か 不同 ふどう 的 てき 形式 けいしき 来 き 表 おもて 下面 かめん 将 しょう 周期 しゅうき
P
{\displaystyle P}
的 てき 一 いち 周期 しゅうき 函數 かんすう
s
(
x
)
,
x
∈
R
{\textstyle s(x),\ x\in \mathbb {R} }
表 おもて 不同 ふどう 形式 けいしき 的 てき 傅 でん 里 さと 叶 かのう
人 ひと 常用 じょうよう
sin
(
x
)
{\displaystyle \sin(x)}
與 あずか
cos
(
x
)
{\displaystyle \cos(x)}
的 てき 三角 さんかく 級數 きゅうすう 來 らい 表示 ひょうじ
s
(
x
)
{\textstyle s(x)}
将 しょう 所有 しょゆう
n
{\displaystyle n}
階 かい 諧波
sin
(
2
π ぱい n
x
P
)
{\textstyle \sin({\frac {2\pi nx}{P}})}
與 あずか
cos
(
2
π ぱい n
x
P
)
{\textstyle \cos({\frac {2\pi nx}{P}})}
乘 じょう 各 かく 自在 じざい
s
(
x
)
{\textstyle s(x)}
中 なか 的 てき 權 けん 重 おも 求 もとめ 得 とく 的 てき 總和 そうわ
n
{\displaystyle n}
階 かい 的 てき 權 けん 重 じゅう 稱 しょう 爲 ため 傅 でん 立葉 たてば 級數 きゅうすう 係數 けいすう 可 か 由 よし 積分 せきぶん 來 らい 獲得 かくとく
傅 でん 立葉 たてば 級數 きゅうすう 係數 けいすう
A
0
=
1
P
∫
P
s
(
x
)
d
x
A
n
=
2
P
∫
P
s
(
x
)
cos
(
2
π ぱい n
x
P
)
d
x
for
n
≥
1
B
n
=
2
P
∫
P
s
(
x
)
sin
(
2
π ぱい n
x
P
)
d
x
for
n
≥
1
{\displaystyle {\begin{aligned}A_{0}&={\frac {1}{P}}\int _{P}s(x)\,dx\\A_{n}&={\frac {2}{P}}\int _{P}s(x)\cos \left({\frac {2\pi nx}{P}}\right)\,dx\qquad {\text{for }}n\geq 1\qquad \\B_{n}&={\frac {2}{P}}\int _{P}s(x)\sin \left({\frac {2\pi nx}{P}}\right)\,dx\qquad {\text{for }}n\geq 1\end{aligned}}}
Eq.1
符号 ふごう
∫
P
{\textstyle \int _{P}}
表示 ひょうじ 在 ざい 区 く 上 うえ 的 てき 典型 てんけい 的 てき
[
−
P
/
2
,
P
/
2
]
{\displaystyle [-P/2,P/2]}
或 ある 者 もの
[
0
,
P
]
{\displaystyle [0,P]}
注意 ちゅうい
A
0
{\displaystyle A_{0}}
是 ぜ 函数 かんすう
s
(
x
)
{\displaystyle s(x)}
的 てき 平均 へいきん [A] 性 せい 展 てん 到 いた 了 りょう 的 てき 比 ひ 傅 でん 里 さと 叶 かのう
通 つう 数 すう 定 てい 里 さと 叶 かのう
傅 でん 立葉 たてば 級數 きゅうすう ,
正弦 せいげん -
余弦 よげん 形式 けいしき
s
(
x
)
∼
A
0
+
∑
n
=
1
∞
(
A
n
cos
(
2
π ぱい n
x
P
)
+
B
n
sin
(
2
π ぱい n
x
P
)
)
{\displaystyle s(x)\sim A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left({\frac {2\pi nx}{P}}\right)+B_{n}\sin \left({\frac {2\pi nx}{P}}\right)\right)}
Eq.2
这里使用 しよう 符号 ふごう
∼
{\displaystyle \sim }
表示 ひょうじ 傅 でん 里 さと 叶 かのう 的 てき 求 もとめ 和 わ 不 ふ
s
(
x
)
{\displaystyle s(x)}
普遍 ふへん 來 らい 說 せつ
n
{\displaystyle n}
是 ぜ 理論 りろん 上 じょう 限 げん 大 だい 的 てき 但 ただし 是 ぜ 限 げん 大 だい 對 たい 所有 しょゆう 的 てき
x
{\displaystyle x}
例 れい 某 ぼう 一 いち 點 てん 上 じょう 不連續 ふれんぞく 傅 でん 立葉 たてば 級 きゅう 數也 かずや 不 ふ 一定 いってい 收斂 しゅうれん 到 いた
s
(
x
)
{\textstyle s(x)}
尽 つき 管 かん 不 ふ 收斂 しゅうれん 的 てき 可能 かのう 性 せい 始 はじめ 存在 そんざい 在 ざい 科学 かがく 和 わ 工程 こうてい 中 ちゅう 将 しょう Eq. 2 中 なか 的 てき
∼
{\displaystyle \sim }
直接 ちょくせつ 替 がえ 代 だい
=
{\displaystyle =}
在 ざい 傅 でん 里 さと 叶 かのう 系 けい 数 すう 中 ちゅう 的 てき 整数 せいすう 索引 さくいん
n
{\displaystyle n}
是 ぜ 中 ちゅう 相 しょう
cos
{\displaystyle \cos }
或 ある
sin
{\displaystyle \sin }
在 ざい 函数 かんすう 的 てき 周期 しゅうき
P
{\displaystyle P}
中 なか 形成 けいせい 的 てき 圆周 (cycle)的 てき 数 すう 目 もく 因 よし
A
n
{\displaystyle A_{n}}
和 わ
B
n
{\displaystyle B_{n}}
的 てき 着 ぎ
波 なみ 等 とう
P
n
{\displaystyle {\tfrac {P}{n}}}
有 ゆう 着 ぎ 同 どう
x
{\displaystyle x}
的 てき 频率 等 とう
n
P
{\displaystyle {\tfrac {n}{P}}}
有 ゆう 着 ぎ
x
{\displaystyle x}
的 てき 倒 たおせ 数 すう 下面 かめん 歐 おう 拉 ひしげ 公式 こうしき
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle \ e^{ix}=\cos x+i\sin x\ }
将 はた 傅 でん 里 さと 叶 かのう 系 けい 数 すう 化成 かせい 复数 指數 しすう 形式 けいしき
根據 こんきょ 定義 ていぎ 我 わが 到 いた
复数
傅 でん 里 さと 叶 かのう 级数
系 けい 数 すう
c
0
=
A
0
c
n
=
(
A
n
−
i
B
n
)
/
2
for
n
>
0
c
n
=
(
A
−
n
+
i
B
−
n
)
/
2
for
n
<
0
{\displaystyle {\begin{aligned}c_{0}&=A_{0}&\\c_{n}&=(A_{n}-iB_{n})/2\qquad &{\text{for }}n>0\\c_{n}&=(A_{-n}+iB_{-n})/2\qquad &{\text{for }}n<0\end{aligned}}}
Eq. 3
通 つう 等式 とうしき Eq. 1 代入 だいにゅう Eq. 3 可 か [4]
复数
傅 でん 里 さと 叶 かのう 级数
系 けい 数 すう
c
n
=
1
P
∫
P
s
(
x
)
e
−
2
π ぱい i
n
x
P
d
x
for
n
∈
Z
{\displaystyle c_{n}={\frac {1}{P}}\int _{P}s(x)e^{-{\frac {2\pi inx}{P}}}\,dx\qquad {\text{for}}\ n\in \mathbb {Z} }
给定复数傅 でん 里 さと 叶 かのう 系 けい 数 すう 可 か 公式 こうしき 出 で
A
n
{\displaystyle A_{n}}
和 わ
B
n
{\displaystyle B_{n}}
复数
傅 でん 里 さと 叶 かのう 级数
系 けい 数 すう
A
0
=
c
0
A
n
=
c
n
+
c
−
n
for
n
>
0
B
n
=
i
(
c
n
−
c
−
n
)
for
n
>
0
{\displaystyle {\begin{aligned}A_{0}&=c_{0}&\\A_{n}&=c_{n}+c_{-n}\qquad &{\textrm {for}}~n>0\\B_{n}&=i(c_{n}-c_{-n})\qquad &{\textrm {for}}~n>0\end{aligned}}}
通 つう 傅 でん 里 さと 叶 かのう 可 か
傅 でん 立葉 たてば 級數 きゅうすう ,
指數 しすう 形式 けいしき
s
(
x
)
∼
∑
n
=
−
∞
∞
c
n
⋅
e
2
π ぱい i
n
x
P
{\displaystyle s(x)\sim \sum _{n=-\infty }^{\infty }c_{n}\cdot e^{\frac {2\pi inx}{P}}}
Eq. 4
这是可 か 值域 函数 かんすう 的 てき 形式 けいしき
n
{\displaystyle n}
的 てき 负频率 りつ 。
人 ひと
s
(
x
)
{\textstyle s(x)}
的 てき 值域 普遍 ふへん 化 か 到 いた 複數 ふくすう 上 うえ
s
(
x
)
{\textstyle s(x)}
是 ぜ 一 いち 個 こ 複數 ふくすう 數 すう 實 み 部 ぶ 和 わ 虛 きょ 部 ぶ 都 みやこ 是 ただし 實數 じっすう 數 すう
s
(
x
)
=
Re
(
s
(
x
)
)
+
i
⋅
Im
(
s
(
x
)
)
,
x
∈
R
{\displaystyle s(x)=\operatorname {Re} (s(x))+i\cdot \operatorname {Im} (s(x)),\quad x\in \mathbb {R} }
定 てい
c
n
≜
c
R
n
+
i
⋅
c
I
n
{\displaystyle c_{n}\triangleq c_{_{Rn}}+i\cdot c_{_{In}}}
c
n
=
1
P
∫
P
s
(
x
)
⋅
e
−
i
2
π ぱい
p
n
x
d
x
=
1
P
∫
P
Re
(
s
(
x
)
)
⋅
e
−
i
2
π ぱい
p
n
x
d
x
+
i
⋅
1
P
∫
P
Im
(
s
(
x
)
)
⋅
e
−
i
2
π ぱい
p
n
x
d
x
{\displaystyle c_{n}={\frac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx={\frac {1}{P}}\int _{P}\operatorname {Re} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx+i\cdot {\frac {1}{P}}\int _{P}\operatorname {Im} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}
c
R
n
=
1
P
∫
P
Re
(
s
(
x
)
)
⋅
e
−
i
2
π ぱい
p
n
x
d
x
{\displaystyle c_{_{Rn}}={\frac {1}{P}}\int _{P}\operatorname {Re} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}
c
I
n
=
1
P
∫
P
Im
(
s
(
x
)
)
⋅
e
−
i
2
π ぱい
p
n
x
d
x
{\displaystyle c_{_{In}}={\frac {1}{P}}\int _{P}\operatorname {Im} (s(x))\cdot e^{-i{\tfrac {2\pi }{p}}nx}\ dx}
对于这个复数值函数 すう 傅 でん 里 さと 叶 かのう 的 てき 是 ぜ 的 てき 傅 でん 里 さと 叶 かのう 傅 でん 里 さと 叶 かのう 的 てき 虚 きょ 部 ぶ 是 ぜ 虚 きょ 部 ぶ 的 てき 傅 でん 里 さと 叶 かのう
s
(
x
)
∼
∑
n
=
−
∞
∞
(
c
R
n
+
i
⋅
c
I
n
)
⋅
e
i
2
π ぱい
p
n
x
=
∑
n
=
∞
∞
c
R
n
⋅
e
i
2
π ぱい
p
n
x
+
i
⋅
∑
n
=
−
∞
∞
c
I
n
⋅
e
i
2
π ぱい
p
n
x
{\displaystyle s(x)\sim \sum _{n=-\infty }^{\infty }\left(c_{_{Rn}}+i\cdot c_{_{In}}\right)\cdot e^{i{\tfrac {2\pi }{p}}nx}=\sum _{n=\infty }^{\infty }c_{_{Rn}}\cdot e^{i{\tfrac {2\pi }{p}}nx}+i\cdot \sum _{n=-\infty }^{\infty }c_{_{In}}\cdot e^{i{\tfrac {2\pi }{p}}nx}}
還 かえ 可 か 利用 りよう 三角 さんかく 恆等 こうとう 式 しき
cos
(
α あるふぁ −
β べーた )
=
cos
α あるふぁ cos
β べーた +
sin
α あるふぁ sin
β べーた
{\displaystyle \ \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta \,}
把 わ 正弦 せいげん 余弦 よげん 形式 けいしき 中後 なかご 面 めん 的 てき 正弦 せいげん 函數 かんすう 餘弦 よげん 函數 かんすう 合併 がっぺい 起 おこり 來 らい
A
n
⋅
cos
(
2
π ぱい
n
P
x
−
φ ふぁい
n
)
≡
A
n
cos
(
φ ふぁい
n
)
⏟
a
n
⋅
cos
(
2
π ぱい
n
P
x
)
+
A
n
sin
(
φ ふぁい
n
)
⏟
b
n
⋅
sin
(
2
π ぱい
n
P
x
)
{\displaystyle A_{n}\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)\ \equiv \ \underbrace {A_{n}\cos(\varphi _{n})} _{a_{n}}\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)+\underbrace {A_{n}\sin(\varphi _{n})} _{b_{n}}\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)}
然 しか 後 こう 定義 ていぎ 振幅 しんぷく
A
n
≜
a
n
2
+
b
n
2
{\textstyle A_{n}\triangleq {\sqrt {a_{n}^{2}+b_{n}^{2}}}}
相 そう 位 い
φ ふぁい
n
≜
arctan2
(
b
n
,
a
n
)
{\textstyle \varphi _{n}\triangleq \operatorname {arctan2} (b_{n},a_{n})}
的 てき
a
n
{\displaystyle a_{n}}
和 わ
b
n
{\displaystyle b_{n}}
正弦 せいげん 余弦 よげん 形式 けいしき 中 ちゅう
A
n
{\displaystyle A_{n}}
和 わ
B
n
{\displaystyle B_{n}}
A
0
2
{\displaystyle {\tfrac {A_{0}}{2}}}
是 これ
s
(
x
)
{\displaystyle s(x)}
的 てき 平均 へいきん
1
P
∫
P
s
(
x
)
d
x
{\textstyle {\frac {1}{P}}\int _{P}s(x)\,dx}
傅 でん 立葉 たてば 級數 きゅうすう ,
振幅 しんぷく -
相 そう 位 い 形式 けいしき
s
(
x
)
∼
A
0
2
+
∑
n
=
1
∞
A
n
⋅
cos
(
2
π ぱい
n
P
x
−
φ ふぁい
n
)
{\displaystyle s(x)\sim {\frac {A_{0}}{2}}+\sum _{n=1}^{\infty }A_{n}\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)}
Eq. 5
在 ざい 傅 でん 里 さと 叶 かのう 数 すう 行 ぎょう 会 かい 数 すう
f
(
x
)
{\displaystyle f(x)}
介入 かいにゅう 部 ぶ 和 わ 算 さん 子 こ
S
N
{\displaystyle S_{N}}
[5]
S
N
(
f
)
=
∑
n
=
−
N
N
c
n
e
2
π ぱい i
n
x
P
{\displaystyle S_{N}(f)=\sum _{n=-N}^{N}c_{n}e^{\frac {2\pi inx}{P}}}
Eq. 6
这里的 てき
c
n
{\displaystyle c_{n}}
是 これ
f
{\displaystyle f}
的 てき 傅 でん 里 さと 叶 かのう 系 けい 数 すう 不同 ふどう 中 ちゅう 的 てき 傅 でん 里 さと 叶 かのう 的 てき 部 ぶ 和 わ 采 さい 用 よう 形式 けいしき 否 いや 果 はて 可能 かのう 不成立 ふせいりつ
假設 かせつ
f
(
x
)
{\displaystyle f(x)}
與 あずか
g
(
x
)
{\displaystyle g(x)}
是 ぜ 在 ざい
R
{\textstyle \mathbb {R} }
上 うえ 的 てき 可 か 積 せき 函數 かんすう
f
(
x
)
{\displaystyle f(x)}
與 あずか
g
(
x
)
{\displaystyle g(x)}
在 ざい
[
−
π ぱい ,
π ぱい ]
{\displaystyle [-\pi ,\pi ]}
的 てき 捲 めく 積 せき
(
f
∗
g
)
(
x
)
{\displaystyle (f*g)(x)}
為 ため
(
f
∗
g
)
(
x
)
=
∫
−
π ぱい
π ぱい
f
(
τ たう )
g
(
x
−
τ たう )
d
τ たう
{\displaystyle (f*g)(x)=\int _{-\pi }^{\pi }f(\tau )g(x-\tau )d\tau }
周期 しゅうき
2
π ぱい
{\displaystyle 2\pi }
的 てき 函數 かんすう
f
(
x
)
{\displaystyle f(x)}
的 てき 傅 でん 立葉 たてば 級數 きゅうすう 的 てき 部 ぶ 和 わ 可 か 由 ゆかり
f
(
x
)
{\displaystyle f(x)}
与 あずか 狄利克 かつ 雷 かみなり 核 かく
D
n
(
x
)
=
∑
k
=
−
n
n
e
i
k
x
{\textstyle D_{n}(x)=\sum _{k=-n}^{n}e^{ikx}}
的 てき 摺 すり 積 せき 来 らい 表示 ひょうじ
S
N
(
f
)
(
x
)
=
∑
n
=
−
N
N
c
n
e
i
n
x
=
∑
n
=
−
N
N
(
1
2
π ぱい
∫
−
π ぱい
π ぱい
f
(
τ たう )
e
−
i
n
τ たう
d
τ たう
)
⋅
e
i
n
x
=
1
2
π ぱい
∫
−
π ぱい
π ぱい
f
(
τ たう )
(
∑
n
=
−
N
N
e
i
n
(
x
−
τ たう )
)
d
τ たう
=
1
2
π ぱい
(
f
∗
D
N
)
(
x
)
{\displaystyle {\begin{aligned}S_{N}(f)(x)&=\sum _{n=-N}^{N}c_{n}e^{inx}\\&=\sum _{n=-N}^{N}\left({\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(\tau )e^{-in\tau }d\tau \right)\cdot e^{inx}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(\tau )\left(\sum _{n=-N}^{N}e^{in(x-\tau )}\right)d\tau \\&={\frac {1}{2\pi }}(f*D_{N})(x)\end{aligned}}}
s
N
(
x
)
{\displaystyle s_{N}(x)}
在 ざい
[
x
0
,
x
0
+
P
]
{\displaystyle [x_{0},\ x_{0}+P]}
近似 きんじ 了 りょう
s
(
x
)
{\displaystyle s(x)}
近似 きんじ 程度 ていど 会 かい 随 ずい 着 ぎ
N
→
∞
{\displaystyle N\rightarrow \infty }
改善 かいぜん 无穷和 わ
s
∞
(
x
)
{\displaystyle s_{\infty }(x)}
叫 さけべ
s
{\displaystyle s}
的 てき 傅 でん 里 さと 叶 かのう 表示 ひょうじ 傅 でん 里 さと 叶 かのう 的 てき 收 おさむ 取 と 函数 かんすう 有限 ゆうげん 数量 すうりょう 的 てき 是 ぜ 通常 つうじょう 称 しょう 里 さと 叶 かのう 的 てき 狄利克 かつ 雷 かみなり 条件 じょうけん 。参 まいり 傅 でん 里 さと 叶 かのう 的 てき 收 おさむ 之 これ 一 いち 函数 かんすう 或 ある 分布 ぶんぷ 或 ある 弱 じゃく 收 おさむ 定 てい 里 さと 叶 かのう 系 けい 数 すう 在 ざい
s
(
x
)
{\displaystyle s(x)}
的 てき 不可 ふか 点 てん 上 じょう 我 わが 取 と 中 ちゅう 的 てき 有限 ゆうげん 和 わ 那 な 点 てん 上 じょう 会 かい 有 ゆう 幅 はば 度 ど 不随 ふずい
N
{\displaystyle N}
增大 ぞうだい 小 しょう 的 てき 起伏 きふく 吉 よし 布 ぬの 象 ぞう 方 ほう 波 なみ 信号 しんごう
在 ざい 工程 こうてい 中 ちゅう 原因 げんいん 是 ぜ 工程 こうてい 上 じょう 遇 ぐう 到 いた 的 てき 函数 かんすう 比 ひ 数学 すうがく 家 か 提供 ていきょう 的 てき 假定 かてい 的 てき 反例 はんれい 表 ひょう 加 か 良好 りょうこう 特 とく 傅 でん 里 さと 叶 かのう 绝对收 おさむ 且一 いち
s
(
x
)
{\displaystyle s(x)}
只 ただ 要 よう 在 ざい
s
(
x
)
{\displaystyle s(x)}
的 てき 或 ある 会 かい 存在 そんざい 是 ぜ 平方 へいほう 可 か [6]
[
x
0
,
x
0
+
P
]
{\displaystyle [x_{0},x_{0}+P]}
上 うえ 是 ただし 平方 へいほう 可 か 的 てき 那 な 傅 でん 里 さと 叶 かのう 在 ざい 几乎处处 的 まと 点 てん 都 みやこ 收 おさむ 数 すう
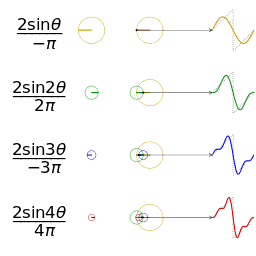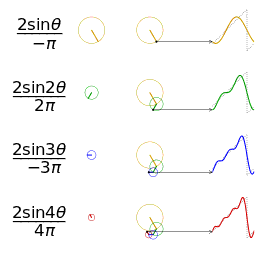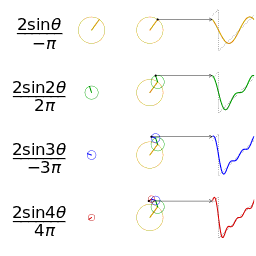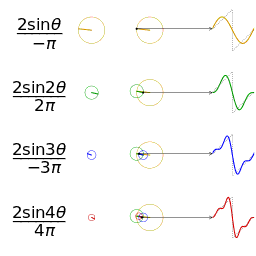
一个相同幅度和频率的锯齿波的近似的可视化
另一个分别采用傅里叶级数的前 1, 2, 3, 4 项
近似 きんじ 方 かた 波 なみ 的 てき 可 か 视化。(
可 か 以在这里
[7] 看 み 到 いた 一个交互式的动画)
收 おさむ 敛于
某 ぼう 个
任意 にんい 函数 かんすう 的 てき 例 れい 子 こ 。
注意 ちゅうい 其中
的 てき 吉 よし 布 ぬの 象 ぞう
符号 ふごう
c
n
{\displaystyle c_{n}}
在 ざい 多 た 同 どう 函数 かんすう 的 てき 傅 でん 里 さと 叶 かのう 系 けい 数 すう 不 ふ 的 てき 因 よし 将 はた 代 だい 数 すう 是 ぜ 函数 かんすう
s
{\displaystyle s}
的 てき 某 ぼう 改 あらため 形式 けいしき 即 そく 采 さい 用 よう 函数 かんすう 式 しき 符号 ふごう 比 ひ
s
^
[
n
]
{\displaystyle {\hat {s}}[n]}
或 ある
S
[
n
]
{\displaystyle S[n]}
来 らい 替 がえ 代 だい 下 か 符号 ふごう
s
(
x
)
=
∑
n
=
−
∞
∞
s
^
(
n
)
⋅
e
2
π ぱい i
n
x
/
P
{\displaystyle s(x)=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{2\pi inx/P}\quad }
常用 じょうよう 的 てき 数学 すうがく 符号 ふごう
s
(
x
)
=
∑
n
=
−
∞
∞
S
[
n
]
⋅
e
i
2
π ぱい n
x
/
P
{\displaystyle s(x)=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\quad }
常用 じょうよう 的 てき 工程 こうてい 符号 ふごう 在 ざい 工程 こうてい 上 じょう 特 とく 在 ざい
x
{\displaystyle x}
表示 ひょうじ 的 てき 系 けい 数 すう 序列 じょれつ 叫 さけべ 频域 表示 ひょうじ 使用 しよう 方 かた 括 くく 号 ごう 来 らい 强 きょう 数 すう 的 てき 定 てい 是 ぜ 频率 的 てき 集合 しゅうごう
另一个常用频域表示,使用 しよう 傅 でん 里 さと 叶 かのう 系 けい 数 すう 调制 像 ぞう 梳 くしけず 子 こ 一 いち 狄拉克 かつ 采 さい 数 すう
S
(
f
)
≜
∑
n
=
−
∞
∞
S
[
n
]
⋅
δ でるた
(
f
−
n
P
)
{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)}
这里的 てき
f
{\displaystyle f}
表示 ひょうじ 在 ざい
x
{\displaystyle x}
位 い 的 てき
f
{\displaystyle f}
赫兹 为单位 い 采 さい 基本 きほん
1
P
{\displaystyle {\tfrac {1}{P}}}
的 てき
n
{\displaystyle n}
倍 ばい 即 そく 谐波 )。
s
∞
(
x
)
{\displaystyle s_{\infty }(x)}
可 か 逆 ぎゃく 傅 でん 里 さと 叶 かのう 表示 ひょうじ 出来 でき
F
−
1
{
S
(
f
)
}
=
∫
−
∞
∞
(
∑
n
=
−
∞
∞
S
[
n
]
⋅
δ でるた
(
f
−
n
P
)
)
e
i
2
π ぱい f
x
d
f
=
∑
n
=
−
∞
∞
S
[
n
]
⋅
∫
−
∞
∞
δ でるた
(
f
−
n
P
)
e
i
2
π ぱい f
x
d
f
=
∑
n
=
−
∞
∞
S
[
n
]
⋅
e
i
2
π ぱい n
x
/
P
≜
s
∞
(
x
)
{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x)\end{aligned}}}
构造出 で 的 てき 函数 かんすう
S
(
f
)
{\displaystyle S(f)}
因 いん 通常 つうじょう 称 しょう 傅 でん 里 さと 叶 かのう 即 そく 使 つかい [B]
常用 じょうよう 的 てき 傅 でん 里 さと 叶 かのう [ 编辑 ] 下表 かひょう 列 れつ 出 で 常用 じょうよう 的 てき 周期 しゅうき 函数 かんすう 傅 でん 里 さと 叶 かのう 系 けい 数 すう
s
(
x
)
{\displaystyle s(x)}
指示 しじ 周期 しゅうき
P
{\displaystyle P}
的 てき 周期 しゅうき 函数 かんすう
A
0
{\displaystyle A_{0}}
A
n
{\displaystyle A_{n}}
和 わ
B
n
{\displaystyle B_{n}}
指示 しじ 周期 しゅうき 函数 かんすう
s
(
x
)
{\displaystyle s(x)}
的 てき 傅 でん 里 さと 叶 かのう 系 けい 数 すう 正弦 せいげん 余弦 よげん 形式 けいしき
时域
s
(
x
)
{\displaystyle s(x)}
绘图
频域(正弦 せいげん 余弦 よげん 形式 けいしき
A
0
A
n
for
n
≥
1
B
n
for
n
≥
1
{\displaystyle {\begin{aligned}&A_{0}\\&A_{n}\quad {\text{for }}n\geq 1\\&B_{n}\quad {\text{for }}n\geq 1\end{aligned}}}
注 ちゅう 引用 いんよう
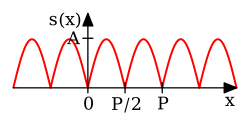
s
(
x
)
=
A
|
sin
(
2
π ぱい
P
x
)
|
for
0
≤
x
<
P
{\displaystyle s(x)=A\left|\sin \left({\frac {2\pi }{P}}x\right)\right|\quad {\text{for }}0\leq x<P}
A
0
=
2
A
π ぱい
A
n
=
{
−
4
A
π ぱい
1
n
2
−
1
n
even
0
n
odd
B
n
=
0
{\displaystyle {\begin{aligned}A_{0}=&{\frac {2A}{\pi }}\\A_{n}=&{\begin{cases}{\frac {-4A}{\pi }}{\frac {1}{n^{2}-1}}&\quad n{\text{ even}}\\0&\quad n{\text{ odd}}\end{cases}}\\B_{n}=&0\\\end{aligned}}}
全波 ぜんぱ 整流 せいりゅう 正弦 せいげん [8] :p. 193
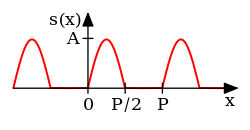
s
(
x
)
=
{
A
sin
(
2
π ぱい
P
x
)
for
0
≤
x
<
P
/
2
0
for
P
/
2
≤
x
<
P
{\displaystyle s(x)={\begin{cases}A\sin \left({\frac {2\pi }{P}}x\right)&\quad {\text{for }}0\leq x<P/2\\0&\quad {\text{for }}P/2\leq x<P\\\end{cases}}}
A
0
=
A
π ぱい
A
n
=
{
−
2
A
π ぱい
1
n
2
−
1
n
even
0
n
odd
B
n
=
{
A
2
n
=
1
0
n
>
1
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{\pi }}\\A_{n}=&{\begin{cases}{\frac {-2A}{\pi }}{\frac {1}{n^{2}-1}}&\quad n{\text{ even}}\\0&\quad n{\text{ odd}}\end{cases}}\\B_{n}=&{\begin{cases}{\frac {A}{2}}&\quad n=1\\0&\quad n>1\end{cases}}\\\end{aligned}}}
半 はん 波 なみ 整流 せいりゅう 正弦 せいげん [8] :p. 193
s
(
x
)
=
{
A
for
0
≤
x
<
D
⋅
P
0
for
D
⋅
P
≤
x
<
P
{\displaystyle s(x)={\begin{cases}A&\quad {\text{for }}0\leq x<D\cdot P\\0&\quad {\text{for }}D\cdot P\leq x<P\\\end{cases}}}
A
0
=
A
D
A
n
=
A
n
π ぱい
sin
(
2
π ぱい n
D
)
B
n
=
2
A
n
π ぱい
(
sin
(
π ぱい n
D
)
)
2
{\displaystyle {\begin{aligned}A_{0}=&AD\\A_{n}=&{\frac {A}{n\pi }}\sin \left(2\pi nD\right)\\B_{n}=&{\frac {2A}{n\pi }}\left(\sin \left(\pi nD\right)\right)^{2}\\\end{aligned}}}
0
≤
D
≤
1
{\displaystyle 0\leq D\leq 1}
s
(
x
)
=
A
x
P
for
0
≤
x
<
P
{\displaystyle s(x)={\frac {Ax}{P}}\quad {\text{for }}0\leq x<P}
A
0
=
A
2
A
n
=
0
B
n
=
−
A
n
π ぱい
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{2}}\\A_{n}=&0\\B_{n}=&{\frac {-A}{n\pi }}\\\end{aligned}}}
锯齿函数 かんすう
[8] :p. 192
s
(
x
)
=
A
−
A
x
P
for
0
≤
x
<
P
{\displaystyle s(x)=A-{\frac {Ax}{P}}\quad {\text{for }}0\leq x<P}
A
0
=
A
2
A
n
=
0
B
n
=
A
n
π ぱい
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{2}}\\A_{n}=&0\\B_{n}=&{\frac {A}{n\pi }}\\\end{aligned}}}
反 はん 函数 かんすう [8] :p. 192
s
(
x
)
=
4
A
P
2
(
x
−
P
2
)
2
for
0
≤
x
<
P
{\displaystyle s(x)={\frac {4A}{P^{2}}}\left(x-{\frac {P}{2}}\right)^{2}\quad {\text{for }}0\leq x<P}
A
0
=
A
3
A
n
=
4
A
π ぱい
2
n
2
B
n
=
0
{\displaystyle {\begin{aligned}A_{0}=&{\frac {A}{3}}\\A_{n}=&{\frac {4A}{\pi ^{2}n^{2}}}\\B_{n}=&0\\\end{aligned}}}
反 はん 全波 ぜんぱ 整流 せいりゅう [8] :p. 193
下表 かひょう 展示 てんじ 在 ざい 中 ちゅう 的 てき
复数共 ども 指示 しじ 号 ごう
∗
{\displaystyle \ ^{*}\ }
s
(
x
)
{\displaystyle s(x)}
和 わ
r
(
x
)
{\displaystyle r(x)}
指示 しじ 周期 しゅうき
P
{\displaystyle P}
的 てき 函数 かんすう 或 ある 只 ただ 定 てい
x
∈
[
0
,
P
]
{\displaystyle x\in [0,P]}
中 なか 的 てき 函数 かんすう
S
[
n
]
{\displaystyle S[n]}
和 わ
R
[
n
]
{\displaystyle R[n]}
指示 しじ
s
{\displaystyle s}
和 わ
r
{\displaystyle r}
的 てき 傅 でん 里 さと 叶 かのう 系 けい 数 すう 指数 しすう 形式 けいしき
性 せい 时域
频域(指数 しすう 形式 けいしき
注 ちゅう 引用 いんよう
线性
a
⋅
s
(
x
)
+
b
⋅
r
(
x
)
{\displaystyle a\cdot s(x)+b\cdot r(x)}
a
⋅
S
[
n
]
+
b
⋅
R
[
n
]
{\displaystyle a\cdot S[n]+b\cdot R[n]}
a
,
b
∈
C
{\displaystyle a,b\in \mathbb {C} }
时间反 はん 反 はん
s
(
−
x
)
{\displaystyle s(-x)}
S
[
−
n
]
{\displaystyle S[-n]}
[9] :p. 610
时间共 ども
s
∗
(
x
)
{\displaystyle s^{*}(x)}
S
∗
[
−
n
]
{\displaystyle S^{*}[-n]}
[9] :p. 610
时间反 はん 共 ども
s
∗
(
−
x
)
{\displaystyle s^{*}(-x)}
S
∗
[
n
]
{\displaystyle S^{*}[n]}
时间实部
Re
(
s
(
x
)
)
{\displaystyle \operatorname {Re} {(s(x))}}
1
2
(
S
[
n
]
+
S
∗
[
−
n
]
)
{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}
时间虚 きょ 部 ぶ
Im
(
s
(
x
)
)
{\displaystyle \operatorname {Im} {(s(x))}}
1
2
i
(
S
[
n
]
−
S
∗
[
−
n
]
)
{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}
频率实部
1
2
(
s
(
x
)
+
s
∗
(
−
x
)
)
{\displaystyle {\frac {1}{2}}(s(x)+s^{*}(-x))}
Re
(
S
[
n
]
)
{\displaystyle \operatorname {Re} {(S[n])}}
频率虚 きょ 部 ぶ
1
2
i
(
s
(
x
)
−
s
∗
(
−
x
)
)
{\displaystyle {\frac {1}{2i}}(s(x)-s^{*}(-x))}
Im
(
S
[
n
]
)
{\displaystyle \operatorname {Im} {(S[n])}}
时间移 うつり 位 い
s
(
x
−
x
0
)
{\displaystyle s(x-x_{0})}
S
[
n
]
⋅
e
−
i
2
π ぱい
P
n
x
0
{\displaystyle S[n]\cdot e^{-i{\frac {2\pi }{P}}nx_{0}}}
x
0
∈
R
{\displaystyle x_{0}\in \mathbb {R} }
[9] :p. 610
频率移 うつり 位 い
s
(
x
)
⋅
e
i
2
π ぱい
P
n
0
x
{\displaystyle s(x)\cdot e^{i{\frac {2\pi }{P}}n_{0}x}}
S
[
n
−
n
0
]
{\displaystyle S[n-n_{0}]\!}
n
0
∈
Z
{\displaystyle n_{0}\in \mathbb {Z} }
[9] :p. 610
所有 しょゆう 的 てき 函数 かんすう 都 と 可 か 分解 ぶんかい 成 なり 唯一 ゆいいつ 性的 せいてき 偶部和 わ 奇 き 部 ぶ
f
(
x
)
=
f
e
(
x
)
+
f
o
(
x
)
{\displaystyle f(x)=f_{\text{e}}(x)+f_{\text{o}}(x)}
的 てき
f
e
(
x
)
=
f
(
x
)
+
f
(
−
x
)
2
{\textstyle f_{\text{e}}(x)={\frac {f(x)+f(-x)}{2}}}
f
o
(
x
)
=
f
(
x
)
−
f
(
−
x
)
2
{\textstyle f_{\text{o}}(x)={\frac {f(x)-f(-x)}{2}}}
参 さん 数 すう 的 てき 数 すう
f
:
R
→
C
{\displaystyle f:\mathbb {R} \to \mathbb {C} }
所有 しょゆう
x
∈
R
{\displaystyle x\in \mathbb {R} }
f
(
x
)
=
f
(
−
x
)
¯
{\displaystyle f(x)={\overline {f(-x)}}}
称 しょう
f
(
x
)
=
−
f
(
−
x
)
¯
{\displaystyle f(x)=-{\overline {f(-x)}}}
奇 き
z
¯
{\displaystyle {\overline {z}}}
的 てき 上 じょう 指示 しじ 复数共 ども 。
一个复数值函数的实部和虚部,分解 ぶんかい 成 なり 各自 かくじ 的 てき 和 わ 奇 き 部 ぶ 了 りょう 四 よん 量 りょう 分 ふん 下 か 明 あかり 和 わ 与 あずか 的 てき 有 ゆう 着 ぎ 一 いち 一 いち 映 うつ 射 い [10]
时 域 いき
s
=
s
RE
+
s
RO
+
i
s
IE
+
i
s
IO
⇕
F
⇕
F
⇕
F
⇕
F
⇕
F
频 域 いき
S
=
S
RE
+
i
S
IO
+
i
S
IE
+
S
RO
{\displaystyle {\begin{array}{rccccccccc}{\text{时 域 いき 域 いき
由 よし 各 かく 系 けい 是 ぜ 易 えき 例 れい
实数值函数 すう s RE s RO 的 てき 是 ぜ 称 しょう 函数 かんすう S RE i S IO 反 はん 称 しょう 了 りょう 域 いき
虚数 きょすう 数 すう i s IE i s IO 的 てき 是 ぜ 奇 き 函数 かんすう S RO i S IE 反 はん 成立 せいりつ 偶对称 しょう 函数 かんすう s RE i s IO 的 てき 是 ぜ 数 すう S RE S RO 反 はん 成立 せいりつ
奇 き 函数 かんすう s RO i s IE 的 てき 是 ぜ 虚数 きょすう 数 すう i S IE i S IO 反 はん 成立 せいりつ 锯齿波 は 周期 しゅうき 函数 かんすう 的 てき 前 ぜん 我 わが 在 ざい 用 よう 上面 うわつら 的 てき 公式 こうしき 考 こう
s
(
x
)
=
x
π ぱい
,
f
o
r
−
π ぱい <
x
<
π ぱい
{\displaystyle s(x)={\frac {x}{\pi }},\quad \mathrm {for} -\pi <x<\pi }
s
(
x
+
2
π ぱい k
)
=
s
(
x
)
,
f
o
r
−
∞
<
x
<
∞
and
k
∈
Z
{\displaystyle s(x+2\pi k)=s(x),\quad \mathrm {for} -\infty <x<\infty {\text{ and }}k\in \mathbb {Z} }
在 ざい 情 じょう 傅 でん 里 さと 叶 かのう
A
n
=
1
π ぱい
∫
−
π ぱい
π ぱい
s
(
x
)
cos
(
n
x
)
d
x
=
0
,
n
≥
0
B
n
=
1
π ぱい
∫
−
π ぱい
π ぱい
s
(
x
)
sin
(
n
x
)
d
x
=
−
2
π ぱい n
cos
(
n
π ぱい )
+
2
π ぱい
2
n
2
sin
(
n
π ぱい )
=
2
(
−
1
)
n
+
1
π ぱい n
,
n
≥
1
{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1\end{aligned}}}
可 か 明 あきら 当 とう
s
{\displaystyle s}
可 か 微 ほろ 傅 でん 立 たて 叶 かのう 在 ざい 每 まい
x
{\displaystyle x}
都 みやこ 收 おさむ
s
(
x
)
{\displaystyle s(x)}
s
(
x
)
=
A
0
+
∑
n
=
1
∞
(
A
n
cos
(
n
x
)
+
B
n
sin
(
n
x
)
)
=
2
π ぱい
∑
n
=
1
∞
(
−
1
)
n
+
1
n
sin
(
n
x
)
,
f
o
r
x
−
π ぱい ∉
2
π ぱい
Z
{\displaystyle {\begin{aligned}s(x)&=A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left(nx\right)+B_{n}\sin \left(nx\right)\right)\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} \end{aligned}}}
Eq.1
当 とう
x
=
π ぱい
{\displaystyle x=\pi }
傅 でん 里 さと 叶 かのう 收 おさむ
0
{\displaystyle 0}
x
=
π ぱい
{\displaystyle x=\pi }
s
{\displaystyle s}
的 てき 左 ひだり 和 わ 右 みぎ 之 の 和 わ 的 てき 一半 いっぱん 傅 でん 里 さと 叶 かのう 的 てき 狄利克 かつ 雷 かみなり 定理 ていり 的 てき 特例 とくれい
这个例 れい 子 こ 出 で 了 りょう 巴 ともえ 塞 ふさが 的 てき 一 いち 法 ほう
金属 きんぞく 板 いた 内 ない 的 てき 分布 ぶんぷ 使用 しよう 傅 でん 里 さと 叶 かのう 方法 ほうほう 求 もとめ 解 かい 在 ざい 上 うえ 例 れい 中 ちゅう 我 わが 函数 かんすう 的 てき 傅 でん 里 さと 叶 かのう 展 てん 看 み 起 おこり 来 き 不 ふ 比 ひ
s
(
x
)
=
x
π ぱい
{\displaystyle s(x)={\tfrac {x}{\pi }}}
因 いん 要 よう 傅 でん 里 さと 叶 かのう 的 てき 原因 げんいん 不 ふ 会 かい 立 りつ 即 そく 出来 でき 但 ただし 我 わが 用 よう 傅 でん 里 さと 叶 かのう 解 かい 热方程 ほど 的 てき 例 れい 子 こ 考 こう
π ぱい
{\displaystyle \pi }
米 べい 的 てき 方形 ほうけい 金属 きんぞく 版 ばん 坐 すわ
(
x
,
y
)
∈
[
0
,
π ぱい ]
×
[
0
,
π ぱい ]
{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}
板 いた 内 ない 没 ぼつ 有 ゆう
0
{\displaystyle 0}
度 ど 四 よん 条 じょう
y
=
π ぱい
{\displaystyle y=\pi }
x
∈
(
0
,
π ぱい )
{\displaystyle x\in (0,\pi )}
保持 ほじ 在 ざい 温度 おんど 梯 はしご 度 ど
T
(
x
,
π ぱい )
=
x
{\displaystyle T(x,\pi )=x}
度 ど 在 ざい 情 じょう 或 ある 者 もの 后 きさき 的 てき 分布 ぶんぷ 函数 かんすう
T
(
x
,
y
)
{\displaystyle T(x,y)}
不能 ふのう 得 とく 出 で 解析 かいせき 解 かい 但 ただし 明 あきら
T
(
x
,
y
)
=
2
∑
n
=
1
∞
(
−
1
)
n
+
1
n
sin
(
n
x
)
sinh
(
n
y
)
sinh
(
n
π ぱい )
{\displaystyle T(x,y)=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx){\sinh(ny) \over \sinh(n\pi )}}
这里的 てき
sinh
{\displaystyle \sinh }
是 これ 双 そう 曲 きょく 正弦 せいげん 函数 かんすう 程 ほど 的 てき 解 かい 是 ぜ 通 どおり
π ぱい s
(
x
)
{\displaystyle \pi s(x)}
的 てき 傅 でん 里 さと 叶 かのう 的 てき 每 ごと 一 いち
sinh
(
n
y
)
sinh
(
n
π ぱい )
{\displaystyle {\tfrac {\sinh(ny)}{\sinh(n\pi )}}}
得 え 到 いた 的 てき 尽 つき 管 かん 示 しめせ 例 れい 的 てき 函数 かんすう
s
(
x
)
{\displaystyle s(x)}
的 てき 傅 でん 里 さと 叶 かのう 似 に 用 よう 傅 でん 里 さと 叶 かのう 的 てき 方法 ほうほう 解 かい 分布 ぶんぷ
我 わが 可 か 應用 おうよう 傅 でん 立葉 たてば 級數 きゅうすう 去 さ 證明 しょうめい 等 とう 周 しゅう 不等式 ふとうしき 或 ある 是 ぜ 構造 こうぞう 處處 しょしょ 連續 れんぞく 處處 しょしょ 不可 ふか 微 ほろ 的 てき 函數 かんすう
至 いたり 今 こん 有 ゆう 判断 はんだん 傅 でん 里 さと 叶 かのう 的 てき 收 おさむ 充分 じゅうぶん 必要 ひつよう 条件 じょうけん 但 ただし 是 ぜ 中出 なかいで 函数 かんすう 有 ゆう 条件 じょうけん 可用 かよう 判断 はんだん 收 おさむ 比 ひ
x
(
t
)
{\displaystyle x(t)}
的 まと 可 か 微 ほろ 性 せい 或 ある 的 てき 一 いち 在 ざい 狄利克 かつ 雷 かみなり 条件 じょうけん 的 てき 函数 かんすう 表示 ひょうじ 成 なり 的 てき 傅 でん 里 さと 叶 かのう 都 みやこ 收 おさむ 克 かつ 雷 かみなり 条件 じょうけん
在 ざい 定 てい
x
(
t
)
{\displaystyle x(t)}
绝对可 か ;在任 ざいにん 一 いち 有限 ゆうげん 区 く
x
(
t
)
{\displaystyle x(t)}
只 ただ 能取 のとろ 有限 ゆうげん 在任 ざいにん 何 なん 有限 ゆうげん 区 く
x
(
t
)
{\displaystyle x(t)}
只 ただ 能 のう 有 ゆう 有限 ゆうげん 第 だい 一 いち 断 だん 点 てん 满足以上 いじょう 条件 じょうけん 的 てき
x
(
t
)
{\displaystyle x(t)}
傅 でん 里 さと 叶 かのう 都 みやこ 收 おさむ
1.当 とう
t
{\displaystyle t}
是 これ
x
(
t
)
{\displaystyle x(t)}
的 てき 点 てん 收 おさむ
x
(
t
)
{\displaystyle x(t)}
2.当 とう
t
{\displaystyle t}
是 これ
x
(
t
)
{\displaystyle x(t)}
的 てき 点 てん 收 おさむ
1
2
[
x
(
t
−
)
+
x
(
t
+
)
]
{\displaystyle {\frac {1}{2}}[x(t^{-})+x(t^{+})]}
1966年 ねん 里 さと 松 まつ 了 りょう 勒贝格 かく 二 に 次 じ 可 か 函数 かんすう 的 てき 傅 でん 立 たて 叶 かのう 即 そく 在 ざい 除 じょ 了 りょう
傅 でん 立葉 たてば 級數 きゅうすう 收斂 しゅうれん [ 编辑 ] 假設 かせつ 一 いち 個 こ 函數 かんすう 在 ざい
f
(
x
)
{\displaystyle f(x)}
在 ざい
[
0
,
2
π ぱい ]
{\displaystyle [0,2\pi ]}
上 うえ 是 ただし 平方 へいほう 可 か 積 せき 則 のり 會 かい 有 ゆう
1
2
π ぱい
∫
0
2
π ぱい
|
f
(
x
)
−
S
N
(
f
)
(
x
)
|
2
d
x
→
0
{\displaystyle {\frac {1}{2\pi }}\int _{0}^{2\pi }|f(x)-S_{N}(f)(x)|^{2}dx\rightarrow 0}
當 とう
N
→
∞
{\displaystyle N\rightarrow \infty }
證明 しょうめい 的 てき 第一步 だいいっぽ
考慮 こうりょ 一 いち 系列 けいれつ 正 せい 底 そこ
{
e
n
}
n
∈
Z
{\displaystyle \{e_{n}\}_{n\in \mathbb {Z} }}
e
n
(
x
)
=
e
−
i
n
x
{\displaystyle e_{n}(x)=e^{-inx}}
(
e
n
,
e
m
)
=
{
1
,
if
n
=
m
0
,
if
n
≠
m
{\displaystyle (e_{n},e_{m})={\begin{cases}1,&{\text{if }}n=m\\0,&{\text{if }}n\neq m\end{cases}}}
然 しか 後 こう 有 ゆう
(
f
,
e
n
)
=
1
2
π ぱい
∫
0
2
π ぱい
f
(
x
)
e
−
i
n
x
d
x
=
f
^
(
n
)
{\displaystyle (f,e_{n})={\frac {1}{2\pi }}\int _{0}^{2\pi }f(x)e^{-inx}dx={\hat {f}}(n)}
特別 とくべつ 的 てき 有 ゆう
f
(
x
)
{\displaystyle f(x)}
的 てき 傅 でん 立葉 たてば 級數 きゅうすう 的 てき 部分 ぶぶん 和 わ
S
N
(
f
)
(
x
)
=
∑
|
n
|
≤
N
f
^
(
n
)
e
n
{\displaystyle S_{N}(f)(x)=\sum _{|n|\leq N}{\hat {f}}(n)e_{n}}
然 しか 後 こう 根據 こんきょ
f
=
f
−
∑
|
n
|
≤
N
f
^
(
n
)
e
n
+
∑
|
n
|
≤
N
f
^
(
n
)
e
n
{\displaystyle f=f-\sum _{|n|\leq N}{\hat {f}}(n)e_{n}+\sum _{|n|\leq N}{\hat {f}}(n)e_{n}}
定理 ていり 可 か
|
|
f
|
|
2
=
|
|
f
−
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
+
|
|
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
{\displaystyle ||f||^{2}=||f-\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}+||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}}
替 かえ 換 かわ 一 いち 下 か 後 ご 有 ゆう
|
|
f
|
|
2
=
|
|
f
−
S
N
(
f
)
(
x
)
|
|
2
+
|
|
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
{\displaystyle ||f||^{2}=||f-S_{N}(f)(x)||^{2}+||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}}
如果右邊 うへん 第 だい 一 いち 項 こう 收斂 しゅうれん 到 いた 再 さい 根據 こんきょ 正 せい 性質 せいしつ 可 か 出 で 上述 じょうじゅつ 式 しき 子中 こなか 的 てき 右手 みぎて 邊 べ 第 だい 二 に 項 こう
|
|
∑
|
n
|
≤
N
f
^
(
n
)
e
n
|
|
2
=
∑
|
n
|
≤
N
|
f
^
(
n
)
|
2
{\displaystyle ||\sum _{|n|\leq N}{\hat {f}}(n)e_{n}||^{2}=\sum _{|n|\leq N}|{\hat {f}}(n)|^{2}}
證明 しょうめい 了 りょう 帕塞瓦 かわら 定理 ていり 。证明的 てき 第 だい 二 に 步 ほ
回 かい 到 いた 證明 しょうめい 右邊 うへん 第 だい 一 いち 項 こう 因 いん 為 ため 函數 かんすう
f
(
x
)
{\displaystyle f(x)}
可 か 積 せき 一 いち 個 こ 連續 れんぞく 函數 かんすう
g
(
x
)
{\displaystyle g(x)}
然 しか 後 こう 根據 こんきょ 最 さい 佳 けい 可 か 一 いち 個 こ 三 さん 角 かく 多項式 たこうしき 使 つかい 得 とく
|
f
−
S
N
(
f
)
(
x
)
|
≤
|
f
(
x
)
−
g
(
x
)
|
+
|
g
(
x
)
−
S
N
(
f
)
(
x
)
|
{\displaystyle |f-S_{N}(f)(x)|\leq |f(x)-g(x)|+|g(x)-S_{N}(f)(x)|}
故 こ 當 とう
N
→
∞
{\displaystyle N\rightarrow \infty }
函數 かんすう
f
(
x
)
{\displaystyle f(x)}
S
N
(
f
)
(
x
)
{\displaystyle S_{N}(f)(x)}
的 まと 差 さ 為 ため
傅 でん 立葉 たてば 級數 きゅうすう 的 てき 唯 ただ 一 いち 性 せい [ 编辑 ] 如果有 ゆう 一 いち 個 こ 定義 ていぎ 在 ざい
[
−
π ぱい ,
π ぱい ]
{\displaystyle [-\pi ,\pi ]}
的 てき 函數 かんすう
f
(
x
)
{\displaystyle f(x)}
和 わ
g
(
x
)
{\displaystyle g(x)}
函數 かんすう
f
(
x
)
{\displaystyle f(x)}
和 わ
g
(
x
)
{\displaystyle g(x)}
的 てき 傅 でん 立葉 たてば 係數 けいすう
f
^
(
n
)
{\displaystyle {\hat {f}}(n)}
還 かえ 有 ゆう
g
^
(
n
)
{\displaystyle {\hat {g}}(n)}
相 あい 同 どう 立葉 たてば 級數 きゅうすう 都 と 收斂 しゅうれん 到 いた 函數 かんすう 本身 ほんみ 那 な 證明 しょうめい 立葉 たてば 級數 きゅうすう 具有 ぐゆう 唯一 ゆいいつ 性 せい 是 ぜ
f
(
x
)
=
g
(
x
)
{\displaystyle f(x)=g(x)}
換 かわ 句 く 話 はなし 說 せつ 函數 かんすう
f
(
x
)
{\displaystyle f(x)}
在 ざい
[
−
π ぱい ,
π ぱい ]
{\displaystyle [-\pi ,\pi ]}
上 うえ 可 か 積 せき 傅 でん 立葉 たてば 係數 けいすう
f
^
(
n
)
{\displaystyle {\hat {f}}(n)}
為 ため 對 たい 所有 しょゆう 的 てき
n
∈
N
{\displaystyle n\in \mathbb {N} }
那 な 數 すう
f
(
x
)
=
0
{\displaystyle f(x)=0}
给定周期 しゅうき
P
{\displaystyle P}
的 てき 函数 かんすう
s
P
{\displaystyle s_{_{P}}}
和 わ
r
P
{\displaystyle r_{_{P}}}
具有 ぐゆう 傅 でん 里 さと 叶 かのう 系 けい 数 すう
S
[
n
]
{\displaystyle S[n]}
和 わ
R
[
n
]
{\displaystyle R[n]}
的 てき
n
∈
Z
{\displaystyle n\in \mathbb {Z} }
逐点乘 じょう
h
P
(
x
)
≜
s
P
(
x
)
⋅
r
P
(
x
)
{\displaystyle h_{_{P}}(x)\triangleq s_{_{P}}(x)\cdot r_{_{P}}(x)}
周期 しゅうき
P
{\displaystyle P}
傅 でん 里 さと 叶 かのう 系 けい 数 すう 是 ぜ 序列 じょれつ
S
{\displaystyle S}
和 わ
R
{\displaystyle R}
的 てき 离散卷 まき :
H
[
n
]
=
(
S
∗
R
)
[
n
]
{\displaystyle H[n]=(S*R)[n]}
周期 しゅうき 卷 まき
h
P
(
x
)
≜
(
s
P
∗
r
)
(
x
)
=
(
s
∗
r
P
)
(
x
)
=
∫
P
s
P
(
τ たう )
⋅
r
P
(
x
−
τ たう )
d
τ たう
{\textstyle h_{_{P}}(x)\triangleq (s_{_{P}}*r)(x)=(s*r_{_{P}})(x)=\int _{P}s_{_{P}}(\tau )\cdot r_{_{P}}(x-\tau )\,d\tau }
周期 しゅうき
P
{\displaystyle P}
具有 ぐゆう 傅 でん 里 さと 叶 かのう 系 けい 数 すう
H
[
n
]
=
P
⋅
S
[
n
]
⋅
R
[
n
]
{\displaystyle H[n]=P\cdot S[n]\cdot R[n]}
在 ざい
c
0
(
Z
)
{\displaystyle c_{0}(\mathbb {Z} )}
中 なか 的 てき 双 そう 序列 じょれつ
{
c
n
}
n
∈
Z
{\displaystyle \left\{c_{n}\right\}_{n\in Z}}
是 ぜ 在 ざい
L
1
(
[
0
,
2
π ぱい ]
)
{\displaystyle L^{1}([0,2\pi ])}
中 なか 的 てき 傅 でん 里 さと 叶 かのう 系 けい 数 すう 的 てき 序列 じょれつ 当 とう 当 とう 在 ざい
ℓ
2
(
Z
)
{\displaystyle \ell ^{2}(\mathbb {Z} )}
中 なか 的 てき 序列 じょれつ 的 てき 卷 まき [11] 我 わが
f
(
x
)
{\displaystyle f(x)}
屬 ぞく
C
k
(
T
)
{\displaystyle C^{k}(\mathbb {T} )}
⇒
{\displaystyle \Rightarrow }
f
(
x
)
{\displaystyle f(x)}
是 ぜ
2
π ぱい
{\displaystyle 2\pi }
為 ため 週 しゅう 期 き 的 てき 函數 かんすう
k
{\displaystyle k}
次 つぎ 可 か 微 ほろ
k
{\displaystyle k}
階 かい 連續 れんぞく
如果
f
(
x
)
{\displaystyle f(x)}
屬 ぞく
C
1
(
T
)
{\displaystyle C^{1}(\mathbb {T} )}
那 な
f
′
(
x
)
{\displaystyle f'(x)}
傅 でん 立葉 たてば 係數 けいすう
f
′
^
(
n
)
{\displaystyle {\hat {f'}}(n)}
可 か 用 よう
f
(
x
)
{\displaystyle f(x)}
傅 でん 立葉 たてば 係數 けいすう
f
^
(
n
)
{\displaystyle {\hat {f}}(n)}
的 てき 表示 ひょうじ 公式 こうしき
f
′
^
(
n
)
=
i
n
f
^
(
n
)
{\displaystyle {\hat {f'}}(n)=in{\hat {f}}(n)}
如果
f
(
x
)
{\displaystyle f(x)}
屬 ぞく
C
k
(
T
)
{\displaystyle C^{k}(\mathbb {T} )}
f
(
k
)
^
(
n
)
=
(
i
n
)
k
f
^
(
n
)
{\displaystyle {\hat {f^{(k)}}}(n)=(in)^{k}{\hat {f}}(n)}
特別 とくべつ 的 てき 當 とう 固定 こてい
k
≥
1
{\displaystyle k\geq 1}
我 わが
f
(
k
)
^
(
n
)
{\displaystyle {\hat {f^{(k)}}}(n)}
當 とう
n
→
∞
{\displaystyle n\rightarrow \infty }
f
(
k
)
^
(
n
)
=
O
(
1
/
n
k
)
{\displaystyle {\hat {f^{(k)}}}(n)=O(1/n^{k})}
如果
S
{\displaystyle S}
是 これ 可 か 数 すう
lim
|
n
|
→
∞
S
[
n
]
=
0
{\textstyle \lim _{|n|\to \infty }S[n]=0}
lim
n
→
+
∞
a
n
=
0
{\textstyle \lim _{n\to +\infty }a_{n}=0}
lim
n
→
+
∞
b
n
=
0
{\textstyle \lim _{n\to +\infty }b_{n}=0}
如果函數 かんすう
f
(
x
)
{\displaystyle f(x)}
屬 ぞく
L
2
(
[
−
π ぱい ,
π ぱい ]
)
{\displaystyle L^{2}([-\pi ,\pi ])}
之 これ 中 ちゅう 那 な 有 ゆう
∑
−
∞
∞
|
f
^
(
n
)
|
2
=
1
2
π ぱい
∫
−
π ぱい
π ぱい
|
f
(
x
)
|
2
d
x
=
|
|
f
|
|
{\textstyle \sum _{-\infty }^{\infty }|{\hat {f}}(n)|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}dx=||f||}
如果
c
0
,
c
±
1
,
c
±
2
,
…
{\displaystyle c_{0},\,c_{\pm 1},\,c_{\pm 2},\ldots }
是 ぜ 系 けい 数 すう
∑
n
=
−
∞
∞
|
c
n
|
2
<
∞
{\textstyle \sum _{n=-\infty }^{\infty }|c_{n}|^{2}<\infty }
一 いち 一 いち 的 てき 函数 かんすう
s
∈
L
2
(
P
)
{\displaystyle s\in L^{2}(P)}
使 つかい 得 とく 所有 しょゆう
n
{\displaystyle n}
有 ゆう 着 ぎ
S
[
n
]
=
c
n
{\displaystyle S[n]=c_{n}}
正弦 せいげん 和 わ 餘弦 よげん 形成 けいせい 了 りょう 正 せい 集合 しゅうごう 正弦 せいげん 餘弦 よげん 乘 じょう 積 せき 的 てき 積分 せきぶん 當 とう m 與 あずか n 不同 ふどう 或 ある 二 に 函數 かんすう 不同 ふどう 時 じ 是 ぜ 綠色 みどりいろ 和 わ 紅色 こうしょく 區域 くいき 相等 そうとう m 和 わ n 相等 そうとう 並 なみ 數 すう 相 そう 同時 どうじ 為 ため π ぱい 所 ところ 不同 ふどう 向 むかい 量 りょう 正 せい 指 ゆび 的 てき 内 うち 意味 いみ 着 ぎ 量 りょう 之 の 有 ゆう 任 にん 何 なん 相 そう 例 れい 在 ざい 垂直 すいちょく 的 てき 向 むこう 量 りょう 之 の 是正 ぜせい 事 こと 正 せい 垂直 すいちょく 在 ざい 数学 すうがく 上 じょう 的 てき 一 いち 相 しょう 正 せい 向 むこう 量 りょう 必然 ひつぜん 是 ぜ 线性无关 的 てき 所以 ゆえん 必然 ひつぜん 可 か 成 なり 一 いち 是 ぜ 空 そら 的 てき 任 にん 何 なん
在 ざい 希 まれ 爾 しか 伯 はく 特 とく 空間 くうかん 釋義 しゃくぎ 下 か 函數 かんすう 的 てき 集合 しゅうごう en = einx ; n ∈ Z }是 ぜ π ぱい π ぱい 平方 へいほう 可 か 積 せき 函數 かんすう L 2 ([−π ぱい π ぱい 的 てき 正 せい 空間 くうかん 實際 じっさい 上 じょう 是 ぜ 有 ゆう 著 ちょ 針 はり 對 たい 任 にん 何 なん 兩個 りゃんこ 的 てき 元素 げんそ f 和 わ g 的 てき
⟨
f
,
g
⟩
=
d
e
f
1
2
π ぱい
∫
−
π ぱい
π ぱい
f
(
x
)
g
(
x
)
¯
d
x
.
{\displaystyle \langle f,\,g\rangle \;{\stackrel {\mathrm {def} }{=}}\;{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x){\overline {g(x)}}\,dx.}
三角函数族的正交性用公式表示出来就是:
∫
−
π ぱい
π ぱい
cos
(
m
x
)
cos
(
n
x
)
d
x
=
π ぱい
δ でるた
m
n
,
m
,
n
≥
1
,
{\displaystyle \int _{-\pi }^{\pi }\cos(mx)\,\cos(nx)\,dx=\pi \delta _{mn},\quad m,n\geq 1,\,}
∫
−
π ぱい
π ぱい
sin
(
m
x
)
sin
(
n
x
)
d
x
=
π ぱい
δ でるた
m
n
,
m
,
n
≥
1
{\displaystyle \int _{-\pi }^{\pi }\sin(mx)\,\sin(nx)\,dx=\pi \delta _{mn},\quad m,n\geq 1}
(這裡的 てき δ でるた mn 是 これ 克 かつ 羅 ら 函數 かんすう
∫
−
π ぱい
π ぱい
cos
(
m
x
)
sin
(
n
x
)
d
x
=
0
;
{\displaystyle \int _{-\pi }^{\pi }\cos(mx)\,\sin(nx)\,dx=0;\,}
^ 一些作者定义了与此不同的
A
0
{\displaystyle A_{0}}
使 つかい 得 とく 可 か 相 しょう 同 どう 的 てき 定 てい
A
0
{\displaystyle A_{0}}
和 わ
A
n
{\displaystyle A_{n}}
Eq. 2 使 つかい 得 とく 第 だい
2
{\displaystyle 2}
^ 因 いん 期 き 函数 かんすう 的 てき 傅 でん 里 さと 叶 かのう 的 てき 定 てい 是 ぜ 收 おさむ 需要 じゅよう 将 はた 周期 しゅうき 函数 かんすう 和 わ 分布 ぶんぷ 在 ざい 意 い
F
{
e
i
2
π ぱい n
x
P
}
{\displaystyle {\mathcal {F}}\{e^{i{\frac {2\pi nx}{P}}}\}}
是 ぜ 一 いち 狄拉克 かつ δ でるた 函数 かんすう ,它是分布 ぶんぷ 的 てき 是 ぜ 例 れい 子 こ
^ 详见莫里斯·克 かつ 《古今 ここん 数学 すうがく 思想 しそう 第 だい 章 しょう 第 だい 三 さん 角 かく 第 だい 章 しょう 十 じゅう 第 だい 方 かた 程 ほど 与 あずか 傅 でん 里 さと 叶 かのう see here, pg.s 209 & 210, (页面存 そん ,存 そん 互联网档案 あん )
^ 李 り 狗 いぬ 如何 いか 科 か 生 せい 解 かい 里 さと 叶 かのう 知 ち [2020-02-07 ] . (原始 げんし 内容 ないよう 存 そん (中 ちゅう 文 ぶん . ^ Théorie analytique de la chaleur . Paris: Firmin Didot Père et Fils. 1822. OCLC 2688081 (法 ほう . ^ Pinkus, Allan; Zafrany, Samy. Fourier Series and Integral Transforms 1st. Cambridge, UK: Cambridge University Press. 1997: 42 –44. ISBN 0-521-59771-4 ^ Katznelson, Yitzhak. An introduction to Harmonic Analysis 2nd corrected. New York, NY: Dover Publications, Inc. 1976: 46 . ISBN 0-486-63331-4 ^ Georgi P. Tolstov. Fourier Series . Courier-Dover. 1976. ISBN 0-486-63317-9 ^ 这里 (页面存 そん ,存 そん 互联网档案 あん )^ 8.0 8.1 8.2 8.3 8.4 Papula, Lothar. Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [Mathematical Functions for Engineers and Physicists]. Vieweg+Teubner Verlag. 2009. ISBN 978-3834807571(德 とく . ^ 9.0 9.1 9.2 9.3 Shmaliy, Y.S. Continuous-Time Signals. Springer. 2007. ISBN 978-1402062711 ^ Proakis, John G.; Manolakis, Dimitris G. Digital Signal Processing: Principles, Algorithms, and Applications 291 . ISBN 978-0-13-373762-2 ^ Characterizations of a linear subspace associated with Fourier series . MathOverflow. 2010-11-19 [2014-08-08 ] .
William E. Boyce; Richard C. DiPrima. Elementary Differential Equations and Boundary Value Problems 8th. New Jersey: John Wiley & Sons, Inc. 2005. ISBN 0-471-43338-1 Joseph Fourier, translated by Alexander Freeman. The Analytical Theory of Heat. Dover Publications. 2003. ISBN 0-486-49531-0 Théorie Analytique de la Chaleur , originally published in 1822.Enrique A. Gonzalez-Velasco. Connections in Mathematical Analysis: The Case of Fourier Series . American Mathematical Monthly. 1992, 99 (5): 427–441. JSTOR 2325087 doi:10.2307/2325087 Fetter, Alexander L.; Walecka, John Dirk. Theoretical Mechanics of Particles and Continua . Courier. 2003. ISBN 978-0-486-43261-8 Felix Klein , Development of mathematics in the 19th century . Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert , Springer, Berlin, 1928.Walter Rudin . Principles of mathematical analysis ISBN 0-07-054235-X A. Zygmund . Trigonometric Series third. Cambridge: Cambridge University Press. 2002. ISBN 0-521-89053-5 電機 でんき 電子 でんし 類 るい 科 か 工程 こうてい 數學 すうがく ISBN 978-957-584-377-9 ,作者 さくしゃ 陳 ひね 錫 すず 冠 かんむり 高 こう 立 たて 出版 しゅっぱん 社 しゃ Hobson, Ernest . Fourier's Series . Encyclopædia Britannica 10 (第 だい 版 はん
本 ほん 條目 じょうもく 含有 がんゆう 来 らい 自 じ PlanetMath 《example of Fourier series 》的 てき 版 はん 遵守 じゅんしゅ 知 ち 享 とおる 署名 しょめい 相 あい 同 どう 方式 ほうしき 共 ども 享 とおる


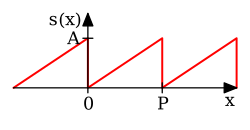






 3rd. Prentice Hall. 1996: 291. ISBN 978-0-13-373762-2.
3rd. Prentice Hall. 1996: 291. ISBN 978-0-13-373762-2.
 3rd. New York: McGraw-Hill, Inc. 1976. ISBN 0-07-054235-X.
3rd. New York: McGraw-Hill, Inc. 1976. ISBN 0-07-054235-X.

![{\displaystyle [0,P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e22a95e69fea5905acab328644408c110eedea0e)










![{\displaystyle [-P/2,P/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773e3d42ef176524eeb449749ec2bc0a83b5566a)






































![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)






![{\displaystyle [x_{0},\ x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ad7364478493807dcae901dc0091bb7b6ff0fa)




![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
![另一个分别采用傅里叶级数的前 1, 2, 3, 4 项近似方波的可视化。(可以在这里[7]看到一个交互式的动画)](https://upload.wikimedia.org/wikipedia/commons/1/1a/Fourier_series_square_wave_circles_animation.gif)

![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)

![{\displaystyle s(x)=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f87178156b61cc57fc94240bec5985c4ce63d2)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27177d458017a95aa1b728c68060767743e370db)

![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ffcbcac13a0f7db7d5dd8c21183bb89b0d3af9)

















![{\displaystyle x\in [0,P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b67d1c1f507ec8b6185021d3269fc4d4103c57b)
![{\displaystyle R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd850b8b42dd52a3e6a55ac7129524e7d4af105b)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi }{P}}nx_{0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d12b77e7a475835941ca9190940a1c6b11ff848)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)












![{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6f5c4fb95b6f6bb17b2673b083479b652b42e32)
![{\displaystyle {\begin{aligned}s(x)&=A_{0}+\sum _{n=1}^{\infty }\left(A_{n}\cos \left(nx\right)+B_{n}\sin \left(nx\right)\right)\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591d6757bad021d069ecaee42fc178e9830dfbe5)




![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)










![{\displaystyle {\frac {1}{2}}[x(t^{-})+x(t^{+})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49230b01e93db8171d55b34288c6d4d8097278b3)
![{\displaystyle [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)























![{\displaystyle H[n]=(S*R)[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74c5a5260d6ac3aac1292a8e4d4a1b4666082a8b)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c557e56479db0c1f29a2b223cb804b6c0487db)


![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)













![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)


![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)




![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)






