数学上(特别是代数拓扑和抽象代数),同调 (homology,在希腊语中homos = 同)是一类将一个可换群或者模的序列和特定数学对象(例如拓扑空间或者群)联系起来的过程。背景知识请参看同调论。
对于一个特定的拓扑空间,同调群通常比同伦群要容易计算得多,因此通常来讲用同调来辅助空间分类要容易处理一些。
同调群的构造[编辑]
其过程如下:给定对象 ,首先定义链复形,它包含了
,首先定义链复形,它包含了 的信息。一个链复形是一个由群同态联系起来的可换群或者模
的信息。一个链复形是一个由群同态联系起来的可换群或者模 的序列,群同态
的序列,群同态 满足任何两个相连的同态的复合为0:
满足任何两个相连的同态的复合为0:  对于所有
对于所有 成立。这意味着第
成立。这意味着第 个映射的像包含在第
个映射的像包含在第 个映射的核中,我们定义
个映射的核中,我们定义 的
的 阶同调群为商群(商模)
阶同调群为商群(商模)

链复形称为正合的,如果( )阶映射的像总是等于
)阶映射的像总是等于 阶映射的核。因此
阶映射的核。因此 的同调群是衡量
的同调群是衡量 所关联的链复形离正合有“多远”的障碍。
所关联的链复形离正合有“多远”的障碍。
非正式的例子[编辑]
非正式地,拓扑空间X的同调是X的拓扑不变量的集合,用其同调群来表示

其中第 个同调群
个同调群 描绘了
描绘了 中的
中的 维圈 (cycle),实现为
维圈 (cycle),实现为 维圆盘边界 (boundary) 的障碍。0维同调群刻画了两个零维圈,也即点,实现成一维圆盘,也即线段的边界的障碍,因此
维圆盘边界 (boundary) 的障碍。0维同调群刻画了两个零维圈,也即点,实现成一维圆盘,也即线段的边界的障碍,因此 刻画了
刻画了 中的道路连通分支。[1]
中的道路连通分支。[1]
 圆,或称为1维球面
圆,或称为1维球面
一维球面  是一个圆。它有一个连通分支和一个一维圈,但没有更高维圈。其对应的同调群由下式给出
是一个圆。它有一个连通分支和一个一维圈,但没有更高维圈。其对应的同调群由下式给出

其中 表示整数加群,
表示整数加群, 表示平凡群。
表示平凡群。 表示
表示 的一阶同调群为由一个元素生成的有限生成阿贝尔群,其唯一的生成元表示圆中包含的一维圈。[2]
的一阶同调群为由一个元素生成的有限生成阿贝尔群,其唯一的生成元表示圆中包含的一维圈。[2]
 2维球面
2维球面 即球的球壳,不包括球的内部。
即球的球壳,不包括球的内部。
二维球面 有一个连通分支,零个一维圈,一个二维圈(即球面),无更高维的圈,其对应的同调群为[2]
有一个连通分支,零个一维圈,一个二维圈(即球面),无更高维的圈,其对应的同调群为[2]

一般地,对 维球面
维球面 ,其同调群为
,其同调群为

 实心圆盘,即2维球
实心圆盘,即2维球
二维实心球 有一个道路连通分支,但与圆不同的是,
有一个道路连通分支,但与圆不同的是, 没有一维或更高维的圈,其对应的同调群除了零阶同调群
没有一维或更高维的圈,其对应的同调群除了零阶同调群 以外,其余阶的同调群均为平凡群。
以外,其余阶的同调群均为平凡群。
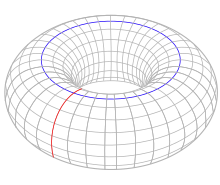 环面
环面
环面被定义为两个圆 的笛卡尔积。环面有一个道路连通分支,两个独立的一维圈(在图中以红圈和蓝圈分别标出),以及一个二维圈(环面的内部)。其对应的同调群为[3]
的笛卡尔积。环面有一个道路连通分支,两个独立的一维圈(在图中以红圈和蓝圈分别标出),以及一个二维圈(环面的内部)。其对应的同调群为[3]

两个独立的一维圈组成了一组有限生成阿贝尔群的独立生成元,表示为笛卡尔积群 .
.
例子[编辑]
引入同调的概念可以用单纯复形 的单纯同调:设
的单纯同调:设 为
为 中的
中的 维可定向单纯形生成的自由交换群或者模,映射
维可定向单纯形生成的自由交换群或者模,映射 映射称为边缘映射 (boundary map),它将
映射称为边缘映射 (boundary map),它将 维单纯形
维单纯形

映射为如下交错和
![{\displaystyle \sum _{i=0}^{n}(-1)^{i}\sigma |_{[e_{0},\ldots ,e_{i-1},e_{i+1},\ldots ,e_{n}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e11e774fc98437f3bac36b14dafdd97e62f45a7)
,其中![{\displaystyle \sigma |_{[e_{0},\cdots ,e_{i-1},e_{i+1},\cdots ,e_{n}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aefe194740189f56d06f32e315e33c98227b400c) 表示
表示 限制在
限制在 对应的面 (face)上。如果我们将模取在一个域上,则
对应的面 (face)上。如果我们将模取在一个域上,则 的
的 阶同调的维数就是
阶同调的维数就是 中
中 维圈的个数。
维圈的个数。
仿照单纯同调群,可以定义任何拓扑空间 的奇异同调群。我们定义
的奇异同调群。我们定义 的上同调的链复形中的空间为
的上同调的链复形中的空间为 为自由交换群(或者自由模),其生成元为所有从
为自由交换群(或者自由模),其生成元为所有从 为单纯形到
为单纯形到 的连续函数。同态
的连续函数。同态 从单纯形的边缘映射得到。
从单纯形的边缘映射得到。
同调代数中,同调用于定义导出函子,例如,Tor函子。这里,我们可以从某个可加协变函子 和某个模
和某个模 开始。
开始。 的链复形定义如下:首先找到一个自由模
的链复形定义如下:首先找到一个自由模 和一个满同态
和一个满同态 。然后找到一个自由模
。然后找到一个自由模 和一个满同态
和一个满同态 。以该方式继续,得到一个自由模
。以该方式继续,得到一个自由模 和同态
和同态 的序列。将函子
的序列。将函子 应用于这个序列,得到一个链复形;这个复形的同调
应用于这个序列,得到一个链复形;这个复形的同调 仅依赖于
仅依赖于 和
和 ,并且按定义就是
,并且按定义就是 作用于
作用于 的n阶导出函子。
的n阶导出函子。
同调函子[编辑]
链复形构成一个范畴:从链复形 到链复形
到链复形 的态射是一个同态的序列
的态射是一个同态的序列 ,满足
,满足 对于所有
对于所有 成立。
成立。 阶同调
阶同调  可以视为一个从链复形的范畴到可换群(或者模)的范畴的协变函子。
可以视为一个从链复形的范畴到可换群(或者模)的范畴的协变函子。
若链复形以协变的方式依赖于对象 (也就是任何态射
(也就是任何态射 诱导出一个从
诱导出一个从 的链复形到
的链复形到 的链复形的态射),则
的链复形的态射),则 是从
是从 所属的范畴到可换群(或模)的范畴的函子。
所属的范畴到可换群(或模)的范畴的函子。
同调和上同调的唯一区别是上同调中的链复形以逆变方式依赖于 ,因此其同调群(在这个情况下称为上同调群并记为
,因此其同调群(在这个情况下称为上同调群并记为 )构成从
)构成从 所属的范畴到可换群或者模的范畴的逆变函子。
所属的范畴到可换群或者模的范畴的逆变函子。
性质[编辑]
若 是链复形,满足出有限个
是链复形,满足出有限个 外所有项都是零,而非零的都是有限生成可换群(或者有限维向量空间),则可以定义欧拉示性数
外所有项都是零,而非零的都是有限生成可换群(或者有限维向量空间),则可以定义欧拉示性数

(可换群采用阶而向量空间的情况采用哈默尔维数)。事实上在同调水平上也可以计算欧拉示性数:

特别地,在代数拓扑中,欧拉示性数 是拓扑空间的重要不变量。
是拓扑空间的重要不变量。
此外,每个链复形的短正合序列

诱导一个同调群的长正合序列

这个长正合序列中的所有映射由链复形间的映射导出,除了映射 之外。后者称为连接同态,由蛇引理给出。
之外。后者称为连接同态,由蛇引理给出。
参看[编辑]
參考文獻[编辑]



































![{\displaystyle \sum _{i=0}^{n}(-1)^{i}\sigma |_{[e_{0},\ldots ,e_{i-1},e_{i+1},\ldots ,e_{n}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e11e774fc98437f3bac36b14dafdd97e62f45a7)
![{\displaystyle \sigma |_{[e_{0},\cdots ,e_{i-1},e_{i+1},\cdots ,e_{n}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aefe194740189f56d06f32e315e33c98227b400c)
























