Expectation
Expectation[expr,xdist]
x が
Expectation[expr,xdata]
x が data によって
Expectation[expr,{x1,x2,…}dist]
{x1,x2,…}が
Expectation[expr,{x1dist1,x2dist2,…}]
x1, x2, …が
Expectation[exprpred,…]
pred を
詳細 とオプション

- Expectationは
期待 値 としても知 られている. - xdist は x
 dist
dist dist または x \[Distributed]dist と
dist または x \[Distributed]dist と入力 できる. - exprpred は expr
 cond
cond pred または expr \[Conditioned]pred と
pred または expr \[Conditioned]pred と入力 できる. 連続 分布 dist では,expr の期待 値 は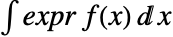 で
で与 えられる.ただし,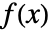 は dist の
は dist の確 率 密度 関数 であり,積分 は dist の領域 で行 われるものとする.離散 分布 dist では,expr の期待 値 は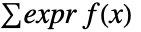 で
で与 えられる.ただし,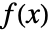 は dist の
は dist の確 率 密度 関数 であり,総和 は dist の領域 で行 われるものとする.- データ
集合 data では,expr の期待 値 はSum[expr,{x,data}]/Length[data]で与 えられる. 一 変量 データは値 のリスト{v1,v2,…}として,多 変量 データはベクトルのリスト{{v11,…,v1m},{v21,…,v2m},…}として与 えられる.- Expectation[expr,{x1dist1,x2dist2}]はExpectation[Expectation[expr,x2dist2],x1dist1]に
対応 するので,最後 の変数 が最初 に総和 を求 められたり積分 されたりする. - N[Expectation[…]]は
記号 的 に求 まらない期待 値 についてはNExpectationを呼 び出 す. » 使用 可能 なオプション-
Assumptions $Assumptions 母 数 についての仮定 »GenerateConditions False 母 数 についての条件 を生成 するかどうかMethod Automatic 使用 するメソッド »TargetUnits Automatic 出力 で表示 する単位 »
予備 知識
- Expectation[expr,x]は,
確 率 変数 x を含 む式 expr の,x が指示 された確 率 分布 に従 う(つまり, はNormalDistribution,BinomialDistribution,ChiSquareDistribution等 のような分布 である)か,あるいは指定 されたデータ集合 から取 られた(つまり, がデータ集合 を定義 する)場合 の期待 値 を与 える. はDistributedの短縮 表現 である.Expectationの出力 は,数値 あるいは入力 パラメータを含 む記号 式 であることがある. - Expectationは,
多 変量 分布 にも,EmpiricalDistribution,HistogramDistribution,KernelMixtureDistributionのようなノンパラメトリック多 変量 分布 にも,TransformedDistributionやProductDistribution等 の派生 分布 に使 うこともできる.Expectationは,ContinuousMarkovProcess,DiscreteMarkovProcess,WienerProcess,PoissonProcess等 で定義 されるものを含 むランダム過程 に使 うこともできる. - Expectationに
渡 された式 は,線形 および非線形 の式 や実数 および複素数 の変数 を持 つ関数 を含 むことがある.Expectationは,exprpred という形 を使 って条件 付 きの期待 値 を計算 することができる. はConditionedをの短縮 表現 である.Assumptions,GenerateConditions,Methodを含 む多 くのオプションをExpectationに渡 すことができる.Expectationの出力 は,記号 積分 や総和 を含 む厳密 メソッドで計算 される.これに対応 する数値 メソッドを含 む結果 はNExpectationで得 ることができる. 定義 上 ,分布 に従 って分布 している確 率 変数 x の期待 値 Expectation[x,x]は,第 1モーメントMoment[,1]に等 しく,したがって平均 Mean[]とも等 しい.加 えて,ExpectationとBoole構造 をペアにすると,Expectationから得 た結果 がProbability.からも得 られるようになる.例 えば,Expectation[Boole[1<x<3],xNormalDistribution[]]はProbability[1<x<3, xNormalDistribution[]]と等 しいのである.
例題
すべてスコープ (31)
基本 的 な用法 (9)
Assumptionsがない
Assumptionsがある
数量 の使用 (5)
QuantityDistributionを
QuantityMagnitudeで
Quantityデータで
QuantityArrayで
ノンパラメトリック分布 (4)
派生 分布 (9)
TransformedDistributionを
ProductDistributionを
オプション (6)
Assumptions (1)
Assumptionsがない
Assumptionsがある
Method (4)
Expectationの
ここでは,
Expectationの
TukeyLambdaDistribution
Quantileを
この
Activateを
TargetUnits (1)
アプリケーション (20)
分布 特性 (5)
ParameterMixtureDistributionを
保険 数理 (5)
ある![]() は
は ![]() では
では![]() に
に
ある![]() で
で![]() に
に![]() でモデル
でモデル
![]() については
については![]() の
の![]() は
は
![]() は
は![]() は
は![]() と
と ![]() の
の![]() と
と![]() については
については![]() で,その
で,その
![]() と
と ![]() の
の![]() の
の![]() と
と ![]() の
の
金融 (2)
![]() に
に![]() はGompertz–Makeham
はGompertz–Makeham
![]()
![]() はGompertz–Makeham
はGompertz–Makeham
![]() (
(![]() は,
は,![]() と
と ![]() の
の
![]() で
で![]() である
である
この![]() で
で
![]() でこの
でこの
コールオプションおよびプットオプションのリスク
これで,![]() である
である
![]() が5%,2%の
が5%,2%の![]() が0.087,
が0.087,
ランダムな実験 (2)
![]() からのサイズ10のランダムサンプルが
からのサイズ10のランダムサンプルが
![]() とExpectationの
とExpectationの
特性 と関係 (10)
NExpectationを
Expectationを
AsymptoticExpectationを
Asymptotic[Expectation[…]]を
Mean,Moment, Variance,その
MomentGeneratingFunctionを
リストで
考 えられる問題 (1)
デフォルトで,IntegrateのGenerateConditionsがFalseに
GenerateConditionsをTrueに
テキスト
Wolfram Research (2010), Expectation, Wolfram
CMS
Wolfram Language. 2010. "Expectation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/Expectation.html.
APA
Wolfram Language. (2010). Expectation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Expectation.html