Tetrahedron
Appearance
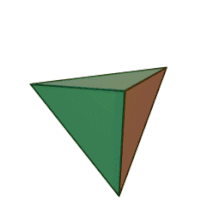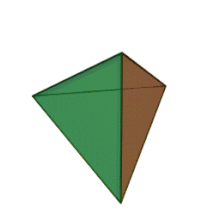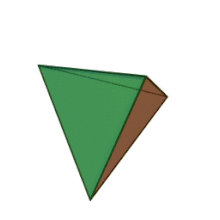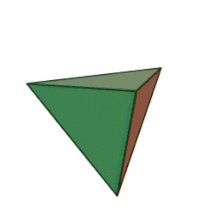
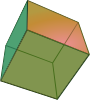
A tetrahedron or triangular pyramid is a polyhedron (a three-dimensional shape). It has four corners and six edges. All four of its faces are equilateral triangles. Every two edges meet on one of those corners forming a sixty-degree angle.
Formulas for a regular tetrahedron
[change | change source]A regular tetrahedron is a tetrahedron whose edges are the same length. If the length of an edge is a:
| Surface area[1] | |
| Face area | |
| Height[2] | and |
| Volume[1] | and |
Other properties
[change | change source]A regular tetrahedron's faces are all the same, and so are all its edges, as well as its corners. This makes it a regular polyhedron. It is also convex (its faces do not go through one another), which makes it a Platonic solid.
The dual of regular tetrahedron is another regular tetrahedron. This is called being self-dual.
References
[change | change source]- ↑ 1.0 1.1 Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
- ↑ Köller, Jürgen, "Tetrahedron", Mathematische Basteleien, 2001