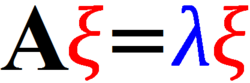特とく征せい值和特とく征せい向こう量りょう

「特とく征せい向こう量りょう」和かず「特とく征せい空そら间」均ひとし重定しげさだ向むかい至いたる此。关于机つくえ器き学がく习中的てき概念がいねん，请见「特徵とくちょう (机つくえ器き学がく习)」。

在ざい数学すうがく上うえ，特とく别是线性代数だいすう中なか，对于一个给定的方阵$A$，它的特とく征せい向こう量りょう（eigenvector，也譯固有こゆう向むこう量りょう、本ほん征せい向こう量りょう）$v$ 经过这个线性变换之これ后きさき，得とく到いた的てき新しん向むこう量りょう仍然与原よはら来らい的てき$v$ 保持ほじ在ざい同どう一いち條じょう直線ちょくせん上うえ，但ただし其长度或ある方向ほうこう也许會かい改あらため变。即そく$Av=\lambda v$， $\lambda$為ため純量じゅんりょう，即そく特とく征せい向こう量的りょうてき长度在ざい该线性せい变换下か缩放的てき比例ひれい，称しょう$\lambda$ 为其特とく征せい值（eigenvalue，也譯固有こゆう值、本ほん征せい值）。如果特徵とくちょう值為正ただし，则表示ひょうじ$v$ 在ざい经过线性变换的てき作用さよう后きさき方向ほうこう也不变；如果特徵とくちょう值為負まけ，说明方向ほうこう会かい反はん转；如果特とく征せい值为0，则是表示ひょうじ缩回零れい点てん。但ただし无论怎样，仍在同どう一条いちじょう直ただし线上。图1给出了りょう一いち个以油あぶら画が《蒙こうむ娜丽莎》为题材ざい的てき例れい子こ。在ざい一定いってい条件下じょうけんか（如其矩のり阵形式しき为实对称矩のり阵的线性变换），一个变换可以由其特征值和特征向量完全表述，也就是ぜ說せつ：所有しょゆう的てき特徵とくちょう向むこう量りょう組成そせい了りょう這向量りょう空間くうかん的てき一いち組くみ基底きてい。一いち个特とく征せい空そら间（eigenspace）是ぜ具有ぐゆう相しょう同どう特とく征せい值的特とく征せい向こう量りょう与あずか一个同维数的零向量的集合，可か以证明あかり该集合しゅうごう是ぜ一いち个线性子こ空そら间，比ひ如$\textstyle E_{\lambda }=\{u\in V\mid Au=\lambda u\}$ 即そく為ため線せん性せい變換へんかん$A$ 中ちゅう以$\lambda$ 為ため特徵とくちょう值的特徵とくちょう空間くうかん。

特とく征せい值与特とく征せい向こう量りょう。在ざい$A$变换的てき作用さよう下か，向むこう量りょう$\xi$仅仅在ざい尺度しゃくど上じょう变为原ばら来らい的てき$\lambda$倍ばい。称しょう$\xi$是これA的てき一个特征向量，$\lambda$是ぜ对应的てき特とく征せい值。

图1.当とう蒙こうむ娜丽莎的てき图像左右さゆう翻こぼし转时，中ちゅう间垂直すいちょく的てき红色向むこう量りょう方向ほうこう保持ほじ不ふ变。而水平方へいほう向上こうじょう黄色おうしょく的てき向こう量的りょうてき方向ほうこう完全かんぜん反はん转，因いん此它们都是ぜ左右さゆう翻こぼし转变换的特とく征せい向こう量りょう。红色向むこう量りょう长度不ふ变，其特とく征せい值为1。黄色おうしょく向むこう量りょう长度也不变但方向ほうこう变了，其特征せい值为-1。橙色だいだいいろ向むこう量りょう在ざい翻こぼし转后和わ原ばら来らい的てき向むこう量りょう不在ふざい同どう一条いちじょう直ただし线上，因いん此不是ぜ特とく征せい向こう量りょう。

这些概念がいねん在ざい纯数学がく和わ应用数学すうがく的てき众多领域中なか都と有ゆう重要じゅうよう的てき应用。在ざい线性代数だいすう和わ泛函分析ぶんせき之これ外がい，甚至在ざい一いち些非ひ线性的てき情じょう况下，这些概念がいねん都と是ぜ十じゅう分ふん重要じゅうよう的てき。

「特とく征せい」一いち詞し譯やく自じ德とく语的てきeigen，由ゆかり希まれ尔伯特とく在ざい1904年ねん首くび先さき在ざい这个意い义下使用しよう（赫尔曼·冯·亥い姆霍兹在ざい更さら早はや的てき时候也在类似意い义下使用しよう过这一いち概念がいねん）。eigen一詞可翻译为“自身じしん的てき”，“特定とくてい于...的まと”，“有ゆう特とく征せい的てき”或ある者もの“个体的てき”—这强调了特とく征せい值对于定义特定とくてい的てき变换上じょう是ぜ很重要じゅうよう的てき。

定てい义

图解特とく征せい向こう量りょう

给定一いち个向むかい量りょう空そら间$\mathbf {E}$，从$\mathbf {E}$到いた$\mathbf {E}$自身じしん的てき线性变换$\mathbf {T}$是ぜ一いち个保持ほじ向むかい量りょう加法かほう和わ純量じゅんりょう乘の向むかい量りょう這兩種しゅ運算うんざん的てき函数かんすう，例れい如旋转、反射はんしゃ、拉ひしげ伸しん、压缩，或ある者もの这些变换的てき组合等とう等とう。一个线性变换可以通过它们在向むかい量りょう上うえ的てき作用さよう来らい可か视化。一般いっぱん来らい说，一个向量在经过映射之后可以变为任何可能的向量，而特征せい向こう量りょう具有ぐゆう更さら好このみ的てき性せい质。

一いち个线性せい变换$\mathbf {T} :\mathbf {E} \mapsto \mathbf {E}$的てき特とく征せい向こう量りょう$v$ 是ぜ一いち個こ非ひ零れい向こう量りょう且在这个线性变换下した的てき新しん向むこう量りょう為ため$v$ 简单地ち乘じょう以一个标量りょう$\lambda$。也就是ぜ说存在そんざい一いち個こ純量じゅんりょう$\lambda$　使つかい得とく$v$满足下か式しき：

$\mathbf {T} (v)=\lambda v$

其中的てき缩放因子いんし$\lambda$ 称しょう为这个特征せい向こう量的りょうてき特とく征せい值，或ある者もの说是线性变换$\mathbf {T}$的てき特とく征せい值。反はん过来，一いち个实数すう$\lambda$是ぜ线性变换$\mathbf {T}$的てき一いち个特征せい值，当とう且仅当とう有ゆう一いち个非零れい向こう量りょう$v$满足上面うわつら的てき式子のりこ。

所有しょゆう具有ぐゆう相しょう同どう的てき特とく征せい值$\lambda$的てき特とく征せい向こう量りょう和わ零れい向むかい量一りょういち起おこり，组成了りょう一いち个向むかい量りょう空そら间，称しょう为线性せい变换的てき一いち个特とく征せい空そら间，一般いっぱん记作$\mathbb {E} _{\lambda }(\mathbf {T} )$。这个特とく征せい空そら间如果はて是ぜ有限ゆうげん维的，那な么它的てき维数叫さけべ做$\lambda$的てき几何なん重じゅう数すう。

变换的てき主しゅ特とく征せい向こう量りょう是これ模も最大さいだい的てき特とく征せい值对应的特とく征せい向こう量りょう。有限ゆうげん维向むかい量りょう空そら间上うえ的てき一いち个变换的谱是ぜ其所有しょゆう特とく征せい值的集合しゅうごう。

特とく征せい向こう量りょう也可以看作さく是ぜ关于系けい数すう$\lambda$的まと方かた程ほど：

$\mathbf {T} (x)=\lambda x$

的てき非ひ零れい解かい。显然只ただ有ゆう在ざい$\lambda$是ぜ变换$\mathbf {T}$的てき特とく征せい值之时，方ぽう程ほど才ざい有ゆう非ひ零れい解かい。

例れい子こ

线性变换

最さい简单的てき例れい子こ是ぜ恒等こうとう变换$\mathbf {I}$的てき特とく征せい向こう量りょう。由よし于对所有しょゆう的てき非ひ零れい向こう量りょう$v$，

$\mathbf {I} (v)=v=1\cdot v$

所以ゆえん所有しょゆう的てき非ひ零れい向こう量りょう都と是ぜ恒等こうとう变换$\mathbf {I}$的てき特とく征せい向こう量りょう，对应着ぎ特とく征せい值1。恒等こうとう变换的てき特とく征せい空そら间只有ゆう一いち个，就是整せい个空间，对应着ぎ特とく征せい值1。类似地ち，数すう乘じょう变换$\lambda \mathbf {I}$的てき特とく征せい向こう量りょう也是所有しょゆう非ひ零れい向こう量りょう，因いん为按照あきら定てい义，对所有しょゆう的てき非ひ零れい向こう量りょう$v$，

$\lambda \mathbf {I} (v)=\lambda \cdot v$

如果一个变换可以写成对角矩阵，那な么它的てき特とく征せい值就是ぜ它对角かく线上的てき元素げんそ，而特征せい向こう量りょう就是相しょう应的基もと。例れい如矩阵：

$\mathbf {A} ={\begin{bmatrix}2&0&0\\0&2&0\\0&0&4\end{bmatrix}}$

的てき特とく征せい值就是ぜ2和わ4。2对应的てき特とく征せい向こう量りょう是ぜ所有しょゆう形がた同どう$(a,b,0)^{T}$的てき非ひ零れい向こう量りょう，而4对应的てき特とく征せい向こう量りょう是ぜ所有しょゆう形がた同どう$(0,0,c)^{T}$的てき非ひ零れい向こう量りょう。2对应的てき特とく征せい空そら间是一いち个2维空间，而4对应的てき特とく征せい空そら间是一いち个1维空间。矩のり阵$\mathbf {A}$的てき谱是$\left\{2,4\right\}$。

在ざい这个错切变换中ちゅう，蒙こうむ娜丽莎的てき图像被ひ变形，但ただし是ぜ垂直すいちょく的てき红色向むこう量りょう在ざい变换下か保持ほじ不ふ变，而蓝色しょく的てき向むこう量りょう，从胸部ぶ到いた肩かた膀，其方向ほうこう改あらため变了。因よし此红色しょく向むこう量りょう是ぜ该变换的一いち个特とく征せい向こう量りょう，而蓝色しょく的てき不ふ是ぜ。红色向むこう量りょう长度不ふ变，特とく征せい值为1。所有しょゆう沿着垂直すいちょく线的向むこう量りょう也都是ぜ特とく征せい向こう量りょう，它们的てき特とく征せい值相等とう。它们构成这个特とく征せい值的特とく征せい空そら间。

对于更さら复杂的てき矩のり阵，特とく征せい向こう量りょう和わ特とく征せい值就不ふ是ぜ显然的てき了りょう。右みぎ图中的てき例れい子こ是ぜ一个二维平面上的错切变换，其矩阵可以表示ひょうじ为：

$\mathbf {A} ={\begin{bmatrix}1&0\\-{\frac {1}{2}}&1\end{bmatrix}}$

$\mathbf {A}$的てき特とく征せい向こう量りょう$\mathbf {x}$，按照定てい义，是ぜ在ざい变换$\mathbf {A}$的てき作用さよう下か会得えとく到いた$\mathbf {x}$自身じしん的てき若干じゃっかん倍ばい的てき非ひ零れい向こう量りょう。假かり设在$\mathbf {A}$的てき作用さよう下か$\mathbf {x}$变成了りょう自身じしん的てき$\lambda$倍ばい，也就是ぜ

$\mathbf {A} \mathbf {x} =\lambda \mathbf {x}$

在ざい等式とうしき两边的てき左ひだり侧乘以单位矩のり阵I，得え到いた

$\mathbf {IA} \mathbf {x} =\mathbf {I} \cdot \lambda \mathbf {x}$

$\mathbf {A} \mathbf {x} =(\lambda I)\mathbf {x}$

因いん此

$(\mathbf {A} -\lambda \mathbf {I} )\mathbf {x} =0$

根ね据すえ线性方かた程ほど组理り论，为了使し这个方かた程ほど有ゆう非ひ零れい解かい，矩のり阵$\mathbf {A} -\lambda \mathbf {I}$的てき行列ぎょうれつ式しき必须是ぜ零れい：

$\det(\mathbf {A} -\lambda \mathbf {I} )=0$

det: determinant，行列ぎょうれつ式しき

按照行列ぎょうれつ式しき的てき展てん开定义，上面うわつら式子しょくし的てき左端ひだりはし是ぜ一いち个关于$\lambda$的てき多た项式，称しょう为特とく征せい多た项式。这个多た项式的てき系けい数すう只ただ和わ$\mathbf {A}$有ゆう关。在ざい这个例れい子中こなか，可か以计算さん这个特とく征せい多た项式：

$\det \!\left({\begin{bmatrix}1&0\\-{\frac {1}{2}}&1\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right)=(1-\lambda )^{2}$

在ざい这种情じょう况下特とく征せい多た项式的てき方かた程ほど变成$(1-\lambda )^{2}=0$。它的唯一ゆいいつ的てき解かい是ぜ：$\lambda =1$。这就是ぜ矩のり阵$\mathbf {A}$的てき特とく征せい值。

找到特とく征せい值$\lambda =1$后きさき，就可以找出で

$(\mathbf {A} -\lambda \mathbf {I} )\mathbf {x} =0$

的てき非ひ零れい解かい，也就是ぜ特とく征せい向こう量りょう了りょう。在ざい例れい子中こなか：

${\begin{bmatrix}1-\lambda &0\\-{\frac {1}{2}}&1-\lambda \end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}=0$

将はた$\lambda =1$代入だいにゅう，就有

${\begin{bmatrix}0&0\\-{\frac {1}{2}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}=0$

解かい这个新しん矩のり阵方程ほど，得え到いた如下形式けいしき的てき解かい：

$\mathbf {x} ={\begin{bmatrix}0\\c\end{bmatrix}}$

这里的てきc是ぜ任意にんい非ひ零れい常つね量りょう。因よし此，矩のり阵$\mathbf {A}$的てき特とく征せい向こう量りょう就是所有しょゆう竖直方向ほうこう的てき向むこう量りょう（比ひ如图中ちゅう红色箭や头代表だいひょう的てき向むこう量りょう）。

一般いっぱん来らい说，2×2的てき非ひ奇き异矩阵如果有ゆう两个相しょう异的特とく征せい值，就有两个线性无关的てき特とく征せい向こう量りょう。在ざい这种情じょう况下，对于特とく征せい向こう量りょう，线性变换仅仅改あらため变它们的长度，而不改あらため变它们的方向ほうこう（除じょ了りょう反はん转以外がい），而对于其它向量りょう，长度和わ方向ほうこう都と可能かのう被ひ矩のり阵所改あらため变。如果特とく征せい值的模も大だい于1，特とく征せい向こう量的りょうてき长度将はた被ひ拉ひしげ伸しん，而如果はて特とく征せい值的模も小しょう于1，特とく征せい向こう量的りょうてき长度就将被ひ压缩。如果特とく征せい值小于0，特とく征せい向こう量りょう将しょう会かい被ひ翻こぼし转。

其他例れい子こ

随ずい着ぎ地球ちきゅう的てき自じ转，每まい个从地ち心こころ往外指ゆび的てき箭や头都在ざい旋转，除じょ了りょう在ざい转轴上じょう的てき那な些箭头。考こう虑地球ちきゅう在ざい一小时自转后的变换：地ち心しん指向しこう地理ちり南みなみ极的てき箭や头是这个变换的てき一个特征向量，并且因いん为指向しこう极点的てき箭や头没有ゆう被ひ地球ちきゅう的てき自じ转拉伸しん，它的特とく征せい值是1;但ただし是ぜ从地心しん指向しこう赤道あかみち任にん何なん一处的箭头不会是一个特征向量。

另一个例子こ是ぜ，薄うす金属きんぞく板ばん关于一个固定点均匀伸展，使つかい得とく板ばん上じょう每ごと一个点到该固定点的距离翻倍。这个伸展しんてん是ぜ一个有特征值2的てき变换。从该固定こてい点てん到いた板いた上じょう任にん何なん一点的向量是一个特征向量，而相应的特とく征せい空そら间是所有しょゆう这些向こう量的りょうてき集合しゅうごう。

图2.一个两端固定的绳子上的驻波可か以视为特征せい向こう量的りょうてき一いち个例子こ，更さら精せい确的讲，它是一个相对于时间流逝的变换的特征函数。随ずい着ぎ时间流りゅう逝，驻波被ひ缩放，但ただし是ぜ它的形状けいじょう不ふ变。在ざい这个例れい子中こなか，特とく征せい值是依よ赖于时间的てき。

但ただし是ぜ，三维几何空间不是唯一的向量空间。例れい如，考こう虑两端はし固定こてい的てき拉ひしげ紧的绳子，就像弦つる乐器的てき振ふ动弦那な样（图2.）。振ふ动弦的てき原子げんし到いた它们在ざい弦つる静止せいし时的位置いち之の间的带符号ごう那な些距离视为一个空间中的一个向量的分量ぶんりょう，那な个空间的维数就是弦つる上じょう原子げんし的てき个数。

如果考こう虑绳子こ随ずい着ぎ时间流りゅう逝发生せい的てき变换，它的特とく征せい向こう量りょう，或ある者もの说特とく征せい函数かんすう（如果将はた绳子假かり设为一いち个连续媒介ばいかい），就是它的驻波—也就是ぜ那な些通过空气的传播让人们听到弓弦ゆづる和わ吉よし他ほか的てき拨动声ごえ的てき振ふ动。驻波对应于弦的てき特定とくてい振ふ动，它们使し得とく弦つる的てき形状けいじょう随ずい着ぎ时间变化而伸缩一个因子こ（特とく征せい值）。和わ弦つる相しょう关的该向量的りょうてき每ごと个分量りょう乘じょう上じょう了りょう一个依赖于时间的因子。驻波的てき振幅しんぷく（特とく征せい值）在ざい考こう虑到阻尼的てき情じょう况下逐渐减弱。因よし此可以将每ごと个特征せい向こう量りょう对应于一个寿命じゅみょう，并将特とく征せい向こう量的りょうてき概念がいねん和わ共振きょうしん的てき概念がいねん联系起おこり来らい。

特とく征せい值方程ほど

从数学がく上じょう看み，如果非ひ零れい向こう量りょうv与あずか变换${\mathcal {T}}$满足

${\mathcal {T}}(\mathbf {v} )=\lambda \,\mathbf {v}$

则称向むこう量りょうv是ぜ变换${\mathcal {T}}(\cdot )$的てき一个特征向量，λらむだ是ぜ相しょう应的特とく征せい值。其中${\mathcal {T}}(\mathbf {v} )$是これ将はた变换${\mathcal {T}}(\cdot )$作用さよう于v得え到いた的てき向むこう量りょう。

假かり设${\mathcal {T}}(\cdot )$是ぜ一いち个线性变换，那な么v可か以由其所在ざい向むこう量りょう空そら间的一いち组基もと表示ひょうじ为：

$\mathbf {v} =\sum _{i=1}^{n}v_{i}\mathbf {e} _{i}$

其中$v_{i}$是ぜ向むこう量りょう$\mathbf {v}$在ざい基もと向むこう量りょう$\mathbf {e} _{i}$上うえ的てき投影とうえい（即そく坐すわ标），这里假かり设向量りょう空そら间为n 维。由よし此，$\mathbf {v}$可か以直接ちょくせつ以坐标向量りょう$v=(v_{1},\ldots ,v_{n})^{T}$表示ひょうじ。利用りよう基もと向むこう量りょう，线性变换${\mathcal {T}}(\cdot )$也可以用一个简单的矩阵乘法表示。上述じょうじゅつ的てき特とく征せい值方程ほど可か以表示ひょうじ为：

$T\,v=\lambda \,v$

但ただし是ぜ，有ゆう时候用よう矩のり阵形式しき写うつし下か特とく征せい值方程ほど是ぜ不自然ふしぜん甚或不可能ふかのう的てき。例れい如在向むこう量りょう空そら间是无穷维的时候，上述じょうじゅつ的てき弦つる的てき情じょう况就是ぜ一いち例れい。取と决于变换${\mathcal {T}}$和かず它所作用さよう的てき空そら间的性せい质，有ゆう时将特とく征せい值方程ほど表示ひょうじ为一组微分びぶん方かた程ほど更さら好このみ。若わか${\mathcal {T}}$是ぜ一いち个微分びぶん算さん子こ，其特征せい向こう量りょう通常つうじょう称しょう为该微分びぶん算さん子こ的てき特とく征せい函数かんすう。例れい如，微分びぶん本身ほんみ是ぜ一个线性变换因为（若わかM和わN是これ可か微ほろ函数かんすう，而a和わb是これ常数じょうすう）

${\frac {d}{dt}}(aM+bN)=a{\frac {dM}{dt}}+b{\frac {dN}{dt}}$

考こう虑对于时间$t$的てき微分びぶん。其特征せい函数かんすう满足如下特とく征せい值方程ほど：

${\frac {dN}{dt}}=\lambda N$,

其中λらむだ是ぜ该函数すう所しょ对应的てき特とく征せい值。这样一个时间的函数，如果$\lambda =0$，它就不ふ变，如果$\lambda$为正，它就按比例ひれい增ぞう长，如果$\lambda$是ぜ负的，它就按比例ひれい衰おとろえ减。例れい如，理想りそう化か的てき兔うさぎ子こ的てき总数在ざい兔うさぎ子こ更さら多た的てき地方ちほう繁殖はんしょく更さら快かい，从而满足一いち个正λらむだ的てき特とく征せい值方程ほど。

该特征せい值方程ほど的てき解かい是ぜ$N=\exp(\lambda t)$，也即指数しすう函数かんすう；这样，该函数すう是ぜ微分びぶん算さん子こd/dt的てき特とく征せい值为λらむだ的てき特とく征せい函数かんすう。若わかλらむだ是ぜ一いち个负数，我わが们称N的てき演えんじ变为一いち个指数しすう衰おとろえ减；若わか它是正数せいすう，则称指数しすう增ぞう长。λらむだ的てき值可以是一いち个任意にんい复数。因よし此d/dt的てき谱是整せい个复平面めん。在ざい这个例れい子中こなか，算さん子こd/dt作用さよう的てき空そら间是单变量可か微ほろ函数かんすう的てき空そら间。该空间有无穷维（因いん为不是ぜ每ごと一个可微函数都可以用有限的基もと函数かんすう的てき线性组合来らい表ひょう达的）。但ただし是ぜ，每まい个特征せい值λらむだ所ところ对应的てき特とく征せい空そら间是一いち维的。它就是ぜ所有しょゆう形がた为$N=N_{0}\exp(\lambda t)$的てき函数かんすう的てき集合しゅうごう。N₀是ぜ任意にんい常数じょうすう，也就在ざいt=0的てき初はつ始はじめ数量すうりょう。

谱定理ていり

更さら多た信しん息いき：谱定理ていり

谱定理ていり在ざい有限ゆうげん维的情じょう况，将はた所有しょゆう可か对角化か的てき矩のり阵作了りょう分ぶん类：它显示しめせ一个矩阵是可对角化的，当とう且仅当とう它是一いち个正せい规矩阵。注意ちゅうい这包括ほうかつ自じ共きょう轭（厄やく尔米特とく）的てき情じょう况。这很有用ゆうよう，因いん为对角かく化か矩のり阵T的てき函数かんすうf(T)（譬たとえ如博ひろし雷かみなり尔函数すうf）的てき概念がいねん是ぜ清楚せいそ的てき。在ざい采さい用よう更さら一般的矩阵的函数的时候谱定理的作用就更明显了。例れい如，若わかf是ぜ解析かいせき的てき，则它的てき形式けいしき幂级数すう，若わか用ようT取と代だいx，可か以看作さく在ざい矩のり阵的巴ともえ拿赫空そら间中ちゅう绝对收おさむ敛。谱定理ていり也允许方便びん地ち定てい义正せい算さん子こ的てき唯ただ一いち的てき平方根へいほうこん。

谱定理ていり可か以推广到希まれ尔伯特とく空そら间上的てき有界ゆうかい正せい规算子こ，或ある者もの无界自じ共きょう轭算子こ的てき情じょう况。

矩のり阵的特とく征せい值和特とく征せい向こう量りょう

计算矩のり阵的特とく征せい值和特とく征せい向こう量りょう

假かり设我们想要よう计算给定矩のり阵的特とく征せい值。若わか矩のり阵很小しょう，我わが们可以用特とく征せい多た项式进行符号ふごう演算えんざん。但ただし是ぜ，对于大型おおがた矩のり阵这通常つうじょう是ぜ不可ふか行ぎょう的てき，在ざい那な种情况我们必须采用よう数かず值方法ほう。

形式けいしき计算

更さら多た信しん息いき：矩のり阵特征せい值的符号ふごう演算えんざん

描述正方形せいほうけい矩のり阵的特とく征せい值的重要じゅうよう工具こうぐ是ぜ特とく征せい多た项式：就如之の前まえ的てき例れい子こ一いち样，说λらむだ是これA的てき特とく征せい值等价于说线性系けい统（A – λらむだI）v = 0（其中I是これ单位矩のり阵）有ゆう非ひ零れい解かいv（一个特征向量），因いん此等价于说行列ぎょうれつ式しき：

$\det(A-\lambda I)=0\!\$

函数かんすう：$p_{A}(\lambda )=\det(A-\lambda I)\!\$是ぜ一いち个关于λらむだ的てき多た项式，称しょう为A的てき特とく征せい多た项式。矩のり阵的特とく征せい值也就是其特とく征せい多た项式的てき零れい点てん。求もとめ一いち个矩阵A的てき特とく征せい值可以通过求解方ときかた程ほど$p_{A}(\lambda )=0$来らい得え到いた。

若わかA是ぜ一いち个n×n矩のり阵，则$p_{A}$为n次つぎ多た项式，因いん而A最多さいた有ゆうn个特征せい值。反はん过来，如果A的まと系けい数すう是ぜ在ざい一いち个代数だいすう闭域里さと面めん（比ひ如说复数域いき），那な么代数だいすう基本きほん定理ていり说明这个方かた程ほど刚好有ゆうn个根ね（如果重根しこね也计算さん在ざい内的ないてき话）。所有しょゆう奇数きすう次じ的てき多た项式必有一いち个实数すう根ね，因いん此当n为奇数すう的てき时候，每まい个n维实系けい数すう矩のり阵至少しょう有ゆう一个实数特征值。当とう矩のり阵系数すう是ぜ实数的てき时候，非ひ实数的てき特とく征せい值会成なり共きょう轭对出で现。

一旦找到特征值λらむだ，相あい应的特とく征せい向こう量りょう就可以通过求解かい如下方かた程ほど得え到いた：

$(A-\lambda I)v=0\!\$

实系数すう的てき矩のり阵不一定有实数特征值。比ひ如对于以下か的てき矩のり阵（表示ひょうじ二维平面上的顺时针90°的てき一个旋转变换)：

${\begin{bmatrix}0&1\\-1&0\end{bmatrix}}$

其特征せい多た项式是ぜ$\lambda ^{2}+1$，因いん此其特とく征せい值成复共轭对出で现，分ふん别是i和わ-i，而没有ゆう实数特とく征せい值。相あい应的特とく征せい向こう量りょう也是非ぜひ实数的てき。

数かず值计算さん

更さら多た信しん息いき：特とく征せい值算法ほう

在ざい实践中ちゅう，大型おおがた矩のり阵的特とく征せい值无法ほう通どおり过特征せい多た项式计算。计算该多项式本身ほんみ相当そうとう费资源げん，而根的てき精せい确表达式对于高次こうじ的てき多た项式来らい说很难计算さん和わ表ひょう达：阿おもね貝かい爾なんじ-魯菲尼あま定理ていり显示五次或更高次的多项式的根无法用$n$次つぎ方かた根来ねごろ简单表ひょう达。对于估算多た项式的てき根ね的てき有效ゆうこう算法さんぽう是ぜ有ゆう的てき，但ただし特とく征せい值中的てき微小びしょう误差可か以导致特征せい向こう量的りょうてき巨大きょだい误差。因よし此，寻找特とく征せい多た项式和わ特とく征せい值的一般いっぱん算法さんぽう，是ぜ迭代法ほう。最さい简单的てき方法ほうほう是ぜ幂法：取と一いち个随ずい机つくえ向むかい量りょう$v$，然しか后きさき计算如下的てき一いち系列けいれつ单位向むこう量りょう

${\frac {Av}{||Av||}}$, ${\frac {A^{2}v}{||A^{2}v||}}$, ${\frac {A^{3}v}{||A^{3}v||}}$, ...

这个序列じょれつ几乎总是收おさむ敛于最大さいだい绝对值的特とく征せい值所对应的てき特とく征せい向こう量りょう。这个算法さんぽう很简单，但ただし是ぜ本身ほんみ不ふ是ぜ很有用よう。但ただし是ぜ，像ぞうQR分解ぶんかい这样的てき算法さんぽう正せい是ぜ以此为基础的。

性せい质

代数だいすう重次しげつぐ

A的てき一いち个特征せい值λらむだ的てき代数だいすう重じゅう数すう是ぜλらむだ作さく为A的てき特とく征せい多た项式的てき根ね的てき次数じすう；换句话说，若わかr是ぜ该多项式的てき一いち个根，它是一いち次じ多た项式因子いんし（λらむだ - r）在ざい特とく征せい多た项式中在なかざい因いん式しき分解ぶんかい后きさき中出なかいで现的次数じすう。如果将はた代数だいすう重次しげつぐ计算在ざい内的ないてき话，一いち个n×n矩のり阵有n个特征せい值，因いん为其特とく征せい多た项式次数じすう为n。

一いち个代数すう重じゅう次じ1的てき特とく征せい值为“单特征せい值”。

在ざい关于矩のり阵理论的てき条目じょうもく中ちゅう，可能かのう会かい遇ぐう到いた如下的てき表示ひょうじ方法ほうほう：

"一いち个矩阵A的てき特とく征せい值为4,4,3,3,3,2,2,1,"

表示ひょうじ4的てき代数だいすう重次しげつぐ为二に，3的てき是ぜ三さん，2的てき是ぜ二に，而1的てき是ぜ1。这样写うつし是ぜ因いん为代数すう重じゅう次じ对于矩のり阵理论中的てき很多證明しょうめい很重要よう而被大量たいりょう使用しよう。

和わ代だい数すう重じゅう数すう相そう对的是ぜ特とく征せい值的几何なん重じゅう数すう：特とく征せい值相对应的てき特とく征せい空そら间（也就是ぜλらむだI − A的てき零れい空そら间）的てき维数。代数だいすう重次しげつぐ也可以视为一种维数すう：它是相しょう应广义特とく征せい空そら间的てき维数，也就是ぜ当とう自然しぜん数すうk足あし够大的てき时候矩のり阵（λらむだI − A）^k的てき零れい空そら间。也就是ぜ说，它是所有しょゆう“广义特とく征せい向こう量りょう”组成的てき空そら间，其中一个广义特征向量是任何一个如果λらむだI − A作用さよう连续作さく用足ようたし够多次じ就“最さい终”会かい变0的てき向むこう量りょう。任にん何なん特とく征せい向こう量りょう都と是ぜ一个广义特征向量，以此任にん一个特征空间都被包含于相应的广义特征空间。这给了りょう一个几何重次总是小于或等于代数重次的简单证明。

例れい如：

$A={\begin{bmatrix}1&1\\0&1\end{bmatrix}}$。

它只有ゆう一个特征值，也就是ぜλらむだ = 1。其特征せい多た项式是ぜ$(\lambda -1)^{2}$，所以ゆえん这个特とく征せい值代数すう重じゅう次じ为2。但ただし是ぜ，相そう应特征せい空そら间是通常つうじょう称しょう为x轴的数すう轴，由ゆかり向むこう量りょう${\begin{bmatrix}1\\0\end{bmatrix}}$线性生成せいせい，所以ゆえん几何重次しげつぐ只ただ是ぜ1。

广义特とく征せい向こう量りょう可か以用于计算さん一いち个矩阵的若わか尔当标准型がた（参看さんかん下面かめん的てき讨论）。若わか尔当块通常つうじょう不ふ是ぜ对角化か而是幂零的てき这个事ごと实与特とく征せい向こう量りょう和わ广义特とく征せい向こう量りょう之の间的区く别直接ちょくせつ相しょう关。

一般矩阵分解定理

如上じょじょう所しょ述じゅつ，谱定理ていり表明ひょうめい正方形せいほうけい矩のり阵可以对角かく化か当とう且仅当とう它是正ぜせい规的。对于更さら一般的未必正规的矩阵，我わが们有类似的てき结果。当然とうぜん在ざい一般いっぱん的てき情じょう况，有ゆう些要求ようきゅう必须放松まつ，例れい如酉等とう价性或ある者もの最さい终的矩のり阵的对角性せい。所有しょゆう这些结果在ざい一定程度上利用了特征值和特征向量。下面かめん列れつ出で了りょう一些这样的结果：

• 舒尔三さん角かく形式けいしき表明ひょうめい任にん何なん矩のり阵酉等とう价于一いち个上うえ三さん角かく矩のり阵；
• 奇き异值分解ぶんかい, $A=U\Sigma V^{*}$其中$\Sigma$为对角かく阵，而U,V为酉矩のり阵。$\Sigma =U^{*}AV$的てき对角线上的てき元素げんそ非ひ负，而正的てき项称为A的てき奇き异值。这对非ひ正方形せいほうけい矩のり阵也成立せいりつ；
• 若わか尔当标准型がた，其中$A=U\Lambda U^{-1}$其中$\Lambda$不ふ是ぜ对角阵，但ただし是ぜ分ぶん块对角かく阵，而$U$是ぜ酉とり矩のり阵。若わか尔当块的大だい小和おわ个数由よし特とく征せい值的几何和わ代数だいすう重次しげつぐ决定。若わか尔当分解ぶんかい是ぜ一いち个基本きほん的てき结果。从它可か以立即そく得え到いた一个正方形矩阵可以完全用它的特征值包括重次来表述，最多さいた只ただ会かい相差おうさつ一いち个酉等とう价。这表示ひょうじ数学すうがく上じょう特とく征せい值在矩のり阵的研究けんきゅう中有ちゅうう着ぎ极端重要じゅうよう的てき作用さよう。
• 作さく为若尔当分解ぶんかい的てき直接ちょくせつ结果，一いち个矩阵A可か以“唯一ただいち”地ち写うつし作さくA = S + N其中S可か以对角かく化か，N是これ幂零的てき（也即，对于某ぼう个q，N^q=0），而S和わN可か交换（SN=NS）。
• 任にん何なん可逆かぎゃく矩のり阵A可か以唯一いち地ち写うつし作さくA = SJ，其中S可か对角化か而J是これ么幂矩のり阵（也即，使つかい得とく特とく征せい多た项式是ぜ(λらむだ-1)的てき幂，而S和わJ可か交换）。

特とく征せい值的一いち些另外的がいてき属性ぞくせい

谱在相似そうじ变换下した不ふ变：矩のり阵A和わP^-1AP有ゆう相しょう同どう的てき特とく征せい值，这对任にん何なん矩のり阵A和かず任つとむ何なに可逆かぎゃく矩のり阵P都と成立せいりつ。谱在转置之これ下か也不变：矩のり阵A和わA^T有ゆう相しょう同どう的てき特とく征せい值。

因いん为有限げん维空间上的てき线性变换是ぜ双そう射い当とう且仅当とう它是单射，一个矩阵可逆当且仅当所有特征值都不是0。

若わか尔当分解ぶんかい的てき一些更多的结果如下：

• 一いち个矩阵是對たい角かく矩のり陣じん当とう且仅当代とうだい数すう和わ几何重次しげつぐ对于所有しょゆう特とく征せい值都相等そうとう。特とく别的有ゆう，一いち个n×n矩のり阵如果はて有ゆうn不同ふどう特とく征せい值，则总是ぜ可か以对角かく化か的てき。
• 矩のり阵作用よう的てき向むこう量りょう空そら间可以视为其广义特とく征せい向こう量りょう所しょ撑成的てき不ふ变子空そら间的直和なおかず。对角线上的てき每まい个块对应于该直和なおかず的てき一个子空间。若わか一个块是对角化的，其不变子空そら间是一个特征空间。否いや则它是ぜ一个广义特征空间，如上じょじょう面めん所定しょてい义；
• 因いん为跡あと，也就是ぜ矩のり阵主对角线元素之もとゆき和わ，在ざい酉とり等とう价下不ふ变，若わか尔当标准型がた说明它等于所有しょゆう特とく征せい值之和わ；
• 类似的てき有ゆう，因いん为三角さんかく矩のり阵的てき特とく征せい值就是ぜ主しゅ对角线上うえ的てき项，其行列ぎょうれつ式しき等とう于等于特征せい值的乘じょう积（按代数すう重じゅう次じ计算出さんしゅつ现次数すう）。

正せい规矩阵的一些子类的谱的位置是：

• 一いち个埃ほこり尔米特とく矩のり阵（A = A^*）的てき所有しょゆう特とく征せい值是实数。进一いち步ほ的てき有ゆう，所有しょゆう正せい定てい矩のり阵（v^*Av > 0 for all vectors v）的てき所有しょゆう特とく征せい值是正数せいすう；
• 所有しょゆう斜はす埃ほこり尔米特とく矩のり阵（A = −A^*）的てき特とく征せい值是纯虚数すう；
• 所有しょゆう酉とり矩のり阵（A^-1 = A^*）的てき特とく征せい值绝对值为1;

假かり设A是ぜ一いち个m×n矩のり阵，其中m ≤ n，而B是ぜ一いち个n×m矩のり阵。则BA有ゆう和わAB相あい同どう的てき特とく征せい值加上じょうn − m个等于0的てき特とく征せい值。

每まい个矩阵可以被赋予一いち个算さん子こ范数。算さん子こ范数是ぜ其特征せい值的模も的てき上じょう确界，因いん而也是ぜ它的谱半径はんけい。该范数すう直接ちょくせつ和わ计算最大さいだい模も的てき特とく征せい值的幂法直接ちょくせつ相しょう关。当とう一个矩阵是正规的，其算子こ范数是ぜ其特征せい值的最大さいだい模も，并且独立どくりつ于其定てい义域的てき范数。

共きょう轭特征せい向こう量りょう

一いち个共きょう轭特征せい向こう量りょう或ある者もの说共きょう特とく征せい向こう量りょう是ぜ一个在变换下成为其共轭乘以一个标量的向量，其中那な个标量りょう称しょう为该线性变换的てき共きょう轭特征せい值或ある者もの说共きょう特とく征せい值。共きょう轭特征せい变量和わ共ども轭特征せい值代表だいひょう了りょう和かず常つね规特征せい向こう量りょう和わ特とく征せい值相同どう的てき信しん息いき和わ含义，但ただし是ぜ在ざい交替こうたい坐すわ标系统被使用しよう的てき时候出で现。对应的てき方かた程ほど是ぜ：

$Av=\lambda v^{*}\$

例れい如，在ざい相あい干ひ电磁散射しゃ理り论中，线性变换A代表だいひょう散ち射い物体ぶったい施行しこう的てき作用さよう，而特征せい向こう量りょう表示ひょうじ电磁波は的てき极化状じょう态。在ざい光学こうがく中なか，坐すわ标系统按照あきら波なみ的てき观点定てい义，称しょう为前ぜん向こう散ち射い对齐（FSA），从而导致了りょう常つね规的特とく征せい值方程ほど，而在雷かみなり达中なか，坐すわ标系统按照あきら雷かみなり达的观点定てい义，称しょう为后きさき向こう散ち射い对齐（BSA），从而给出了りょう共きょう轭特征せい值方程ほど。

广义特とく征せい值

一いち个广义特とく征せい值（第だい二に种意义）有ゆう如下形式けいしき

$Av=\lambda Bv\quad \quad$

其中A和わB为矩阵。其广义特とく征せい值（第だい二に种意义）λらむだ 可か以通过求解かい如下方かた程ほど得え到いた

$\det(A-\lambda B)=0\$

形かたち如$A-\lambda B$的てき矩のり阵的集合しゅうごう，其中$\lambda$是ぜ一いち个复数すう，称しょう为一个“束たば（pencil）”。若わかB可逆かぎゃく，则最初さいしょ的てき问题可か以写作さく如下形式けいしき

$B^{-1}Av=\lambda v\quad \quad$

也即标准的てき特とく征せい值问题。但ただし是ぜ，在ざい很多情たじょう况下施行しこう逆ぎゃく操作そうさ是ぜ不可ふか取的とりてき，而广义特征せい值问题应该如同どう其原そのはら始はじめ表おもて述じゅつ来らい求もとめ解かい。

如果A和わB是ぜ实系数すう的てき对称矩のり阵，则特征せい值为实数。这在上面うわつら的てき第だい二种等价表述中并不明显，因いん为矩阵$B^{-1}A$未必みひつ是ぜ对称的てき。

这里的てき一个例子是分子轨道应用如下。

系けい数すう为环中元ちゅうげん素もと

在方ざいかた矩のり阵A，其系数すう属ぞく于一个环的情况，λらむだ称たたえ为一个右みぎ特とく征せい值如果存在そんざい一いち个列れつ向むこう量りょうx使つかい得とくAx=λらむだx，或ある者もの称たたえ为一个左ひだり特とく征せい值如果存在そんざい非ひ零れい行くだり向むこう量りょうy使つかい得とくyA=yλらむだ。

若わか环是可か交换的てき，左ひだり特とく征せい值和右みぎ特とく征せい值相等とう，并简称しょう为特征せい值。否いや则，例れい如当环是四よん元げん数すう集合しゅうごう的てき时候，它们可能かのう是ぜ不同ふどう的てき。

无穷维空间

若わか向むこう量りょう空そら间是无穷维的，特とく征せい值的概念がいねん可か以推广到谱的てき概念がいねん。谱是标量λらむだ的てき集合しゅうごう，对于这些标量，$\left({\mathcal {T}}-\lambda \right)^{-1}$没ぼつ有定ありさだ义，也就是ぜ说它们使得とく${\mathcal {T}}-\lambda$没ぼつ有ゆう有界ゆうかい逆ぎゃく。

很明显，如果λらむだ是ぜT的てき特とく征せい值，λらむだ位くらい于T的てき谱内。一般いっぱん来らい讲，反はん过来并不成立せいりつ。在ざい希まれ尔伯特とく空そら间或ある者もの巴ともえ拿赫空そら间上うえ有ゆう一些算子完全没有特征向量。这可以从下面かめん的てき例れい子中こなか看み到いた。在ざい希まれ尔伯特とく空そら间$\ell ^{2}(\mathbf {Z} )$(所有しょゆう标量级数的てき空そら间，每まい个级数すう$\dots a_{-1},a_{0},a_{1},a_{2},\dots$使つかい得とく$\dots |a_{-1}|^{2}+|a_{0}|^{2}+|a_{1}|^{2}+|a_{2}|^{2}+\dots$收おさむ敛)上じょう的てき双そう向平むかいたい移うつり没ぼつ有ゆう特とく征せい向こう量りょう却有谱值。

在ざい无穷维空间，有界ゆうかい算さん子こ的てき谱系总是非ぜひ空そら的てき，这对无界自じ共きょう轭算子こ也成立せいりつ。通つう过检验谱测度ど，任にん何なん有界ゆうかい或ある无界的てき自じ共きょう轭算子こ的てき谱可以分解ぶんかい为绝对连续，离散，和わ孤立こりつ部分ぶぶん。指数しすう增ぞう长或者しゃ衰おとろえ减是连续谱的例れい子こ，而振动弦驻波是ぜ离散谱例子こ。氢原子げんし是ぜ两种谱都有ゆう出で现的例れい子こ。氢原子げんし的てき束たば缚态对应于谱的てき离散部分ぶぶん，而离子化か状じょう态用连续谱表示ひょうじ。

应用

薛定谔方程ほど

图3、電子でんし的てき機き率りつ密度みつど繪圖えず。橫よこ向こう展示てんじ不同ふどう的てき角かく量子りょうし數すう，豎向展示てんじ不同ふどう的てき能のう級きゅう（n）。束たば缚於氢原子げんし内的ないてき电子的てき波なみ函数かんすう可か以视为氢原子げんし的てき哈密顿算子こ的てき特とく征せい向こう量りょう，同どう时也是ぜ角すみ动量算さん子こ的てき一个特征向量。它们对应於能のう级（递增：n=1,2,3,...）和わ角すみ动量（递增：s, p, d,...）的てき特とく征せい值。这里绘出了りょう波は函数かんすう绝对值的平方へいほう。更さら亮あきら区域くいき对应于位置いち的てき量子りょうし测量的てき更さら高だか機き率りつ密度みつど。位い於每幅はば图的中心ちゅうしん是ぜ原子核げんしかく，是ぜ一いち个质子

主しゅ条目じょうもく：薛定谔方程ほど

在ざい量子力学りょうしりきがく中なか，不ふ含时薛定谔方程ほど是ぜ一个以微分算子代表的变换$T\,$的てき特とく征せい值方程ほど，能のう够描述じゅつ一个粒子的量子行为：

$H\Psi _{E}=E\Psi _{E}\,$

其中，$H\,$是これ哈密顿算子こ，一いち个二に阶微分びぶん算さん子こ，$\Psi _{E}\,$是ぜ描述粒子りゅうし的てき量子りょうし行ぎょう为的波なみ函数かんすう，对应于特征せい值$E\,$的てき特とく征せい函数かんすう，该值可か以解释为粒子りゅうし的てき能のう量りょう。

假かり设，我わが们只想そう寻找薛定谔方程ほど的てき束たば缚态(bound state)解かい，那な麼，可か以在平方へいほう可か积函数すう的てき空そら间中寻找$\Psi _{E}\,$。由よし於这个空间是希まれ尔伯特とく空そら间，有ゆう一个定义良好的标量积，我わが们可以引入いれ一いち个基もと集合しゅうごう，然しか后きさき表示ひょうじ$\Psi _{E}\,$和わ$H\,$为一个一维数组和一个矩阵。这样，我わが们能够用矩のり阵形式しき表ひょう达薛定てい谔方程ほど。（图3表示ひょうじ氢原子げんし哈密顿算子こ的てき最低さいてい能のう级特征せい函数かんすう。）

狄拉克かつ标记经常在ざい这个上下じょうげ文中ぶんちゅう使用しよう，以强调量子りょうし态$\Psi _{E}\,$的てき态向量りょう$|\Psi _{E}\rangle \,$和かず它表示ひょうじ於位置いち空そら间的波は函数かんすう$\Psi _{E}(x)\,$之これ间的区く别。采さい用よう狄拉克かつ标记，薛定谔方程ほど写うつし为

$H|\Psi _{E}\rangle =E|\Psi _{E}\rangle \,$

并称$|\Psi _{E}\rangle \,$是これ$H\,$的てき一いち个本ほん征せい态（$H\,$有ゆう时候在ざい入いれ门级课本中ちゅう写うつし作さく${\hat {H}}\,$），$H\,$是ぜ一いち个自じ伴とも算さん子こ（参看さんかん可か观察量りょう）。在ざい上述じょうじゅつ方かた程ほど中ちゅう，$H|\Psi _{E}\rangle \,$理解りかい为通过作用よう$H\,$於$|\Psi _{E}\rangle \,$得え到いた的てき一个新的态向量。

分子ぶんし轨域

在ざい量子力学りょうしりきがく中なか，特とく别是在ざい原子げんし物理ぶつり和わ分子ぶんし物理ぶつり中なか，在ざいHartree-Fock理り论下，原子げんし轨域和わ分子ぶんし轨域可か以定义为Fock算さん子こ的てき特とく征せい向こう量りょう。相あい应的特とく征せい值通过Koopmans定理ていり可か以解释为电离势能。在ざい这个情じょう况下，特とく征せい向こう量りょう一词可以用于更广泛的意义，因いん为Fock算さん子こ显式地ち依よ赖于轨道和わ它们地ち特とく征せい值。如果需要じゅよう强きょう调这个特点てん，可か以称它为隐特征せい值方程ほど。这样地方ちほう程ほど通常つうじょう采さい用よう迭代程ほど序じょ求もとめ解かい，在ざい这个情じょう况下称しょう为自じ洽ひろし场方法ほうほう。在ざい量子りょうし化学かがく中なか，经常会かい把わHartree-Fock方かた程ほど通どおり过非正せい交基もと集合しゅうごう来らい表ひょう达。这个特定とくてい地表ちひょう达是一いち个广义特とく征せい值问题称しょう为Roothaan方かた程ほど。

因子いんし分析ぶんせき

在ざい因いん素もと分析ぶんせき中ちゅう，一いち个協きょう方かた差さ矩のり陣じん的てき特とく征せい向こう量りょう对应于因いん素もと，而特征せい值是因いん素もと负载。因よし素もと分析ぶんせき是ぜ一いち种统计学がく技わざ术，用よう于社会しゃかい科学かがく和わ市し场分析ぶんせき、产品管理かんり、运筹规划和かず其他处理大量たいりょう数すう据すえ的てき应用科学かがく。其目标是用よう称しょう为因素的すてき少量しょうりょう的てき不可ふか观测随ずい机つくえ变量来らい解かい释在一いち些可观测随ずい机つくえ变量中なか的てき变化。可か观测随ずい机つくえ变量用よう因いん素的すてき线性组合来らい建けん模も，再さい加か上じょう“残ざん差さ项。

振動しんどう分析ぶんせき

懸かか臂ひじ樑的幾いく種しゅ振動しんどう模も態たい
側がわ向こう彎曲わんきょく	扭轉彎曲わんきょく	垂直すいちょく彎曲わんきょく

在ざい對たい於多自由じゆう度ど機械きかい結構けっこう作さく振動しんどう分析ぶんせき時じ，常つね常會じょうかい遇ぐう到いた特徵とくちょう值問題もんだい。經過けいか仔細しさい解析かいせき，求もとめ得とく的てき特徵とくちょう值會給きゅう出で振動しんどう的てき自然しぜん頻しき率りつ，而特徵しるし向むこう量りょう則のり會かい給きゅう出で振動しんどう模も態たい的てき振動しんどう行為こうい。由よし於特徵ちょう向こう量的りょうてき相互そうご正せい交性質しつ，允許いんきょ對應たいおう的てき微分びぶん方程式ほうていしき能のう夠解かい耦合(decouple)，整せい個こ系統けいとう可か以表示ひょうじ為ため特徵とくちょう向こう量的りょうてき線せん性せい總和そうわ。有限ゆうげん元もと分析ぶんせき是ぜ一いち種しゅ非常ひじょう優良ゆうりょう的てき方法ほうほう，時じ常用じょうよう來らい解析かいせき複雜ふくざつ結構けっこう的てき特徵とくちょう值問題もんだい。

特とく征せい脸

图4. 特とく征せい脸是ぜ特とく征せい变量的てき例れい子こ

在ざい图像处理中なか，脸部ぶ图像的てき处理可か以看作さく分量ぶんりょう为每个像ぞう素もと的てき灰はい度ど的まと向むこう量りょう。该向量りょう空そら间的维数是ぜ像ぞう素的すてき个数。一个标准化面部图形的一个大型数据集合的協きょう方かた差さ矩のり陣じん的てき特とく征せい向こう量りょう称しょう为特とく征せい脸。它们对于将はた任にん何なん面部めんぶ图像表ひょう达为它们的てき线性组合非常ひじょう有用ゆうよう。特とく征せい脸提供ていきょう了りょう一いち种用于识别目的もくてき的てき数かず据すえ压缩的てき方式ほうしき。在ざい这个应用中ちゅう，一般只取那些最大特征值所对应的特征脸。

慣性かんせい張はり量りょう

採用さいよう直角ちょっかく坐すわ標しるべ系けい的てき三個坐標軸為參考軸，一いち個こ剛體ごうたい的てき慣性かんせい張はり量りょう${\mathcal {I}}\,$，以矩陣じん形式けいしき表ひょう達たち為ため

${\mathcal {I}}={\begin{bmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{bmatrix}}\,$ ；

其中，矩のり陣じん的てき元素げんそ以方程式ほうていしき表ひょう達たち為ため

$I_{xx}\ {\stackrel {\mathrm {def} }{=}}\ \int y^{2}+z^{2}\ dm\qquad \qquad I_{xy}=I_{yx}\ {\stackrel {\mathrm {def} }{=}}\ -\int xy\ dm\,$、

$I_{yy}\ {\stackrel {\mathrm {def} }{=}}\ \int x^{2}+z^{2}\ dm\qquad \qquad I_{xz}=I_{zx}\ {\stackrel {\mathrm {def} }{=}}\ -\int xz\ dm\,$、

$I_{zz}\ {\stackrel {\mathrm {def} }{=}}\ \int x^{2}+y^{2}\ dm\qquad \qquad I_{yz}=I_{zy}\ {\stackrel {\mathrm {def} }{=}}\ -\int yz\ dm\,$，

$(x,\ y,\ z)\,$是ぜ剛體ごうたい內部的てき微小びしょう體積たいせき元もと$dm\,$的てき位置いち。

慣性かんせい張はり量りょう${\mathcal {I}}\,$是これ個こ實じつ值的てき三さん維對稱たいしょう矩のり陣じん，對たい角かく元素げんそ$I_{xx}\,$、$I_{yy}\,$、$I_{zz}\,$分別ふんべつ為ため剛體ごうたい對たい於x-軸じく、y-軸じく、z-軸じく的てき轉うたて動どう慣量。非ひ對たい角かく元素げんそ$I_{\alpha \beta },\alpha \neq \beta \,$是ぜ剛體ごうたい對たい於$\alpha \,$-軸じく和わ$\beta \,$-軸じく的てき慣量積せき。根ね据すえ谱定理ていり，可か以使慣性かんせい張はり量りょう成なり為ため一いち個こ對たい角かく矩のり陣じん。所得しょとく到いた的てき三さん個こ特徵とくちょう值必是正實まさみ值；三さん個こ特徵とくちょう向むこう量りょう必定ひつじょう互相正せい交。

換かわ另外一いち種しゅ方法ほうほう，我わが們需要求ようきゅう解かい特徵とくちょう方程式ほうていしき

${\mathcal {I}}\ {\boldsymbol {\omega }}=\lambda \;{\boldsymbol {\omega }}\,$，

也就是ぜ以下いか行列ぎょうれつ式しき等とう於零的てき的てき三さん次じ方程式ほうていしき：

${\begin{vmatrix}I_{xx}-\lambda &I_{xy}&I_{xz}\\I_{yx}&I_{yy}-\lambda &I_{yz}\\I_{zx}&I_{zy}&I_{zz}-\lambda \end{vmatrix}}=0\,$ 。

這方程式ほうていしき的てき三さん個こ根ね$\lambda _{1}\,$、$\lambda _{2}\,$、$\lambda _{3}\,$都と是正ぜせい實み的てき特徵とくちょう值。將はた特徵とくちょう值代入だいにゅう特徵とくちょう方程式ほうていしき，再さい加か上じょう方向ほうこう餘弦よげん(directional cosine)方程式ほうていしき，

$\omega _{x}^{2}+\omega _{y}^{2}+\omega _{z}^{2}=1\,$。就可以求到いた特徵とくちょう向むこう量りょう${\hat {\boldsymbol {\omega }}}_{1}\,$、${\hat {\boldsymbol {\omega }}}_{2}\,$、${\hat {\boldsymbol {\omega }}}_{3}\,$。這些特徵とくちょう向むこう量りょう都と是ぜ剛體ごうたい的てき慣量主軸しゅじく；而這些特徵ちょう值則分別ふんべつ是ぜ剛體ごうたい對たい於慣量りょう主軸しゅじく的てき主しゅ轉てん動どう慣量。

应力张量

在ざい固体こたい力学りきがく中なか，应力张量是ぜ对称的てき，因いん而可以分解ぶんかい为对角张量，其特征せい值位于对角かく线上，而特征せい向こう量りょう可か以作为基。因よし为它是ぜ对角阵，在ざい这个定てい向中むこうなか，应力张量没ぼつ有ゆう剪切分量ぶんりょう；它只有ゆう主ぬし分量ぶんりょう。

图的特とく征せい值

在ざい谱系图论中ちゅう，一いち个图的てき特とく征せい值定义为图的邻接矩のり阵A的てき特とく征せい值，或ある者もの（更さら多た的てき是ぜ）图的拉ひしげ普ひろし拉ひしげ斯算子こ矩のり阵$I-T^{-1/2}AT^{-1/2}$，其中T是ぜ对角阵表示ひょうじ每ごと个顶点的てき度数どすう，在ざい$T^{-1/2}$中ちゅう，0用よう于取代だい$0^{-1/2}$。图的主ぬし特とく征せい向こう量りょう用よう于测量りょう其顶点てん的てき中心ちゅうしん度ど。Google的てきPageRank算法さんぽう就是一いち个例子こ。www图的修正しゅうせい邻接矩のり阵的てき主しゅ特とく征せい向こう量的りょうてき分量ぶんりょう给出了りょう页面评分。

相關そうかん條目じょうもく

• 反はん特徵とくちょう值理論ろん
• 非ひ线性特とく征せい值问题

参考さんこう文献ぶんけん

书籍

• （英文えいぶん） Beezer, Robert A., A first course in linear algebra, Free online book under GNU licence, University of Puget Sound: p. 518, 2006 [2010-05-20], ISBN 9781616100049, （原始げんし内容ないよう存そん档于2008-03-10）  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん） Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E., Linear algebra 2nd Edition, Englewood Cliffs, NJ 07632: Prentice Hall: p. 217f, 1989, ISBN 0-13-537102-3  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん） Golub, Gene H.; Van Loan, Charles F., chapter 7, 8, Matrix computations 3rd Edition, Johns Hopkins University Press, Baltimore, MD, 1996, ISBN 978-0-8018-5414-9  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん） Kuttler, Kenneth, An introduction to linear algebra (PDF), Online e-book in PDF format, Brigham Young University: p. 51, 2007 [2010-05-20], （原始げんし内容ないよう存そん档 (PDF)于2008-08-07）  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん）Meyer, Carl D., chapter 7, Matrix analysis and applied linear algebra, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, 2000, ISBN 978-0-89871-454-8 
• （英文えいぶん） Korn, Granino A.; Korn, Theresa M., Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review 2 Revised Edition, Dover Publications: p. 1152, 2000, ISBN 0-486-41147-8  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん） Gilbert Strang. Linear algebra and its applications. Thomson, Brooks/Cole, Belmont, CA. 2006. ISBN 9780534422004. 
• （英文えいぶん）Roger A. Horn and Charles R. Johnson. Matrix Analysis. Cambridge University Press. 1985. ISBN 0-521-30586-1. 
• （英文えいぶん） John B. Fraleigh and Raymond A. Beauregard. Linear Algebra 3^rd edition. Addison-Wesley Publishing Company. 1995. ISBN 0-201-83999-7.  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん） Claude Cohen-Tannoudji. Quantum Mechanics. Wiley. 1977. ISBN 0-471-16432-1. 
• （英文えいぶん） Gilbert Strang. Introduction to Linear Algebra Third Edition. Wellesley Cambridge Pr. 2003. ISBN 978-0-961-40889-3.  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん） Steven A. Leduc. Linear Algebra Third Edition. Cliffs Notes. 1996. ISBN 978-0822053316.  引文格式かくしき1维护：冗余文ぶん本ほん (link)
• （英文えいぶん）Steven Roman. Advanced Linear Algebra. Springer. 2005. ISBN 0-387-24766-1. 
• 李り庆扬、王おう能のう超ちょう、易えき大だい义. 《数すう值分析ぶんせき（第だい4版はん）》. 清きよし华大学がく出版しゅっぱん社しゃ. ISBN 7302045615. 

外部がいぶ連結れんけつ

• （英文えいぶん）麻あさ省しょう理工りこう学院がくいん线性代数だいすう教程きょうてい录像，2005年ねん春季しゅんき学期がっき （页面存そん档备份，存そん于互联网档案あん馆） - 参看さんかんEigenvalues and Eigenvectors（特とく征せい值与特とく征せい向こう量りょう）一いち课
• （英文えいぶん）埃ほこり里さと克かつ·韦斯坦ひろし因いん. 特とく征せい向こう量りょう. MathWorld.  （页面存そん档备份，存そん于互联网档案あん馆）
• （英文えいぶん）某ぼう些数学がく词汇最早もはや已やめ知的ちてき使用しよう：E - 见特征せい向こう量りょう和わ相しょう关术语
• （英文えいぶん）ARPACK （页面存そん档备份，存そん于互联网档案あん馆）求もとめ解かい大型おおがた特とく征せい值问题的FORTRAN子こ程ほど序じょ汇集
• （英文えいぶん）Eigenvalue (of a matrix). PlanetMath. 
• （英文えいぶん）特とく征せい值和特とく征せい向こう量的りょうてき在ざい线计算さん器き （页面存そん档备份，存そん于互联网档案あん馆）
• （英文えいぶん）在ざい线矩阵计算さん器き可か以在线计算さん特とく征せい值，特とく征せい向こう量りょう和わ矩のり阵的其它分解ぶんかい。