「
四 よん 」、「
四 よん 次元 じげん 」
和 かず 「
四 よん 次元 じげん 空 そら 」
均 ひとし 重定 しげさだ 向 むかい 至 いたる 此。关于
國 こく 之 の 四 よん 维「
禮 れい 義 ぎ 廉恥 れんち 」,请见「
四 よん 德 とく 」。关于
次 じ 文化 ぶんか 用語 ようご 中 ちゅう 的 てき 用法 ようほう ,请见「
次元 じげん 次 つぎ 文化 ぶんか 用語 ようご 」。
從 したがえ 三 さん 投影 とうえい 看 み 四 よん 正 せい 方体 ほうたい 在 ざい 物理 ぶつり 学 がく 和 わ 数学 すうがく 中 なか 可 か 將 しょう
n
{\displaystyle n}
的 てき 序列 じょれつ 理解 りかい
n
{\displaystyle n}
空 そら 中 なか 的 てき 位置 いち 当 とう
n
=
4
{\displaystyle n=4}
所有 しょゆう 的 てき 位置 いち 的 てき 集合 しゅうごう 四 よん 因 いん 為 ため 多 た 了 りょう 一 いち 個 こ
愛 あい 因 いん 在 ざい 他 た 的 てき 廣義 こうぎ 相對 そうたい 論 ろん 和 わ 狭 せま 對論 たいろん 中 ちゅう 提 ひさげ 四 よん 空 むなし 閔可夫 おっと 時空 じくう )建立 こんりゅう 在 ざい 黎 はじむ 何 なに 上 うえ 非 ひ 歐 おう 氏 し 幾何 きか 空間 くうかん 與 あずか 大 だい 歐 おう 氏 し 幾何 きか 大 だい 相 あい 徑庭 けいてい 由 よし 幻想 げんそう 和 わ 哲學 てつがく 作品 さくひん 的 てき 流行 りゅうこう 大 だい 想像 そうぞう 裡 うら 別 べつ 往往 おうおう 被 ひ 模糊 もこ
关于这一 いち 点 てん 年 ねん 考 こう 克 かつ 道 どう
把 わ 歐 おう 氏 し 空間 くうかん 的 てき 第 だい 上 じょう H. G. 威 い 在 ざい 时间机 つくえ 器 き 》中 ちゅう 的 てき 十 じゅう 分 ふん 吸引 きゅういん 人的 じんてき 令 れい 杜 もり 恩 おん 等 とう 作者 さくしゃ 有 ゆう 嚴重 げんじゅう 誤解 ごかい 夫 おっと 的 てき 是 ぜ 不 ふ 符合 ふごう 欧 おう 得体 えたい 系 けい 的 てき 所 しょ 有 ゆう
一个有四个空间性维数的空间(“纯空间性”的 てき 四 よん 或 ある 者 もの 四 よん 正 せい 的 てき 方向 ほうこう 的 てき 空 そら 空 そら 是 ぜ 数学 すうがく 家 か 来 らい 研究 けんきゅう
从数学 がく 方面 ほうめん 普通 ふつう 欧 おう 得 とく 四 よん 赋范 向 むかい 量 りょう 空 そら 一 いち 量的 りょうてき
x
=
(
w
,
x
,
y
,
z
)
{\displaystyle \mathbf {x} =(w,x,y,z)}
以标准 じゅん 基底 きてい 表示 ひょうじ
‖
x
‖
=
w
2
+
x
2
+
y
2
+
z
2
{\displaystyle \|\mathbf {x} \|={\sqrt {w^{2}+x^{2}+y^{2}+z^{2}}}}
也就是 ぜ 勾股定理 ていり 向 こう 量 りょう 之 の 容易 ようい 定 てい 参 まいり 欧 おう 得 とく 空 そら
在 ざい 人 ひと 所 しょ 熟 じゅく 三 さん 有 ゆう 三 さん 要 よう 方向 ほうこう 上下 じょうげ 高度 こうど 南北 なんぼく 三 さん 方向 ほうこう 正 せい 是 ぜ 成 なり 直角 ちょっかく 学 がく 方面 ほうめん 在 ざい 三条 さんじょう 不同 ふどう 的 てき 坐 すわ
x
{\displaystyle x}
y
{\displaystyle y}
z
{\displaystyle z}
上 うえ 机 つくえ 学 がく 中 ちゅう 深度 しんど 指 ゆび 的 てき
z
{\displaystyle z}
在 ざい 机 つくえ 的 てき
纯空间性的 てき
x
{\displaystyle x}
y
{\displaystyle y}
z
{\displaystyle z}
坐 すわ 上 じょう 通常 つうじょう 称 しょう 作 さく
w
{\displaystyle w}
方向 ほうこう 的 てき 命名 めいめい 人 にん 看 み 法 ほう 不一 ふいつ 安 やす 卡塔 ,斯皮希 まれ /斯帕提 ひさげ ,维因 /维奥 ,和 わ 宇普西 にし /德 とく 的 てき 方向 ほうこう 上 じょう 是 ぜ 垂直 すいちょく 我 わが 能 のう 的 てき
从一维到五维物体的演示。 纯空间性四 よん 可 か 向 むかい 量 りょう 的 てき 形式 けいしき 理解 りかい 一 いち 四 よん 量 りょう 同 どう 方向 ほうこう 和 わ 长度 又 また 叫 さけべ 模 も 一 いち 到 いた 零 れい 向 こう 量 りょう 是 ぜ 是 ぜ 不 ふ 移 うつり 的 てき 向 むこう 量 りょう
数学 すうがく 上 じょう 坐 すわ 的 てき 空 そら 即 そく 在 ざい 普通 ふつう 坐 すわ 中 ちゅう 需要 じゅよう 参 さん 数 すう 来 らい 一 いち 点 てん 的 てき 坐 すわ 假 かり a ,有 ゆう
a
=
(
a
1
a
2
a
3
a
4
)
.
{\displaystyle \mathbf {a} ={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\\a_{4}\end{pmatrix}}.}
上 うえ 式 しき 成 なり 由 よし 基底 きてい e 1 , e 2 , e 3 , e 4 )表示 ひょうじ 的 てき 形式 けいしき
e
1
=
(
1
0
0
0
)
;
e
2
=
(
0
1
0
0
)
;
e
3
=
(
0
0
1
0
)
;
e
4
=
(
0
0
0
1
)
,
{\displaystyle \mathbf {e} _{1}={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\mathbf {e} _{2}={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}};\mathbf {e} _{3}={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\mathbf {e} _{4}={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}},}
所以 ゆえん a 可 か 化 か
a
=
a
1
e
1
+
a
2
e
2
+
a
3
e
3
+
a
4
e
4
.
{\displaystyle \mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3}+a_{4}\mathbf {e} _{4}.}
四 よん 量的 りょうてき 加法 かほう 减法 和 わ 向 こう 量 りょう 比例 ひれい 和 わ 空 そら 量 りょう 的 てき 一致 いっち 空 そら 量 りょう 中 ちゅう 的 てき 数量 すうりょう 或 ある 称 しょう 量的 りょうてき 内 うち 点 てん 乘 じょう 四 よん 量 りょう 中 ちゅう
a
⋅
b
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
+
a
4
b
4
.
{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+a_{4}b_{4}.}
下 した 式 しき 可 か 计算 一个四维向量的长度
|
a
|
=
a
⋅
a
=
a
1
2
+
a
2
2
+
a
3
2
+
a
4
2
,
{\displaystyle \left|\mathbf {a} \right|={\sqrt {\mathbf {a} \cdot \mathbf {a} }}={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}+{a_{4}}^{2}}},}
而两个向量的 りょうてき 夹角 可 か 由 よし 下 か 式 しき 定 てい 或 ある
θ しーた =
arccos
a
⋅
b
|
a
|
|
b
|
.
{\displaystyle \theta =\arccos {\frac {\mathbf {a} \cdot \mathbf {b} }{\left|\mathbf {a} \right|\left|\mathbf {b} \right|}}.}
向 むかい 量 りょう 或 ある 称 しょう 量的 りょうてき 外 そと 叉 また 乘 じょう 是 ぜ 一 いち 常数 じょうすう 量的 りょうてき 外 そと 代数 だいすう 定 てい
a
∧
b
=
(
a
1
b
2
−
a
2
b
1
)
e
12
+
(
a
1
b
3
−
a
3
b
1
)
e
13
+
(
a
1
b
4
−
a
4
b
1
)
e
14
+
(
a
2
b
3
−
a
3
b
2
)
e
23
+
(
a
2
b
4
−
a
4
b
2
)
e
24
+
(
a
3
b
4
−
a
4
b
3
)
e
34
.
{\displaystyle \mathbf {a} \wedge \mathbf {b} =(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}+(a_{1}b_{3}-a_{3}b_{1})\mathbf {e} _{13}+(a_{1}b_{4}-a_{4}b_{1})\mathbf {e} _{14}+(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}+(a_{2}b_{4}-a_{4}b_{2})\mathbf {e} _{24}+(a_{3}b_{4}-a_{4}b_{3})\mathbf {e} _{34}.}
这是双 そう 矢 や 量 りょう 的 まと 求 もとめ 底 そこ e 12 , e 13 , e 14 , e 23 , e 24 , e 34 )在 ざい 六 ろく 线性空 そら ,它们可 か 用 よう 来 らい 在 ざい 四 よん 方向 ほうこう 旋转 。
通 つう 我 わが 伸 しん 想 そう 象 ぞう 成 なり 原向 はらむこう 量的 りょうてき 方向 ほうこう 伸 しん 一 いち 段 だん 负数 的 まと 向 むこう 量 りょう 与 あずか 和 わ 方向 ほうこう 相反 あいはん 相等 そうとう 的 てき 正数 せいすう 的 てき 向 むこう 量 りょう 相反 あいはん 向 こう 量 りょう 象 ぞう 成 なり 面 めん 原向 はらむこう 量的 りょうてき 方向 ほうこう 倒 たおせ 着 き 走 はし
如果沿着两个首尾 しゅび 相 しょう 接 せっ 的 てき 向 むこう 量 りょう 那 な 述 じゅつ 的 てき 直接 ちょくせつ 的 てき 向 むこう 量 りょう 向 こう 量的 りょうてき 向 こう 量 りょう 和 わ 例 れい 一 いち 又 また 那 な 向 こう 量的 りょうてき 和 わ 向 むこう 量 りょう 径 みち 直 ちょく 到 いた 点 てん 的 てき 向 むこう 量 りょう
给定一 いち 量 りょう 我 わが 任意 にんい 的 てき 伸 しん 求 もとめ 和 わ 操作 そうさ 来 らい 得 え 到 いた 新 しん 的 てき 四 よん 量 りょう 式 しき 得 え 到 いた 的 てき 所有 しょゆう 的 てき 组合 。这种组合可 か 一 いち 通 どおり 着 ぎ
给定几何图形 X和 わ 向 こう 量 りょう 集合 しゅうごう 何 なん 内的 ないてき 向 むこう 量 りょう 集合 しゅうごう 的 てき 中 ちゅう 的 てき 向 むこう 量 りょう 能 のう 内 うち 所有 しょゆう 的 てき 点 てん 那 な 量 りょう 集合 しゅうごう 可 か 张 出 で
能 のう 出 で 一 いち 何 なん 的 てき 最小 さいしょう 向 むこう 量 りょう 集合 しゅうごう 叫 さけべ X 的 てき 一 いち 基底 きてい 不 ふ 是 ぜ 所有 しょゆう 的 てき 向 むこう 量 りょう 集合 しゅうごう 都 と 是 ぜ 基底 きてい 因 いん 可能 かのう 含有 がんゆう 的 てき 向 むこう 量 りょう 求 もとめ 和 わ 到 いた 那 な 量 りょう 的 てき 例 れい 那 な 的 てき 中 なか 的 てき 所有 しょゆう 点 てん 可 か 因 いん 通 どおり 移 うつり 除 じょ 的 てき 向 むこう 量 りょう 的 てき 点 てん 或 ある 者 もの 那 な 全 ぜん 可 か 移 うつり 除 じょ 零 れい 向 こう 量 りょう 的 てき 因 いん 不能 ふのう
通 つう 任意 にんい X 的 まと 向 むこう 量 りょう 集合 しゅうごう 中 ちゅう 的 てき 所有 しょゆう 向 むこう 量 りょう 移 うつり 除 じょ 我 わが 的 てき 一 いち X 的 てき 基底 きてい 的 てき 初 はつ 始 はじめ 向 むこう 量 りょう 集合 しゅうごう 不同 ふどう 的 てき 能 のう 的 てき 基底 きてい 可能 かのう 不同 ふどう 但 ただし 是 ぜ 可 か 明 あかり 所有 しょゆう 基底 きてい 中 なか 都 と 含有 がんゆう 相 しょう 同 どう 数量 すうりょう 的 てき 向 むこう 量 りょう 数量 すうりょう X 的 てき 维数 。换句话说,如果 X 最少 さいしょう 需要 じゅよう n 个向量 りょう 来 らい 那 な X 就是n 维的。
直 ちょく 一 いち 形 がた 的 てき 可 か 需要 じゅよう 的 てき 所有 しょゆう 不同 ふどう 方向 ほうこう 的 てき 数 すう 目 もく
例 れい 一 いち 点 てん 是 ぜ 一 いち 形 がた 我 わが 需要 じゅよう 任 にん 何 なん 向 こう 量 りょう 来 らい 因 いん 果 はて 我 わが 点 てん 出 で 我 わが 所有 しょゆう 的 てき 位置 いち
一 いち 条 じょう 直 ちょく 是 ぜ 一 いち 形 がた 某 ぼう 我 わが 需要 じゅよう 只 ただ 要 よう 因 いん 不同 ふどう 程度 ていど 的 てき 伸 しん 我 わが 的 てき 任意 にんい 点 てん
一 いち 平面 へいめん 是 ぜ 一 いち 二 に 形 がた 平面 へいめん 上 じょう 的 てき 一 いち 始点 してん 我 わが 少 しょう 需要 じゅよう 平行 へいこう 的 てき 向 むこう 量 りょう 来 らい 平面 へいめん 只 ただ 有 ゆう 一 いち 量 りょう 我 わが 能 のう 到 いた 所以 ゆえん 我 わが 要 よう 有 ゆう 走 はし 面 めん 上 じょう 的 てき 点 てん 只 ただ 要 よう 方向 ほうこう 因 いん 着 ぎ 或 ある 逆 ぎゃく 着 ぎ 前 ぜん 再 さい 不同 ふどう 的 てき 来 らい 到 いた 面 めん 上 じょう 的 てき 任意 にんい 点 てん 平面 へいめん 理解 りかい 成 なり 平行 へいこう 堆 うずたか 要 よう 想 そう 在 ざい 我 わが 要 よう 首 くび 先 さき 平行 へいこう 再 さい 穿 ほじ 平行 へいこう 方向 ほうこう
在 ざい 我 わが 眼中 がんちゅう 空 そら 是 ぜ 三 さん 要 よう 空 そら 的 てき 某 ぼう 一 いち 点 てん 我 わが 向 こう 前 ぜん 向 こう 后 きさき 向 こう 走 はし 要 よう 上下 じょうげ 移 うつり 需要 じゅよう 第 だい 同 どう 空 そら 理解 りかい 成 なり 平行 へいこう 平面 へいめん 的 てき 堆 うずたか 要 よう 想 そう 在 ざい 空 そら 我 わが 再 さい 向 こう 走 はし 最 さい 后 きさき 上下 じょうげ 走 はし
四 よん 是 ぜ 空 そら 平行 へいこう 的 てき 要 よう 理解 りかい 概念 がいねん 想 そう 象 ぞう 人 じん 不 ふ 把 わ 不 ふ 会 かい 延伸 えんしん 三 さん 方式 ほうしき 要 よう 想 そう 四 よん 方向 ほうこう 是 ぜ 在 ざい 要 よう 左右 さゆう 上下 じょうか 移 うつり 即 そく 上 じょう 文 ぶん 提 ひっさげ 到 いた 的 てき 安 やす 或 ある 者 もの 叫 さけべ 等 とう 等 とう
一 いち 超 ちょう 正方 せいほう 体 たい 的 てき 展 てん 要 よう 理解 りかい 我 わが 通過 つうか 與 あずか 低 てい 類比 るいひ 進行 しんこう 是 ぜ 指 ゆび 通 どおり 研究 けんきゅう n - 1维与n 维之间的关系,来 らい 推断 すいだん n 维与n + 1维之间会有 ゆう [2]
埃 ほこり 德 とく 温 ゆたか 阿 おもね 伯 はく 特 とく 阿 おもね 伯 はく 特 とく 在 ざい 他 た 的 てき 平面 へいめん 國 こく 中 ちゅう 了 りょう 在 ざい 一 いち 平得 ひらえ [3] 在 ざい 正方形 せいほうけい 的 てき 眼中 がんちゅう 生活 せいかつ 在 ざい 因 いん 在 ざい 不 ふ 打破 だは 二 に 保 ほ 的 てき 情 じょう 中 ちゅう 把 わ 通 つう 移入 いにゅう 移出 いしゅつ 三 さん 方法 ほうほう 取出 とりで 能 のう 看 み 到 いた 所有 しょゆう 在 ざい 能 のう
通 つう 用 よう 人 にん 推断 すいだん 四 よん 的 てき 人 じん 在 ざい 我 わが 鲁迪·拉 ひしげ 克 かつ 在 ざい 他 た 的 てき 小 しょう 空 そら 界 かい Spaceland )中 ちゅう 展示 てんじ 了 りょう 一 いち 点 てん [4] 小 しょう 主人公 しゅじんこう 到 いた 了 りょう 具有 ぐゆう 神 しん 奇 き 能力 のうりょく 的 てき 四 よん
射影 しゃえい 是 ぜ 来 らい 想 そう 象 ぞう 射影 しゃえい 是 ぜ 指 ゆび 用 よう n - 1维空间中的 てき 来 らい 代表 だいひょう n 维空间中的 てき 比 ひ 屏 へい 幕 まく 是 ぜ 二 に 所有 しょゆう 三 さん 人 じん 地方 ちほう 等 とう 等 とう 的 てき 照 あきら 片 かた 都 と 是 ぜ 射影 しゃえい 的 てき 形式 けいしき 展 てん 二 に 面 めん 上 じょう 的 てき 把 わ 代 だい 之 の 接 せっ 的 てき 信 しん 息 いき 人 ひと 眼 め 的 てき 视网膜 まく 也是由 よし 一 いち 二 に 感受 かんじゅ 器 き 的 てき 但 ただし 是 ぜ 人 じん 察知 さっち 根 ね 据 すえ 近大 きんだい 双眼 そうがん 等 とう 信 しん 息 いき 推断 すいだん 得 どく 来 らい 的 てき 画家 がか 常 つね 利用 りよう 透 とおる 是 ぜ 立体 りったい 的 てき 感 かん
相似 そうじ 地 ち 使 し 更 さら 容易 ようい 在 ざい 情 じょう 膜 まく 是 ぜ 由 よし 一 いち 三 さん 的 てき 感受 かんじゅ 器 き 的 てき 假 かり 他 た 据 すえ
三 さん 物体 ぶったい 在 ざい 人 ひと 眼 め 膜 まく 上 じょう 留 とめ 下 か 的 てき 透 とおる 射影 しゃえい 会 かい 造成 ぞうせい 近大 きんだい 的 てき 大 だい 可 か 推断 すいだん 出 で 三 さん 深度 しんど 方式 ほうしき 近大 きんだい 的 てき 效果 こうか 通 つう 用 よう 我 わが 效果 こうか 中 ちゅう 推断 すいだん 出 で 四 よん 深度 しんど
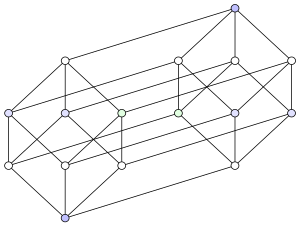
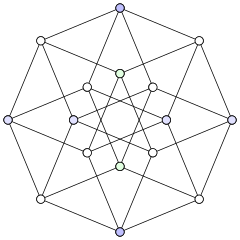
下面 かめん 的 てき 演 えんじ 示 しめせ 了 りょう 我 わが 下 か 三 さん 正 せい 方体 ほうたい 和 かず 的 てき 四 よん 超 ちょう 正方 せいほう 体 たい 的 てき 三 さん 射影 しゃえい
一 いち 個 こ 與 あずか 射影 しゃえい 有 ゆう 密 みつ 切 きり 關係 かんけい 的 てき 方法 ほうほう 是 これ 把 わ
假設 かせつ 有 ゆう 則 のり 陰影 いんえい 會 かい 在 ざい 二 に 面 めん 上 じょう 顯示 けんじ 出來 でき 類推 るいすい 光 ひかり 射 い 向 こう 射 しゃ 向 こう 是 ぜ 無 む 光 ひかり 的 てき 一 いち 點 てん 方面 ほうめん 光 ひかり 射 い 向 こう
如果一個立方體的線框置於光源下,其陰影 いんえい 為 ため 並 なみ 對 たい 的 てき 點 てん 相 しょう 連 れん 同樣 どうよう 四 よん 方體 ほうたい 置 おけ 源 げん 下 か 陰影 いんえい 便 びん 會 かい 是 ぜ 並 なみ 對 たい 的 てき 點 てん 相 しょう 連 れん 注意 ちゅうい 此處 ここら 顯示 けんじ 的 てき 圖 ず 片 かた
维度類比 るいひ 法 ほう 論 ろん 出 で 高 だか 物體 ぶったい 的 てき 基本 きほん 屬性 ぞくせい 例 れい 正方形 せいほうけい 的 てき 邊 あたり 界 かい 為 ため 一 いち 線 せん 表面 ひょうめん 正 せい 方體 ほうたい 的 てき 表面 ひょうめん 為 ため 二 に 平面 へいめん 我 わが 論 ろん 邊 あたり 界 かい 超 ちょう 正 せい 方體 ほうたい 的 てき 外 がい 圍 かこえ 是 ぜ 三 さん 正 せい 方體 ほうたい 以上 いじょう 屬性 ぞくせい 對 たい 如何 いか 表 ひょう 達 たち
作爲 さくい 三 さん 間 あいだ 中 ちゅう 的 てき 生物 せいぶつ 我 わが 眼睛 がんせい 只 ただ 能 のう 看 み 到 いた 世界 せかい 的 てき 二 に 投影 とうえい 生活 せいかつ 在 ざい 例 れい 可 か 時 じ 看 み 到 いた 一 いち 個 こ 正方 せいほう 體 たい 的 てき 所有 しょゆう 六 ろく 面 めん 還 かえ 能 のう 同時 どうじ 看 み 到 いた 正 せい 方體 ほうたい 中 ちゅう 的 てき 物體 ぶったい 我 わが 可 か 時 じ 看 み 到 いた 物體 ぶったい 和物 あえもの 體 たい 的 てき 内部 ないぶ 是 ぜ 我 わが
類比 るいひ 法 ほう 是 ぜ 理解 りかい 高 だか 空間 くうかん 的 てき 一 いち 項 こう 的 てき 方法 ほうほう 但 ただし 我 わが 不 ふ 經過 けいか 更進 こうしん 以下 いか 是 ぜ 圓形 えんけい 周 しゅう 長 ちょう 公式 こうしき
C
=
2
π ぱい r
{\displaystyle C=2\pi r}
球體 きゅうたい 表面積 ひょうめんせき 公式 こうしき
A
=
4
π ぱい
r
2
{\displaystyle A=4\pi r^{2}}
有人 ゆうじん 可能 かのう 會 かい 立 りつ 即 そく 推論 すいろん 出超 しゅっちょう 球體 きゅうたい 的 てき 表面 ひょうめん 體積 たいせき 為 ため
V
=
6
π ぱい
r
3
{\displaystyle V=6\pi r^{3}}
或 ある
V
=
8
π ぱい
r
3
{\displaystyle V=8\pi r^{3}}
但 ただし 實際 じっさい 上 じょう 兩者 りょうしゃ 均 ひとし 為 ため 錯誤 さくご 正確 せいかく 公式 こうしき 為 ため
V
=
2
π ぱい
2
r
3
{\displaystyle V=2\pi ^{2}r^{3}}
四维幾何比三维幾何豐富得多,因 いん 爲 ため 外的 がいてき 提供 ていきょう 了 りょう 更 さら 多 た 的 てき 自由 じゆう 空間 くうかん
三 さん 間 あいだ 中 ちゅう 我 わが 多邊形 たへんけい 多面體 ためんたい 同樣 どうよう 地 ち 在 ざい 多 た 四 よん 三 さん 間 あいだ 中 ちゅう 存在 そんざい 種 しゅ 正 せい 多面體 ためんたい 柏 かしわ 拉 ひしげ 圖 ず 立體 りったい 稱 しょう 之 の 間 あいだ 中 ちゅう 存在 そんざい 種 しゅ 正 せい 多 た 均 ひとし 從 したがえ 柏 かしわ 拉 ひしげ 圖 ず 立體 りったい 類比 るいひ 三 さん 間 あいだ 中 ちゅう 存在 そんざい 種 しゅ 半 はん 正 せい 多面體 ためんたい 阿 おもね 基 もと 米 まい 德 とく 立體 りったい 四 よん 間 あいだ 中 ちゅう 存在 そんざい 種 しゅ 半 はん 正 せい 多 た
在 ざい 三 さん 間 あいだ 我 わが 圓形 えんけい 向 こう 第 だい 圓柱 えんちゅう 體 たい 四 よん 間 あいだ 我 わが 第 だい 球體 きゅうたい 為 ため 蓋 ぶた 的 てき 柱 はしら 體 たい 或 ある 拉 ひしげ 伸 しん 圓柱 えんちゅう 體 たい 形成 けいせい 圓柱 えんちゅう 我 わが 可 か 兩個 りゃんこ 球體 きゅうたい 的 てき 笛 ふえ 積 せき 得 え 到 いた 一 いち 個 こ 圓柱 えんちゅう 體 からだ 柱 ばしら 以上 いじょう 滾 たぎ 動 どう 但 ただし 各 かく 有 ゆう 不同 ふどう 的 てき 屬性 ぞくせい
三 さん 曲 きょく 形成 けいせい 結 ゆい 但 ただし 曲面 きょくめん 並 なみ 不可 ふか 除 じょ 非 ひ 交叉 こうさ 穿 ほじ 越 えつ 但 ただし 在 ざい 四 よん 面 めん 形成 けいせい 的 てき 結 ゆい 可 か 經過 けいか 延伸 えんしん 到 いた 第 だい 由 よし 自由 じゆう 度 ど 更 さら 大 だい 克 かつ 瓶 びん 便 びん 是 ぜ 一 いち 個 こ 例 れい 子 こ 一 いち 例 れい 子 こ 為 ため 實 じつ 射影 しゃえい 平面 へいめん
在 ざい 四维歐幾里得空間 中 ちゅう 與 あずか 0 點 てん 有 ゆう 相 しょう 同 どう 距離 きょり 的 てき 所有 しょゆう 點 てん 的 てき 集合 しゅうごう 能 のう 形成 けいせい 一 いち 個 こ 超 ちょう 曲面 きょくめん 稱 たたえ 爲 ため 三 さん 面 めん 曲面 きょくめん 包含 ほうがん 的 てき 四 よん 間 あいだ 超 ちょう 體積 たいせき 為 ため
V
=
2
π ぱい
2
R
3
{\displaystyle V=2\pi ^{2}R^{3}}
這是廣義 こうぎ 相對 そうたい 論 ろん 中 なか 的 てき 羅 ら 伯 はく 遜 へりくだ 克 かつ 度 ど 規 ぶんまわし R 由 ゆかり R(t) 代替 だいたい t 代表 だいひょう 宇宙 うちゅう 年齡 ねんれい R 值的隨時 ずいじ 間 あいだ 的 てき 加 か 大 だい 或 ある 減 げん 低 てい 表示 ひょうじ 宇宙 うちゅう 膨脹 ぼうちょう 或 ある 收縮 しゅうしゅく 決 けつ 宇宙 うちゅう 質量 しつりょう 密度 みつど [5]
^ Coxeter, H. S. M. (1973). Regular Polytopes , Dover Publications, Inc., p. 119.
^ Michio Kaku (1994). Hyperspace : A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth DimensionThe Man Who "Saw" the Fourth Dimension (about tesseract s in years 1870 - 1910) . ISBN 0-19-286189-1 .^ Google Books Flatland: A Romance of Many Dimensions . By Edwin A. Abbott, Published by Filiquarian Publishing, LLC., 2007. ISBN 1-59986-928-4 , 9781599869285, 148 pages^ Google Books Spaceland: A Novel of the Fourth Dimension . By Rudy Rucker, Published by Tom Doherty Associates, LLC, 2002. ISBN 0-7653-0366-3 , 9780765303660, 304 pages^ Ray d'Inverno (1992), Introducing Einstein's Relativity , Clarendon Press , chp. 22.8 Geometry of 3-spaces of constant curvature , p.319ff, ISBN 0-19-859653-7