维基百科,自由的百科全书
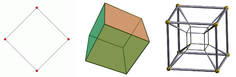 从左到右:正方形,立方体和超立方体。二维(2D)正方形的边界为一维(1D)线;三维(3D)立方体由二维面积;和四维(4D)超立方体由三维体积。在屏幕等二维表面上显示,三维立方体和4D立方体需要投影。
从左到右:正方形,立方体和超立方体。二维(2D)正方形的边界为一维(1D)线;三维(3D)立方体由二维面积;和四维(4D)超立方体由三维体积。在屏幕等二维表面上显示,三维立方体和4D立方体需要投影。
 以二维图像表示的前四个空间维度。
以二维图像表示的前四个空间维度。
 0維是一點,1維是線,2维是一個長和寬(或曲線)面積,3维是2维加上高度形成體積面,4維則是建立在2維之上又多一個參數
0維是一點,1維是線,2维是一個長和寬(或曲線)面積,3维是2维加上高度形成體積面,4維則是建立在2維之上又多一個參數
维度(英語:Dimension),又稱维数、量纲和次元(日语:次元/じげん),是描述对象状态所需的独立参数(数学)或系统自由度(物理)的数量。在物理学和数学中,数学空间的维数被非正式地定义为指定其中任何点所需的最小坐标数[1][2]。
0维是一點,沒有長度。1维是線,只有長度。2维是一個平面,是由長度和寬度(或曲線)形成面積。3维是2维加上高度形成「體積面」。雖然在一般人中習慣了整數维,但在碎形中維度不一定是整數,可能会是一个非整的有理数或者无理数。
三維空間中一共有3个维度(上下、前后、左右)。在三維空間中可以往上下、前後、左右移動,其他方向的移動只需用3個三维空間軸來表示。向下移就等於負方向地向上移,向左前移就只是向左和向前移的混合。
在物理學上時間是第四维,與三個空間维不同的是,它只有一個,且只能往一方向前進。
我们所居於的时空有四个维(3个空间轴和1个时间轴),根據愛因斯坦的概念稱為四维时空,我們的宇宙是由時间和空间構成,而這條時間軸是一條虛數值的軸。
弦理論認為我們所居於的宇宙實際上有更多的維度(通常10、11或26個)。但是這些附加的维度所量度的是次原子大小的宇宙。
维度是理论模型,在非古典物理学中这点更为明显。所以不用计较宇宙的维数是多少,只要方便描述就行了。
在物理學中,質的量纲通常以質的基本單位表示:例如,速率的量纲就是長度除以時間。






