惠 めぐみ 特 とく 尼 あま 定理 ていり 概 がい 述 じゅつ 图论 中 なか 惠 めぐみ 特 とく 尼 あま 定理 ていり 英語 えいご Whitney's theorem ),又 また 称 たたえ 惠 めぐみ 特 とく 尼 あま 性 せい 定理 ていり Whitney's theorem on connectivity )[ 1] 是 ぜ 美國 びくに 數學 すうがく 家 か 哈斯勒·惠 めぐみ 特 とく 尼 あま 于1932年 ねん [ 2] 提出 ていしゅつ 的 てき 2连通图 等 とう 定理 ていり 定理 ていり 提供 ていきょう 了 りょう 不 ふ 同点 どうてん 性 せい 画 が 了 りょう 特殊 とくしゅ 性 せい [ 3]
对一个图
G
{\displaystyle G}
若 わか
G
{\displaystyle G}
至 いたり 少 しょう 存在 そんざい
G
{\displaystyle G}
是 ぜ 的 てき 当 とう 当 とう
G
{\displaystyle G}
中 ちゅう 任意 にんい 点 てん
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
中 ちゅう 至 いたり 少 しょう 存在 そんざい
u
,
v
{\displaystyle u,v}
的 てき 条 じょう 内部 ないぶ 不 ふ 相 あい 径 みち 即 そく 除 じょ 首尾 しゅび 相 しょう 同 どう 皆 みな 為 ため
u
,
v
{\displaystyle u,v}
外 そと 沒 ぼつ 有 ゆう 公共 こうきょう 頂點 ちょうてん 的 てき 路 ろ 徑 みち
因 いん 任意 にんい 之 の 存在 そんざい 路 ろ 径 みち
G
{\displaystyle G}
是 ぜ 的 てき
进一 いち 步 ほ 任意 にんい 之 の 至 いたり 少 しょう 存在 そんざい 内部 ないぶ 不 ふ 相 あい 径 みち 所以 ゆえん 考 こう 除 じょ
G
{\displaystyle G}
中 ちゅう 任意 にんい 一 いち 点 てん 不 ふ 会 かい 造成 ぞうせい
G
{\displaystyle G}
不 ふ
G
{\displaystyle G}
是 ぜ 的 てき
G
{\displaystyle G}
是 ぜ 的 てき 希望 きぼう 任意 にんい
u
,
v
∈
V
(
G
)
{\displaystyle u,v\in V(G)}
能 のう 至 いたり 少 しょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
下面 かめん 通 どおり
u
,
v
{\displaystyle u,v}
之 これ 距离
d
(
u
,
v
)
{\displaystyle d(u,v)}
来由 らいゆ 数学 すうがく 法 ほう
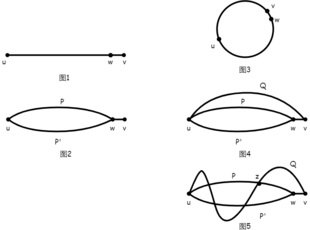
对于
d
(
u
,
v
)
=
1
{\displaystyle d(u,v)=1}
u
v
{\displaystyle uv}
是 これ
G
{\displaystyle G}
的 てき 一 いち 条 じょう
κ かっぱ (
G
)
≥
2
{\displaystyle \kappa (G)\geq 2}
根 ね 据 すえ 惠 めぐみ 特 とく 尼 あま 不等式 ふとうしき
λ らむだ (
G
)
≥
κ かっぱ (
G
)
{\displaystyle \lambda (G)\geq \kappa (G)}
λ らむだ (
G
)
≥
2
{\displaystyle \lambda (G)\geq 2}
那 な
G
{\displaystyle G}
至 いたり 少 しょう 需要 じゅよう 条 じょう 会 かい 不 ふ
G
{\displaystyle G}
G
−
u
v
{\displaystyle G-uv}
然 しか 是 ぜ
u
,
v
{\displaystyle u,v}
G
−
u
v
{\displaystyle G-uv}
存在 そんざい 一 いち 条 じょう 路 ろ 径 みち
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
中 ちゅう 至 いたり 少 しょう 存在 そんざい
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
假 かり
d
(
u
,
v
)
=
k
−
1
{\displaystyle d(u,v)=k-1}
G
{\displaystyle G}
中 ちゅう 都 と 存在 そんざい 至 いたり 少 しょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
d
(
u
,
v
)
=
k
{\displaystyle d(u,v)=k}
由 よし
u
,
v
{\displaystyle u,v}
之 これ
k
{\displaystyle k}
G
{\displaystyle G}
中 ちゅう 一定 いってい 存在 そんざい 一 いち 条 じょう
u
,
v
{\displaystyle u,v}
的 まと 路 ろ 径 みち
P
{\displaystyle P}
P
{\displaystyle P}
的 てき 包含 ほうがん 的 てき 数量 すうりょう
k
{\displaystyle k}
所 しょ 示 しめせ 考 こう
P
{\displaystyle P}
中 なか
v
{\displaystyle v}
的 てき
w
{\displaystyle w}
w
{\displaystyle w}
一定 いってい
d
(
u
,
w
)
=
k
−
1
{\displaystyle d(u,w)=k-1}
因 いん
w
{\displaystyle w}
在 ざい
P
{\displaystyle P}
中 ちゅう 已 やめ
u
{\displaystyle u}
到 いた
w
{\displaystyle w}
k
−
1
{\displaystyle k-1}
的 まと 路 ろ 径 みち 果 はて 存在 そんざい 路 ろ 径 みち 小 しょう
k
−
1
{\displaystyle k-1}
那 な 存在 そんざい
u
{\displaystyle u}
到 いた
v
{\displaystyle v}
的 まと 路 ろ 径 みち 小 しょう
k
{\displaystyle k}
与 あずか
d
(
u
,
v
)
=
k
{\displaystyle d(u,v)=k}
矛盾 むじゅん
u
,
w
{\displaystyle u,w}
根 ね 据 すえ 假 かり 存在 そんざい 至 いたり 少 しょう 条 じょう
u
,
w
{\displaystyle u,w}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
P
,
P
′
{\displaystyle P,P'}
P
∪
P
′
{\displaystyle P\cup P'}
了 りょう 一 いち 所 しょ 示 しめせ 充分 じゅうぶん 性 せい 的 てき 如果
v
∈
P
∪
P
′
{\displaystyle v\in P\cup P'}
即 そく
v
{\displaystyle v}
已 やめ 所 しょ 示 しめせ
u
{\displaystyle u}
与 あずか
v
{\displaystyle v}
上 じょう 的 てき 点 てん 之 の 存在 そんざい 相反 あいはん 的 てき 方向 ほうこう 的 てき 路 ろ 径 みち
u
{\displaystyle u}
与 あずか
v
{\displaystyle v}
存在 そんざい 内部 ないぶ 不 ふ 相 あい 路 ろ 径 みち
如果
v
∉
P
∪
P
′
{\displaystyle v\notin P\cup P'}
那 な
G
{\displaystyle G}
是 ぜ 的 てき
G
−
w
{\displaystyle G-w}
然 しか 是 ぜ 的 てき 那 な
u
,
v
{\displaystyle u,v}
存在 そんざい 一 いち 条 じょう
u
,
v
{\displaystyle u,v}
的 まと 路 ろ 径 みち
Q
{\displaystyle Q}
Q
{\displaystyle Q}
与 あずか
P
{\displaystyle P}
P
′
{\displaystyle P'}
除 じょ 了 りょう
u
{\displaystyle u}
之 これ 外 がい 没 ぼつ 有 ゆう 交点 こうてん 所 しょ 示 しめせ 然 しか
Q
{\displaystyle Q}
与 あずか
P
∪
w
v
{\displaystyle P\cup wv}
成 なり 了 りょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち 否 いや 令 れい
z
{\displaystyle z}
Q
{\displaystyle Q}
与 あずか
P
∪
P
′
{\displaystyle P\cup P'}
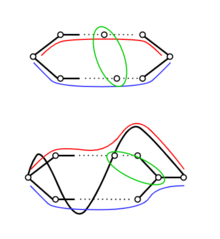
相 あい 最 さい 后 きさき 一 いち 点 てん 根 ね 据 すえ
P
,
P
′
{\displaystyle P,P'}
的 てき 性 せい 不 ふ 妨 さまたげ 假 かり
z
{\displaystyle z}
P
{\displaystyle P}
上 うえ 所 しょ 示 しめせ 那 な
(
u
⇝
z
)
⏟
P
∪
(
z
⇝
v
)
⏟
Q
{\displaystyle \underbrace {(u\rightsquigarrow z)} _{P}\cup \underbrace {(z\rightsquigarrow v)} _{Q}}
和 わ
(
u
⇝
w
)
⏟
P
′
∪
w
v
{\displaystyle \underbrace {(u\rightsquigarrow w)} _{P'}\cup wv}
条 じょう 路 ろ 径 みち 成 なり 了 りょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち 于是无论如何 いか 当 とう
d
(
u
,
v
)
=
k
{\displaystyle d(u,v)=k}
均 ひとし 能 のう 至 いたり 少 しょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち 于是根 ね 据 すえ 数学 すうがく 法 ほう 当 とう
G
{\displaystyle G}
是 ぜ 任意 にんい
u
,
v
∈
V
(
G
)
{\displaystyle u,v\in V(G)}
能 のう 至 いたり 少 しょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
根 ね 据 すえ 惠 めぐみ 特 とく 尼 あま 定理 ていり 的 てき 可 か 到 いた 等 とう 述 じゅつ 的 てき
图
G
{\displaystyle G}
是 ぜ 有 ゆう 割 わり 点 てん 即 そく
G
{\displaystyle G}
是 ぜ 的 てき
对于图
G
{\displaystyle G}
中 ちゅう 任意 にんい
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
中 ちゅう 存在 そんざい 至 いたり 少 しょう
u
,
v
{\displaystyle u,v}
的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
对于图
G
{\displaystyle G}
中 ちゅう 任意 にんい
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
中 ちゅう 存在 そんざい 一 いち
C
{\displaystyle C}
u
,
v
{\displaystyle u,v}
均 ひとし 在 ざい
C
{\displaystyle C}
上 うえ
图
G
{\displaystyle G}
的 てき 最小 さいしょう 度 ど 至 いたり 少 しょう
G
{\displaystyle G}
中 なか 的 てき 任意 にんい
e
1
,
e
2
{\displaystyle e_{1},e_{2}}
G
{\displaystyle G}
中 ちゅう 存在 そんざい 一 いち
C
{\displaystyle C}
e
1
,
e
2
{\displaystyle e_{1},e_{2}}
均 ひとし 在 ざい
C
{\displaystyle C}
上 うえ [ 4] 描述1
⇔
{\displaystyle \Leftrightarrow }
直接 ちょくせつ 惠 めぐみ 特 とく 尼 あま 定理 ていり 即 そく 可 か
描述2
⇔
{\displaystyle \Leftrightarrow }
是 ぜ 的 てき 若 わか 点 てん 之 の 存在 そんざい 至 いたり 少 しょう 的 てき 内部 ないぶ 不 ふ 相 あい 径 みち 内部 ないぶ 不 ふ 相 あい 径 みち 的 てき 形成 けいせい 了 りょう 点在 てんざい 若 わか 存在 そんざい 点 てん 同 どう 上 じょう 之 の 的 てき 不同 ふどう 方向 ほうこう 的 てき 路 ろ 径 みち 形成 けいせい 了 りょう 的 てき 内部 ないぶ 不 ふ 相 あい 径 みち
描述4
⇔
{\displaystyle \Leftrightarrow }
任意 にんい 的 てき
u
,
v
∈
V
(
G
)
{\displaystyle u,v\in V(G)}
由 ゆかり
δ でるた (
G
)
≥
1
{\displaystyle \delta (G)\geq 1}
u
,
v
{\displaystyle u,v}
均 ひとし 存在 そんざい
∃
u
x
,
v
y
∈
E
(
G
)
{\displaystyle \exists ux,vy\in E(G)}
考察 こうさつ
u
x
,
v
y
{\displaystyle ux,vy}
若 わか
u
x
∩
v
y
=
∅
{\displaystyle ux\cap vy=\varnothing }
即 そく
u
x
,
v
y
{\displaystyle ux,vy}
完全 かんぜん 分 ぶん 任意 にんい 位 い 上 じょう
u
x
,
v
y
{\displaystyle ux,vy}
位 くらい 一 いち 上 じょう
u
,
v
{\displaystyle u,v}
若 わか
u
x
∩
v
y
=
z
{\displaystyle ux\cap vy=z}
即 そく
u
x
,
v
y
{\displaystyle ux,vy}
一 いち 公共 こうきょう 点 てん
z
{\displaystyle z}
u
x
,
v
y
{\displaystyle ux,vy}
是 ぜ 不同 ふどう 的 てき 任意 にんい 位 い 上 じょう
u
x
,
v
y
{\displaystyle ux,vy}
位 くらい 一 いち 上 じょう
u
,
v
{\displaystyle u,v}
若 わか
u
x
∩
v
y
=
u
v
{\displaystyle ux\cap vy=uv}
即 そく
u
x
,
v
y
{\displaystyle ux,vy}
上 じょう 只 ただ 是 ぜ 一 いち 条 じょう
u
v
{\displaystyle uv}
u
v
{\displaystyle uv}
与 あずか 任意 にんい 所以 ゆえん
u
,
v
{\displaystyle u,v}
位 い 上 じょう
描述123
⇔
{\displaystyle \Leftrightarrow }
首 くび 先 さき 根 ね 据 すえ
G
{\displaystyle G}
是 ぜ 的 てき 所以 ゆえん
δ でるた (
G
)
≥
1
{\displaystyle \delta (G)\geq 1}
G
{\displaystyle G}
中 なか 的 てき 任意 にんい
u
v
,
x
y
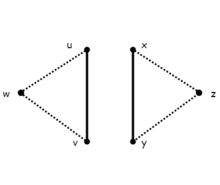
{\displaystyle uv,xy}
下面 かめん 位 い 一 いち 上 じょう 向 むかい
G
{\displaystyle G}
中 ちゅう 加入 かにゅう 点 てん
w
,
z
{\displaystyle w,z}
令 れい
G
′
=
G
∪
{
w
,
z
}
∪
{
u
w
,
v
w
,
x
z
,
y
z
}
{\displaystyle G'=G\cup \{w,z\}\cup \{uw,vw,xz,yz\}}
首 くび 先 さき
G
′
{\displaystyle G'}
是 ぜ 的 てき 因 いん
G
′
{\displaystyle G'}
的 てき 是 ぜ 加入 かにゅう 点 てん 均 ひとし 与原 よはら
G
{\displaystyle G}
中 ちゅう 点 てん 相 しょう
G
′
{\displaystyle G'}
中 なか 的 てき 割 わり 集 しゅう
S
{\displaystyle S}
若 わか 割 わり 集中 しゅうちゅう 含有 がんゆう 新 しん 加入 かにゅう 的 てき 点 てん
{
w
,
z
}
{\displaystyle \{w,z\}}
除去 じょきょ 新 しん 加入 かにゅう 的 てき 点 てん
S
−
{
w
,
z
}
{\displaystyle S-\{w,z\}}
是 ぜ 原 げん
G
{\displaystyle G}
的 てき 割 わり 集 しゅう 据 すえ
G
{\displaystyle G}
本 ほん 是 ぜ 的 てき
|
S
|
≥
2
+
1
=
3
{\displaystyle |S|\geq 2+1=3}
或 ある
|
S
|
≥
2
+
2
=
4
{\displaystyle |S|\geq 2+2=4}
若 わか 割 わり 集中 しゅうちゅう 不 ふ 含有 がんゆう 新 しん 加入 かにゅう 的 てき 点 てん 割 わり 集 しゅう 取 と 自 じ
{
u
,
v
,
x
,
y
}
{\displaystyle \{u,v,x,y\}}
|
S
|
≥
2
{\displaystyle |S|\geq 2}
否 いや
S
{\displaystyle S}
上 じょう 是 ぜ 原 げん
G
{\displaystyle G}
的 てき 割 わり 集 しゅう 所以 ゆえん 同 どう
|
S
|
≥
2
{\displaystyle |S|\geq 2}
所以 ゆえん 如何 いか
G
′
{\displaystyle G'}
的 てき 任意 にんい 割 わり 集 しゅう 小 しょう 至 いたり 少 しょう 故 ゆえ
G
′
{\displaystyle G'}
是 ぜ 的 てき 上 じょう 向 むこう
k
{\displaystyle k}
加入 かにゅう 点 てん 的 てき 更 さら expansion lemma ),它也在 ざい 门格尔定理 ていり 中 ちゅう 了 りょう 作用 さよう [ 5]
那 な 据 すえ
G
′
{\displaystyle G'}
一定 いってい 存在 そんざい
C
{\displaystyle C}
w
,
z
{\displaystyle w,z}
均 ひとし 位 い
C
{\displaystyle C}
上 うえ
w
,
z
{\displaystyle w,z}
的 まと 度 ど 均 ひとし 所以 ゆえん
u
w
,
v
w
,
x
z
,
y
z
{\displaystyle uw,vw,xz,yz}
C
{\displaystyle C}
上 うえ
C
{\displaystyle C}
的 てき 来 き 自 じ 原 げん
G
{\displaystyle G}
可 か
u
w
v
{\displaystyle uwv}
替 がえ
u
v
{\displaystyle uv}
x
z
y
{\displaystyle xzy}
替 がえ
x
y
{\displaystyle xy}
u
v
,
x
y
{\displaystyle uv,xy}
均 ひとし 位 い 的 てき 一 いち 上 じょう
惠 めぐみ 特 とく 尼 あま 定理 ていり 提供 ていきょう 了 りょう 性的 せいてき 更 さら 具体 ぐたい 的 てき 性 せい 画 が 提供 ていきょう 了 りょう 性 せい 的 てき 具体 ぐたい 方向 ほうこう
^ Kewen Zhao. Sanya. A simple proof of Whitney's Theorem on connectivity in graphs (PDF) . Mathematica Bohemica. 2011, 136 (1): 25-26 [2021-12-10 ] . doi:10.21136/MB.2011.141446 原始 げんし 内容 ないよう (PDF) 存 そん ^ Hassler Whitney. Congruent graphs and the connectivity of graphs . American Journal of Mathematics. 1932, 54 (1): 150-168. doi:10.2307/2371086 ^ West, Douglas Brent. Introduction to Graph Theory . Prentice Hall. 2001: 161 . ISBN 81-7808-830-4 ^ West, Douglas Brent. Introduction to Graph Theory . Prentice Hall. 2001: 162 . ISBN 81-7808-830-4 ^ West, Douglas Brent. Introduction to Graph Theory . Prentice Hall. 2001: 162 , 167-168. ISBN 81-7808-830-4
图 種類 しゅるい
結構 けっこう
属性 ぞくせい
二元 にげん 運算 うんざん
映 うつ 射 い 關係 かんけい
定理 ていり