a の平方根 へいほうこん 英 えい square root )とは、数 かず 対 たい 平方 へいほう a になる数 かず
複素数 ふくそすう 平方根 へいほうこん 代数 だいすう 学 がく 基本 きほん 定理 ていり 0 を除 のぞ 個 こ 存在 そんざい
特 とく 実数 じっすう 範囲 はんい 正 せい 実数 じっすう 平方根 へいほうこん 互 たが 反 はん 数 かず 個 こ 実数 じっすう 幾何 きか 学 がく 的 まと 正 せい 実数 じっすう 対 たい 正 せい 平方根 へいほうこん 与 あた 正方形 せいほうけい 面積 めんせき 対 たい 一 いち 辺 へん 長 なが
二乗根 じじょうこん 自乗根 じじょうこん 呼 よ
0 の平方根 へいほうこん 0 のみであり、平方根 へいほうこん 一意 いちい 定 さだ 限 かぎ
任意 にんい a に対 たい a の正 せい 平方根 へいほうこん 長 なが 単位 たんい 長 ちょう 与 あた 定規 じょうぎ 作図 さくず
数 かず a に対 たい x 2 = a 満 み x を a の平方根 へいほうこん 元 もと 数 かず a がどのような数 かず 範囲 はんい 概念 がいねん 意味 いみ 持 も 含 ふく 点 てん 差異 さい 生 しょう 注意 ちゅうい 必要 ひつよう
0 平方根 へいほうこん 0 のみである。元 もと 数 かず a が正 せい 数 かず 場合 ばあい 平方根 へいほうこん 正 せい 負 まけ 存在 そんざい 絶対 ぜったい 値 ち 等 ひと 正 せい 方 ほう 根号 こんごう
{\displaystyle {\sqrt {\;}}}
用 もち
a
{\displaystyle {\sqrt {a}}}
と表 あらわ a の「正 せい 非負 ひふ 平方根 へいほうこん principal square root ; 主 しゅ 平方根 へいほうこん 文脈 ぶんみゃく 上 じょう 紛 まぎ 無 な 思 おも 正 せい 省略 しょうりゃく 他方 たほう 負 まけ 平方根 へいほうこん
−
a
{\displaystyle -{\sqrt {a}}}
平方根 へいほうこん 併 あわ
±
a
{\displaystyle \pm {\sqrt {a}}}
表記 ひょうき 例 たと 9 の平方根 へいほうこん ±3 、すなわち +3 と −3 の2つであり、
9
{\displaystyle {\sqrt {9}}}
正 せい 3 の方 ほう 表 あらわ
0
{\displaystyle {\sqrt {0}}}
0 の唯一 ゆいいつ 平方根 へいほうこん 0 を意味 いみ 約束 やくそく
a <0a の平方根 へいほうこん 実数 じっすう 平方根 へいほうこん 数 かず 大小 だいしょう 区別 くべつ
また、数 かず 限 かぎ 一般 いっぱん 数学 すうがく 的 てき 対象 たいしょう 意味 いみ 仕方 しかた 平方根 へいほうこん 定義 ていぎ 正 せい 定値 ていち 行列 ぎょうれつ
基本 きほん 的 てき 性質 せいしつ [ 編集 へんしゅう ] 実数 じっすう 平方根 へいほうこん [ 編集 へんしゅう ] a が正 せい 整数 せいすう a の平方根 へいほうこん 整数 せいすう 限 かぎ
元 もと 数 かず 平方 へいほう 数 すう 正 せい 整数 せいすう 平方根 へいほうこん 無理 むり 数 すう 証明 しょうめい
(例 れい
10
=
3.162277660168
⋯
{\displaystyle {\sqrt {10}}=3.162277660168\cdots }
a > 0, b > 0
a
2
b
=
a
b
{\displaystyle {\sqrt {a^{2}b}}=a{\sqrt {b}}}
が成 な 立 た 例 たと
8
=
2
2
×
2
=
2
2
{\displaystyle {\sqrt {8}}={\sqrt {2^{2}\times 2}}=2{\sqrt {2}}}
12
=
2
2
×
3
=
2
3
{\displaystyle {\sqrt {12}}={\sqrt {2^{2}\times 3}}=2{\sqrt {3}}}
54
=
3
2
×
6
=
3
6
{\displaystyle {\sqrt {54}}={\sqrt {3^{2}\times 6}}=3{\sqrt {6}}}
… である。
したがって特 とく 正 せい 整数 せいすう x が平方 へいほう 因子 いんし 持 も
x
{\displaystyle {\sqrt {x}}}
無理 むり 数 すう
概数 がいすう 求 もと 方 かた [ 編集 へんしゅう ] 有理数 ゆうりすう 平方 へいほう 正 せい 実数 じっすう 平方根 へいほうこん 小数 しょうすう 部分 ぶぶん 循環 じゅんかん 小数 しょうすう 表示 ひょうじ 効率 こうりつ 的 てき 求 もと 方法 ほうほう 開平 かいへい 法 ほう 知 し
比較的 ひかくてき 小 ちい 数 かず 平方根 へいほうこん 概数 がいすう 知 し 必要 ひつよう 以下 いか 小数 しょうすう 部分 ぶぶん 数 すう 桁 けた 目 め 語呂合 ごろあ 知 し
2
=
1.41421356
⋯
{\displaystyle {\sqrt {2}}=1.41421356\cdots }
一夜 いちや 一 いち 夜 や 人見 ひとみ 頃 ごろ
3
=
1.7320508075
⋯
{\displaystyle {\sqrt {3}}=1.7320508075\cdots }
人並 ひとな 奢 おご 女子 じょし
5
=
2.2360679
⋯
{\displaystyle {\sqrt {5}}=2.2360679\cdots }
富士山 ふじさん 麓 ふもと 鸚鵡 おうむ 鳴 な 「富士 ふじ 山麓 さんろく に 鸚鵡 おうむ 鳴 な 誤 あやま 覚 おぼ 向 む 多 おお
5
=
2.236067977
⋯
{\displaystyle {\sqrt {5}}=2.236067977\cdots }
小数点 しょうすうてん 以下 いか 桁 けた 切 き 捨 す 四捨五入 ししゃごにゅう 方 ほう 近 ちか
6
=
2.4494897
⋯
{\displaystyle {\sqrt {6}}=2.4494897\cdots }
串 くし 焼 や 煮 に 良 よ 弱 よわ 000 ≈ 2.44949 似 に 良 よ 良 よ 二 に 夜 や
7
=
2.64575
⋯
{\displaystyle {\sqrt {7}}=2.64575\cdots }
菜 さい 虫 むし 来 こ 菜 さい 虫 むし
8
=
2
2
=
2.828427
⋯
{\displaystyle {\sqrt {8}}=2{\sqrt {2}}=2.828427\cdots }
呼 よ
10
=
3.162277
⋯
{\displaystyle {\sqrt {10}}=3.162277\cdots }
父 ちち 一 いち 郎 ろう 兄 にい 任意 にんい 実数 じっすう x 対 たい
x
2
=
|
x
|
(
=
{
x
(
x
≥
0
)
−
x
(
x
<
0
)
)
{\displaystyle {\sqrt {x^{2}}}=|x|\left(={\begin{cases}x&(x\geq 0)\\-x&(x<0)\end{cases}}\right)}
が成 な 立 た
積 せき 商 しょう 関 かん 計算 けいさん 法則 ほうそく [ 編集 へんしゅう ] a >0b >0
a
b
=
a
b
,
a
b
=
a
b
{\displaystyle {\begin{aligned}{\sqrt {ab}}&={\sqrt {a}}{\sqrt {b}},\\{\sqrt {\frac {a}{b}}}&={\frac {\sqrt {a}}{\sqrt {b}}}\end{aligned}}}
が成 な 立 た [1]
累乗 るいじょう 根 ね 表記 ひょうき [ 編集 へんしゅう ] x ≥ 0対 たい 冪 べき 乗 じょう 冪 べき 根 ね
x
=
(
x
)
2
=
(
x
2
4
)
2
=
(
x
3
6
)
2
=
⋯
{\displaystyle x=\left({\sqrt {x}}\right)^{2}=\left({\sqrt[{4}]{x^{2}}}\right)^{2}=\left({\sqrt[{6}]{x^{3}}}\right)^{2}=\cdots }
が成 な 立 た 特 とく
x
1
/
2
:=
x
{\displaystyle x^{1/2}:={\sqrt {x}}}
と定 さだ 指数 しすう 表示 ひょうじ 1 / 2 2 / 4 3 / 6 依 よ 一定 いってい 意味 いみ well-defined で、指数 しすう 法則 ほうそく 整合 せいごう
平方根 へいほうこん 関数 かんすう [ 編集 へんしゅう ] 入力 にゅうりょく x に対 たい 非負 ひふ 平方根 へいほうこん
x
{\displaystyle {\sqrt {x}}}
返 かえ 函数 かんすう
f
(
x
)
=
x
{\displaystyle f(x)={\sqrt {x}}}
非負 ひふ 実数 じっすう 全体 ぜんたい 集合 しゅうごう R + ∪ {0}上 うえ 定義 ていぎ 考 かんが 正 せい 平方根 へいほうこん 函数 かんすう
∙
:
R
+
∪
{
0
}
∋
x
→
1-1,onto
x
∈
R
+
∪
{
0
}
{\displaystyle {\sqrt {\bullet }}\colon \mathbb {R} ^{+}\cup \{0\}\ni x\ {\xrightarrow {\text{1-1,onto}}}\ {\sqrt {x}}\in \mathbb {R} ^{+}\cup \{0\}}
は(函数 かんすう well-defined で)、それ自身 じしん 全 ぜん 単 たん 射 しゃ 正 せい 平方根 へいほうこん 函数 かんすう グラフ と負 まけ 平方根 へいほうこん 函数 かんすう
−
∙
:
R
+
∪
{
0
}
∋
x
→
1-1,onto
−
x
∈
R
−
∪
{
0
}
{\displaystyle {-{\sqrt {\bullet }}}\colon \mathbb {R} ^{+}\cup \{0\}\ni x\ {\xrightarrow {\text{1-1,onto}}}\ {-{\sqrt {x}}}\in \mathbb {R} ^{-}\cup \{0\}}
のグラフの和 わ 集合 しゅうごう 二 に 次 じ 函数 かんすう y = x 2 直線 ちょくせん y = x 関 かん 線 せん 対称 たいしょう 放物線 ほうぶつせん 等 ひと
正 せい 平方根 へいほうこん 函数 かんすう 放物線 ほうぶつせん 半分 はんぶん 正 せい 平方根 へいほうこん 函数 かんすう 連続 れんぞく x > 0微分 びぶん 可能 かのう 導 しるべ 関数 かんすう
d
d
x
x
=
1
2
x
{\displaystyle {\frac {d}{dx}}{\sqrt {x}}={\frac {1}{2{\sqrt {x}}}}}
不定 ふてい 積分 せきぶん
∫
x
d
x
=
2
3
(
x
)
3
+
C
=
2
3
x
3
2
+
C
{\displaystyle \int {\sqrt {x}}\,dx={\frac {2}{3}}({\sqrt {x}})^{3}+C={\frac {2}{3}}x^{\frac {3}{2}}+C}
C 積分 せきぶん 定数 ていすう で与 あた 収束 しゅうそく 冪 べき 級数 きゅうすう 二 に 項 こう 展開 てんかい
1
+
x
=
∑
n
=
0
∞
(
1
/
2
n
)
x
n
=
1
+
x
2
−
x
2
8
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
(
1
−
2
n
)
(
n
!
)
2
(
4
n
)
x
n
{\displaystyle {\sqrt {1+x}}=\sum _{n=0}^{\infty }{\binom {1/2}{n}}x^{n}=1+{\frac {x}{2}}-{\frac {x^{2}}{8}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}}
が |x | < 1 で成 な 立 た
x > 0自然 しぜん 数 すう n に対 たい 帰納的 きのうてき
f
n
(
x
)
=
x
+
x
+
x
+
x
+
.
.
.
{\displaystyle f_{n}(x)={\sqrt {x+{\sqrt {x+{\sqrt {x+{\sqrt {x+...}}}}}}}}}
(x および根号 こんごう 個数 こすう n )と定 さだ 函 はこ 数列 すうれつ (fn ) は漸 やや 化 か 式 しき
f
n
+
1
(
x
)
2
=
x
+
f
n
(
x
)
{\displaystyle f_{n+1}(x)^{2}=x+f_{n}(x)}
に従 したが (fn ) は α あるふぁ x ) > 0収束 しゅうそく α あるふぁ x )2 − α あるふぁ x ) − x = 0
lim
n
→
∞
f
n
(
x
)
=
x
+
1
4
+
1
2
{\displaystyle \lim _{n\to \infty }f_{n}(x)={\sqrt {x+{\frac {1}{4}}}}+{\frac {1}{2}}}
が成 な 立 た
負 まけ 数 かず 平方根 へいほうこん [ 編集 へんしゅう ] 負 まけ 数 かず 平方根 へいほうこん 実数 じっすう 虚数 きょすう 虚数 きょすう 単位 たんい i (i 2 = −1)用 もち 表 あらわ a > 0−a の平方根 へいほうこん
a
A
i
{\displaystyle {\sqrt {a{\vphantom {A}}}}i}
−
a
A
i
{\displaystyle -{\sqrt {a{\vphantom {A}}}}i}
x 2 = −a 解 かい
x
=
±
a
A
i
{\displaystyle x=\pm {\sqrt {a{\vphantom {A}}}}i}
[2] a > 0
−
a
A
{\displaystyle {\sqrt {-a{\vphantom {A}}}}}
−
a
A
=
a
A
i
{\displaystyle {\sqrt {-a{\vphantom {A}}}}={\sqrt {a{\vphantom {A}}}}i}
で定義 ていぎ 例 たと −3 の平方根 へいほうこん
3
i
{\displaystyle {\sqrt {3}}i}
−
3
i
{\displaystyle -{\sqrt {3}}i}
x 2 = −3解 かい
±
3
i
{\displaystyle \pm {\sqrt {3}}i}
[2]
−
3
=
3
i
{\displaystyle {\sqrt {-3}}={\sqrt {3}}i}
有理数 ゆうりすう 体 からだ Q 有理数 ゆうりすう 全体 ぜんたい 負 まけ 数 かず 含 ふく 上 じょう 定義 ていぎ 函数 かんすう
Q
∋
x
↦
x
∈
A
{\displaystyle \mathbb {Q} \ni x\mapsto {\sqrt {x}}\in \mathbb {A} }
において、その値域 ちいき 虚数 きょすう 含 ふく 代数 だいすう 的 てき 数 すう 一部 いちぶ 有理数 ゆうりすう 平方根 へいほうこん 再 ふたた 有理数 ゆうりすう 有理数 ゆうりすう 有理数 ゆうりすう 範囲 はんい 平方 へいほう 数 すう 有理数 ゆうりすう 内 ない 平方 へいほう 数 すう 有理数 ゆうりすう d に対 たい √ d 二 に 次 じ 無理 むり 数 すう Q √ d 付 つ 加 くわ 得 え 体 からだ 二 に 次 じ 体 たい 総称 そうしょう
複素数 ふくそすう 平方根 へいほうこん [ 編集 へんしゅう ] a が 0 でない複素数 ふくそすう z 2 = a 満 み 複素数 ふくそすう z は2個 こ 存在 そんざい a の極 ごく 形式 けいしき
a
=
r
e
i
θ しーた
(
r
>
0
,
−
π ぱい <
θ しーた ≤
π ぱい )
{\displaystyle a=re^{i\theta }\ (r>0,\,-\pi <\theta \leq \pi )}
とすると、z の動 どう 径 みち 乗 じょう r 、z の偏 へん 角 かく 倍 ばい θ しーた
a
=
r
e
i
θ しーた
/
2
{\displaystyle {\sqrt {a}}={\sqrt {r}}\,e^{i\theta /2}}
と定義 ていぎ a に対 たい 一意 いちい 定 さだ (√ a 2 = a を満 み a の平方根 へいほうこん 主 おも 値 ち 主 おも 値 ち 定義 ていぎ 平方根 へいほうこん 函数 かんすう
C
∋
z
↦
z
∈
C
{\displaystyle \mathbb {C} \ni z\mapsto {\sqrt {z}}\in \mathbb {C} }
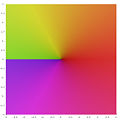
は、実 じつ 軸 じく 負 まけ 部分 ぶぶん 除 のぞ ガウス平面 へいめん C 全域 ぜんいき 至 いた 所 ところ 正則 せいそく 実 じつ 軸 じく 負 まけ 部分 ぶぶん 上 じょう 連続 れんぞく 枚 まい 平面 へいめん 実 じつ 軸 じく 負 まけ 部分 ぶぶん 張 は 合 あ 平方根 へいほうこん 函数 かんすう リーマン面 めん 上 うえ 考 かんが 至 いた 所 ところ 解析 かいせき 的 てき
ガウス平面 へいめん 上 じょう 平方根 へいほうこん 函数 かんすう 色 いろ 示 しめ 原点 げんてん 周 まわ 偏 へん 角 かく 正 せい 方向 ほうこう 反 はん 時計 とけい 回 まわ 回 まわ 実 じつ 軸 じく 負 まけ 部分 ぶぶん 跨 また 一 いち 枚 まい 平面 へいめん 跳 と 緑 みどり 緑 みどり
もう一 いち 枚 まい 平面 へいめん 上 じょう 平方根 へいほうこん 函数 かんすう 原点 げんてん 正 せい 方向 ほうこう 回 まわ 実 じつ 軸 じく 負 まけ 部分 ぶぶん 境 さかい 最初 さいしょ 平面 へいめん 帰 かえ 紫 むらさき 紫 むらさき
原点 げんてん 付近 ふきん 平方根 へいほうこん 函数 かんすう 面 めん 平面 へいめん 張 は 合 あ 様子 ようす 平方根 へいほうこん 関数 かんすう z 1/2 z は複素数 ふくそすう
数 すう 以外 いがい 平方根 へいほうこん [ 編集 へんしゅう ] 行列 ぎょうれつ 平方根 へいほうこん [ 編集 へんしゅう ] 一般 いっぱん 正方 まさかた 行列 ぎょうれつ A に対 たい X2 =A を満 み 正方 せいほう 行列 ぎょうれつ X を A の平方根 へいほうこん 行列 ぎょうれつ 呼 よ [3] 記号 きごう √ A A 1 ⁄2 表 あらわ 平方根 へいほうこん 行列 ぎょうれつ 存在 そんざい 限 かぎ 存在 そんざい 場合 ばあい 複数個 ふくすうこ 場合 ばあい 無限 むげん 個 こ 存在 そんざい 場合 ばあい 例 たと 二 に 次 じ 単位 たんい 行列 ぎょうれつ I 2 無数 むすう 平方根 へいほうこん 持 も [4] 中 なか 正 せい 定値 ていち 一 ひと I 2 自身 じしん
また、半 はん 正 せい 定値 ていち 複素 ふくそ 実 み 正方 まさかた 行列 ぎょうれつ A に対 たい A = BB *A = B *B .∗ はエルミート共軛 きょうやく )を満 み 正方 せいほう 限 かぎ 任意 にんい 行列 ぎょうれつ B をしばしば、 A の非 ひ 非対称 ひたいしょう 平方根 へいほうこん non-Hermitian (resp. symmetric) square root )[5] 呼 よ 適当 てきとう 三角 さんかく 行列 ぎょうれつ 因子 いんし [6] 呼 よ B がそれ自身 じしん 実 じつ 係数 けいすう 場合 ばあい 対称 たいしょう 上 うえ 述 の 平方根 へいほうこん 概念 がいねん 一致 いっち 任意 にんい 正 せい 定値 ていち 行列 ぎょうれつ P に対 たい 自身 じしん 正 せい 定値 ていち 平方根 へいほうこん 一意 いちい 主 しゅ 平方根 へいほうこん [7] 呼 よ 記号 きごう √ P P 1/2 専 もっぱ 主 しゅ 平方根 へいほうこん 表 あらわ 予約 よやく [8] 注意 ちゅうい 正 せい 定値 ていち 行列 ぎょうれつ 任意 にんい 非 ひ 平方根 へいほうこん ユニタリ行列 ぎょうれつ を掛 か 分 ぶん 不定 ふてい 性 せい 持 も [9] 正 せい 実数 じっすう 場合 ばあい 正 せい 値 ち 主 しゅ 平方根 へいほうこん 一意 いちい 決 き 主 しゅ 平方根 へいほうこん ±1 を掛 か 平方根 へいほうこん 対応 たいおう
このような半 はん 正 せい 定値 ていち 行列 ぎょうれつ 平方根 へいほうこん 計算 けいさん 一意 いちい 性 せい 証明 しょうめい 作用素 さようそ 関 かん スペクトル論 ろん (固有値 こゆうち 分解 ぶんかい 特異 とくい 値 ち 分解 ぶんかい コレスキー分解 ぶんかい などが利用 りよう [10] [11] [12]
可 か 換 かわ 整 せい 域 いき 可 か 換 かわ 体 からだ 場合 ばあい [ 編集 へんしゅう ] (可 か 換 かわ 整 せい 域 いき 各 かく 元 もと 二 ふた 多 おお 平方根 へいほうこん 持 も 実際 じっさい 乗法 じょうほう 可 か 換 かわ 性 せい 二 に 平方 へいほう 数 すう 差 さ 公式 こうしき (英語 えいご 版 ばん u 2 − v 2 = (u − v )(u + v )成 な 立 た 注意 ちゅうい u, v が同 おな 元 もと 平方根 へいほうこん u 2 − v 2 = 0零 れい 因子 いんし 持 も u = v u + v = 0従 したが 後者 こうしゃ 二 ふた 平方根 へいほうこん 互 たが 加法 かほう 逆 ぎゃく 元 もと 関係 かんけい 言 い 一 ひと 元 もと 平方根 へいほうこん 存在 そんざい 符号 ふごう 違 ちが 除 のぞ 一意 いちい 特 とく 整 せい 域 いき 零 れい 元 げん 0 の平方根 へいほうこん 0 自身 じしん
標 しるべ 数 すう 2 の可 か 換 かわ 体 からだ 各 かく 元 もと 平方根 へいほうこん 一 ひと 持 も 各 かく 元 もと 自身 じしん 加法 かほう 逆 ぎゃく 元 もと 注意 ちゅうい 全 まった 持 も 何 いず 標 しるべ 数 すう 2 の有限 ゆうげん 体 たい 任意 にんい 元 もと 一意 いちい 平方根 へいほうこん 持 も 以外 いがい 任意 にんい 標 しるべ 数 すう 体 からだ 先 さき 段落 だんらく 任意 にんい 非 ひ 零 れい 元 げん 二 ふた 平方根 へいほうこん 持 も 全 まった 持 も 何 いず
奇 き 素数 そすう p と適当 てきとう 正 せい 整数 せいすう e に対 たい q = p e 置 お q -元 もと 体 からだ F q 非 ひ 零 れい 元 げん 平方 へいほう 剰余 じょうよ 平方根 へいほうこん F q 属 ぞく 言 い 平方 へいほう 非 ひ 剰余 じょうよ 体 からだ (q − 1)/2 個 こ 元 もと 平方 へいほう 剰余 じょうよ (q − 1)/2 個 こ 非 ひ 剰余 じょうよ 零 れい 元 げん 属 ぞく 注意 ちゅうい 平方 へいほう 剰余 じょうよ 元 もと 全体 ぜんたい 乗法 じょうほう 関 かん 群 ぐん 成 な 性質 せいしつ 代数 だいすう 的 てき 整数 せいすう 論 ろん 広 ひろ 用 もち
非 ひ 可 か 換 かわ 零 れい 因子 いんし 持 も 環 たまき 場合 ばあい [ 編集 へんしゅう ] 一般 いっぱん 環 たまき a の平方根 へいほうこん b を b 2 = a 定 さだ 一般 いっぱん 平方根 へいほうこん 符号 ふごう 除 のぞ 一意 いちい 限 かぎ
たとえば合同 ごうどう 類 るい 環 たまき Z /8Z 考 かんが 環 たまき 単位 たんい 元 もと 1 は相 あい 異 こと 四 よっ 平方根 へいほうこん 持 も 具体 ぐたい 的 てき ±1, ±3 )。他方 たほう 元 もと 2 は平方根 へいほうこん 持 も 詳細 しょうさい 平方 へいほう 剰余 じょうよ 項 こう 参照 さんしょう
他 た 例 れい 四 よん 元 げん 数 すう 体 からだ H −1 は ±i , ±j , ±k を含 ふく 無数 むすう 平方根 へいほうこん 持 も 実 じつ −1 の平方根 へいほうこん 全体 ぜんたい 集合 しゅうごう
{
a
i
+
b
j
+
c
k
∣
a
2
+
b
2
+
c
2
=
1
}
{\displaystyle \{ai+bj+ck\mid a^{2}+b^{2}+c^{2}=1\}}
であり、したがって各 かく 平方根 へいほうこん 絶対 ぜったい 値 ち 等 ひと 集合 しゅうごう 三 さん 次元 じげん 空間 くうかん 内 ない 二 に 次元 じげん 単位 たんい 球面 きゅうめん 描 えが 四 よん 元 げん 数 すう 平方根 へいほうこん 参照 さんしょう
零 れい 元 げん 0 の平方根 へいほうこん 定義 ていぎ 0 自身 じしん 零 れい 因子 いんし 四 よん 元 げん 数 すう 体 たい 可 か 除 じょ 環 たまき 零 れい 因子 いんし 存在 そんざい 一般 いっぱん 0 の平方根 へいほうこん 0 のみである。しかし、零 れい 因子 いんし 存在 そんざい 一般 いっぱん 環 たまき 必 かなら 反例 はんれい 任意 にんい 自然 しぜん 数 すう n に対 たい Z /n 2 Z 考 かんが 場合 ばあい n は零 れい 因子 いんし 実際 じっさい n 2 = 0満 み
^ “NHK高校 こうこう 講座 こうざ 数学 すうがく 第 だい 章 しょう 指数 しすう 関数 かんすう 対数 たいすう 関数 かんすう 指数 しすう 関数 かんすう 累乗 るいじょう 根 ね 累乗 るいじょう 根 ね 性質 せいしつ ”. 2019年 ねん 月 がつ 日 にち 閲覧 えつらん ^ a b “NHK高校 こうこう 講座 こうざ 数学 すうがく 第 だい 章 しょう 方程式 ほうていしき 式 しき 証明 しょうめい 次 じ 方程式 ほうていしき 複素数 ふくそすう 負 まけ 数 かず 平方根 へいほうこん ”. 2019年 ねん 月 がつ 日 にち 閲覧 えつらん
^ Higham, Nicholas J. (April 1986). “Newton's Method for the Matrix Square Root” . en:Mathematics of Computation 46 (174): 537–549. doi :10.2307/2007992 . http://www.ams.org/journals/mcom/1986-46-174/S0025-5718-1986-0829624-5/S0025-5718-1986-0829624-5.pdf . ^ Mitchell, Douglas W., "Using Pythagorean triples to generate square roots of I2 ", Mathematical Gazette 87, November 2003, 499–500.
^ Marshall, Albert W.; Olkin, Ingram; Arnold, Barry, Inequalities , https://books.google.com/books?id=I9wfajyOrooC&pg=PA773&dq=%22asymmetric%2Bsquare%2Broot%22 ^ Gentle, James E., Matrix Algebra , https://books.google.com/books?id=PDjIV0iWa2cC&pg=PA194&dq=%22Cholesky+factor%22 ^ Higham, Nicholas J., Functions of Matrices , https://books.google.com/books?id=2Wz_zVUEwPkC&pg=PA20&dq=%22unique%2Bsquare%2Broot%22 ^ Gentle, James E., Matrix Algebra , https://books.google.com/books?id=PDjIV0iWa2cC&pg=PA125&dq=%22Cholesky+factor%22 ^ Lu, Andreas, Practical Optimization , https://books.google.com/books?id=6_2RhaMFPLcC&pg=PA601&dq=%22non-hermitian%2Bsquare%2Broot%22 ^ Higham, Nicholas J., Functions of Matrices , https://books.google.com/books?id=2Wz_zVUEwPkC&pg=PA20&dq=%22spectral%2Bdecomposition%22 ^ Gentle, James E., Matrix Algebra , https://books.google.com/books?id=PDjIV0iWa2cC&pg=PA193&dq=%22nonnegative%2Bdefinite%22 ^ Lange, Kenneth, Numerical Analysis for Statisticians , https://books.google.com/books?id=va4_AAAAQBAJ&pg=PA99&dq=%22unique%22
























![{\displaystyle x=\left({\sqrt {x}}\right)^{2}=\left({\sqrt[{4}]{x^{2}}}\right)^{2}=\left({\sqrt[{6}]{x^{3}}}\right)^{2}=\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d812b8d0d5f69eed9cc0db560c3a578f6f587a)