在数学上,每个闭曲面在几何拓扑的意义下,可以由一个偶数条边的有向多边形,把它的边成对地粘合构造出来,这样的多边形称之为基本多边形(fundamental polygon)。
 由一对向量定义的基本平行四边形,生成环面。
由一对向量定义的基本平行四边形,生成环面。
这个构造可以表示成一个长为2n的字符串,一共n个不同的符号,每个符号出现两次带有指数 +1或 -1。指数 -1的符号对应于该边的定向与基本多边形的定向相反。
例子[编辑]
曲面的基本多边形
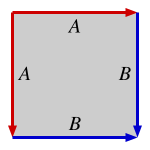
球面
|

实球射影平面
|

克莱因瓶
|
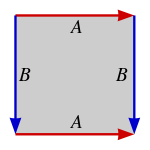
环面
|
上图中标有相同字母的两条边,沿着箭头方向粘合。
- 球面:
 或
或
- 实射影平面:
 或
或
- 克莱因瓶:
 或
或
- 环面:
 或
或
群生成元[编辑]
对标准对称形状,多边形的边可以理解为一个群的生成元。然后这个多边形,写成群元素形式,成为由这些边生成的自由群上一个约束,给出有一个约束的群呈示。
因此,例如给定欧几里得平面 ,设群元素
,设群元素 在这个平面上有作用
在这个平面上有作用 而
而 。则
。则 生成格
生成格 ,而环面由商空间给出(一个齐性空间)
,而环面由商空间给出(一个齐性空间) 。更一般地,两个生成元
。更一般地,两个生成元 可用来生成一个基本平行四边形的平行四边形镶嵌。
可用来生成一个基本平行四边形的平行四边形镶嵌。
对环面,在两个字母的自由群上的约束由 给出。这个约束平凡地包含在如上给出的平面上的作用中。另外,平面可用六边形铺满,六边形的中心形成一个六边形格。将六边形的相对等同,又得到了环面。这一回约束是
给出。这个约束平凡地包含在如上给出的平面上的作用中。另外,平面可用六边形铺满,六边形的中心形成一个六边形格。将六边形的相对等同,又得到了环面。这一回约束是 ,刻划了六边形格生成元在平面上的作用。
,刻划了六边形格生成元在平面上的作用。
在实际中,大部分有趣的情形是具有负曲率的曲面,由群 中一个离散格作用在上半平面实现。这样的格称为富克斯群(Fuchsian group)。
中一个离散格作用在上半平面实现。这样的格称为富克斯群(Fuchsian group)。
标准基本多边形[编辑]
亏格n可定向闭曲面有如下标准基本多边形:

(不可定向)亏格n的不可定向闭曲面有如下标准基本多边形:

或者,不可定向曲面能由两种形式给出,亏格n 克莱因瓶与亏格n 实射影平面。亏格2n克莱因瓶由一个4n边形给出

(注意最后的 没有上标 -1;与可定向情形比较,这个翻转是不可定向性的缘故)。亏格2n+1射影平面由一个4n+2边形给出
没有上标 -1;与可定向情形比较,这个翻转是不可定向性的缘故)。亏格2n+1射影平面由一个4n+2边形给出

最后两类情形穷尽了所有可能的不可定向曲面,这是昂利·庞加莱证明的。
紧黎曼曲面的基本多边形[编辑]
一个(双曲)紧黎曼曲面的基本多边形有许多重要的性质,将曲面与它的富克斯模型(Fuchsian model)联系起来。即一个双曲紧黎曼曲面可以上半平面做为万有覆叠,从而可以表示为一个商流形H/Γ,这里 Γ是一个非阿贝尔群同构于曲面的甲板变换群(deck transformation group)。商空间的陪集有标准多边形做为代表元素。在下面,注意所有黎曼曲面都是可定向的。
度量基本多边形[编辑]
给定上半平面H中一点 ,以及PSL(2,R)一个离散子群Γ 自由不连续作用在上半平面,则我们可定义度量基本多边形(metric fundamental polygon)为点集
,以及PSL(2,R)一个离散子群Γ 自由不连续作用在上半平面,则我们可定义度量基本多边形(metric fundamental polygon)为点集

这里d是上半平面的双曲度量。度量基本多边形有时也称为狄里克雷区域(Dirichlet region)或沃罗诺伊多边形(Voronoi polygon)。
- 这个基本多边形是一个基本区(fundamental domain)。
- 这个基本多边形是凸集,连接这个多边形的任何两点的测地线完全包含在多边形内部。
- F的直径小于或等于H/Γ的直径。特别地,F的闭包紧。
- 如果Γ在H中没有不动点且H/Γ紧,则F的边数有限。
- 多边形的每条边是一个测地线。
- 对多边形的每条边s,恰有另外一条边s' 使得gs=s' 对某个g属于Γ。从而这个多边形有偶数条边。
- 将边两两连接的群元素集合g是Γ的生成元,没有更小的集合可生成Γ。
- F的闭包在Γ的作用下铺满上半平面。即
 这里
这里 是F的闭包。
是F的闭包。
标准基本多边形[编辑]
给定任何度量基本多边形F,用有限步可以构造另一个基本多边形,标准基本多边形(standard fundamental polygon),它具有额外一组值得注意的性质:
- 标准多边形的顶点都是等价的。“顶点”是说两条边相交的点。“等价”意味着每个顶点可以由Γ中某个g变到任何其它一个顶点。
- 边数可被4整除。
- Γ中一个给定元素g至多将多边形的一条边变到另一边。从而这些边可以成对标记出来。由于Γ的作用保持定向,如果一条边为
 ,则这一对中另一个可以标记为相反的方向
,则这一对中另一个可以标记为相反的方向 。
。
- 可以安排标准多边形的边,使得相邻边取形式
 。这就是说边对可安排成以这样的方式相间出现。
。这就是说边对可安排成以这样的方式相间出现。
- 标准多边形是凸集。
- 边可以安排成测地线。
上面的构造足够保证多边形的每条边在流形H/Γ中是一个闭(非平凡)环路。就其本身而言,每条边可以为基本群 中一个元素。特别地,基本群
中一个元素。特别地,基本群 有2n个生成元素
有2n个生成元素 ,由一个约束定义,
,由一个约束定义,

所得流形H/Γ的亏格是n。
例子[编辑]
度量基本多边形与标准多边形通常有不同的边数。比如,环面的标准基本多边形是一个基本平行四边形(fundamental parallelogram)。相比而言,度量基本多边形有六条边,是一个六边形。只需注意到六边形的边垂直平分平行四边形的边就可以看出来。这就是,取格中一点,然后考虑连接这点与邻点的直线之集合。每个这样的线被另一条垂直线平分,被这样的第二个线集合围住的最小的空间是一个六边形。
事实后,上一个构造一般都可行:取一点x,然后对Γ中g,考虑x与gx之间的测地线。平分这些测地线是另一个曲线集合,这些点的轨迹与x和gx距离相等。由第二个线集合围住的最小区域是度量基本多边形。
面积[编辑]
标准基本多边形的面积是 ,这里n是黎曼曲面的亏格(等价于4n是多边形的边数)。由于标准多边形是H/Γ的一个代表,黎曼曲面的整个面积等于标准多边形的面积。这个面积公式由高斯-博内定理得出,在某种意义下黎曼-赫尔维茨公式(Riemann-Hurwitz formula)是其推广。
,这里n是黎曼曲面的亏格(等价于4n是多边形的边数)。由于标准多边形是H/Γ的一个代表,黎曼曲面的整个面积等于标准多边形的面积。这个面积公式由高斯-博内定理得出,在某种意义下黎曼-赫尔维茨公式(Riemann-Hurwitz formula)是其推广。
标准多边形的具体形式[编辑]
对标准多边形可以给出具体表达式。一个更有用的形式是使用与这个标准多边形关联的群 。对一个亏格n定向曲面,群可由2n格生成元
。对一个亏格n定向曲面,群可由2n格生成元 给出。这些生成元由下列分式线性变换作用在上半平面给出。
给出。这些生成元由下列分式线性变换作用在上半平面给出。
对 :
:

参数由

和

以及

给出。可以验证这些生成元服从约束

这给出整个群呈示。
在高維,基本多变形的想法体现为齐性空间。
参考文献[编辑]
- Alan F. Beardon, The Geometry of Discrete Groups (1983), Springer-Verlag, New York. ISBN 0-387-90788-2.
- Hershel M. Farkas and Irwin Kra, Riemann Surfaces (1980), Springer-Verlag, New York. ISBN 0-387-90465-4.
- Jurgen Jost, Compact Riemann Surfaces (2002), Springer-Verlag, New York. ISBN 3-540-43299-X.













































