ド・モルガンの法則ほうそく

ド・モルガンの法則ほうそくのベン図べんずによる表現ひょうげん。図ず1、図ず2のそれぞれの場合ばあいにおいて、等式とうしきの両辺りょうへんの集合しゅうごうは青あおい領域りょういきで図示ずしされる。

ド・モルガンの法則ほうそく（ド・モルガンのほうそく、英えい: De Morgan's laws）は、ブール論理ろんりや集合しゅうごうの代数だいすう学がくにおいて、論理ろんり和わと論理ろんり積せきと否定ひてい（集合しゅうごうのことばでは、和わ集合しゅうごうと共通きょうつう部分ぶぶんと差さ集合しゅうごう）の間あいだに成なり立たつ規則きそく性せいである。名前なまえは数学すうがく者しゃオーガスタス・ド・モルガン（Augustus de Morgan, 1806–1871）にちなむ。

この規則きそく性せい（論理ろんりのことばで言いうと「真しんと偽にせを入いれ替かえ、論理ろんり和わと論理ろんり積せきを入いれ替かえた論理ろんり体系たいけい」）は、元もとの論理ろんり体系たいけいと同一どういつ視しできる、ということであるので、ド・モルガンの双対そうつい性せい（英えい: De Morgan's duality）と呼よばれることもある。

命題めいだい論理ろんりにおける法則ほうそく

任意にんいの命題めいだい $P,Q\in \{\bot ,\top \}$ に対たいして

$\neg (P\lor Q)=\neg P\land \neg Q\,,$

$\neg (P\land Q)=\neg P\lor \neg Q$

が成なり立たつ。これをド・モルガンの法則ほうそくという。

より一般いっぱん的てきな法則ほうそくとして、任意にんいの n 個この命題めいだい $P_{1},P_{2},\cdots ,P_{n}\in \{\bot ,\top \}$ に対たいして

$\neg \left(\bigvee _{i=1}^{n}P_{i}\right)=\bigwedge _{i=1}^{n}\neg P_{i}\,,\quad \neg \left(\bigwedge _{i=1}^{n}P_{i}\right)=\bigvee _{i=1}^{n}\neg P_{i}$

が成なり立たつ。

例れい

次つぎの命題めいだい

「私わたしの身長しんちょうは160cm以上いじょうであり、かつ私わたしの体重たいじゅうは50kg以上いじょうである」

の否定ひてい、すなわち

「「私わたしの身長しんちょうは160cm以上いじょうであり、かつ私わたしの体重たいじゅうは50kg以上いじょうである」ではない」

は、ド・モルガンの法則ほうそくによれば、次つぎの命題めいだいと等ひとしい。

「私わたしの身長しんちょうは160cm未満みまんである、または私わたしの体重たいじゅうは50kg未満みまんである」

同おなじようにして

「このボールは青あおいか、または赤あかい」

の否定ひていは

「このボールは青あおくなく、かつ赤あかくない」

になる。

述語じゅつご論理ろんりにおける法則ほうそく

D を空そらでない任意にんいの対象たいしょう領域りょういきとする。任意にんいの 1 変数へんすうの述語じゅつご $F:D\to \{\bot ,\top \}$ に対たいして

$\neg \,\forall x\,F(x)\,=\,\exists x\,\neg \,F(x)\,,$

$\neg \,\exists x\,F(x)\,=\,\forall x\,\neg \,F(x)$

が成なり立たつ。これをド・モルガンの法則ほうそくという。

$D=\{a_{1},a_{2},\cdots ,a_{n}\}$（有限ゆうげん集合しゅうごう）である場合ばあいは、これは

$\neg \left(\bigwedge _{i=1}^{n}F(a_{i})\right)=\bigvee _{i=1}^{n}\neg \,F(a_{i})\,,\quad \neg \left(\bigvee _{i=1}^{n}F(a_{i})\right)=\bigwedge _{i=1}^{n}\neg \,F(a_{i})$

と変形へんけいできる。

例れい

F(x) を変数へんすう x についての言明げんめいとすると

• 「全すべての x に対たいし F(x)」の否定ひていは「ある x が存在そんざいして ￢F(x)」
• 「ある x が存在そんざいして F(x)」の否定ひていは「全すべての x に対たいし ￢F(x)」

と表現ひょうげんできる。具体ぐたい例れいを挙あげると、

• 「全すべての人ひとが冷蔵庫れいぞうこを持もっている」の否定ひていは「ある人ひとは冷蔵庫れいぞうこを持もっていない」（すなわち、「冷蔵庫れいぞうこを持もっていない人ひとが少すくなくとも一人ひとりいる」）
• 「ある人ひとが冷蔵庫れいぞうこを持もっている」（すなわち、「冷蔵庫れいぞうこを持もっている人ひとが少すくなくとも一人ひとりいる」）の否定ひていは「全すべての人ひとが冷蔵庫れいぞうこを持もっていない」（すなわち、「誰だれひとりとして冷蔵庫れいぞうこを持もっていない」）

などである。また、後述こうじゅつするように部分ぶぶん否定ひていや全ぜん否定ひていのい換いかえも述語じゅつご論理ろんりにおけるド・モルガンの法則ほうそくを表現ひょうげんしていると考かんがえられる。

全ぜん否定ひていと部分ぶぶん否定ひてい

全ぜん否定ひていや部分ぶぶん否定ひていをどうい換いかえるかという問題もんだいは（述語じゅつご論理ろんりにおける）ド・モルガンの法則ほうそくが扱あつかう問題もんだいと本質ほんしつ的てきには同おなじである。

例たとえば x が本ほんを表あらわす変数へんすうとして、「本ほん x が好すきだ」という言明げんめいを A(x) と書かくことにすると、肯定こうてい文ぶん「すべての本ほんが好すきだ」は「全すべての x に対たいし A(x)」となる。

この文ぶんの部分ぶぶん否定ひてい「すべての本ほんを好すきだというわけではない」は「全すべての x に対たいし A(x)」の否定ひていであり、ド・モルガンの法則ほうそくによって「ある x に対たいし ￢A(x)」、すなわち「好すきでない本ほんもある」となる。全ぜん否定ひていの文ぶん「すべての本ほんが嫌きらいだ」は「全すべての x に対たいし ￢A(x)」と表あらわせ、ド・モルガンの法則ほうそくによって「ある x に対たいし A(x)」の否定ひてい、「好すきな本ほんはない」ということになる。

束論そくろんにおける法則ほうそく

L を任意にんいのブール代数だいすうとする。任意にんいの $x,y\in L$ に対たいして

$(x\cup y)^{c}=x^{c}\cap y^{c}\,,$

$(x\cap y)^{c}=x^{c}\cup y^{c}$

が成なり立たつ。これをド・モルガンの法則ほうそくという。

$\{a_{\lambda }|\lambda \in \Lambda \}$ を L の任意にんいの部分ぶぶん集合しゅうごうとする。$\textstyle \sup _{\lambda \in \Lambda }a_{\lambda }$ が存在そんざいするとき、$\textstyle \inf _{\lambda \in \Lambda }a_{\lambda }^{c}$ も存在そんざいし、

$\left(\sup _{\lambda \in \Lambda }a_{\lambda }\right)^{c}=\inf _{\lambda \in \Lambda }a_{\lambda }^{c}$

が成なり立たつ。また、$\textstyle \inf _{\lambda \in \Lambda }a_{\lambda }$ が存在そんざいするとき、$\textstyle \sup _{\lambda \in \Lambda }a_{\lambda }^{c}$ も存在そんざいし、

$\left(\inf _{\lambda \in \Lambda }a_{\lambda }\right)^{c}=\sup _{\lambda \in \Lambda }a_{\lambda }^{c}$

が成なり立たつ。これをド・モルガンの一般いっぱん法則ほうそくという。

例れい

二元にげん集合しゅうごう $L=\{\bot ,\top \}$ をブール代数だいすう、$\bot$ を最小さいしょう元もととすれば、$\top$ は最大さいだい元もととなる。そのとき、最小さいしょう元もと $\bot$ は偽にせな命題めいだい、最大さいだい元もと $\top$ は真まな命題めいだい、結むすび ∪ は論理ろんり和わ ∨、交まじわり ∩ は 論理ろんり積せき ∧ 、補元ほげん c は否定ひてい ￢ を表あらわすことになる。そして、ブール代数だいすうに関かんするド・モルガンの一般いっぱん法則ほうそくから、命題めいだい論理ろんりに関かんするド・モルガンの法則ほうそくを導みちびくことができる。

また、空そらでない任意にんいの集合しゅうごう（対象たいしょう領域りょういき）D を一ひとつ固定こていして考かんがえれば、D から L への写像しゃぞうは 1 変数へんすうの述語じゅつごとなり、全ぜん称しょう命題めいだい $\forall x$ や存在そんざい記号きごう $\exists x$ を定義ていぎすることができる。そして、ブール代数だいすうに関かんするド・モルガンの一般いっぱん法則ほうそくから、述語じゅつご論理ろんりに関かんするド・モルガンの法則ほうそくを導みちびくことができる。

直観ちょっかん主義しゅぎ論理ろんりにおける法則ほうそく

直観ちょっかん主義しゅぎ論理ろんりにおいてはド・モルガンの法則ほうそくは必かならずしも成なりたない。しかし、直観ちょっかん主義しゅぎ論理ろんり（LJ）においても以下いかのシークエント計算けいさんは証明しょうめい可能かのうである。

• $\,\neg ({\mathfrak {A}}\lor {\mathfrak {B}})\,\rightarrow \,\neg {\mathfrak {A}}\land \neg {\mathfrak {B}}$
• $\,\neg {\mathfrak {A}}\land \neg {\mathfrak {B}}\,\rightarrow \,\neg ({\mathfrak {A}}\lor {\mathfrak {B}})$
• $\,\neg {\mathfrak {A}}\lor \neg {\mathfrak {B}}\,\rightarrow \,\neg ({\mathfrak {A}}\land {\mathfrak {B}})$
• $\,\neg \,\exists x\,{\mathfrak {F}}(x)\,\rightarrow \,\forall x\,\neg \,{\mathfrak {F}}(x)$
• $\,\forall x\,\neg \,{\mathfrak {F}}(x)\,\rightarrow \,\neg \,\exists x\,{\mathfrak {F}}(x)$
• $\,\exists x\,\neg \,{\mathfrak {F}}(x)\,\rightarrow \,\neg \,\forall x\,{\mathfrak {F}}(x)$

集合しゅうごう論ろんにおける法則ほうそく

一般いっぱん的てきな集合しゅうごうの代数だいすう学がくでは、

${\overline {(P\cup Q)}}={\overline {P}}\cap {\overline {Q}}$

${\overline {(P\cap Q)}}={\overline {P}}\cup {\overline {Q}}$

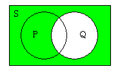
となる（ただし、￣は全体ぜんたい集合しゅうごうに対たいする補ほ集合しゅうごうを表あらわしている）。ベン図べんずを用もちいると第だい一式いっしきが正ただしいことが次つぎのようにして分わかる。

• 
  $P\cup Q$
• 
  ${\overline {(P\cup Q)}}$

• 
  ${\overline {P}}$
• 
  ${\overline {Q}}$
• 
  ${\overline {P}}\cap {\overline {Q}}$

詳細しょうさいは「差さ集合しゅうごう#ド・モルガンの法則ほうそく」を参照さんしょう

参考さんこう文献ぶんけん

• 前原まえはら, 昭二しょうじ『復刊ふっかん 数すう理論りろん理学りがく序説じょせつ』共立きょうりつ出版しゅっぱん、2010年ねん。ISBN 9784320019430。 

関連かんれん項目こうもく

• 負ふ論理ろんり
• 真理しんり関数かんすう

外部がいぶリンク

• 世界せかい大だい百科ひゃっか事典じてん『ド・モルガンの法則ほうそく』 - コトバンク
• Weisstein, Eric W. "de Morgan's Laws". mathworld.wolfram.com (英語えいご).
• Weisstein, Eric W. "de Morgan's Duality Law". mathworld.wolfram.com (英語えいご).