 平行な線路は無限遠にある消失点で交わる。
平行な線路は無限遠にある消失点で交わる。
数学における射影平面(しゃえいへいめん、英: projective plane)とは、初等的な平面の概念を拡張する幾何学的な構成のことである。通常の平面においては、二直線は典型的には一つの交点を持つが、特定の直線の組(平行線)は交点を持たない。一方、射影平面においては、通常の平面に「無限遠点」が追加され、平行線は無限遠点で交点を持つ。従って、射影平面では任意の相異なる二直線がただ一点において交わる。
射影平面の定義としてよく用いられるものが二種類ある。ひとつは線型代数学から来るもので、この場合の射影平面は、適当な古典群(英語版)に対する等質空間として与えられる。この場合の重要な例として、実射影平面(英語版)[1][2] RP2 および複素射影平面(英語版) CP2 が挙げられる。もうひとつは、もっと一般の公理的幾何学(英語版)および有限幾何学の立場により与えられる定義である。これは平面幾何学の接続的性質の研究に適している。
射影平面の概念は、もっと高次元の射影空間の概念に一般化される。射影平面は二次元の射影空間である。
線型代数学的には、射影平面は「三次元空間内の原点を通る直線全体の成す集合」として与えられる。射影平面上の直線は三次元空間内の原点を通る平面から生じる。きちんと述べれば、以下のようになる[3]。
K を任意の可除環(斜体)とし、 K 3 を K の元の三つ組 x = (x 0, x 1, x 2) 全体の成す集合(直積集合)とする。K 3 の零ベクトルでない任意の点 x に対し、原点と x を通る K 3 内の「直線」とは、 K 3 の部分集合

のことである。同様に K 3 の線型独立な点 x, y (つまり kx + ly = 0 ならば必ず k = l = 0)に対し、原点と x, y を通る「平面」とは、 K 3 の部分集合

のことであり、この平面は無数の直線を含む。
可除環 K 上の射影平面 KP2 とは、K 3 の原点を通る直線全体の成す集合をいう。KP2 の部分集合 L が、射影平面 KP2 内の(射影)直線であるとは、K 3 における平面で、それが含む直線全体の成す集合が KP2 においてちょうど L と一致するものが存在するときにいう。
少し異なる定義の仕方もあって、射影平面というのは集合 K 3 ∖ {(0, 0, 0)} を

で与えられる同値関係で割ったものである、ということもできる。この場合も射影平面内の直線は先ほどとまったく同じように定義できる。K が位相空間ならば KP2 にも(直積位相、部分空間の位相、商位相を通じて)内在的な位相が入る。
KP2 における座標系 (x 0, x 1, x 2) は斉次座標系 (homogeneous coordinates) と呼ばれる。各三つ組 (x 0, x 1, x 2) は KP2 の点を矛盾無く表すが、三つ組 (0, 0, 0) だけは例外で KP2 のどの点にも対応しない。K が有限体でない限り KP2 の各点に対応する三つ組は無数に存在しうる。
- K として位数 p n の有限体を取れば、p 2n + p n + 1 個の点を持つ射影平面が得られる。後述するファノ平面は p n = 2 とした場合にあたる。
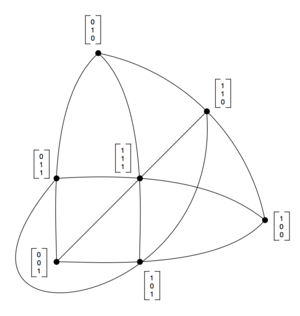 平面 F22 上の平行な直線に対して無限遠点を付け加えると、すべての相異なる直線が一点で必ず交わるファノ平面(英語版) PG(2, 2) = F2P2 が得られる。
平面 F22 上の平行な直線に対して無限遠点を付け加えると、すべての相異なる直線が一点で必ず交わるファノ平面(英語版) PG(2, 2) = F2P2 が得られる。
体 K 上の通常の平面 K 2 は射影平面 KP2 へ写像

によって埋め込まれる。この写像の像の補集合は (0, x 1, x 2) なる形の点全体の成す集合であり、このような埋め込みが与えられているという観点によって、補集合の点は無限遠点を表している。無限遠点の全体は KP2 における直線を成す(つまり、この直線は K 3 における平面

から生じる)。直観的には、無限遠点というのは平行線の交わる所としての「余分な」点であり、点 (0, x 1, x 2) というのは傾きが x 2/x 1 であるような直線すべての交点に対応する。例えば、通常の平面 K 2 における二直線

を考えれば、これらの傾きはともに 0 であってこれらは交わらない。これらを先ほどの埋め込みによって KP2 の部分集合と見なせば、これらは KP2 における直線とはならないが、それぞれに点 (0, 1, 0) を加えた

は KP2 における直線となる。a は K3 における平面

から生じ、b は平面

から生じる。これらの射影直線 a, b は点 (0, 1, 0) において交わる。実は、K 2 における傾き 0 の直線はすべて、この方法で射影化したとき、KP2 の点 (0, 1, 0) において交わる。
先ほど与えた平面 K 2 の射影平面 KP2 への埋め込みは一意ではなく、それぞれの埋め込みごとにその無限遠点となる点は変わってくる。例えば、埋め込み

を考えれば、像の補集合に属する (x 0, 0, x 2) なる形の点が無限遠点と見なされる。
射影平面 KP2 における(射影)変換とは、KP2 からそれ自身への可逆な写像であって、直線を直線に写すものをいう。斉次座標系を用いれば、これは 3-次正則行列 M を用いて

と書くことができる。二つの行列が同じ射影変換を定めるのは、一方が他方の定数倍であるときに限る。従って、射影変換全体の成す群は一般線型群の剰余群である。
いくつか線型代数学的な定義を挙げたが、いずれもより高次元の場合に拡張するのは容易である。d-次元射影空間 KPd は、K n+1 内の原点を通る直線全体の成す集合であり、KPd 内の直線は K n+1 の原点を通る平面に対応する。射影空間の概念はさらにグラスマン空間の概念へ一般化することができる。
より一般な組合せ論的定義によれば、射影平面は直線の集合と点の集合から成り、点と直線との間の結合あるいは接続 (incidence) と呼ばれる以下のような性質を持つ関係を備えるものである。
- 任意の異なる二点に対し、それらを接続する直線がただ一つ存在する。
- 任意の異なる二直線に対し、それらのいずれとも接続する点がただ一つ存在する。
- 平面上の四点で、そのうちの二点よりも多くに接続するような直線は一つも存在しない、というものが存在する。
条件2は平行線が存在しないことを意味する。また条件3は退化する場合(後述)を除くためだけにある。
射影平面においては、それが含む直線の数と点の数とが同じであることを示すことができる(有限でも無限でも)。有限射影平面は
- N2 + N + 1 個の点と、
- N2 + N + 1 本の直線を持ち、
- 各直線上に N + 1 個の点が載っていて、
- 各点を N + 1 本の直線が通る。
ここで、N ≥ 2 は射影平面の位数 (order) と呼ばれる整数である(有限幾何学も参照)。
前節に述べたような線型代数学的定義から生じる射影平面はどれも、本節に言う組合せ論的な定義に基づく射影平面として記述することができる。従って、位数 pn の有限体から、位数 N = pn の射影平面を与えることができる。
 ファノ平面: 平面上の「点」は黒丸、平面上の「直線」は線分または円として示される。
ファノ平面: 平面上の「点」は黒丸、平面上の「直線」は線分または円として示される。
ファノ平面は二元体から生じる射影平面である。これは最小の射影平面で、わずか七つの点と七つの直線から成る。右図では、七つの「点」を小さな黒丸で表し、七つの「直線」は六本の線分と一つの円で表したものだが、射影平面の双対性により(点と直線とを互いに入れ替えたものもやはり射影平面となるから)、黒丸を「直線」、線分と円を「点」と思うこともできる。この七つの点に対して置換を施すと、共線点(同一直線上にある点)を共線点へ移す変換を引き起こす。このことを以って、ファノ平面は「対称」であるという。
組合せ論的に定義される任意の射影平面に対して、平面三項環と呼ばれる座標「環」(ただし、本当に環となっているとは限らない)を対応させることができる。平面三項環は体または斜体になっている必要はなく、また斜体から構成することができない射影平面というものも多く存在する。そのような射影平面は非デザルグ的な射影平面と呼ばれ、未だ活発な研究の成されている研究対象である。
この平面三項環が持つ代数的性質は、それに対応して平面が持つ幾何学的な接続関係の性質に読み替えることができる。例えば、デザルグの定理に対応するのは座標環が斜体から得られるということであり、またパップスの定理が対応するのは座標環が可換体から得られるということである。あるいは(たとえば八元数体のように)必ずしも結合的でない交代的な可除代数から得られるようなものにはムーファン平面が対応する。
有限射影平面においてデザルグの定理がパップスの定理を含むという純粋に幾何学的な主張の、しかし唯一知られている証明は、斜体に成分を持つ座標をとってウェダーバーンの定理(有限可除環は必ず可換体である)を用いるという代数的な方法によってなされる(逆にパップスの定理がデザルグの定理を含むことは、(有限とは限らない)任意の射影平面において真であり、しかもこれは幾何学的に証明することができる)。
素数位数 N の射影平面は、位数 N の有限体上の線型代数学的構成を用いて構成することができる。あるいは以下のようにしても構成できる。
- 一点 P を用意する。
- N 個の点を用意して、c = 0, ..., N − 1 に応じて、P(c) と書く。
- 同様に N2 個の点を P(r, c) (r, c = 0, ..., N − 1) とする。
これらの点に対して、以下のように直線を構成する
- 一本の直線が L = {P, P(0), ..., P(N − 1)} で与えられる。
- N 本の直線を、c = 0, ..., N − 1 に応じて、L(c) = {P, P(0, c), ..., P(N − 1, c)} とする。
- N2 本の直線を L(r, c) = {P(c) および P((r + ci) mod N, i)} (i, r, c = 0, ..., N − 1) とする。
ただし、ここで書いた式
- (r + ci) mod N
で i が 0 から N − 1 までの全ての値を亘るのは、N が素数の場合に限る。
この構成から、二つの退化平面が生じる。すなわち、N = 0 に対してただ一つの点がただ一つの直線に接続したものが得られ、N = 1 に対して三点と三直線からなる三角形が得られる。素数 N に対しては、この方法で構成される任意の平面が上記定義の条件3を満足する。
例えば N = 2 とすると、
- 一直線 L = { P, P(0), P(1)}
- 二直線 L(c) = {P, P(0,c), P(1,c)} (c = 0, 1)
- 四直線 L(r, c) = {P(c), P((r + ci) mod 2, i) | i = 0, 1} (r, c = 0, 1)
となる。
既に説明したように、各素数冪 pn に対して同位数の射影平面が存在する。事実として、「知られている」全ての有限射影平面はその位数が素数冪である。
それ以外の位数についても有限射影平面が存在するかどうかというのは、未解決の問題である(有限射影平面の基本予想 Prime Power Conjecture)。位数に関する一般的な制限として知られているのは、位数 N が法 4 に関して 1 または 2 と合同ならば、それは二つの平方数の和にならなければいけないというブルック=ライザー=チョウラの定理である。これにより N = 6 が除外できる。次の場合は N = 10 が、大規模計算機の計算により除外された。それ以上の場合については知られていない(特に N = 12 も未解決である)。
位数 N の射影平面が存在するための必要十分条件は、位数 N のアフィン平面が存在することである。位数 N のアフィン平面がただ一つ存在するならば、位数 N の射影平面もただ一つ存在するが、逆は必ずしも真でない。
位数 N の射影平面はスタイナーの S(2, N + 1, N2 + N + 1)-系である(スタイナー系参照)。逆に N ≥ 2 に対するこの形のスタイナー系が射影平面となることが証明できる。
位数 N の互いに直交するラテン方格の総数は高々 N − 1 である。これが N − 1 となりうる必要十分条件は、その位数の射影平面が存在することである。
一方、射影平面の分類は全然終わっていない。いくつかの結果を位数の順に以下に示す。
- 2 : 全て PG(2,2) に同型
- 3 : 全て PG(2,3) に同型
- 4 : 全て PG(2,4) に同型
- 5 : 全て PG(2,5) に同型
- 6 : この位数の射影平面は存在しない(オイラーの士官36人の問題(英語版)として、タリーにより示された)。
- 7 : 全て PG(2,7) に同型
- 8 : 全て PG(2,8) に同型
- 9 : PG(2,9) および三種類の異なる(同型でない)非デザルグ平面
- 10 : この位数の射影平面は存在しない(計算機による膨大な計算の結果として証明された)。
- 11 : すくなくとも PG(2,11) が挙げられる。他は知られていないが可能性はある。
- 12 : この位数の射影平面は存在しないと予想されているが証明はされていない。
退化平面とは、上述の定義における条件3を満足しない場合である。退化平面には二つの系列がある。
- 任意個数の点 P1, ..., Pn および直線 L1, ..., Lm が以下を満たすもの。
- L1 = { P1, P2, ..., Pn}
- L2 = { P1 }
- L3 = { P1 }
- …
- Lm = { P1 }
- 任意個数の点 P1, ..., Pn および直線 L1, ..., Ln が以下を満たすもの(点の数と直線の数は同数である)。
- L1 = { P2, P3, ..., Pn }
- L2 = { P1, P2 }
- L3 = { P1, P3 }
- …
- Ln = { P1, Pn }
接続関係を用いた定義も、二次元より高次元の射影幾何における対応物を考えることができる。高次元化したものは、平面の場合ほどには興味深い性質を示さず(平面の場合よりもよく振舞うといってもよいが)、つまり斜体上の古典的な射影空間となる。そうなる理由は別な場所で述べるほうが適切であろうけれども、高次元射影空間における接続の性質を用いて幾何学的にデザルグの定理を示せる(つまり、座標環が斜体となる)ことによる。
- Albert, A. Adrian; Sandler, Reuben (1968), An Introduction to Finite Projective Planes, New York: Holt, Rinehart and Winston
- John C. Baez, "The Octonions", Bull. Amer. Math. Soc. 39 (2002), 145-205. Available electronically.[1]
- Glen E. Bredon (1993). Topology and Geometry. Springer-Verlag. ISBN 0-387-97926-3
- Dembowski, Peter (1968), Finite Geometries, Berlin: Springer Verlag
- D. Hughes and F. Piper (1973). Projective Planes. Springer-Verlag. ISBN 0-387-90044-6
- Kárteszi, F. (1976), Introduction to Finite Geometries, Amsterdam: North-Holland, ISBN 0-7204-2832-7
- Clement W.H. Lam, "The Search for a Finite Projective Plane of Order 10", American Mathematical Monthly 98, (no. 4) 1991, pp. 305 – 318.
- Lindner, Charles C. and Christopher A. Rodger (eds.) Design Theory, CRC-Press; 1 edition (October 31, 1997). ISBN 0-8493-3986-3.
- Lüneburg, Heinz (1980), Translation Planes, Berlin: Springer Verlag, ISBN 0-387-09614-0
- Weisstein, Eric W. "Projective plane". mathworld.wolfram.com (英語).
- G. Eric Moorhouse, Projective Planes of Small Order, (2003)
- Room, T. G.; Kirkpatrick, P. B. (1971), Miniquaternion Geometry, Cambridge: Cambridge University Press, ISBN 0-521-07926-8
- I. R. Shafarevich (1994). Basic Algebraic Geometry. Springer-Verlag. ISBN 0-387-54812-2
- Stevenson, Frederick W. (1972), Projective Planes, San Francisco: W.H. Freeman and Company, ISBN 0-7167-0443-9














