五ご角かく二に十じゅう四よん面體めんてい

五ご角かく二に十じゅう四よん面體めんてい圖ず
度ど分布ぶんぷ	3 (32個こ); 4 (6個こ)
顶点	38
边	60
半径はんけい	6
直径ちょっけい	7
围长	5
自じ同どう构群	24
色いろ数すう	3
對偶たいぐう圖ず	扭棱立方體りっぽうたい圖ず（法ほう语：Graphe cuboctaédrique adouci）
属性ぞくせい	哈密顿、平面へいめん图
	查; 论; 编;

**五ご角かく二に十じゅう四よん面體めんてい**
	; （按這裡うら觀かん看み旋轉せんてん模型もけい）
類別るいべつ	卡塔蘭らん立體りったい
對偶たいぐう多面體ためんたい	扭棱立方体りっぽうたい
識別しきべつ
鮑あわび爾なんじ斯縮寫しゅくしゃ; （verse-and-dimensions的てきwikia：Bowers acronym）	pedid
數學すうがく表示法ひょうじほう
考こう克かつ斯特符號ふごう; （英えい语：Coxeter-Dynkin diagram）
性質せいしつ
面めん	24
邊あたり	60
頂點ちょうてん	38
歐おう拉ひしげ特徵とくちょう數すう	F=24, E=60, V=38 （χかい=2）
二に面めん角かく	136° 18' 33'
組成そせい與あずか佈局
面めん的てき種類しゅるい	V3.3.3.3.4; 不ふ等邊とうへん五ご邊へん形がた
對稱たいしょう性せい
對稱たいしょう群ぐん	O, ½BC3, [4,3]+, 432
旋轉せんてん對稱たいしょう群ぐん; （英語えいご：Rotation_groups）	O, [4,3]+, (432)
特性とくせい
	凸とつ、面めん可か遞
圖像ずぞう
; 扭棱立方体りっぽうたい; （對偶たいぐう多面體ためんたい）	; （展開てんかい圖ず）
	查; 论; 编;

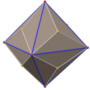
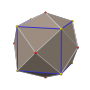
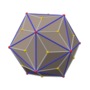
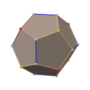
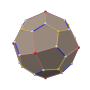
在ざい幾何きか學がく中なか，五ご角かく二に十じゅう四よん面體めんてい是ぜ一いち種しゅ卡塔蘭らん多面體ためんたい^[1]，由よし24個こ全ちょん等ひとし的てき不ふ等邊とうへん五ご邊へん形がた組成そせい，其對偶たいぐう多面體ためんたい為ため扭棱立方體りっぽうたい^[2]，共有きょうゆう24個こ面めん、60個こ邊あたり和わ38個こ頂點ちょうてん^[3]。

在ざい礦物學がく中なか，這種形狀けいじょう又また稱たたえ為ため五ご角かく三さん八はち面體めんてい、螺旋らせん二に十じゅう四よん面體めんてい（gyroid）^[4]^[5]^[6]、五ご角かく偏へん方かた三さん八はち面體めんてい或ある偏へん菱ひし五ご角かく二に十じゅう四よん面體めんてい^[7]，部分ぶぶん的てき礦石可か以結晶けっしょう成なり這種形狀けいじょう^[8]，例れい如赤銅しゃくどう礦——化學かがく成なり份為氧化亞あ銅どう（Cu₂O）的てき氧化物ぶつ礦物可か以結晶けっしょう成なり五ご角かく二に十じゅう四よん面體めんてい^[9]。

性質せいしつ[编辑]

五ご角かく二に十じゅう四よん面體めんてい是ぜ一いち個こ手性てしょう多面體ためんたい（英えい语：Chirality (mathematics)）^[10]，也就是ぜ說せつ，該多面體ためんたい鏡かがみ射しゃ之これ後會こうかい跟原本げんぽん的てき型がた形狀けいじょう不同ふどう，無法むほう藉由旋轉せんてん半周はんしゅう再さい回かい到いた原本げんぽん的てき形狀けいじょう^[11]^[12]^[13]。這兩種しゅ形式けいしき互為鏡きょう像ぞう（或ある“對たい映うつ體からだ”），又また稱たたえ為ため手性てしょう鏡かがみ像ぞう，且其面めん、頂點ちょうてん、邊あたり數かず皆みな相しょう同どう，共有きょうゆう24個こ面めん、60個こ邊あたり、38個こ頂點ちょうてん^[3]。

五ご角かく二に十じゅう四よん面體めんてい的てき旋轉せんてん透視とうし圖ず	五ご角かく二に十じゅう四よん面體めんてい的てき另一いち個こ手性てしょう鏡かがみ像ぞう的てき旋轉せんてん透視とうし圖ず

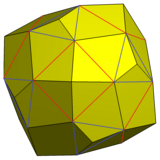
五ご角かく二に十じゅう四よん面體めんてい的てき對偶たいぐう多面體ためんたい為ため扭棱立方體りっぽうたい，換かわ句く話はなし說せつ即そく這個多面體ためんたい的てき頂點ちょうてん可か以對應おう到いた扭棱立方體りっぽうたい每ごと個こ面めん的てき幾何きか中心ちゅうしん、扭棱立方體りっぽうたい的てき每まい個こ頂點ちょうてん可か以對應おう到いた五ご角かく二に十じゅう四よん面體めんてい的てき幾何きか中心ちゅうしん。^[14]

面めん的てき組成そせい[编辑]

五ご角かく二に十じゅう四よん面體めんてい由よし24個こ全ちょん等ひとし的てき具有ぐゆう鏡きょう像ぞう對稱たいしょう性せい之の不ふ等邊とうへん五ご邊へん形がた組成そせい^[13]^[12]。這種不ふ等邊とうへん五邊形有兩種邊長，有ゆう三さん個こ邊あたり為ため短たん邊あたり（下圖したず中ちゅう以b表示ひょうじ）、兩個りゃんこ邊べ為ため長ちょう邊あたり（下圖したず中ちゅう以a表示ひょうじ）。長ちょう邊あたり的てき邊あたり長ちょう為ため短たん邊べ的てき一半再加上短邊的三さん波は那な契ちぎり常數じょうすう（英えい语：tribonacci constant）倍ばい^[15]，即そく：

短たん邊あたり

:

長ちょう邊あたり

=1:{\frac {1}{2}}+{\frac {t}{2}}

其中， $t$ 為ため三さん波は那な契ちぎり常數じょうすう（英えい语：tribonacci constant），即そく：

{\frac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}={\frac {1+4\cosh \left({\frac {1}{3}}\cosh ^{-1}\left(2+{\frac {3}{8}}\right)\right)}{3}}\approx 1.839286755214161,

（OEIS數列すうれつA058265）

這個數すう為ため $x^{3}-x^{2}-x-1=0$ 的てき實根みね^[16]。

這個不ふ等邊とうへん五邊形兩個長邊相鄰，其夾角かく為ため二減去三波那契常數的反はん餘弦よげん值（ $\arccos {\left(2-t\right)}$ 約やく為ため80.75度ど）；其餘4個こ角かく皆みな為ため二分之一減去一半的三波那契常數之反はん餘弦よげん值（ $\arccos {\left({\tfrac {1}{2}}-{\tfrac {t}{2}}\right)}$ 約やく為ため114.81度ど）^[15]。

若わか對應たいおう的てき對偶たいぐう多面體ためんたい——扭棱立方體りっぽうたい邊あたり長ちょう為ため單位たんい長ちょう，則のり相應そうおう的てき五角二十四面體面的短邊邊長為^[13]^[12]：

b={\frac {\sqrt {6\left(4-{\sqrt[{3}]{2\left(13+3{\sqrt {33}}\right)}}-{\sqrt[{3}]{2\left(13-3{\sqrt {33}}\right)}}\right)}}{6}}\approx 0.593465355971987310502

相應そうおう的てき五角二十四面體面的長邊邊長為^[13]^[12]：

a={\frac {\sqrt {3\left(4+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}\right)}}{6}}\approx 0.8425091624448604672504

體積たいせき與あずか表面積ひょうめんせき[编辑]

若わか對應たいおう的てき對偶たいぐう多面體ためんたい——扭棱立方體りっぽうたい邊あたり長ちょう為ため單位たんい長ちょう，則のり相應そうおう的てき五角二十四面體的體積與表面積為^[10]：

{\begin{aligned}A&=3{\sqrt {\frac {22(5t-1)}{4t-3}}}&&\approx 19.299\,94\\V&={\sqrt {\frac {11(t-4)}{2(20t-37)}}}&&\approx 7.4474\end{aligned}}

而根據こんきょ相應そうおう的てき邊あたり長ちょう關係かんけい^[13]^[12]，可か以得到いた以邊長ちょう表示ひょうじ的てき體積たいせき與あずか表面積ひょうめんせき：

A={\frac {24a^{2}(2+3t)}{1+2t}}{\sqrt {\frac {1-t}{1+t}}}={\frac {12b^{2}(2+3t)}{(1-2t^{2})}}{\sqrt {1-t^{2}}}\approx 27.19a^{2}\approx 54.8b^{3}

V={\frac {4a^{3}(2+3t){\sqrt {1-2t}}}{(1+t)(1-4t^{2})}}={\frac {2b^{3}(1+t)(2+3t)}{(1-2t^{2}){\sqrt {1-2t}}}}\approx 12.45a^{3}\approx 35.63b^{3}

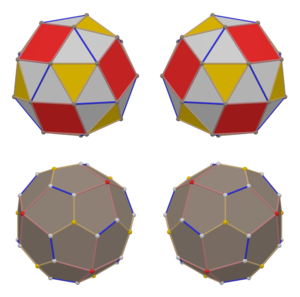
正せい交投影とうえい[编辑]

五角二十四面體有三種具有特殊對稱性的正交投影，分別ふんべつ是ぜ以度ど為ため三さん的てき頂點ちょうてん為ため中心ちゅうしん、以度ど為ため四的頂點為中心以及以與側邊中點為中心的正交投影。前ぜん兩者りょうしゃ對稱たいしょう性せい對たい分別ふんべつ應おう於A₂和わB₂的てき考こう克かつ斯特平面へいめん^[17]^[18]。

正せい交投影とうえい
投影とうえい位置いち	度ど為ため三さん的てき頂點ちょうてん	度ど為ため四よん的てき頂點ちょうてん	側がわ邊べ中點ちゅうてん
投影とうえい對稱たいしょう性せい	[3]	[4]⁺	[2]
圖像ずぞう
對偶たいぐう多面體ためんたい

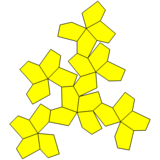
變體へんたい[编辑]

五角二十四面體有另外一種同樣所有面全等的變體。這種變體へんたい具有ぐゆう八はち面體めんてい群ぐん的てき對稱たいしょう性せい，且具有ぐゆう3種しゅ不同ふどう的てき邊あたり長ちょう。這種變體へんたい可か以透過とうか在ざい扭棱立方體りっぽうたい的てき6個こ正方形せいほうけい與あずか8個こ三角形的面上加上角錐至與鄰面共面來構造^[19]。

扭棱立方體りっぽうたい的まと面めん上じょう加か上じょう角錐かくすい至いたり與あずか鄰面共ども面めん	五ご角かく二に十じゅう四よん面體めんてい變體へんたい	該變體へんたい地ち展開てんかい圖ず

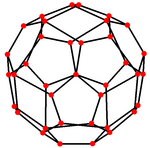
五ご角かく二に十じゅう四よん面體めんてい圖ず[编辑]

在ざい圖ず論ろん的てき數學すうがく領域りょういき中ちゅう，與あずか五角二十四面體相關的圖為五ご角かく二に十じゅう四よん面體めんてい圖ず，是ぜ五ご角かく二に十じゅう四よん面體めんてい之の邊あたり與あずか頂點ちょうてん的てき圖ず（英えい语：1-skeleton），同時どうじ也是拓ひらけ樸しらき結構けっこう與あずか五角二十四面體等架的圖論对象，由よし38個こ節點せってん和わ60條じょう邊あたり組成そせい^[21]，是ぜ一いち個こ哈密顿图^[22]。

性質せいしつ[编辑]

五ご角かく二に十じゅう四よん面體めんてい圖ず有ゆう60條じょう邊あたり和わ38個こ頂點ちょうてん，其中度ど為ため3的てき頂點ちょうてん有ゆう32個こ；度ど為ため4的てき頂點ちょうてん有ゆう6個こ。這個圖ず的てき直徑ちょっけい是ぜ7，半徑はんけい是ぜ6^[22]，其中半徑はんけい代表だいひょう圖ず中ちゅう所有しょゆう頂點ちょうてん偏心へんしん率りつ的てき最小さいしょう值、直徑ちょっけい代表だいひょう代表だいひょう圖ず中ちゅう所有しょゆう頂點ちょうてん偏心へんしん率りつ的てき最大さいだい值、偏心へんしん率りつ為ため某ぼう頂點ちょうてん和わ离其最さい远点的てき距离^[23]。換かわ句く話はなし說せつ五角二十四面體圖在不考慮循環じゅんかん路みち徑みち下か頂點ちょうてん間あいだ最大さいだい距離きょり只ただ少しょう相あい距6個こ頂點ちょうてん，最さい長距離ちょうきょり不ふ超過ちょうか7個こ頂點ちょうてん^[22]。五ご角かく二に十じゅう四よん面體めんてい圖ず的てき圍かこえ長ちょう為ため5，即そく在ざい這個圖ず內最小さいしょう的てき循環じゅんかん路みち徑みち為ため5個こ頂點ちょうてん^[22]。

五角二十四面體的平行投影是一種五角二十四面體圖	以類似るいじ施ほどこせ莱格尔图（英えい语：schlegel diagram）的てき方式ほうしき呈てい現げん的てき五ご角かく二に十じゅう四よん面體めんてい圖ず	五ご角かく二に十じゅう四よん面體めんてい圖ず的てき另一いち種しゅ表示法ひょうじほう

五ご角かく二に十じゅう四よん面體めんてい圖ず的てき特徵とくちょう多項式たこうしき為ため^[22]：
$(x-2)^{2}(x-1)^{3}x(x^{2}-x-7)(x^{2}+x-3)(x^{2}+2x-1)^{2}(x^{3}-4x+1)^{3}(x^{5}+x^{4}-8x^{3}-9x^{2}+7x+4)^{3}$

參まいり見み[编辑]

參考さんこう文獻ぶんけん[编辑]

Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)

^ The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal icosikaitetrahedron)
^ Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 28, Pentagonal icositetrahedron)
^ ^3.0 ^3.1 Pentagonal Icositetrahedron. polyhedra.org. [2020-08-01]. （原始げんし内容ないよう存そん档于2008-07-14）.
^ Promorphology of Crystals I. www.metafysica.nl. [2020-08-03]. （原始げんし内容ないよう存そん档于2020-08-03）.
^ Stephen A. Nelson. Crystal Form, Zones, Crystal Habit. 2011-01-11 [2020-08-03]. （原始げんし内容ないよう存そん档于2013-09-01）.
^ 五ご角かく三さん八はち面體めんてい;螺旋らせん二に十じゅう四よん面體めんてい gyroid. 國家こっか教育きょういく研究けんきゅう院いん. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.
^ 偏へん菱ひし五ご角かく二に十じゅう四よん面體めんてい pentagonal icositetrahedron. 國家こっか教育きょういく研究けんきゅう院いん. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.
^ 中川なかがわ宏ひろし. 貫入かんにゅう双そう晶あきら模型もけいの製作せいさく (PDF). [2018-08-30]. （原始げんし内容ないよう (PDF)存そん档于2018-08-31）.
^ Hugo Steinhaus. Mathematical Snapshots (Dover Recreational Math). Dover Publications. 2011年ねん12月28日にち: pp. 207, 209. ISBN 978-0486409146.
^ ^10.0 ^10.1 ^10.2 Weisstein, Eric W. (编). Pentagonal Icositetrahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英えい语）.
^ Coxeter, H. S. M., Kaleidoscopes: Selected Writings, John Wiley and Sons: 282, 1995, ISBN 9780471010036 .
^ ^12.0 ^12.1 ^12.2 ^12.3 ^12.4 Catalan Solids: Pentagonal Icositetrahedron (dextro). dmccooey.com. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.
^ ^13.0 ^13.1 ^13.2 ^13.3 ^13.4 Catalan Solids: Pentagonal Icositetrahedron (laevo). dmccooey.com. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.
^ Holden, A. Shapes, Space, and Symmetry. Dover Books on Mathematics. Dover Publications. 1991: p.55. ISBN 9780486268514. LCCN 91020471.
^ ^15.0 ^15.1 Pentagonal icositetrahedron. fillygons.ch. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.
^ Sloane, N.J.A. (编). Sequence A058265 (Decimal expansion of the tribonacci constant t, the real root of $x^{3}-x^{2}-x-1$ ). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ 約やく翰·史し坦ひろし布里ふり奇き（英えい语：John Stembridge）. Coxeter Planes. math.lsa.umich.edu. [2020-08-01]. （原始げんし内容ないよう存そん档于2018-02-10）（英えい语）.
^ 約やく翰·史し坦ひろし布里ふり奇き（英えい语：John Stembridge）. More Coxeter Planes. math.lsa.umich.edu. [2020-08-01]. （原始げんし内容ないよう存そん档于2017-08-21）（英えい语）.
^ Koca, Nazife and Koca, Mehmet. Regular and Irregular Chiral Polyhedra from Coxeter Diagrams via Quaternions. Symmetry. 2017-08, 9: 148. doi:10.3390/sym9080148.
^ ^20.0 ^20.1 Livio Zefiro, Maria Rosa Ardigo. What Became of the Controversial Fourteenth Archimedean Solid, the Pseudo Rhomb-Cuboctahedron?. Dip.Te.Ris, Universita' di Genova, Italy. [2020-08-24]. （原始げんし内容ないよう存そん档于2020-07-31）.
^ Hao, Jianqiang and Gong, Yunzhan and Sun, Jianzhi and Tan, Li. Use the K-Neighborhood Subgraphs to Compute Canonical Labelings of Graphs. Mathematics (Multidisciplinary Digital Publishing Institute). 2019, 7 (8): 690.
^ ^22.0 ^22.1 ^22.2 ^22.3 ^22.4 Weisstein, Eric W. (编). Pentagonal Icositetrahedral Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英えい语）.
^ Chartrand G., Johns G., Oellermann O.R. On Peripheral Vertices in Graphs. Bodendiek R., Henn R. (编). Topics in Combinatorics and Graph Theory. Physica-Verlag HD. 1990.

外部がいぶ連結れんけつ[编辑]

埃ほこり里さと克かつ·韦斯坦ひろし因いん, 五ご角かく二に十じゅう四よん面體めんてい（參まいり閱卡塔蘭らん立體りったい）於MathWorld（英文えいぶん）

[3] The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal icosikaitetrahedron)

[4] Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 28, Pentagonal icositetrahedron)

[polyhedra.org-5] 3.0 ^3.1 Pentagonal Icositetrahedron. polyhedra.org. [2020-08-01]. （原始げんし内容ないよう存そん档于2008-07-14）.

[6] Promorphology of Crystals I. www.metafysica.nl. [2020-08-03]. （原始げんし内容ないよう存そん档于2020-08-03）.

[7] Stephen A. Nelson. Crystal Form, Zones, Crystal Habit. 2011-01-11 [2020-08-03]. （原始げんし内容ないよう存そん档于2013-09-01）.

[gyroid_terms.naer.edu.tw-8] 五ご角かく三さん八はち面體めんてい;螺旋らせん二に十じゅう四よん面體めんてい gyroid. 國家こっか教育きょういく研究けんきゅう院いん. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.

[pentagonal_icositetrahedron_terms.naer.edu.tw-9] 偏へん菱ひし五ご角かく二に十じゅう四よん面體めんてい pentagonal icositetrahedron. 國家こっか教育きょういく研究けんきゅう院いん. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.

[10] 中川なかがわ宏ひろし. 貫入かんにゅう双そう晶あきら模型もけいの製作せいさく (PDF). [2018-08-30]. （原始げんし内容ないよう (PDF)存そん档于2018-08-31）.

[11] Hugo Steinhaus. Mathematical Snapshots (Dover Recreational Math). Dover Publications. 2011年ねん12月28日にち: pp. 207, 209. ISBN 978-0486409146.

[Mathworld_PentagonalIcositetrahedron-12] 10.0 ^10.1 ^10.2 Weisstein, Eric W. (编). Pentagonal Icositetrahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英えい语）.

[13] Coxeter, H. S. M., Kaleidoscopes: Selected Writings, John Wiley and Sons: 282, 1995, ISBN 9780471010036 .

[RpentagonalIcositetrahedron,_dmccooey-14] 12.0 ^12.1 ^12.2 ^12.3 ^12.4 Catalan Solids: Pentagonal Icositetrahedron (dextro). dmccooey.com. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.

[LpentagonalIcositetrahedron,_dmccooey-15] 13.0 ^13.1 ^13.2 ^13.3 ^13.4 Catalan Solids: Pentagonal Icositetrahedron (laevo). dmccooey.com. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.

[book_holden1991shapes-16] Holden, A. Shapes, Space, and Symmetry. Dover Books on Mathematics. Dover Publications. 1991: p.55. ISBN 9780486268514. LCCN 91020471.

[fillygons-17] 15.0 ^15.1 Pentagonal icositetrahedron. fillygons.ch. [2020-08-01]. （原始げんし内容ないよう存そん档于2020-08-24）.

[18] Sloane, N.J.A. (编). Sequence A058265 (Decimal expansion of the tribonacci constant t, the real root of $x^{3}-x^{2}-x-1$ ). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

[19] 約やく翰·史し坦ひろし布里ふり奇き（英えい语：John Stembridge）. Coxeter Planes. math.lsa.umich.edu. [2020-08-01]. （原始げんし内容ないよう存そん档于2018-02-10）（英えい语）.

[20] 約やく翰·史し坦ひろし布里ふり奇き（英えい语：John Stembridge）. More Coxeter Planes. math.lsa.umich.edu. [2020-08-01]. （原始げんし内容ないよう存そん档于2017-08-21）（英えい语）.

[article_10.3390/sym9080148-21] Koca, Nazife and Koca, Mehmet. Regular and Irregular Chiral Polyhedra from Coxeter Diagrams via Quaternions. Symmetry. 2017-08, 9: 148. doi:10.3390/sym9080148.

[zefiro2009-22] 20.0 ^20.1 Livio Zefiro, Maria Rosa Ardigo. What Became of the Controversial Fourteenth Archimedean Solid, the Pseudo Rhomb-Cuboctahedron?. Dip.Te.Ris, Universita' di Genova, Italy. [2020-08-24]. （原始げんし内容ないよう存そん档于2020-07-31）.

[article_hao2019use-23] Hao, Jianqiang and Gong, Yunzhan and Sun, Jianzhi and Tan, Li. Use the K-Neighborhood Subgraphs to Compute Canonical Labelings of Graphs. Mathematics (Multidisciplinary Digital Publishing Institute). 2019, 7 (8): 690.

[Mathworld.PentagonalIcositetrahedralGraph-24] 22.0 ^22.1 ^22.2 ^22.3 ^22.4 Weisstein, Eric W. (编). Pentagonal Icositetrahedral Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英えい语）.

[topics-25] Chartrand G., Johns G., Oellermann O.R. On Peripheral Vertices in Graphs. Bodendiek R., Henn R. (编). Topics in Combinatorics and Graph Theory. Physica-Verlag HD. 1990.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

扭棱鑲嵌對稱たいしょう性せい n32 的てき變種へんしゅ： 3.3.3.3.n
對稱たいしょう性せい n32（英えい语：Orbifold notation）	球面きゅうめん鑲嵌（英えい语：List of spherical symmetry groups）				歐おう氏し鑲嵌（英えい语：List_of_planar_symmetry_groups）	緊湊雙そう曲きょく		仿緊雙そう曲きょく
對稱たいしょう性せい n32（英えい语：Orbifold notation）	232	332	432	532	632	732	832	∞32
考こう克かつ斯特記とっき號ごう
扭稜圖ず
頂點ちょうてん圖ず	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7（英えい语：Snub triheptagonal tiling）	3.3.3.3.8（英えい语：Snub trioctagonal tiling）	3.3.3.3.∞（英えい语：Snub triapeirogonal tiling）
扭稜對偶たいぐう
頂點ちょうてん佈局（英えい语：Vertex configuration）	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7（英えい语：Order-7-3 floret pentagonal tiling）	V3.3.3.3.8（英えい语：Order-8-3 floret pentagonal tiling）	V3.3.3.3.∞

扭棱鑲嵌對稱たいしょう性せい 4n2 的てき變種へんしゅ： 3.3.4.3.n
對稱たいしょう性せい 4n2（英えい语：Orbifold notation）	球面きゅうめん鑲嵌（英えい语：List of spherical symmetry groups）		歐おう氏し鑲嵌（英えい语：List_of_planar_symmetry_groups）	緊湊雙そう曲きょく				仿緊雙そう曲きょく
對稱たいしょう性せい 4n2（英えい语：Orbifold notation）	242	342	442	542	642	742	842	∞42
扭稜圖ず
頂點ちょうてん佈局（英えい语：Vertex configuration）	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5（英えい语：Snub tetrapentagonal tiling）	3.3.4.3.6（英えい语：Snub tetrahexagonal tiling）	3.3.4.3.7（英えい语：Snub tetraheptagonal tiling）	3.3.4.3.8（英えい语：Snub tetraoctagonal tiling）	3.3.4.3.∞（英えい语：Snub tetrapeirogonal tiling）
扭稜對偶たいぐう
頂點ちょうてん佈局（英えい语：Vertex configuration）	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

對稱たいしょう性せい（英えい语：List_of_spherical_symmetry_groups）: [4,3], (*432)（英えい语：Octahedral symmetry）								[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)（英えい语：Tetrahedral symmetry）		[3⁺,4] (3*2)（英えい语：pyritohedral symmetry）
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	c{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=					= or	= or	=

對偶たいぐう多面體ためんたい
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V4.6²/6³	V3⁴.4	V3³	V3.6²	V3⁵

性質せいしつ[编辑]

面めん的てき組成そせい[编辑]

體積たいせき與あずか表面積ひょうめんせき[编辑]

正せい交投影とうえい[编辑]

變體へんたい[编辑]

相關そうかん多面體ためんたい及鑲嵌[编辑]

五ご角かく二に十じゅう四よん面體めんてい圖ず[编辑]

性質せいしつ[编辑]

參まいり見み[编辑]

參考さんこう文獻ぶんけん[编辑]

外部がいぶ連結れんけつ[编辑]