 古代攻城用的重力拋石機,利用平衡重鎚的重力势能,將石頭拋向敵城。
古代攻城用的重力拋石機,利用平衡重鎚的重力势能,將石頭拋向敵城。
 亞洲最大的天荒坪抽水蓄能電站將電力用勢能的形式儲存
亞洲最大的天荒坪抽水蓄能電站將電力用勢能的形式儲存
势能[註 1](potential energy,译位能)是储存于一物理系统内的一种能量,是一个用来描述物体在保守力场中做功能力大小的物理量。保守力作功与路径無關,故可定义一个仅与位置有关的函数,使得保守力沿任意路径所做的功,可表达为这两点函数值的差,这个函数便是勢能。
從物理意义上来说,势能表示物體在特定位置上所储存的能量,描述作功能力的大小。在适当的情况下,勢能可以轉化為例如動能、内能等其他能量。
如果分别作用于两个质点上的作用力与反作用力作功与具体路径无关,只取决于相互作用质点初末位置,那么这样的一对力就叫作保守力。不满足这个条件的则称为非保守力。可以证明保守场的几个等价条件[2],于是我们得到保守力的性质有:
- 保守力沿给定两点间作功与路径无关;
- 保守力沿任意环路作功为零;
- 保守力可以表示为一个标量函数的(负)梯度;
推广到多质点体系和连续分布物体,如果一封闭系统中任意两个质点之间的作用力都是保守力,则称该系统为保守体系。保守体系的位形,即在保守体系中各质点的相对位置发生变化时,其间的相互作用力作功,作功之和只与各质点相对位置有关。将保守体系在保守力作用下的这种与相对位置相联系的作功的能力定义为一个函数,称为该保守体系的势能函数或位能函数,简称势能或位能[3]。这样,体系从一种位形变为另一种位形时对外界所作的功等于后者与前者的势能之差,从而赋予了势能函数以直观的物理意义。
除此之外,我们还可以将势能的定义从现在的基础上拓展。比如热学中气体分子间的相互作用势能,它是大量分子势能的和,实际不是用相对位置(位形)来描述的,而是用体积、温度、压强等热学参量。又如,在一些特定的约束条件下,某些平时是非保守力的力也成为了保守力[4],或者几种力的合力恰巧成为了一个保守力。
对于一个理想、完整体系,有拉格朗日方程

其中,T为体系动能,qα为广义坐标的α分量,Qα为广义力合力的α分量,s为广义坐标数。在传统的势能定义下,保守力合力可以写为

其中,V为体系势能。用广义坐标写为

代入拉格朗日方程便可得到

若广义力Qα并不能表示成关于任意函数V的上述函数,却能找到另一个函数U,使得Qα可以表示为

则代入拉格朗日方程仍有

这时U具有与V相似的数学形式,但已经不再与保守力有关。我们把U叫做广义势能[5]。
广义势能最主要的应用在于带电粒子在电磁场中的运动上。带有电荷q,以速度v移動的粒子在电场E和磁场B中受到洛伦兹力

再辅以麦克斯韦方程组,定义電势φ与矢势A,可以得到一个满足上述条件的函数[6]

在下面的介绍中,不经特殊说明,我们只涉及传统意义上的势能,不涉及广义势能。
势能为能量的一种,具有能量量纲,在国际单位制下的单位是焦耳(J),另外在涉及到粒子物理时常用到电子伏特(eV),高斯单位制下为尔格(erg)。势能一般使用“Ep”[3]表示,也常使用“W”[7]“U”和“V”[8]。
势能是一个标量函数,当一个物体与多个物体共有势能或共有多种势能时,这个物体所具有的总势能为所有势能的代数和。
由定义可知,势能取决于两个或多个物体的相对位形,是两个或多个物体所共有的。然而,在两物体A、B组成的保守体系中,如果我们以其中一个物体A作为参考系,则势能仅取决于另一物体B的相对位置。这时,在不引起混淆的情况下,我们常把“A、B具有的势能”称作是“B的势能”。比如,在电场中的电荷具有静电势能,或者是在一个天体附近的另一个天体具有引力势能。除此之外,有时候保守体系中只存在一个物体,势能来自于物体内部各部分间的相对位移,这时候我们也说,势能是这个物体所具有的。比如,弹簧,或者是具有体分布电荷的绝缘体球。
需要注意的是,即使在同一保守力场中的同一处,不同物体的势能也一般不同,比如在重力作用范围内,物体的重力势能不仅取决于其高度,还取决于其质量。
 三峡水力发电站。用大坝将水高高蓄起,然后在大坝处飞泻而下,带动发电机。虽然经过一系列复杂的转换,然而电能的根本来源是水的重力势能。
三峡水力发电站。用大坝将水高高蓄起,然后在大坝处飞泻而下,带动发电机。虽然经过一系列复杂的转换,然而电能的根本来源是水的重力势能。
当物体从高势能处来到低势能处时,该物体势能减少,而保守力向外作等量功使其它某种能量增加。从中我们可以发现,势能可以表示一个物体所储存的能量的多少。如,放在高处的物体相比放在放在低处的物体而言具有更多的重力势能,当它从空中向下坠落的时候,重力势能减少,转化为动能;而当它沿粗糙斜面下滑时,重力势能同时转化为动能和内能。
具有更多势能的物体有能力对外界作出更多的功。[9]故,当物体在保守力的作用下从a处沿任意路径移动到b处时,势能变化量为保守力作功的相反值,即

通常我们并不在意势能的绝对大小,而是关心其变化量,这从势能的定义可以明显看出;实际上,谈一个物体究竟拥有多少绝对势能是没有意义的。不过,有时为了计算或者叙述方便,我们也取一个势能零点O,规定O处势能Ep(O)=0,这样质点在a点的势能大小为

原则上势能零点可任意取,一般依方便而定;如果可能,一般选Fcon=0点为势能零点。[10]
势能为保守力关于位移的积分,相对地,保守力为相应势能函数关于位移的负梯度,即

使用广义坐标描述时,可写为


描述势能随位置变化的图称为势能图。若势能为仅与一个坐标(或广义坐标)有关的函数,这时势能图成为势能曲线,可以在平面直角坐标系上表示出来,这时负梯度退化为负导数,

在下面介绍平衡及各种势能的时候会有势能曲线的范例。
势能Ep与动能Ek之和称为机械能。

外力的功与非保守内力的功之和等于质点系机械能的增量,这就是质点系的功能原理。用数学方式表达出来为

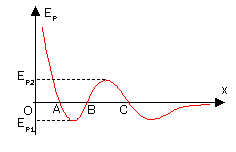 在x方向上运动的一个机械能守恒的粒子,遭遇到势阱与势垒
在x方向上运动的一个机械能守恒的粒子,遭遇到势阱与势垒
其中, 为外力作功,
为外力作功, 为非保守内力作功。若
为非保守内力作功。若 ,
, ,则质点系机械能守恒,这就是机械能守恒定律。这时,质点系与外界无能量交换,内部也无机械能与非机械能的转化,只有动能与势能的相互转换。
,则质点系机械能守恒,这就是机械能守恒定律。这时,质点系与外界无能量交换,内部也无机械能与非机械能的转化,只有动能与势能的相互转换。
在构建理想模型时,机械能守恒定律应用得十分广泛,特别是当一质点处在有心力场时,其机械能守恒;又因为动能Ek>0,在已知总能量的情况下,可以了解到质点理论上的行动范围(满足Ek<E的区域)。
设在x方向上有如图势能曲线,则我们把AB间势能最低处叫作势阱(C右方也有一个势阱),BC间势能最高处叫作势垒,对应的有势阱深度与势垒高度。我们设定粒子机械能守恒,那么:
假設一个粒子从无穷远处靠近,其机械能为E=0,那么在C点处其动能为零,再向左走动能为负,速度将为虚数,经典力学中这是不允许的。因此它最多只能到达C处。随着粒子机械能(即初动能)的增大,其运动范围的左端将会延伸,当其机械能达到或超过Ep2时,它将可以翻过势垒。
再假设一个粒子,初始时在AB间。若它机械能为0,那么它可以在AB间运动,其最大动能为Ek max=Ep1。当其机械能不断增大,达到Ep2时,它将可以翻越势垒,到达B右方空间(当然,其在A左方的空间也会延伸)。
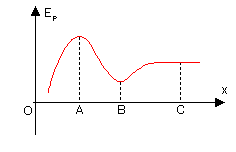 粒子在A点不稳定平衡,在B点稳定平衡,在C点随遇平衡。
粒子在A点不稳定平衡,在B点稳定平衡,在C点随遇平衡。
势能图、势垒等概念是讨论单个质点在保守外场中运动的有力工具,在物理学多个领域中的应用都十分广泛。[11]
物体在势能场中的平衡
[编辑]只受保守力作用的物体,总有向总势能更低处运动的趋势。当物体所处位置不受力作用或合力为零时,即 ,则称物体处于平衡。右图A、B、C三点皆处于平衡。
,则称物体处于平衡。右图A、B、C三点皆处于平衡。
当物体偏离平衡位置时,若受合力背向平衡位置,则物体有离开平衡位置的趋势,则称物体处于不稳定平衡。势能曲线上,不稳定平衡即满足 的点。右图A点处于不稳定平衡。
的点。右图A点处于不稳定平衡。
当物体偏离平衡位置时,若受合力指向平衡位置,则物体有回到平衡位置的趋势,则称物体处于稳定平衡。势能曲线上,稳定平衡即满足 的点。右图B点处于稳定平衡。
的点。右图B点处于稳定平衡。
 马鞍面,即双曲抛物面。从马鞍面原点出发,在x方向上为稳定平衡,在y方向上为不稳定平衡。
马鞍面,即双曲抛物面。从马鞍面原点出发,在x方向上为稳定平衡,在y方向上为不稳定平衡。
当物体在平衡位置附近时合力恒为零,则称物体处于随遇平衡。势能曲线上,随遇平衡即满足 的点。右图C点处于随遇平衡。
的点。右图C点处于随遇平衡。
以上只是一种粗略的分析方法,实际上,在二维或高维空间中情况会更加复杂,比如,在不同的方向上具有不同的平衡种类[12]。一个最简单的例子是,若物体被约束在马鞍形势能曲面上,位于中心时,在x方向上为稳定平衡,在y方向上为不稳定平衡。
在物理中有时会提到势,请不要与势能相混淆。势通常表述为势能与一个物理量的比值,如电势(一个粒子静电势能与其电荷量的比值),引力势(一个物体引力势能与其质量的比值)。一个确定保守力场中,一个物体的势能与该物体有关,但势的分布与该物体无关[13]。
需要与势能区分开的是,物体并不一定总是向势更低的地方运动。一个正电荷会趋向于达到电势更低的地方,但一个负电荷会趋向于达到电势更高的地方,但那里都分别是它们势能更低处。
势也包括一些势能所不包括的内容,如磁矢势。
下面介绍几种常见势能。
在下面的介绍中,我们常考虑一个两质点组成的保守体系,两质点间受且仅受相应的一种保守力。两质点的势能是一种最简单、最理想的模型,然而也是实际模型的基础。实际的问题理论上都可以由两质点势能的函数加以积分得到。
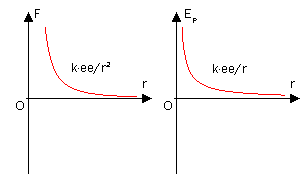
 引力和引力势能随r变化的示意图
引力和引力势能随r变化的示意图
- 注意:在臺湾将万有引力统称为“重力”,然而在大陆地区将万有引力称作“引力”,而将“重力”作为万有引力的一种特殊简化情形。这里为了分别介绍两种情况,不致混淆,暂采用大陆命名方法。
根据牛顿万有引力定律,对于两质点m0、m,质点m受到的万有引力为

其中G是万有引力常数,m0、m是两质点的质量,r0、r分别为两质点的位置矢量。引力场中的物体会具有引力势能。对于两个质点,定义无穷远处为势能零点,则质点m在r处的引力势能为

在实际问题中,对于已知引力势分布φ=φ(r),质点m在r处的引力势能为

 重力和重力势能随h变化的示意图
重力和重力势能随h变化的示意图
重力势能是引力势能在一种特殊情况下的简化形式。可以证明[14],对一球对称分布物体在其外一质点产生的引力,上面两质点间的作用力公式仍适用,其中m0为该物体总质量,r0为其球心位矢。当 |r-r0| 在不太大范围内变动时,对作用力公式取零级近似,作用力不变,则引力退化为重力。[15]由此可见,重力的近似要求很严格。然而由于在日常生活中这个条件很容易满足,而且极简便,符合人们的日常生活经验,故仍有研究价值,单列一项。
在这种情况下,重力大致[16]只与星体性质与物体质量有关,而与位置无关,方向铅直向下[17]。将重力加速度定为常数g,则物体重力大小为

其中m为物体质量,g为重力加速度常数。则物体在h处的重力势能为
 。
。
其中h为物体的高度。
重力势能并没有严格的势能零点定义,完全依计算方便而定,不过比较常用的是以地面或桌面为势能零点。
在地球上g的值约为9.8 ms-2,在不同地区稍有不同。这个值已经包括了和地球自转所需的向心力造成的差别。一般计算中g可近似的取作标准重力加速度,即g=gn=9.80665 ms-2 [18]。
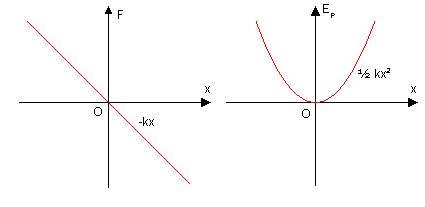 弹簧的弹力和弹性势能随x变化的示意图
弹簧的弹力和弹性势能随x变化的示意图
弹簧、钢片、金属丝等满足胡克定律的物体,在弹性限度内应力与应变成正比。下面以弹簧为例。在弹性限度内,弹簧弹力与长度变化量的关系为

其中,k为弹簧弹性系数,x为弹簧长度变化(即固定一端时另一端相对平衡位置的位移)。则其弹性势能为

弹性势能为对应物体自身所拥有,一般选择弹簧原长时(x=0)为势能零点。
 一个质子受到的另一个质子的静电力和电势能随r变化的示意图
一个质子受到的另一个质子的静电力和电势能随r变化的示意图
在靜電學裏,根据库伦定律,对于两静止点电荷q、q0,点电荷q受到的静电力为

其中ε0是电常数,r0、r分别为两点电荷的位置矢量。静电场中的点电荷会具有电势能。对于两个点电荷,定义无穷远处为势能零点,则点电荷q在r处的电势能为
 。
。
在实际问题中,对于已知电势分布φ=φ(r),点电荷q在r处的电势能为

电势能基于静电场的定律库仑定律。在变化电磁场中,粒子受力不再为保守力,不再能单独用一个标量势函数描述,需要使用标势φ与矢势A共同描述[19]。
 兰纳-琼斯势中,分子间作用力和分子势能随r变化的示意图
兰纳-琼斯势中,分子间作用力和分子势能随r变化的示意图
分子力实际上来源于多个方面,精确的计算与各分子内部结构有很大关系,会变得十分复杂。对于无极性分子,两分子间作用力可近似用以下半经验公式表示:[20]

其中正表示排斥力,负表示牽引力;r为两分子间距,λ、μ、s、t为常数,随两分子不同而不同,且s>t。这种力的特点是
- 在某一个值r0以内,分子里表现为排斥力并且随r减小而急剧上升;
- 在r0以外表现为牽引力,分子力逐渐增大,到某最大值后减小;
- 力程短,在r约为r0十倍时已几乎为零。
由此,对无极性分子间的相互作用势能有以下几个常用曲线。一个典型且常用的模型是兰纳-琼斯势[21],该势能仅与两分子间距有关,具有球对称性,其函数解析式为
 苏则朗势。
苏则朗势。
![{\displaystyle E_{p}(r)=E_{p0}\left[\left({\frac {r_{0}}{r}}\right)^{12}-2\left({\frac {r_{0}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bf945a259e8680ea68cf82789f29a8d8a92d77)
其中,r为两分子距离,Ep0为分子势能的势阱(势能最低处的势能绝对值),r0为势阱处两分子间距。Ep0与r0需要对于具体分子通过实验确定。
对兰纳-琼斯势在排斥力部分简化,成为苏则朗势(Sutherland potential),即

其中E、d为常数,因分子而异。满足苏则朗势的气体称为范德瓦尔斯气体,分子力又称作范德瓦尔斯力,满足范德瓦尔斯方程[22]。
 刚球势。
刚球势。
对苏则朗势在引力部分再次简化,成为刚球势,即

d=0时,分子势能完全忽略,变为质点势,这时气体称作理想气体[23],满足理想气体状态方程。
- ^ 位能. 术语在线. 全国科学技术名词审定委员会. (简体中文)
- ^ 文丽,吴良大.《高等数学·第二册:物理类(修订版)》,P354。
- ^ 3.0 3.1 郑永令,贾起民,方小敏.《力学(第二版)》,P157。
- ^ 见磁标势。
- ^ 以上证明见金尚年,马永利.《理论力学(第二版)》,P48。
- ^ 金尚年,马永利.《理论力学(第二版)》,P49。
- ^ 贾瑞皋,薛庆忠.《电磁学(第二版)》,P46。
- ^ 金尚年,马永利.《理论力学(第二版)》,P18。
- ^ 用非保守力对物体做功可以增加物体的总势能,而若用保守力对物体做功,则物体一种势能增加而另一种势能减少,总势能不变。
- ^ 舒幼生.《力学(物理类)》,P86。
- ^ 赵凯华,罗蔚茵.《力学(第二版)》,P115。
- ^ 郑永令,贾起民,方小敏.《力学(第二版)》,P163。
- ^ 准确地说,当该物体对周围环境影响足够小时。比如电场中一个电量很小的点电荷(被称作试探电荷),当电量较大时会严重影响到周围物体上的电荷分布从而影响到势分布。关于试探电荷见电场#电场强度或贾起民,郑永令,陈暨耀.《电磁学(第二版)》,P13。
- ^ 赵凯华,罗蔚茵.《力学(第二版)》,P337。
- ^ 实际对于重力的定义略稍复杂,参见万有引力#两者的微妙差别。
- ^ 对于计入离心力的重力定义,重力还与物体所处经纬度有关。参见万有引力#两者的微妙差别。另外,由于地球实际分布非完全球对称及地球实际略椭,也导致重力在各地有微小差异。
- ^ 由于离心力的原因,在一般情况下“铅直向下”方向并不指向地心,然而重力方向仍然是与铅直向下方向完全一致的。
- ^ 存档副本. [2010-01-12]. (原始内容存档于2009-02-24).
- ^ 使用拉格朗日方程时也可以使用广义势能U=q(φ+v·A)描述,见#广义势能
- ^ 包科达.《热物理学基础》,P44。
- ^ 包科达.《热物理学基础》,P45。
- ^ 包科达.《热物理学基础》,P58。
- ^ 包科达.《热物理学基础》,P48。
- 赵凯华,罗蔚茵. 《新概念物理教程·力学(第二版)》. 北京: 高等教育出版社. 2004. ISBN 7-04-015201-0.
- 文丽,吴良大. 《高等数学·第二册:物理类(修订版)》. 北京: 北京大学出版社. 2002. ISBN 7-301-07543-X.
- 贾起民,郑永令,陈暨耀. 《电磁学(第二版)》. 北京: 高等教育出版社. 2003. ISBN 7-04-008603-4.
|
|---|
| 表述形式 | |
|---|
| 基础概念 | |
|---|
| 重要理论 | |
|---|
| 应用 | |
|---|
| 科学史 | |
|---|
| 分支 | |
|---|

















































![{\displaystyle E_{p}(r)=E_{p0}\left[\left({\frac {r_{0}}{r}}\right)^{12}-2\left({\frac {r_{0}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bf945a259e8680ea68cf82789f29a8d8a92d77)

