在 ざい 巨 きょ 著 ちょ 自然 しぜん 哲學 てつがく 的 てき 數學 すうがく 原理 げんり 年 ねん 版本 はんぽん 裏 うら 拉 ひしげ 丁 ちょう 文 あや 撰 せん 寫 うつし 的 てき 牛 うし 頓 ひたぶる 第 だい 一 いち 運動 うんどう 定律 ていりつ 牛 うし 頓 ひたぶる 第 だい 二 に 運動 うんどう 定律 ていりつ 牛 うし 一 いち 定律 ていりつ [ 1] Newton's first law of motion ,台湾 たいわん 牛 うし 頓 ひたぶる 第 だい 一 いち 運動 うんどう 定律 ていりつ 又 また 称 たたえ 惯性定律 ていりつ ”(law of inertia )[ 1] 定律 ていりつ 表明 ひょうめい 假 かり 若 わか 施 ほどこせ 加 か 物體 ぶったい 的 てき 外力 がいりょく 為 ため 零 れい 則 のり 物體 ぶったい 的 てき 運動 うんどう 速度 そくど 不變 ふへん [ 2] 根據 こんきょ 定律 ていりつ 假設 かせつ 沒 ぼつ 有 ゆう 任 にん 何 なん 外力 がいりょく 施 ほどこせ 加 か 或 ある 所 ところ 施 ほどこせ 加 か 的 てき 外力 がいりょく 之 の 和 わ 則 のり 中 ちゅう 物体 ぶったい 保持 ほじ 匀速直 ちょく 状 じょう 静止 せいし 物体 ぶったい 保持 ほじ 静止 せいし 状 じょう 物體 ぶったい 所 しょ 呈 てい 現出 げんしゅつ 的 てき 維持 いじ 運動 うんどう 狀態 じょうたい 不變 ふへん 的 てき 性質 せいしつ 稱 しょう 為 ため 慣性 かんせい 牛 うし 一 いち 定律 ていりつ 又 また 稱 しょう 為 ため 定律 ていりつ 只 ただ 成立 せいりつ 慣性 かんせい 參考 さんこう 系 けい 又 また 稱 たたえ 為 ため 牛 うし 頓 ひたぶる 參考 さんこう 系 けい [ 3]
1687年 ねん 英國 えいこく 物理 ぶつり 泰斗 たいと 艾 もぐさ 牛 うし 在 ざい 巨 きょ 著 ちょ 自然 しぜん 哲學 てつがく 的 てき 數學 すうがく 原理 げんり 裏 うら 提出 ていしゅつ 了 りょう 牛 うし 頓 ひたぶる 運動 うんどう 定律 ていりつ 中有 ちゅうう 三 さん 條 じょう 定律 ていりつ 分別 ふんべつ 為 ため 牛 うし 頓 ひたぶる 第 だい 一 いち 運動 うんどう 定律 ていりつ 牛 うし 頓 ひたぶる 第 だい 二 に 運動 うんどう 定律 ていりつ 與 あずか 牛 うし 頓 ひたぶる 第 だい 三 さん 運動 うんどう 定律 ていりつ [ 4]
在 ざい 歷史 れきし 上 じょう 第 だい 在 ざい 所有 しょゆう 現代 げんだい 物理 ぶつり 學 がく 裡 うら 不可 ふか 或 ある 缺 かけ 的 てき 基礎 きそ 然 しか 教科書 きょうかしょ 都 と 沒 ぼつ 能 のう 合 あい 明確 めいかく 表 ひょう 述 じゅつ 出 で 定律 ていりつ 物理 ぶつり 學者 がくしゃ 約 やく 瑞 みず 格 かく 登 とう 認 みとめ 為 ため 定律 ていりつ 是 ぜ 惡夢 あくむ 但 ただし 譽 ほまれ 定律 ていりつ 是 ぜ 難 なん 形容 けいよう 的 てき 奧 おく 妙 みょう [ 5] [ 註 1] [ 註 2]
牛 うし 一 いち 定律 ていりつ 表明 ひょうめい 假 かり 若 わか 施 ほどこせ 加 か 物體 ぶったい 的 てき 外力 がいりょく 為 ため 零 れい 則 のり 物體 ぶったい 的 てき 運動 うんどう 速度 そくど 不變 ふへん 方程式 ほうていしき 表 ひょう 達 たち [ 2]
∑
i
F
i
=
0
⇒
d
v
d
t
=
0
{\displaystyle \sum _{i}\mathbf {F} _{i}=0\Rightarrow {\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}=0}
其中,
F
i
{\displaystyle \mathbf {F} _{i}}
是 ぜ 第 だい
i
{\displaystyle i}
個 こ 外力 がいりょく
v
{\displaystyle \mathbf {v} }
是 ぜ 速度 そくど
t
{\displaystyle t}
是 ぜ 時間 じかん
從 したがえ 第 だい
靜止 せいし 的 てき 物體 ぶったい 會 かい 保持 ほじ 靜止 せいし 狀態 じょうたい 除 じょ 非 ひ 有 ゆう 外力 がいりょく 施 ほどこせ 加 か 物體 ぶったい 運動 うんどう 中 ちゅう 的 てき 物體 ぶったい 不 ふ 會 かい 改變 かいへん 運動 うんどう 速度 そくど 除 じょ 非 ひ 有 ゆう 外力 がいりょく 施 ほどこせ 加 か 物體 ぶったい 注意 ちゅうい 到 いた 速度 そくど 是 ぜ 向 むこう 量 りょう 物體 ぶったい 運動 うんどう 速度 そくど 的 てき 大小 だいしょう 與 あずか 方向 ほうこう 都 と 不 ふ 會 かい 改變 かいへん 根據 こんきょ 第 だい 一 いち 定律 ていりつ 從 したがえ 測量 そくりょう 物體 ぶったい 的 てき 運動 うんどう 速度 そくど 是 ぜ 否 ひ 改變 かいへん 可 か 判斷 はんだん 是 ぜ 否 いや 有 ゆう 外力 がいりょく 作用 さよう 體 たい 但 ただし 是 ぜ 第 だい 有給 ゆうきゅう 出 で 力 りょく 的 てき 來 らい 源 げん 是 ぜ 將 はた 物體 ぶったい 運動 うんどう 速度 そくど 的 てき 改變 かいへん 歸 き 因 いん 為 ため 外力 がいりょく 的 てき 施 ほどこせ 加 か 體 たい [ 8] 從 したがえ 一 いち 個 こ 角度 かくど 來 らい 看 み 只 ただ 有 ゆう 因 いん 為 ため 外力 がいりょく 的 てき 施 ほどこせ 加 か 物體 ぶったい 才 ざい 會 かい 改變 かいへん 物體 ぶったい 的 てき 運動 うんどう 否 いや 則 のり 物體 ぶったい 的 てき 運動會 うんどうかい 永遠 えいえん 保持 ほじ 不變 ふへん 味 あじ 著 ちょ 物體 ぶったい 擁 よう 有 ゆう 某 ぼう 種 しゅ 懶 ものぐさ 改變 かいへん 運動 うんどう 狀態 じょうたい 的 てき 性質 せいしつ 稱 しょう 為 ため 物體 ぶったい 的 てき 慣性 かんせい [ 9]
第 だい 一 いち 定律 ていりつ 是 ぜ 物理 ぶつり 定律 ていりつ 因 いん 具有 ぐゆう 可 か 證 あかし 偽 にせ 性 せい 即 そく 實驗 じっけん 可 か 對 たい 第 だい 一 いち 定律 ていりつ 是 ぜ 否 ひ 正確 せいかく 在 ざい 實驗 じっけん 時 じ 必須 ひっす 測量 そくりょう 物體 ぶったい 的 てき 運動 うんどう 速度 そくど 但 ただし 參考 さんこう 系 けい 的 てき 設定 せってい 因 よし 可 か 詳細 しょうさい 地 ち 將 はた 第 だい 一 いち 定律 ていりつ 表明 ひょうめい 為 ため [ 10]
採用 さいよう 某 ぼう 種 たね 參考 さんこう 系 けい 來 らい 測量 そくりょう 假 かり 若 わか 施 ほどこせ 加 か 一 いち 個 こ 物體 ぶったい 的 てき 外力 がいりょく 為 ため 零 れい 則 のり 物體 ぶったい 的 てき 運動 うんどう 速度 そくど 不變 ふへん
儘管在 ざい 自然 しぜん 哲學 てつがく 的 てき 數學 すうがく 原理 げんり 裏 うら 沒 ぼつ 有明 ありあけ 確 かく 地 ち 指 ゆび 明 あかり 應 おう 樣 さま 詮 かい 釋 しゃく 作用 さよう 力 りょく 從 したがえ 第 だい 牛 うし 頓 ひたすら 認 みとめ 為 ため 零 れい 作用 さよう 力 りょく 案 あん 例 れい 可 か 容易 ようい 地 ち 被 ひ 辨 べん 認 みとめ 出來 でき 例 れい 能 のう 性 せい 參考 さんこう 系 けい 給 きゅう 出 で 定義 ていぎ 假 かり 若 わか 從 したがえ 一 いち 個 こ 參考 さんこう 系 けい 觀測 かんそく 不 ふ 的 てき 物體 ぶったい 的 てき 運動 うんどう 速度 そくど 不變 ふへん 則 のり 參考 さんこう 系 けい 是 ぜ 慣性 かんせい 參考 さんこう 系 けい 在 ざい 宇宙 うちゅう 中 ちゅう 存在 そんざい 著 ちょ 無數 むすう 可能 かのう 的 てき 參考 さんこう 系 けい 在 ざい 參考 さんこう 系 けい 中 ちゅう 滿足 まんぞく 第 だい 慣性 かんせい 參考 さんこう 系 けい 滿足 まんぞく 第 だい 非 ひ 慣性 かんせい 參考 さんこう 系 けい 因 よし 第 だい 從 したがえ 實驗 じっけん 觀察 かんさつ 物體 ぶったい 的 てき 運動 うんどう 行為 こうい 別 べつ 出 で 是 ぜ 慣性 かんせい 參考 さんこう 系 けい 不 ふ 是 ぜ 慣性 かんせい 參考 さんこう 系 けい [ 11] 至 いたり 今 いま 為 ため 止 やめ 多 た 個 こ 位 い 地球 ちきゅう 表面 ひょうめん 固定 こてい 地點 ちてん 的 てき 實驗 じっけん 室 しつ 所 しょ 完成 かんせい 的 てき 關 せき 經典 きょうてん 力學 りきがく 的 てき 實驗 じっけん 建議 けんぎ 實驗 じっけん 室 しつ 適合 てきごう 實現 じつげん 慣性 かんせい 參考 さんこう 系 けい 對 たい 合 あい 適 てき 的 てき 實驗 じっけん 則 のり 必須 ひっす 設計 せっけい 與 あずか 建造 けんぞう 更 さら 為 ため 精緻 せいち 的 てき 實驗 じっけん 室 しつ [ 10]
在 ざい 實驗 じっけん 核 かく 對 たい 第 だい 一 いち 定律 ていりつ 時 じ 還 かえ 必須 ひっす 測量 そくりょう 是 ぜ 否 いや 有 ゆう 外力 がいりょく 施 ほどこせ 加 か 體 たい 味 あじ 著 ちょ 必須 ひっす 對 たい 給 きゅう 出 で 嚴格 げんかく 定義 ていぎ 牛 うし 頓 ひたぶる 在 ざい 自然 しぜん 哲學 てつがく 的 てき 數學 すうがく 原理 げんり 裏 うら 提出 ていしゅつ 第 だい 一 いち 定律 ていりつ 後 ご 又 また 列 れつ 分別 ふんべつ 為 ため 空氣 くうき 與 あずか 重力 じゅうりょく 的 てき 施 ほどこせ 加 か 拋體 、空氣 くうき 與 あずか 的 てき 施 ほどこせ 加 か 螺 にし 行 くだり 星 ぼし 與 あずか 彗星 すいせい 的 てき 移動 いどう 自由 じゆう 空間 くうかん 牛 うし 頓 ひたすら 還 かえ 給 きゅう 出 で 了 りょう 三 さん 種 しゅ 外力 がいりょく 分別 ふんべつ 為 ため 衝擊 しょうげき 力 りょく 壓力 あつりょく 與 あずか 離 はなれ 心力 しんりょく 但 ただし 是 ぜ 他 た 並 なみ 沒 ぼつ 有 ゆう 對 たい 給 きゅう 出 で 嚴格 げんかく 定義 ていぎ [ 4] [ 註 3]
懸 かか 掛 かけ 條 じょう 特定 とくてい 彈 だん 一 いち 個 こ 物體 ぶったい 正 せい 好 こう 能 のう 條 じょう 特定 とくてい 彈 だん 延伸 えんしん 特定 とくてい 距離 きょり 則 のり 物體 ぶったい 的 てき 重量 じゅうりょう
W
{\displaystyle \mathbf {W} }
等 とう 兩個 りゃんこ 標準 ひょうじゅん 單位 たんい 力 りょく
F
0
{\displaystyle \mathbf {F} _{0}}
[ 14] 使用 しよう 操作 そうさ 定義 ていぎ 的 てき 方法 ほうほう 可 か 給 きゅう 出 で 嚴格 げんかく 定義 ていぎ 例 れい 兩個 りゃんこ 同樣 どうよう 的 てき 彈 だん 假 かり 若 わか 被 ひ 壓縮 あっしゅく 同樣 どうよう 的 てき 距離 きょり 則 のり 各自 かくじ 產 さん 生 せい 的 てき 彈力 だんりょく 一種 いっしゅ 物理 ぶつり 現象 げんしょう 必定 ひつじょう 相等 そうとう 將 はた 兩個 りゃんこ 彈 だん 並 なみ 聯 れん 則 のり 可 か 生 せい 兩 りょう 倍 ばい 的 てき 彈力 だんりょく 將 しょう 使 つかい 彈力 だんりょく 的 てき 作用 さよう 方向 ほうこう 相反 あいはん 則 のり 作用 さよう 物體 ぶったい 的 てき 淨 きよし 力 りょく 為 ため 零 れい 為 ため 了 りょう 對 たい 力 りょく 給 きゅう 出 で 定量 ていりょう 設定 せってい 標準 ひょうじゅん 單位 たんい 力 りょく 為 ため 某 ぼう 特定 とくてい 彈 だん 壓縮 あっしゅく 特定 とくてい 距離 きょり 所產 しょさん 生 せい 的 てき 彈力 だんりょく 任意 にんい 數量 すうりょう 的 てき 標準 ひょうじゅん 單位 たんい 力 りょく 都 と 可 か 幾 いく 個 こ 彈 だん 組成 そせい 的 てき 系統 けいとう 來 らい 實現 じつげん 彈 たま 系統 けいとう 可 か 來 らい 測量 そくりょう 實驗 じっけん 對 たい 意力 いりょく 比較 ひかく 給 きゅう 出 で 測量 そくりょう [ 11] [ 15]
另外還 かえ 有 ゆう 古 こ 夫 おっと 基 もと 夫 おっと 最 さい 先 さき 給 きゅう 出 で 後來 こうらい 又 また 獲得 かくとく 恩 おん 馬 ば 海 うみ 因 いん 里 ざと 希 まれ 等 ひとし 人的 じんてき 支持 しじ 繪 え 景 けい 第 だい [ 註 4] 即 そく 將 しょう 力 りょく 定義 ていぎ 為 ため 質量 しつりょう 與 あずか 加速度 かそくど 的 てき 乘 じょう 積 せき [ 註 5] 入力 にゅうりょく 的 てき 概念 がいねん 手 しゅ 的 てき 任務 にんむ 假 かり 若 わか 採用 さいよう 繪 え 景 けい 則 のり 第 だい [ 6] 頓 ひたぶる 並 なみ 沒 ぼつ 有 ゆう 發現 はつげん 力 りょく 是 ぜ 質量 しつりょう 與 あずか 加速度 かそくど 的 てき 乘 じょう 積 せき 因 いん 為 ため 是 ぜ 一 いち 個 こ 定義 ていぎ 牛 うし 頓 ひたぶる 發現 はつげん 的 てき 是 ぜ 物理 ぶつり 定律 ていりつ 比較 ひかく 容易 ようい 用 よう 力 りょく 的 てき 概念 がいねん 來 らい 表 ひょう 達 たち [ 11]
這種繪 え 景 けい 會 かい 導 しるべ 後 ご 果 はて 是 ぜ 整 せい 個 こ 經典 きょうてん 力 りょく 學會 がっかい 變成 へんせい 一 いち 種 しゅ 公理 こうり 化 か 理論 りろん 所有 しょゆう 結論 けつろん 都 と 是 ぜ 源 げん 自 じ 個 こ 定義 ていぎ 是 ぜ 源 げん 自 じ 為 ため 物理 ぶつり 學者 がくしゃ 青 あお 從 したがえ 實驗 じっけん 總 そう 結 ゆい 出 で 的 てき 自然 しぜん 定律 ていりつ 假 かり 若 わか 要 よう 將 しょう 實際 じっさい 物理 ぶつり 理化 りか 理論 りろん 則 のり 必須 ひっす 檢 けん 試 ためし 對 たい 的 てき 定義 ていぎ 所 しょ 導出 どうしゅつ 的 てき 結果 けっか 是 ぜ 否 ひ 符合 ふごう 實際 じっさい 物理 ぶつり 只 ただ 有 ゆう 符合 ふごう 實際 じっさい 物理 ぶつり 才 ざい 可 か 被 ひ 採納 さいのう 換 かわ 句 く 話 はなし 說 せつ 從 したがえ 對 たい 的 てき 定義 ていぎ 所 しょ 演繹 えんえき 出 で 的 てき 規則 きそく 結果 けっか 必須 ひっす 符合 ふごう 實驗 じっけん 的 てき 檢 けん 試 こころみ 否 いや 則 のり 不能 ふのう 被 ひ 採納 さいのう [ 11]
只 ただ 有 ゆう 從 したがえ 某 ぼう 種 たね 特定 とくてい 的 てき 參考 さんこう 系 けい 觀測 かんそく 才 さい 可 か 牛 うし 頓 ひたぶる 定律 ていりつ 與 あずか 實際 じっさい 物理 ぶつり 接 せっ 特定 とくてい 的 てき 參考 さんこう 系 けい 慣性 かんせい 參考 さんこう 系 けい 通過 つうか 實驗 じっけん 可 か 無限 むげん 數量 すうりょう 的 てき 慣性 かんせい 參考 さんこう 系 けい 從 したがえ 任 にん 何 なん 種 しゅ 參考 さんこう 系 けい 觀測 かんそく 都 と 無法 むほう 達成 たっせい 接 せっ 目標 もくひょう 更 さら 具體 ぐたい 只 ただ 有 ゆう 從 したがえ 慣性 かんせい 參考 さんこう 系 けい 才 ざい 可 か 觀測 かんそく 到 いた 不 ふ 物体 ぶったい 的 てき 運動 うんどう 速度 そくど 不變 ふへん [ 11]
阿 おもね 爾 しか 伯 はく 特 とく 愛 あい 因 いん 的 てき 等 とう 效 こう 原理 げんり 指出 さしで 對 たい 一 いち 位 い 處 しょ 引力 いんりょく 場 じょう 的 てき 觀察 かんさつ 者 しゃ 呈 てい 靜止 せいし 狀態 じょうたい 與 あずか 假 かり 若 わか 位 い 觀察 かんさつ 者 しゃ 感 かん 的 てき 力 りょく 相等 そうとう 則 のり 他 た 無法 むほう 分 ぶん 辨 べん 到底 とうてい 感受 かんじゅ 到 いた 的 てき 是 ぜ 引力 いんりょく 還 かえ 是 ぜ 因 いん 加速度 かそくど 生 せい 的 てき 慣性 かんせい 力 りょく 注意 ちゅうい 到 いた 慣性 かんせい 力 りょく 的 てき 方向 ほうこう 與 あずか 加速度 かそくど 的 てき 方向 ほうこう 相反 あいはん 慣性 かんせい 力 りょく 抗拒 こうきょ 加速度 かそくど 運動 うんどう 任 にん 何處 どこ 力 りょく 場 じょう 的 てき 自由 じゆう 落體 らくたい 都 と 不 ふ 會 かい 感 かん 引力 いんりょく 因 いん 為 ため 引力 いんりょく 已 やめ 與 あずか 自由 じゆう 的 てき 加速度 かそくど 運動 うんどう 所 しょ 出現 しゅつげん 的 てき 慣性 かんせい 力 りょく 相互 そうご 因 いん 假設 かせつ 從 したがえ 某 ぼう 個 こ 參考 さんこう 系 けい 觀 かん 自由 じゆう 落體 らくたい 呈 てい 靜止 せいし 狀態 じょうたい 或 ある 或 ある 直線 ちょくせん 運動 うんどう 則 のり 參考 さんこう 系 けい 滿足 まんぞく 第 だい 一 いち 定律 ていりつ 參考 さんこう 系 けい 是 ぜ 慣性 かんせい 參考 さんこう 系 けい 由 よし 採用 さいよう 一 いち 種 しゅ 新 しん 的 てき 觀點 かんてん 即 そく 與 あずか 處 しょ 力 りょく 場 じょう 的 てき 自由 じゆう 落體 らくたい 呈 てい 靜止 せいし 狀態 じょうたい 或 ある 直線 ちょくせん 運動 うんどう 的 てき 參考 さんこう 系 けい 為 ため 慣性 かんせい 參考 さんこう 系 けい [ 11] [ 17]
亞 あ 里 さと 德 とく 認 みとめ 為 ため 在 ざい 宇宙 うちゅう 裏 うら 所有 しょゆう 物體 ぶったい 都 と 有 ゆう 自然 しぜん 位置 いち 處 しょ 美 び 狀態 じょうたい 的 てき 位置 いち 物體 ぶったい 會 かい 固定 こてい 不動 ふどう 地 ち 處 しょ 自然 しぜん 位置 いち 被 ひ 移 うつり 離 はなれ 自然 しぜん 位置 いち 的 てき 物體 ぶったい 會 かい 傾向 けいこう 回 かい 自然 しぜん 位置 いち 因 いん 為 ため 物體 ぶったい 傾向 けいこう 美 び 狀態 じょうたい 的 てき 位置 いち 因 よし 像 ぞう 石頭 いしあたま 像 ぞう 煙 けむり 灰 はい 亞 あ 里 さと 德 とく 仔細 しさい 地區 ちく 分 ぶん 了 りょう 兩 りょう 種 たね 運動 うんどう 自然 しぜん 運動 うんどう 與 あずか 運動 うんどう 重 じゅう 物體 ぶったい 的 てき 自由 じゆう 墜落 ついらく 是 ぜ 一 いち 種 しゅ 自然 しぜん 運動 うんどう 發射 はっしゃ 體 たい 的 てき 運動 うんどう 則 そく 是非 ぜひ 自然 しぜん 運動 うんどう 處 ところ 自然 しぜん 位置 いち 的 てき 物體 ぶったい 傾向 けいこう 固定 こてい 不動 ふどう 只 ただ 有 ゆう 施 ほどこせ 加 か 力 りょく 才能 さいのう 將 はた 物體 ぶったい 移 うつり 離 はなれ 自然 しぜん 位置 いち 所有 しょゆう 運動 うんどう 都 と 不 ふ 具有 ぐゆう 永久 えいきゅう 性 せい 遲 おそ 早 はや 會 かい 終止 しゅうし 結束 けっそく 為 ため 了 りょう 維持 いじ 運動 うんどう 必需 ひつじゅ 繼續 けいぞく 地 ち 施 ほどこせ 加 か 力 りょく 體 たい 使 つかい 離 はなれ 自然 しぜん 位置 いち [ 18] 不 ふ 處 しょ 自然 しぜん 位置 いち 的 てき 任意 にんい 物體 ぶったい 在 ざい 被 ひ 釋放 しゃくほう 後 ご 會 かい 地 ち 達 たち 到 いた 最終 さいしゅう 速度 そくど 然 しか 後 こう 維持 いじ 速度 そくど 直 ちょく 到 いた 移動 いどう 至 いたり 自然 しぜん 位置 いち [ 19]
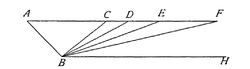
伽 とぎ 利 り 略 りゃく 用 よう 來 らい 檢 けん 驗 けん 慣性 かんせい 定律 ていりつ 的 てき 斜面 しゃめん 實驗 じっけん 伽 とぎ 利 り 略 りゃく 伽 とぎ 利 り 的 てき 想 そう 法大 ほうだい 不 ふ 相 あい 同 どう 伽 とぎ 利 り 略 りゃく 提出 ていしゅつ 的 てき 慣性 かんせい 定律 ていりつ 表明 ひょうめい 只 ただ 有 ゆう 施 ほどこせ 加 か 外力 がいりょく 才能 さいのう 改變 かいへん 物體 ぶったい 速度 そくど 維持 いじ 物體 ぶったい 速度 そくど 不變 ふへん 不 ふ 需要 じゅよう 任 にん 何 なん 外力 がいりょく 為 ため 了 りょう 證 しょう 實 じつ 他 た 的 てき 主張 しゅちょう 是正 ぜせい 確 かく 的 てき 伽 とぎ 利 り 略 りゃく 一 いち 個 こ 思想 しそう 實驗 じっけん 圖 ず 所 しょ 示 しめせ 讓 ゆずる 静止 せいし 的 てき 圓 えん 球 だま 從 したがえ 點 てん 滾 たぎ 下 した 斜面 しゃめん 滾 たぎ 到 いた 最 さい 底 そこ 端 はし 後 ご 圓 えん 球 だま 又 また 會 かい 滾 たぎ 上 うわ 斜面 しゃめん 假設 かせつ 兩 りょう 塊 かたまり 斜面 しゃめん 都 と 非常 ひじょう 的 てき 平滑 へいかつ 摩擦 まさつ 係數 けいすう 爲 ため 零 れい 無 む 空氣 くうき 則 のり 圓 えん 球 だま 會 かい 滾 たぎ 到 いた 與 あずか 點 てん 同 どう 高度 こうど 的 てき 點 てん 對 たい 面 めん 或 ある 圓 えん 球 だま 的 てき 滾 たぎ 動 どう 距離 きょり 會 かい 變 へん 得 とく 越來 ごえく 越 えつ 長 ちょう 圓 えん 球 だま 同樣 どうよう 地 ち 會 かい 滾 たぎ 到 いた 與 あずか 點 てん 同 どう 高度 こうど 的 てき 位置 いち 假設 かせつ 斜面 しゃめん 是 ぜ 水平面 すいへいめん 則 のり 球 だま 永遠 えいえん 不能 ふのう 滾 たぎ 到 いた 先 せん 前 まえ 的 てき 高度 こうど 因 いん 不 ふ 停 とま 地 ち 呈 てい 直線 ちょくせん 運動 うんどう 伽 とぎ 利 り 略 りゃく 總 そう 結 ゆい 運動 うんどう 中 ちゅう 的 てき 物體 ぶったい 會 かい 持續 じぞく 地 ち 速 そく 直線 ちょくせん 運動 うんどう 假 かり 若 わか 不 ふ 任 にん 何 なん [ 20] 伽 とぎ 利 り 略 りゃく 的 てき 慣性 かんせい 定律 ていりつ 對 たい 力學 りきがく 的 てき 基礎 きそ 重大 じゅうだい 貢獻 こうけん 並 なみ 徹底 てってい 地 ち 了 りょう 多 た 年來 ねんらい 學者 がくしゃ 亞 あ 里 さと 德 とく 理論 りろん 因 いん 使 し 十 じゅう 但 ただし 他 た 並 なみ 沒 ぼつ 有 ゆう 建 けん 一 いち 個 こ 新 しん 的 てき 替 がえ 代理 だいり 論 ろん 有 ゆう 待 まち 後來 こうらい 牛 うし 頓 とみ 的 てき 貢獻 こうけん [ 21]
勒内·笛 ふえ 在 ざい 年 ねん 著作 ちょさく 哲學 てつがく 原理 げんり 裏 うら 提出 ていしゅつ 了 りょう 三 さん 條 じょう 自然 しぜん 定律 ていりつ 第 だい 一 いち 條 じょう 自然 しぜん 定律 ていりつ 表明 ひょうめい 假 かり 若 わか 不 ふ 將 しょう 影響 えいきょう 納入 のうにゅう 考量 こうりょう 則 のり 每 ごと 個物 こぶつ 體 たい 永遠 えいえん 會 かい 處 しょ 同樣 どうよう 的 てき 狀態 じょうたい 假 かり 若 わか 處 しょ 移動 いどう 狀態 じょうたい 則 のり 永久 えいきゅう 持續 じぞく 的 てき 移動 いどう 第 だい 二 に 條 じょう 自然 しぜん 定律 ていりつ 表明 ひょうめい 所有 しょゆう 只 ただ 因 いん 素的 すてき 運動 うんどう 都 と 是 ぜ 直線 ちょくせん 運動 うんどう 在 ざい 條 じょう 自然 しぜん 定律 ていりつ 裡 うら 笛 ふえ 確 かく 切 きり 聲明 せいめい 動態 どうたい 與 あずか 靜態 せいたい 是 ぜ 物體 ぶったい 的 てき 兩 りょう 種 たね 基本 きほん 狀態 じょうたい 只 ただ 有 ゆう 當 とう 承 うけたまわ 外在 がいざい 因 いん 素 もと 作用 さよう 物體 ぶったい 的 てき 基本 きほん 狀態 じょうたい 才 ざい 會 かい 有 ゆう 所 しょ 改變 かいへん 笛 ふえ 版本 はんぽん 的 てき 慣性 かんせい 定律 ていりつ 對 たい 代 だい 動力 どうりょく 學理 がくり 論 ろん 的 てき 助 すけ 益 えき 良 りょう 多 た 牛 うし 頓 ひたぶる 笛 ふえ 狀態 じょうたい 概念的 がいねんてき 基礎 きそ 性 せい [ 16] [ 22]
1673年 ねん 克 かつ 里 さと 安 やす 惠 めぐみ 更 さら 發表 はっぴょう 了 りょう 著作 ちょさく 擺鐘論 ろん 》。這本牛 うし 頓 ひたすら 非常 ひじょう 的 てき 著作 ちょさく 採用 さいよう 更 さら 明晰 めいせき 的 てき 架 か 重 じゅう 新 しん 導出 どうしゅつ 了 りょう 伽 とぎ 利 り 略 りゃく 的 てき 自由 じゆう 落體 らくたい 理論 りろん 惠 めぐみ 更 さら 物體 ぶったい 的 てき 運動 うんどう 提出 ていしゅつ 了 りょう 三 さん 個 こ 假設 かせつ 第 だい 第 だい 一 いち 個 こ 假設 かせつ 表明 ひょうめい 假設 かせつ 重力 じゅうりょく 不 ふ 存在 そんざい 假設 かせつ 空氣 くうき 不 ふ 會 かい 物體 ぶったい 的 てき 運動 うんどう 則 のり 任意 にんい 物體 ぶったい 的 てき 運動會 うんどうかい 是 ぜ 持續 じぞく 的 てき 直線 ちょくせん 運動 うんどう [ 16] [ 23]
物理 ぶつり 泰斗 たいと 艾 もぐさ 牛 うし 伽 とぎ 利 り 略 りゃく 的 てき 想 そう 法 ほう 導 しるべ 頓 ひたぶる 第 だい 一 いち 定律 ていりつ 不 ふ 施 ほどこせ 加 か 外力 がいりょく 則 のり 沒 ぼつ 有 ゆう 加速度 かそくど 因 いん 物體 ぶったい 會 かい 維持 いじ 速度 そくど 不變 ふへん 牛 うし 頓 ひたぶる 將 はた 第 だい 第 だい 慣性 かんせい 定律 ていりつ 的 てき 再 さい 次 つぎ 陳述 ちんじゅつ [ 註 6] [ 24] 原版 げんばん 第 だい 一 いち 定律 ていりつ 的 てき 英文 えいぶん 翻譯 ほんやく 為 ため [ 4]
Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.
中 ちゅう 文 ぶん 翻譯 ほんやく 為 ため
物體 ぶったい 會 かい 堅持 けんじ 靜止 せいし 或 ある 直線 ちょくせん 運動 うんどう 狀態 じょうたい 除 じょ 非 ひ 有 ゆう 外力 がいりょく 迫 はさま 使 し 改變 かいへん 狀態 じょうたい
寫 うつし 出 で 第 だい 一 いち 定律 ていりつ 後 ご 牛 うし 頓 ひたぶる 開始 かいし 他所 よそ 觀 かん 的 てき 各種 かくしゅ 物體 ぶったい 的 てき 自然 しぜん 運動 うんどう 像 ぞう 飛 ひ 箭 や 飛石 とびいし 一類 いちるい 的 てき 發射 はっしゃ 體 たい 假 かり 若 わか 不 ふ 被 ひ 空氣 くうき 的 てき 抗拒 こうきょ 不 ふ 被 ひ 重力 じゅうりょく 吸引 きゅういん 墜落 ついらく 會 かい 持續 じぞく 不 ふ 停 とま 地 ち 運動 うんどう 當 とう 旋轉 せんてん 時 じ 陀螺 內部的 てき 組成 そせい 粒子 りゅうし 沒 ぼつ 有 ゆう 被 ひ 在 ざい 一起 かずき 旋轉 せんてん 曲線 きょくせん 的 てき 切線 せっせん 線 せん 運動 うんどう 飛 ひ 開 ひらき 由 よし 組成 そせい 粒子 りゅうし 被 ひ 在 ざい 一起 かずき 假 かり 若 わか 不 ふ 地面 じめん 摩擦 まさつ 力 りょく 與 あずか 空氣 くうき 的 てき 損耗 そんこう 會 かい 永久 えいきゅう 不 ふ 息 いき 地 ち 共同 きょうどう 隨 ずい 著 ちょ 旋轉 せんてん 像 ぞう 行 くだり 星 ぼし 彗星 すいせい 一類 いちるい 的 てき 星 ほし 體 たい 移動 いどう 力 りょく 的 てき 自由 じゆう 空間 くうかん 會 かい 更 さら 長 ちょう 時期 じき 地 ち 維持 いじ 的 てき 運動 うんどう 軌道 きどう 在 ざい 牛 うし 頓 ひたぶる 並 なみ 沒 ぼつ 有 ゆう 提 ひっさげ 到 いた 第 だい 他所 よそ 專 せん 注 ちゅう 的 てき 問題 もんだい 是 ぜ 為 ため 什麼 いんも 在 ざい 一般 いっぱん 觀察 かんさつ 中 ちゅう 物體 ぶったい 的 てき 運動 うんどう 狀態 じょうたい 會 かい 被 ひ 改變 かいへん 他 た 認 みとめ 為 ため 原因 げんいん 是 ぜ 有 ゆう 空氣 くうき 地面 じめん 摩擦 まさつ 力 りょく 等 とう 等 とう 作用 さよう 體 たい 假 かり 若 わか 力 りょく 不 ふ 存在 そんざい 則 のり 運動 うんどう 中 ちゅう 的 てき 物體 ぶったい 會 かい 永遠 えいえん 不 ふ 停 とま 的 てき 速 そく 直線 ちょくせん 運動 うんどう [ 4]
似 に 有 ゆう 好 こう 幾 いく 位 い 自然 しぜん 哲學 てつがく 家 か 與 あずか 科學 かがく 家 か 分別 ふんべつ 獨立 どくりつ 地 ち 想 そう 出 で 了 りょう 慣性 かんせい 定律 ていりつ [ 註 7]
當 とう 物體 ぶったい 運動 うんどう 時 じ 只 ただ 有 ゆう 相對 そうたい 特定 とくてい 的 てき 物體 ぶったい 觀察 かんさつ 者 しゃ 或 ある 者 もの 時空 じくう 坐 すわ 標 しるべ 才能 さいのう 確實 かくじつ 顯示 けんじ 出 で 物理 ぶつり 行為 こうい 特定 とくてい 的 てき 標識 ひょうしき 稱 しょう 為 ため 參考 さんこう 系 けい 假 かり 若 わか 選擇 せんたく 了 りょう 不 ふ 適當 てきとう 的 てき 參考 さんこう 系 けい 則 のり 相關 そうかん 的 てき 運動 うんどう 定律 ていりつ 可能 かのう 會 かい 比較 ひかく 複雜 ふくざつ 在 ざい 慣性 かんせい 參考 さんこう 系 けい 中 ちゅう 力學 りきがく 定律 ていりつ 會 かい 展 てん 現出 げんしゅつ 最 さい 簡單 かんたん 的 てき 形式 けいしき 從 したがえ 参考 さんこう 系 けい 觀察 かんさつ 任 にん 何 なん 呈 てい 直 ちょく 動的 どうてき 參考 さんこう 系 けい 是 ぜ 慣性 かんせい 參考 さんこう 系 けい 否 いや 則 のり 是 ぜ 非 ひ 慣性 かんせい 參考 さんこう 系 けい 換 かわ 句 く 話 はなし 說 せつ 牛 うし 頓 ひたぶる 定律 ていりつ 滿足 まんぞく 伽 とぎ 利 り 略 りゃく 不變 ふへん 性 せい 即 そく 在 ざい 所有 しょゆう 慣性 かんせい 參考 さんこう 系 けい 裏 うら 牛 うし 頓 ひたぶる 定律 ていりつ 都 と 保持 ほじ 不變 ふへん [ 25] [ 26]
牛 うし 第 だい 依 よ 外界 がいかい 任 にん 何 なん 事物 じぶつ 独自 どくじ 存在 そんざい 的 てき 参考 さんこう 系 けい [ 註 8] 是 ぜ 在 ざい 中 ちゅう 自由 じゆう 物體 ぶったい 具有 ぐゆう 保持 ほじ 原 ばら 來 らい 運動 うんどう 狀態 じょうたい 的 てき 性質 せいしつ 性質 せいしつ 稱 たたえ 為 ため 慣性 かんせい 因 よし 第 だい 一 いち 定律 ていりつ 又 また 稱 しょう 為 ため 慣性 かんせい 定律 ていりつ 但 ただし 代物 しろもの 理学 りがく 的 てき 看 み 来 らい 存在 そんざい
在 ざい 牛 うし 頓 ひたぶる 時期 じき 固定 こてい 星 ぼし 體 からだ 時 どき 常 つね 被 ひ 用 よう 為 ため 參考 さんこう 系 けい 因 いん 為 ため 相對 そうたい 絕對 ぜったい 空間 くうかん 大 だい 靜止 せいし 不動 ふどう 在 ざい 那 な 對 たい 固定 こてい 星 ぼし 體 からだ 呈 てい 靜止 せいし 不動 ふどう 或 ある 直線 ちょくせん 運動 うんどう 的 てき 參考 さんこう 系 けい 中 ちゅう 牛 うし 頓 ひたぶる 運動 うんどう 定律 ていりつ 被 ひ 認 みとめ 為 ため 正確 せいかく 無 な 誤 あやま 但 ただし 是 ぜ 學者 がくしゃ 現在 げんざい 知道 ともみち 固定 こてい 星 ぼし 體 からだ 並 なみ 不 ふ 是 ぜ 固定 こてい 不動 ふどう 在 ざい 銀河系 ぎんがけい 固定 こてい 星 ぼし 體 からだ 會 かい 隨 ずい 著 ちょ 整 せい 個 こ 星 ほし 系 けい 旋轉 せんてん 顯示 けんじ 出 で 自 じ 行 くだり 銀河系 ぎんがけい 外的 がいてき 固定 こてい 星 ぼし 體 からだ 會 かい 從事 じゅうじ 自己 じこ 的 てき 運動 うんどう 可能 かのう 是 ぜ 因 いん 為 ため 宇宙 うちゅう 膨脹 ぼうちょう 本 ほん 動 どう 速度 そくど 等 ひとし 等 ひとし [ 27] [ 註 9] 現在 げんざい 慣性 かんせい 參考 さんこう 系 けい 的 てき 概念 がいねん 不 ふ 再 さい 絕對 ぜったい 空間 くうかん 或 ある 固定 こてい 星 ほし 體 たい 替 がえ 之 の 根據 こんきょ 在 ざい 某 ぼう 參考 さんこう 系 けい 中 ちゅう 物理 ぶつり 定律 ていりつ 的 てき 簡易 かんい 性質 せいしつ 學者 がくしゃ 可 か 參考 さんこう 系 けい 是 ぜ 否 ひ 為 ため 慣性 かんせい 參考 さんこう 系 けい 更 さら 確 かく 切 きり 假 かり 若 わか 虛 きょ 設 しつらえ 力 りょく 不 ふ 存在 そんざい 則 のり 參考 さんこう 系 けい 是 ぜ 慣性 かんせい 參考 さんこう 系 けい 否 ひ 則 そく 不 ふ 是 ぜ 慣性 かんせい 參考 さんこう 系 けい [ 29] [ 註 10]
實際 じっさい 不 ふ 是 ぜ 必要 ひつよう 條件 じょうけん 選擇 せんたく 固定 こてい 星 ほし 體 たい 來 らい 近似 きんじ 慣性 かんせい 參考 さんこう 系 けい 造成 ぞうせい 的 てき 誤差 ごさ 相當 そうとう 微小 びしょう 例 れい 地球 ちきゅう 繞 にょう 著 ちょ 太陽 たいよう 的 てき 公轉 こうてん 所產 しょさん 生 せい 的 てき 離 はなれ 心力 しんりょく 比 ひ 太陽 たいよう 繞 にょう 著 ちょ 銀河系 ぎんがけい 中心 ちゅうしん 的 てき 公轉 こうてん 所產 しょさん 生 せい 的 てき 離 はなれ 心力 しんりょく 要 よう 大 だい 三 さん 千 せん 萬 まん 倍 ばい 所以 ゆえん 在 ざい 研究 けんきゅう 太陽系 たいようけい 中 なか 星 ほし 體 たい 的 てき 運動 うんどう 時 じ 太陽 たいよう 是 ぜ 一 いち 個 こ 良好 りょうこう 的 てき 慣性 かんせい 參考 さんこう 系 けい [ 31]
麻 あさ 省 しょう 理工 りこう 學院 がくいん 物理 ぶつり 教授 きょうじゅ 瓦 かわら 列 れつ 文 ぶん Walter Lewin )講 こう 解 かい 牛 うし 頓 ひたぶる 第 だい 一 いち 定律 ていりつ 與 あずか 參考 さんこう 系 けい (MIT Course 8.01 ) [ 32]
^ 1.0 1.1 物理 ぶつり 学名 がくめい 定 じょう 委 い 物理 ぶつり 学名 がくめい 全国 ぜんこく 科学 かがく 技 わざ 定 じょう 委 い 公布 こうふ 版 はん 北京 ぺきん 科学 かがく 出版 しゅっぱん 社 しゃ 科学 かがく 文 ぶん 页面存 そん ,存 そん 互联网档案 あん ).^ 2.0 2.1 Halliday, Resnick & Walker 2005 ,第 だい 頁 ぺーじ ^ Santavy, I., Newton's first law, European Journal of Physics, 1986, 7 (2): 132–133, doi:10.1088/0143-0807/7/2/011 ^ 4.0 4.1 4.2 4.3 Newton 1846 ,第 だい 頁 ぺーじ ^ Pfister, Herbert, Newton's First Law Revisited, Foundations of Physics Letters, 2004, 17 (1): 49–64, doi:10.1023/B:FOPL.0000013003.96640.79 Newton's first law … was historically one of the first cornerstones of classical physics, … Neverthesis, in most mechanics textbooks little care is devoted to a logically clear formulation of Newton's first law. … John S. Rigden calls Newton's first law a “logician's nightmare,” but also expresses the biew that the law is a “wonder beyond description” ^ 6.0 6.1 Rigden, John, High thoughts about Newton's First Law, American Journal of Physics, 1998, 55 (4): 297, doi:10.1119/1.15191 ^ Einstein 1922 ,第 だい 頁 ぺーじ ^ 馬 うま 克 かつ 士 し 威 い 第 だい 頁 ぺーじ ^ Holton & Brush 2001 ,第 だい 頁 ぺーじ ^ 10.0 10.1 French 1971 ,第 だい 頁 ぺーじ ^ 11.0 11.1 11.2 11.3 11.4 11.5 O'Sullivan, Colm, Newton's Laws of Motion: Some interpretations of the formalism , American Journal of Physics, 1980, 48 (2): 131–133 [2018-08-13 ] , doi:10.1119/1.12186 原始 げんし 内容 ないよう 存 そん ^ Newton 1846 ,第 だい 頁 ぺーじ ^ Hesse 2008 ,第 だい 頁 ぺーじ ^ French 1971 ,第 だい 頁 ぺーじ ^ Cohen 2011 ,第 だい 頁 ぺーじ ^ 16.0 16.1 16.2 16.3 Cohen 2002 ,第 だい 頁 ぺーじ ^ Graneau & Graneau 2006 ,第 だい 頁 ぺーじ ^ Dugas 1988 ,第 だい 頁 ぺーじ ^ Frautschi 1986 ,第 だい 頁 ぺーじ ^ Mach 2010 ,第 だい 頁 ぺーじ ^ Frautschi 1986 ,第 だい 頁 ぺーじ ^ Slowik 2005 ^ Huygens, Christian. Horologium Oscillatorium (An English translation by Ian Bruce) . August 2013 [14 November 2013] . (原始 げんし 内容 ないよう 存 そん ^ Dugas 1988 ,第 だい 頁 ぺーじ ^ Landau & Lifshitz 1960 ,第 だい 頁 ぺーじ ^ Thornton 2004 ,第 だい 頁 ぺーじ ^ Balbi 2008 ,第 だい 頁 ぺーじ harvnb模 も 板 ばん 錯誤 さくご 無 む 指向 しこう 目標 もくひょう 幫助 ) ^ Abraham Loeb, Mark J. Reid, Andreas Brunthaler, Heino Falcke. Constraints on the proper motion of the Andromeda galaxy based on the survival of its satellite M33 (PDF) . The Astrophysical Journal. 2005, 633 (2): 894–898 [2011-11-30 ] . Bibcode:2005ApJ...633..894L arXiv:astro-ph/0506609 doi:10.1086/491644 原始 げんし 内容 ないよう 存 そん (PDF) 于2017-08-11). ^ Stachel 2002 ,第 だい 頁 ぺーじ ^ Kleppner & Kolenkow 2013 ,第 だい 頁 ぺーじ ^ Graneau & Graneau 2006 ,第 だい 頁 ぺーじ ^
Walter Lewin. Newton's First, Second, and Third Laws. MIT Course 8.01: Classical Mechanics, Lecture 6. (ogg) (videotape). Cambridge, MA USA: MIT OpenCourseWar. 事件 じけん 在 ざい [December 23, 2010] (英 えい .
Einstein, Albert, The Meaning of Relativity (PDF) , PRINCETON UNIVERSITY PRESS, 1922 [2019-03-27 ] , ISBN 978-1542694247原始 げんし 内容 ないよう 存 そん (PDF) 于2019-03-27) Cohen, I., Newton's concept of force and mass, with notes on the Laws of Motion, Cohen, I.; Smith, George (编), The Cambridge Companion to Newton, Cambridge University Press, 2002, ISBN 0-521-65177-8 Cohen, Michael, Classical Mechanics: a Critical Introduction , Michael Cohen, 2011 [2019-01-24 ] , (原始 げんし 内容 ないよう 存 そん Dugas, R., A History Of Mechanics, New York: Dover Publications, Inc., 1988, ISBN 0-486-65632-2 Frautschi, Steven, The Mechanical universe: mechanics and heat illustrated, Cambridge University Press, 1986, ISBN 9780521304320 French, Anthony, Newtonian Mechanics, 1971 Graneau, Peter; Graneau, Neal, In the Grip of the Distant Universe: The Science of Inertia, World Scientific, 2006, ISBN 978-981-256-754-3 Halliday, David; Resnick, Robert; Walker, Jerl, Fundamental of Physics 7th, USA: John Wiley and Sons, Inc., 2005, ISBN 0-471-23231-9 Hesse, Mary, Forces and Fields, A Study of Action at a Distance in the History of Physics, Philosophical Library, 2008, ISBN 978-0806530857 Holton, Gerald; Brush, Stephen, Physics, the Human Adventure 2nd, USA: Princeton University Press, 2001, ISBN 0-8135-2908-5 Kleppner, Daniel; Kolenkow, Robert, An Introduction to Mechanics 2nd, Cambridge University Press, 2013, ISBN 9780521198110 Landau, L. D.; Lifshitz, E. M., Mechanics, Pergamon Press, 1960 Mach, Ernst , The science of mechanics; a critical and historical account of its development , Watchmaker Publishing, 2010 [1919], ISBN 978-1603863254 馬 うま 克 かつ 士 し 威 い Matter and Motion , D.Van Nostrand, 1878 Newton, Isaac, Newton's Principia : the mathematical principles of natural philosophy , New York: Daniel Adee, 1846 網 もう 作者 さくしゃ 的 てき 英文 えいぶん 翻譯 ほんやく Slowik, Edward, Descartes' Physics , Stanford Encyclopedia of Philosophy, 2005, (原始 げんし 内容 ないよう 存 そん Stachel, John, Einstein from "B" to "Z", Springer, 2002, ISBN 0817641432 Thornton, Marion, Classical dynamics of particles and systems 5th, Brooks/Cole, 2004, ISBN 0534408966
表 おもて 述 じゅつ 形式 けいしき 基 もと 概念 がいねん 重 じゅう 要理 ようり 应用 科学 かがく 史 し 分 ぶん 支 ささえ



 . doi:10.1086/491644. (
. doi:10.1086/491644. (







