変換 へんかん P は直線 ちょくせん m の上 うえ 直交 ちょっこう 射影 しゃえい 線型 せんけい 代数 だいすう 学 がく 函数 かんすう 解析 かいせき 学 がく 射影 しゃえい 作用素 さようそ 単 たん 射影 しゃえい 英 えい projection 射影 しゃえい 投影 とうえい 一般 いっぱん 化 か 概念 がいねん 有限 ゆうげん 次元 じげん ベクトル空間 くうかん V の場合 ばあい V 上 うえ 線型 せんけい 変換 へんかん P : V → V であって、冪 べき 等 とう 律 りつ P 2 = P を満 み 言 い v の像 ぞう Pv を v の射影 しゃえい 射影 しゃえい 作用素 さようそ 空間 くうかん V を U ⊕W と直和 なおかず 分解 ぶんかい V の元 もと v = u + w (u ∈ U , w ∈ W ) を u に写 うつ 変換 へんかん 空間 くうかん 次元 じげん 無限 むげん 次元 じげん 場合 ばあい 連続 れんぞく 性 せい 考慮 こうりょ 例 たと ヒルベルト空間 くうかん
H
{\displaystyle {\mathcal {H}}}
射影 しゃえい 作用素 さようそ
H
{\displaystyle {\mathcal {H}}}
上 うえ 有界 ゆうかい 線型 せんけい 作用素 さようそ
P
∈
L
(
H
)
{\displaystyle P\in {\mathcal {L}}({\mathcal {H}})}
冪 べき 等 とう 律 りつ P 2 = P を満 み 言 い 自己 じこ 共役 きょうやく 性 せい P ∗ = P を持 も 直交 ちょっこう 射影 しゃえい 英 えい orthogonal projection )という。直交 ちょっこう 射影 しゃえい 単 たん 射影 しゃえい 呼 よ
この定義 ていぎ 抽象 ちゅうしょう 的 てき 投影 とうえい 図法 ずほう 考 かんが 方 かた 一般 いっぱん 化 か 定式 ていしき 化 か 幾何 きか 学 がく 的 てき 対象 たいしょう 上 うえ 射影 しゃえい 影響 えいきょう 対象 たいしょう 各 かく 点 てん 射影 しゃえい 影響 えいきょう 調 しら
直交 ちょっこう 射影 しゃえい [ 編集 へんしゅう ] 例 たと 三 さん 次元 じげん 空間 くうかん R 3 の点 てん x , y , z ) を点 てん x , y , 0) へ写 うつ 写像 しゃぞう xy -平面 へいめん 上 うえ 射影 しゃえい 写像 しゃぞう 行列 ぎょうれつ
P
=
[
1
0
0
0
1
0
0
0
0
]
{\displaystyle P={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}}
によって表現 ひょうげん 実際 じっさい 行列 ぎょうれつ P の任意 にんい 作用 さよう
P
[
x
y
z
]
=
[
x
y
0
]
{\displaystyle P{\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}x\\y\\0\end{bmatrix}}}
となり、これが射影 しゃえい 定 さだ P = P 2 を満 み
P
2
[
x
y
z
]
=
P
[
x
y
0
]
=
[
x
y
0
]
{\displaystyle P^{2}{\begin{bmatrix}x\\y\\z\end{bmatrix}}=P{\begin{bmatrix}x\\y\\0\end{bmatrix}}={\begin{bmatrix}x\\y\\0\end{bmatrix}}}
なる計算 けいさん 確 たし
(定義 ていぎ 後述 こうじゅつ 直交 ちょっこう 斜 はす 射影 しゃえい 簡単 かんたん 例 れい
P
=
[
0
0
α あるふぁ
1
]
{\displaystyle P={\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}}
を挙 あ 行列 ぎょうれつ 積 せき 定義 ていぎ 従 したが 計算 けいさん
P
2
=
[
0
0
α あるふぁ
1
]
[
0
0
α あるふぁ
1
]
=
[
0
0
α あるふぁ
1
]
=
P
{\displaystyle P^{2}={\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}{\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}={\begin{bmatrix}0&0\\\alpha &1\end{bmatrix}}=P}
故 ゆえ P が実際 じっさい 射影 しゃえい 分 わ
この射影 しゃえい P が直交 ちょっこう 射影 しゃえい α あるふぁ 限 かぎ
以下 いか 本節 ほんぶし 考 かんが 空間 くうかん 有限 ゆうげん 次元 じげん 仮定 かてい 場合 ばあい 射影 しゃえい 連続 れんぞく 性 せい 気 き
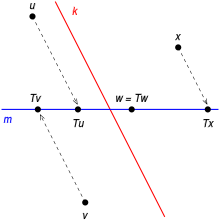
変換 へんかん T は k に沿 そ m の上 うえ 射影 しゃえい T の値域 ちいき m であり、T の零 れい 空間 くうかん k に等 ひと 本 ほん 項 こう 冒頭 ぼうとう 導入 どうにゅう 文 ぶん 述 の 射影 しゃえい P は冪 べき 等 とう 律 りつ P 2 = P を満 み 線型 せんけい 変換 へんかん
もととなるベクトル空間 くうかん W とする。W の部分 ぶぶん 線型 せんけい 空間 くうかん U および V が、それぞれ P の値域 ちいき 零 れい 空間 くうかん 核 かく 仮定 かてい 基本 きほん 的 てき 性質 せいしつ
P は U 上 うえ 恒等 こうとう 作用素 さようそ I として作用 さよう
∀
x
∈
U
,
P
x
=
x
.
{\displaystyle \forall x\in U,\quad Px=x.}
直和 なおかず 分解 ぶんかい W = U ⊕ V が成立 せいりつ W の各 かく x は U の元 もと u と V の元 もと v を用 もち x = u + v なる形 かたち 一意的 いちいてき 表 あらわ
u
=
P
x
,
v
=
x
−
P
x
=
(
I
−
P
)
x
{\displaystyle u=Px,\quad v=x-Px=(I-P)x}
などが成 な 立 た 射影 しゃえい 値域 ちいき 核 かく 互 たが 相補 そうほ 的 てき P と Q = I − P も同 おな 相補 そうほ 的 てき 作用素 さようそ Q もやはり射影 しゃえい 定 さだ Q の値域 ちいき P の核 かく Q の核 かく P の値域 ちいき 逆 ぎゃく 然 しか
このとき P を(核 かく V に沿 そ 値域 ちいき U の上 うえ 射影 しゃえい 言 い Q を U に沿 そ V の上 うえ 射影 しゃえい 呼 よ
ベクトル空間 くうかん 部分 ぶぶん 空間 くうかん 直 ちょく 和 わ 分解 ぶんかい 一般 いっぱん 一意的 いちいてき 従 したが 部分 ぶぶん 空間 くうかん V が与 あた 値域 ちいき 核 かく V となるような射影 しゃえい 一般 いっぱん 複数 ふくすう 存在 そんざい
射影 しゃえい スペクトル が {0, 1} に含 ふく
(
λ らむだ I
−
P
)
−
1
=
1
λ らむだ
I
+
1
λ らむだ (
λ らむだ −
1
)
P
{\displaystyle (\lambda I-P)^{-1}={\frac {1}{\lambda }}I+{\frac {1}{\lambda (\lambda -1)}}P}
から分 わ 射影 しゃえい 固有値 こゆうち 限 かぎ 対応 たいおう 固有 こゆう 空間 くうかん 射影 しゃえい 核 かく 値域 ちいき 他 た
自明 じめい 射影 しゃえい 最小 さいしょう 多項式 たこうしき
X
2
−
X
=
X
(
X
−
I
)
{\displaystyle X^{2}-X=X(X-I)}
相 あい 異 こと 一 いち 次 じ 因子 いんし 積 せき P は対 たい 角 かく 化 か 可能 かのう
直交 ちょっこう 射影 しゃえい [ 編集 へんしゅう ] 考 かんが 空間 くうかん 内積 ないせき 定義 ていぎ 直交 ちょっこう 性 せい 線型 せんけい 作用素 さようそ 自己 じこ 共軛 きょうやく 性 せい 内積 ないせき 付随 ふずい 概念 がいねん 用 もち 直交 ちょっこう 射影 しゃえい 値域 ちいき U と核 かく V とが互 たが 直交 ちょっこう 部分 ぶぶん 空間 くうかん 射影 しゃえい 射影 しゃえい 直交 ちょっこう 射影 しゃえい 必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん 自己 じこ 共軛 きょうやく 即 すなわ 実 じつ 空間 くうかん 場合 ばあい 直交 ちょっこう 基底 きてい 関 かん 表現 ひょうげん 行列 ぎょうれつ P が対称 たいしょう 行列 ぎょうれつ P = P T )であり、複素 ふくそ 空間 くうかん 場合 ばあい 表現 ひょうげん 行列 ぎょうれつ P がエルミート行列 ぎょうれつ (P = (P * )T ))となることである。実際 じっさい x , y が射影 しゃえい 定義 ていぎ 域 いき 属 ぞく Px ∈ U , y − Py ∈ V であり、かつ
⟨
∙
,
∙
⟩
{\displaystyle \langle \bullet ,\bullet \rangle }
正 せい 定値 ていち 内積 ないせき
⟨
P
x
,
y
−
P
y
⟩
=
(
P
x
)
⊤
(
y
−
P
y
)
=
x
⊤
(
P
⊤
−
P
⊤
P
)
y
=
x
⊤
(
P
−
P
⊤
P
)
⊤
y
{\displaystyle \langle Px,y-Py\rangle =(Px)^{\top }(y-Py)=x^{\top }(P^{\top }-P^{\top }P)y=x^{\top }(P-P^{\top }P)^{\top }y}
が成 な 立 た Px と y − Py とが任意 にんい x , y に関 かん 互 たが 直交 ちょっこう P = P T P (これは P = P T かつ P = P 2 に同値 どうち 限 かぎ
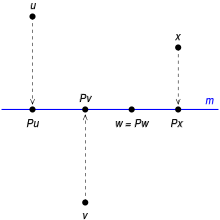
直線 ちょくせん 上 うえ 直交 ちょっこう 射影 しゃえい 場合 ばあい 最 もっと 簡単 かんたん 直線 ちょくせん 上 じょう 単位 たんい u をとれば、当該 とうがい 射影 しゃえい
P
u
=
u
u
⊤
{\displaystyle P_{u}=uu^{\top }}
で与 あた 作用素 さようそ u を変 か u に直交 ちょっこう 全 すべ 零 れい 化 か u を含 ふく 直線 ちょくせん 上 うえ 射影 しゃえい 正 ただ 見 み 簡単 かんたん 方法 ほうほう 勝手 かって x を直線 ちょくせん 上 じょう 成分 せいぶん 射影 しゃえい 考 かんが 垂直 すいちょく 成分 せいぶん 和 わ
x
:=
x
∥
+
x
⊥
{\displaystyle x:=x_{\parallel }+x_{\perp }}
と考 かんが 射影 しゃえい 施 ほどこ 平行 へいこう 同士 どうし 内積 ないせき 垂直 すいちょく 同士 どうし 内積 ないせき 性質 せいしつ
P
u
x
=
u
u
⊤
x
∥
+
u
u
⊤
x
⊥
=
u
|
x
∥
|
+
u
0
=
x
∥
{\displaystyle P_{u}x=uu^{\top }x_{\parallel }+uu^{\top }x_{\perp }=u|x_{\parallel }|+u0=x_{\parallel }}
を得 え
この等式 とうしき 任意 にんい 次元 じげん 部分 ぶぶん 空間 くうかん 上 うえ 直交 ちょっこう 射影 しゃえい 拡張 かくちょう u 1 , ..., u k 部分 ぶぶん 空間 くうかん U の正規 せいき 直交 ちょっこう 基底 きてい 各 かく 列 れつ u 1 , ..., u k k -次 じ 正方 せいほう 行列 ぎょうれつ A と書 か 所期 しょき 射影 しゃえい
P
A
=
A
A
⊤
{\displaystyle P_{A}=AA^{\top }}
で表 あらわ 内積 ないせき 使 つか
P
A
=
∑
i
⟨
u
i
,
∙
⟩
u
i
{\displaystyle P_{A}=\sum _{i}\langle u_{i},\bullet \rangle u_{i}}
と書 か 行列 ぎょうれつ A T は U の直交 ちょっこう 成分 せいぶん 消 き 部分 ぶぶん 等 とう 変換 へんかん A は U を考 かんが 全体 ぜんたい 空間 くうかん 埋 う 込 こ 等 ひとし 長 ちょう 変換 へんかん 従 したが PA の値域 ちいき A の終 おわり 空間 くうかん final space ) であり、また A T A が U 上 うえ 恒等 こうとう 変換 へんかん 明 あき
上記 じょうき 議論 ぎろん 正規 せいき 直交 ちょっこう 条件 じょうけん 落 お 即 すなわ u 1 , …, u k 必 かなら 正規 せいき 直交 ちょっこう 基底 きてい 列 れつ 持 も 行列 ぎょうれつ A と書 か 求 もと 射影 しゃえい
P
A
=
A
(
A
⊤
A
)
−
1
A
⊤
{\displaystyle P_{A}=A(A^{\top }A)^{-1}A^{\top }}
と書 か 場合 ばあい 行列 ぎょうれつ A は U の全体 ぜんたい 空間 くうかん 埋 う 込 こ 一般 いっぱん 等 とう 変換 へんかん 行列 ぎょうれつ A T A )−1 はノルムを回復 かいふく 正規 せいき 化 か 因子 いんし 実際 じっさい 階数 かいすう 作用素 さようそ uu T は ‖u ‖ ≠ 1 のとき射影 しゃえい u T u = ‖u ‖2 で割 わ 得 え u (u T u )−1 u T は u で張 は 部分 ぶぶん 空間 くうかん 上 うえ 射影 しゃえい
この射影 しゃえい 値域 ちいき 空間 くうかん 基底 きてい 枠 わく 張 は 生成 せいせい 元 もと 数 かず 次元 じげん 値 ね 大 おお 上記 じょうき 公式 こうしき
P
A
=
A
(
A
⊤
A
)
+
A
⊤
{\displaystyle P_{A}=A(A^{\top }A)^{+}A^{\top }}
という形 かたち
A
+
{\displaystyle A^{+}}
ムーア・ペンローズ擬似 ぎじ 逆 ぎゃく 行列 ぎょうれつ を表 あらわ 場合 ばあい 射影 しゃえい 作用素 さようそ 構成 こうせい 方法 ほうほう 無数 むすう 無数 むすう 可能 かのう 性 せい 一 ひと 過 す 注意 ちゅうい
あるいは、行列 ぎょうれつ
[
A
B
]
{\displaystyle [A\ B]}
正則 せいそく A T B = 0(つまり、B は A の零 れい 空間 くうかん 行列 ぎょうれつ
I
=
A
(
A
⊤
A
)
−
1
A
⊤
+
B
(
B
⊤
B
)
−
1
B
⊤
{\displaystyle I=A(A^{\top }A)^{-1}A^{\top }+B(B^{\top }B)^{-1}B^{\top }}
が成 な 立 た 直交 ちょっこう 条件 じょうけん 強 つよ 正則 せいそく 行列 ぎょうれつ W に対 たい A T WB = A T W T B = 0 が成 な 立 た
I
=
[
A
B
]
[
(
A
⊤
W
A
)
−
1
A
⊤
(
B
⊤
W
B
)
−
1
B
⊤
]
W
{\displaystyle I={\begin{bmatrix}A&B\end{bmatrix}}{\begin{bmatrix}(A^{\top }WA)^{-1}A^{\top }\\(B^{\top }WB)^{-1}B^{\top }\end{bmatrix}}W}
が成立 せいりつ
これらの公式 こうしき 転置 てんち 行列 ぎょうれつ 随伴 ずいはん 行列 ぎょうれつ 取 と 替 か 複素 ふくそ 内積 ないせき 空間 くうかん 成立 せいりつ
直交 ちょっこう 射影 しゃえい 射影 しゃえい 斜 はす 射影 しゃえい 呼 よ 直交 ちょっこう 射影 しゃえい 頻繁 ひんぱん 種 たね 射影 しゃえい 二 に 次元 じげん 描画 びょうが 空間 くうかん 図形 ずけい 表 あらわ 用 もち
斜 はす 射影 しゃえい 値域 ちいき 核 かく 定 さだ 与 あた 値域 ちいき 核 かく 持 も 射影 しゃえい 行列 ぎょうれつ 表現 ひょうげん 式 しき 次 つぎ 求 もと 射影 しゃえい 値域 ちいき 基底 きてい 成 な u 1 , …, u k 列 れつ 並 なら n × k 行列 ぎょうれつ A と書 か 射影 しゃえい 値域 ちいき 核 かく 互 たが 補 ほ 空間 くうかん 核 かく 次元 じげん n − k である。従 したが 射影 しゃえい 核 かく 直交 ちょっこう 補 ほ 空間 くうかん 次元 じげん k であり、v 1 , …, v k 基底 きてい 成 な 並 なら 行列 ぎょうれつ B と書 か 当該 とうがい 射影 しゃえい
P
=
A
(
B
⊤
A
)
−
1
B
⊤
{\displaystyle P=A(B^{\top }A)^{-1}B^{\top }}
によって定 さだ 公式 こうしき 上 うえ 直交 ちょっこう 射影 しゃえい 対 たい 拡張 かくちょう
体 からだ 上 じょう d -次元 じげん 空間 くうかん 上 じょう 射影 しゃえい P = P 2 は、その最小 さいしょう 多項式 たこうしき x 2 − x で相 あい 異 こと 一 いち 次 じ 因子 いんし 積 せき 分解 ぶんかい 対 たい 角 かく 化 か 可能 かのう 従 したが 適当 てきとう 基底 きてい 選 えら P は、r を P の階数 かいすう
P
=
I
r
⊕
0
d
−
r
{\displaystyle P=I_{r}\oplus 0_{d-r}}
なる形 かたち 表 あらわ I r r -次 じ 単位 たんい 行列 ぎょうれつ d −r 次数 じすう d − r の零 れい 行列 ぎょうれつ 複素 ふくそ 空間 くうかん 内積 ないせき 持 も 場合 ばあい 適当 てきとう 正規 せいき 直交 ちょっこう 基底 きてい 選 えら P の表現 ひょうげん 行列 ぎょうれつ
P
=
[
1
σ しぐま
1
0
0
]
⊕
⋯
⊕
[
1
σ しぐま
k
0
0
]
⊕
I
m
⊕
0
s
{\displaystyle P={\begin{bmatrix}1&\sigma _{1}\\0&0\end{bmatrix}}\oplus \cdots \oplus {\begin{bmatrix}1&\sigma _{k}\\0&0\end{bmatrix}}\oplus I_{m}\oplus 0_{s}}
なる形 かたち [8] σ しぐま 1 ≥ σ しぐま 2 ≥ … ≥ σ しぐま k k , s , m は整数 せいすう 実数 じっすう σ しぐま i 一意 いちい 定 さだ k + s + m = d であることに注意 ちゅうい I m s 因子 いんし 上 うえ P が直交 ちょっこう 射影 しゃえい 作用 さよう 最大 さいだい 不変 ふへん 空間 くうかん 対応 たいおう 故 ゆえ P 自体 じたい 直交 ちょっこう 射影 しゃえい k = 0 のとき、かつそのときに限 かぎ σ しぐま i P の斜 はす 成分 せいぶん 対応 たいおう
ノルム空間 くうかん 上 じょう 射影 しゃえい 作用素 さようそ [ 編集 へんしゅう ] 考 かんが 空間 くうかん X が(有限 ゆうげん 次元 じげん 限 かぎ ノルム空間 くうかん のとき、(有限 ゆうげん 次元 じげん 場合 ばあい 関係 かんけい 解析 かいせき 学 がく 的 てき 考 かんが X はバナッハ空間 くうかん であることを仮定 かてい
先 さき 述 の 代数 だいすう 的 てき 概念 がいねん 多 おお 文脈 ぶんみゃく 有効 ゆうこう 例 たと 互 たが 補 ほ 空間 くうかん 部分 ぶぶん 空間 くうかん X の直和 なおかず 分解 ぶんかい 与 あた 射影 しゃえい 定 さだ 逆 ぎゃく 射影 しゃえい 直和 なおかず 分解 ぶんかい 得 え 実際 じっさい X が直和 なおかず 分解 ぶんかい X = U ⊕ V を持 も P (u + v ) = u で定義 ていぎ 作用素 さようそ 値域 ちいき U および核 かく V の射影 しゃえい P 2 = P は明 あき 一方 いっぽう P が X 上 うえ 射影 しゃえい 即 すなわ P 2 = P を満 み I − P )2 = (I − P ) は容易 ようい 確 たし 即 すなわ I − P ) もまた射影 しゃえい 関係 かんけい 式 しき I = P + (I − P ) から X が Ran(P ) ⊕ Ran(I − P ) なる直和 なおかず 分解 ぶんかい 従 したが
しかし、有限 ゆうげん 次元 じげん 場合 ばあい 対照 たいしょう 的 てき 射影 しゃえい 一般 いっぱん 連続 れんぞく 限 かぎ 実際 じっさい X の部分 ぶぶん 空間 くうかん U がノルムの定 さだ 位相 いそう 関 かん U の上 うえ 射影 しゃえい 連続 れんぞく 同 おな 連続 れんぞく 射影 しゃえい P の値域 ちいき 必 かなら 部分 ぶぶん 空間 くうかん 更 さら 連続 れんぞく 射影 しゃえい 実 じつ 一般 いっぱん 連続 れんぞく 線型 せんけい 作用素 さようそ 核 かく 部分 ぶぶん 空間 くうかん 従 したが 連続 れんぞく 射影 しゃえい P は X の互 たが 補 おぎなえ 空間 くうかん 部分 ぶぶん 空間 くうかん 直 ちょく 和 わ 分解 ぶんかい X = Ran(P ) ⊕ Ker(P ) = Ran(P ) ⊕ Ran(I − P ) を与 あた
逆 ぎゃく 適当 てきとう 仮定 かてい 追加 ついか 成 な 立 た U を X の閉部分 ぶぶん 空間 くうかん X = U ⊕ V となる閉部分 ぶぶん 空間 くうかん V が存在 そんざい 場合 ばあい 限 かぎ 値域 ちいき U , 核 かく V となる射影 しゃえい P は連続 れんぞく 閉グラフ定理 ていり から従 したが 即 すなわ xn → x かつ Pxn → y とするとき、Px = y が示 しめ U が閉で、{Pxn } ⊂ U だから y は U に属 ぞく Py = y が成 な 立 た xn − Pxn = (I − P )xn → x − y である。このとき、V は閉で {(I − P )xn } ⊂ V だったから、x − y ∈ V 即 すなわ P (x − y ) = Px − Py = Px − y = 0 を得 え 主張 しゅちょう 示 しめ
今 いま 議論 ぎろん U , V がともに閉であるという仮定 かてい 効 き 部分 ぶぶん 空間 くうかん U が与 あた 空間 くうかん V の存在 そんざい 一般 いっぱん 保証 ほしょう ヒルベルト空間 くうかん では直交 ちょっこう 補 ほ 空間 くうかん 常 つね 空間 くうかん 場合 ばあい 一 いち 次元 じげん 部分 ぶぶん 空間 くうかん 常 つね 空間 くうかん 持 も ハーン・バナッハの定理 ていり から直 ただ 従 したが 実際 じっさい U を u が張 は 一 いち 次元 じげん 部分 ぶぶん 空間 くうかん 有界 ゆうかい 線型 せんけい 汎 ひろし 函数 かんすう φ ふぁい φ ふぁい u ) = 1 なるものがとれる。このとき、作用素 さようそ P (x ) := φ ふぁい x )u は P 2 = P を満足 まんぞく 射影 しゃえい φ ふぁい 有界 ゆうかい 性 せい P の連続 れんぞく 性 せい 出 で 従 したが P ) = Ran(I − P ) が U の閉補空間 くうかん
そうは言 い 開 ひらけ 写像 しゃぞう 定理 ていり 空間 くうかん 上 じょう 任意 にんい 連続 れんぞく 射影 しゃえい 開 ひらけ 写像 しゃぞう 言 い
応用 おうよう 進 すす 議論 ぎろん [ 編集 へんしゅう ] 射影 しゃえい 直交 ちょっこう 射影 しゃえい 他 た 線形 せんけい 代数 だいすう 問題 もんだい 計算 けいさん 重要 じゅうよう 役割 やくわり 果 は
上 うえ 述 の 射影 しゃえい 冪 べき 等 とう 作用素 さようそ 特別 とくべつ 解析 かいせき 学的 がくてき 直交 ちょっこう 射影 しゃえい 特性 とくせい 函数 かんすう 非 ひ 可 か 換 かわ 一般 いっぱん 化 か 可 か 測 はか 集合 しゅうごう 特性 とくせい 函数 かんすう 考 かんが 測度 そくど 論 ろん 始 はじ 冪 べき 等 とう 作用素 さようそ 例 たと 半 はん 単純 たんじゅん 多元 たげん 環 たまき 分類 ぶんるい 用 もち 想像 そうぞう 射影 しゃえい 作用素 さようそ 作用素 さようそ 環 たまき 論 ろん 文脈 ぶんみゃく 極 きわ 頻繁 ひんぱん 用 もち 特 とく フォン・ノイマン環 たまき はその射影 しゃえい 成 な 完備 かんび 束 たば 生成 せいせい
物理 ぶつり 応用 おうよう [ 編集 へんしゅう ] 量子 りょうし 論 ろん 条件 じょうけん 満 み 状態 じょうたい 全体 ぜんたい 状態 じょうたい 空間 くうかん (英語 えいご 版 ばん 部分 ぶぶん 空間 くうかん 考 かんが 量子力学 りょうしりきがく 的 てき 命題 めいだい 部分 ぶぶん 空間 くうかん 射影 しゃえい 演算 えんざん 子 こ 対応 たいおう 量子 りょうし 論理 ろんり
統計 とうけい 力学 りきがく 運動 うんどう 粗 あら 視 し 化 か 射影 しゃえい 演算 えんざん 子 こ 使 つか 定式 ていしき 化 か 方法 ほうほう 射影 しゃえい 演算 えんざん 子 こ 方法 ほうほう
分子 ぶんし 対称 たいしょう 性 せい 分子 ぶんし 振動 しんどう 格子 こうし 振動 しんどう 結晶 けっしょう 波動 はどう 関数 かんすう 任意 にんい 関数 かんすう 対称 たいしょう 性 せい 従 したが 関数 かんすう 作 つく 時 とき 射影 しゃえい 演算 えんざん 子 こ 用 もち 射影 しゃえい 演算 えんざん 子 こ 用 もち 既 すんで 約 やく 表現 ひょうげん 表現 ひょうげん 行列 ぎょうれつ 基底 きてい 関数 かんすう 基準 きじゅん 振動 しんどう 基準 きじゅん 求 もと
より一般 いっぱん 空間 くうかん 間 あいだ 写像 しゃぞう T : V → W が与 あた 同 おな 核 かく 直交 ちょっこう 補 ほ 空間 くうかん 上 じょう 等 とう 像 ぞう 要求 ようきゅう
(
ker
T
)
⊥
→
W
{\displaystyle (\ker T)^{\perp }\to W}
等 とう 特 とく 全 ぜん 射 しゃ 直交 ちょっこう 射影 しゃえい 場合 ばあい W が V の部分 ぶぶん 空間 くうかん リーマン幾何 きか 学 がく においてこのことはリーマン沈 しず 込 こ の定義 ていぎ 使 つか






















![{\displaystyle [A\ B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/530f52c1d0282e097abf01aa2eb948717b7ced0b)





