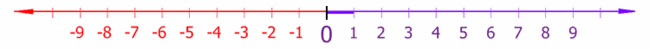正せいの数かずと負まけの数かず

数学すうがくにおける正せいの数かず（せいのすう、英えい: positive number, plus number, above number; 正数せいすう）は、0より大おおきい実数じっすうである。対照たいしょう的てきに負まけの数かず（ふのすう、英えい: negative number, minus number, below number; 負数ふすう）は、0より小ちいさい実数じっすうである。とくに初等しょとう数学すうがく・算術さんじゅつや初等しょとう数すう論ろんなどの文脈ぶんみゃくによっては、（暗黙あんもくの了解りょうかいのもと）特とくに断ことわりなく、より限定げんてい的てきな範囲はんいの正せいの有理数ゆうりすうや正せいの整数せいすうという意味いみで単たんに「正せいの数かず」と呼よんでいる場合ばあいがある。負まけの数かずも同様どうようである。

関数かんすう[編集へんしゅう]

符号ふごう関数かんすう[編集へんしゅう]

定義ていぎ域いきが実数じっすうであり、正数せいすうに対たいして1を、負数ふすうに対たいして−1を、ゼロに対たいして0を返かえす関数かんすう sgn(x) を定義ていぎできる。この関数かんすうは符号ふごう関数かんすうと呼よばれることがある

\operatorname {sgn}(x)=\left\{{\begin{matrix}-1&:x<0\\\;0&:x=0\\\;1&:x>0\end{matrix}}\right.

このとき（x=0の場合ばあいを除のぞき）以下いかの式しきが得えられる。

\operatorname {sgn}(x)={\frac {x}{|x|}}={\frac {|x|}{x}}={\frac {d{|x|}}{d{x}}}=2H(x)-1.

ここで |x| は x の絶対ぜったい値ちであり、H(x) はヘヴィサイドの階段かいだん関数かんすうである。微分びぶん法ほうも参照さんしょう。

複素ふくそ符号ふごう関数かんすう[編集へんしゅう]

定義ていぎ域いきが複素数ふくそすうであり、正数せいすうに対たいして1を、負数ふすうに対たいして-1を、ゼロに対たいして0を返かえす csgn(x) を定義ていぎできる。この関数かんすうは複素ふくそ符号ふごう関数かんすうと呼よばれることがある。

\operatorname {csgn} (x)=\left\{{\begin{matrix}-1&:x<0\\\;0&:x=0\\\;1&:x>0\end{matrix}}\right.

複素数ふくそすうの大小だいしょうは以下いかのように解釈かいしゃくする。

{\begin{cases}x>0\iff \operatorname {Re} (x)>0\vee (\operatorname {Re} (x)=0\land \operatorname {Im} (x)>0)\\x<0\iff \operatorname {Re} (x)<0\vee (\operatorname {Re} (x)=0\land \operatorname {Im} (x)<0)\\\end{cases}}

符号ふごう付つき数すうの算術さんじゅつ演算えんざん[編集へんしゅう]

加算かさんと減算げんざん[編集へんしゅう]

数列すうれつは、零れい・正数せいすう・負数ふすうの三さん種類しゅるいが組くみ合あわさって構成こうせいされており、基準きじゅん点てんが零れい、基準きじゅん点てんから増ふえている分ふんが正数せいすう、基準きじゅん点てんから減へっている分ふんが負数ふすうとなる。

従したがって、加算かさんと減算げんざんでは、負数ふすうは負債ふさいであり、正数せいすうは収益しゅうえきであると考かんがえることができる。同おなじく、時間じかんや世代せだいの距離きょりを数かぞえる場合ばあいにも、零れいは現在げんざいや自分じぶん、負数ふすうは過去かこや年上としうえ（親おやや祖父母そふぼなど）、正数せいすうは未来みらいや年下としした（子供こどもや孫まごなど）であると考かんがえることもできる。

負数ふすうを加くわえることは、対応たいおうする正数せいすうを減げんずることになる。逆ぎゃくに、負数ふすうを減げんずることは、対応たいおうする正数せいすうを加くわえることになる。

9 − 5 = 4

（9歳さい年下とししたの人物じんぶつと5歳さい年下とししたの人物じんぶつは、4歳さい離はなれている。）

7 − (−2) = 9

（7歳さい年下とししたの人物じんぶつと2歳さい年上としうえの人物じんぶつは、9歳さい離はなれている。）

−4 + 12 = 8

（¥4の負債ふさいがあって収益しゅうえきによる¥12の資産しさんを得えたら、純資産じゅんしさんは¥8である）（注ちゅう:純資産じゅんしさん＝資産しさん総額そうがく－負債ふさい総額そうがく）

5 + (−3) = 5 − 3 = 2

（¥5の資産しさんを持もっていて¥3の負債ふさいができたら、純資産じゅんしさんは¥2である）

–2 + (−5) = −2 − 5 = −7

（¥2の負債ふさいがあってさらに¥5の負債ふさいができたら、負債ふさいは合あわせて¥7になる）

減算げんざんと負ふ符号ふごうの概念がいねんの混乱こんらんを避さけるため、負ふ符号ふごうを上うえ付つきで書かく場合ばあいもある（ただし、会計かいけいでは負ふ符号ふごうを△で表現ひょうげんする）。

⁻2 + ⁻5 = ⁻2 − 5 = ⁻7

△2 + △5 = △2 − 5 = △7

正数せいすうをより小ちいさな正数せいすうから減げんずると、結果けっかは負まけとなる。

4 − 6 = −2

（¥4を持もっていて¥6を使つかったら、負債ふさい¥2が残のこる）

正数せいすうを任意にんいの負数ふすうから引ひくと、結果けっかは負まけとなる。

−3 − 6 = −9

（負債ふさいが¥3あってさらに¥6を使つかったら、負債ふさいは¥9となる）

負数ふすうを減げんずることは、対応たいおうする正数せいすうを加くわえることと等価とうかである。

5 − (−2) = 5 + 2 = 7

（純資産じゅんしさん¥5を持もっていて負債ふさいを¥2減へらしたら、新あらたな純資産じゅんしさんは¥7となる）

別べつの例れい

−8 − (−3) = −5

（負債ふさいが¥8あって負債ふさいを¥3減へらしたら、まだ¥5の負債ふさいが残のこる）

乗算じょうざん[編集へんしゅう]

負数ふすうを掛かけることは、正負せいふの方向ほうこうを逆転ぎゃくてんさせることになる。負数ふすうに正数せいすうを掛かけると、積せきは負数ふすうのままとなる。しかし、負数ふすうに負数ふすうを掛かけると、積せきは正数せいすうとなる^[1]。

(−20) × 3 = −60

（負債ふさい¥20を3倍ばいにすれば、負債ふさい¥60になる。）

(−40) × (−2) = 80

（後方こうほうへ毎時まいじ40km進すすむ車くるまは、2時じ間あいだ前まえには現在地げんざいちから前方ぜんぽうへ80kmの位置いちにいた。）

これを理解りかいする方法ほうほうの1つは、正数せいすうによる乗算じょうざんを、加算かさんの繰くり返かえしと見みなすことである。3 × 2 は各かくグループが2を含ふくむ3つのグループと考かんがえる。したがって、3 × 2 = 2 + 2 + 2 = 6 であり、当然とうぜん −2 × 3 = (−2) + (−2) + (−2) = −6 である。

負数ふすうによる乗算じょうざんも、加算かさんの繰くり返かえしと見みなすことができる。例たとえば、3 × −2は各かくグループが−2を含ふくむ3つのグループと考かんがえられる。

3 × −2 = (−2) + (−2) + (−2) = −6

これは乗算じょうざんの交換こうかん法則ほうそくを満みたすことに注意ちゅうい

3 × −2 = −2 × 3 = −6

「負数ふすうによる乗算じょうざん」と同おなじ解釈かいしゃくを負数ふすうに対たいしても適用てきようすれば、以下いかのようになる。

−4 × −3	= − (−4) − (−4) − (−4)
	= 4 + 4 + 4
	= 12

しかし形式けいしき的てきな視点してんからは、2つの負数ふすうの乗算じょうざんは、積せきの和わに対たいする分配ぶんぱい法則ほうそくによって直接ちょくせつ得えられる。

−1 × −1	= (−1) × (−1) + (−2) + 2
	= (−1) × (−1) + (−1) × 2 + 2
	= (−1) × (−1 + 2) + 2
	= (−1) × 1 + 2
	= (−1) + 2
	= 1

除算じょざん[編集へんしゅう]

除算じょざんも乗算じょうざんと同おなじく、負数ふすうで割わることは、正負せいふの方向ほうこうを逆転ぎゃくてんさせることになる。負数ふすうを正数せいすうで割わると、商しょうは負数ふすうのままとなる。しかし、負数ふすうを負数ふすうで割わると、商しょうは正数せいすうとなる。

被除数ひじょすうと除数じょすうの符号ふごうが異ことなるなら、商しょうは負数ふすうとなる。

(−90) ÷ 3 = −30

（負債ふさい¥90を3人にんで分わけると、負債ふさい¥30ずつ継承けいしょうされる。）

24 ÷ (−4) = −6

（東ひがしを正数せいすう、西にしを負数ふすうとする場合ばあい：4時じ間あいだ後ごに東ひがしへ24km地点ちてんに進すすむ車くるまは、1時じ間あいだ前まえには西にしへ6kmの位置いちにいる。）

両方りょうほうの数かずが同おなじ符号ふごうを持もつなら、商しょうは（両方りょうほうが負数ふすうであっても）正数せいすうとなる。

(−12) ÷ (−3) = 4

累乗るいじょう[編集へんしゅう]

累乗るいじょうは乗算じょうざんや除算じょざんと同おなじく、指数しすうを正数せいすうにすると、「n乗じょう」に倍増ばいぞうされる。しかし、指数しすうを負数ふすうにすると、「1 / n乗じょう」に分割ぶんかつされる。つまり、指数しすう n を正数せいすうにすると「n 回かい乗算じょうざんを繰くり返かえす」ことになるが、指数しすう n を負数ふすうにすると「n 回かい除算じょざんを繰くり返かえす」ことになる。

3³ = 27

（×3 ×3 ×3 = 27）

3⁻³ = 1/27

（÷3 ÷3 ÷3 = 1/27）

360 × 2³ = 2880

（360 ×2 ×2 ×2 = 2880）

36 × 5⁻¹ = 7.2

（36 ÷5 = 7.2）

負まけの整数せいすうと負まけでない整数せいすうの形式けいしき的てきな構成こうせい[編集へんしゅう]

有理数ゆうりすうの場合ばあいと同様どうよう、整数せいすうを自然しぜん数すうの順序じゅんじょ対たい (a, b) （これは整数せいすう a − b を表あらわしていると考かんがえることができる）を下したに述のべるようにして同一どういつ視ししたものとして定義ていぎすることによって自然しぜん数すうの集合しゅうごうNを整数せいすうの集合しゅうごうZに拡張かくちょうできる。これらの順序じゅんじょ対たいに対たいする加法かほうと乗法じょうほうの拡張かくちょうは以下いかの規則きそくによる。

(a, b) + (c, d) = (a + c, b + d)

(a, b) × (c, d) = (a × c + b × d, a × d + b × c)

ここで以下いかの規則きそくにより、これらの順序じゅんじょ対たいに同値どうち関係かんけい ~ を定義ていぎする。

(a, b) ~ (c, d) となるのは a + d = b + c なる場合ばあい、およびこの場合ばあいに限かぎる

この同値どうち関係かんけいは上記じょうきの加法かほうと乗法じょうほうの定義ていぎと矛盾むじゅんせず、ZをN²の ~ による商しょう集合しゅうごうとして定義ていぎできる。すなわち2つの順序じゅんじょ対たい (a, b) と (c, d) が上記じょうきの意味いみで同値どうちであるとき同一どういつ視しする。

さらに以下いかの通とおり全ぜん順序じゅんじょをZに定義ていぎできる。

(a, b) ≤ (c, d) となるのは a + d ≤ b + c となる場合ばあい、およびこの場合ばあいに限かぎる

これにより加法かほうの零れい元げんが (a, a) の形式けいしきで、(a, b) の加法かほうの逆ぎゃく元もとが (b, a) の形式けいしきで、乗法じょうほうの単位たんい元もとが (a + 1, a) の形式けいしきで導みちびかれ、減法げんぽうの定義ていぎが以下いかのように導みちびかれる。

(a, b) − (c, d) = (a + d, b + c).

負まけの数かずの起源きげん[編集へんしゅう]

長ながい間あいだ、問題もんだいに対たいする負まけの解かいは「誤あやまり」であると考かんがえられていた。これは、負数ふすうを実じつ世界せかいで見付みつけることができなかったためである（例たとえば、負数ふすうのリンゴを持もつことはできない）。その抽象ちゅうしょう概念がいねんは早はやければ紀元前きげんぜん100年ねん – 紀元前きげんぜん50年ねんには認識にんしきされていた。中国ちゅうごくの『九きゅう章しょう算術さんじゅつ』には図ずの面積めんせきを求もとめる方法ほうほうが含ふくまれている。赤あかい算木さんぎで正せいの係数けいすうを、黒くろい算木さんぎで負まけの係数けいすうを示しめし、負まけの数かずがかかわる連立れんりつ方程式ほうていしきを解とくことができた。紀元きげん後ご7世紀せいきごろに書かかれた古代こだいインドの『バクシャーリー写本しゃほん』^[2]は"+"を負ふ符号ふごうとして使つかい、負まけの数かずによる計算けいさんを行おこなっていた。これらが現在げんざい知しられている最古さいこの負まけの数かずの使用しようである。

プトレマイオス朝あさエジプトではディオファントスが3世紀せいきに『算術さんじゅつ』で 4x + 20 = 0 （解かいは負まけとなる）と等価とうかな方程式ほうていしきに言及げんきゅうし、この方程式ほうていしきはばかげていると言いっており、古代こだい地中海ちちゅうかい世界せかいに負数ふすうの概念がいねんがなかったことを示しめしている。

7世紀せいきの間あいだに、負数ふすうはインドで負債ふさいを表あらわすために使つかわれていた。インドの数学すうがく者しゃブラーマグプタは『ブラーフマスプタ・シッダーンタ』（628年ねん）において、今日きょうも使つかわれている一般いっぱん化かされた形式けいしきの解かいの公式こうしきを作つくるために、負数ふすうを使つかうことについて論ろんじている。彼かれは二に次じ方程式ほうていしきの負まけの解かいを発見はっけんし、負数ふすうと零れいが関かかわる演算えんざんに関かんする規則きそくも与あたえている。彼かれは正数せいすうを「財産ざいさん」、零れいを「0 (cipher)」、負まけの数かずを「借金しゃっきん」と呼よんだ^[3]^[4]。12世紀せいきのインドで、バースカラ2世せいも二に次じ方程式ほうていしきに負まけの根ねを与あたえていたが、問題もんだいの文脈ぶんみゃくでは不適切ふてきせつなものとして負まけの根ねを拒絶きょぜつしている。

8世紀せいき以降いこう、イスラム世界せかいはブラーマグプタの著書ちょしょのアラビア語ご訳わけから負まけの数かずを学まなび、紀元きげん1000年ねん頃ころまでには、アラブの数学すうがく者しゃは負債ふさいに負まけの数かずを使つかうことを理解りかいしていた。

負まけの数かずの知識ちしきは、最終さいしゅう的てきにアラビア語ごとインド語ごの著書ちょしょのラテン語らてんご訳わけを通とおしてヨーロッパに到達とうたつした。

しかし、ヨーロッパの数学すうがく者しゃはそのほとんどが、17世紀せいきまで負数ふすうの概念がいねんに抵抗ていこうを見みせた。ただしフィボナッチは、『算盤そろばんの書しょ』（1202年ねん）の第だい13章しょうで負数ふすうを負債ふさいと解釈かいしゃくし、後のちには『精華せいか』で損失そんしつと解釈かいしゃくして金融きんゆう問題もんだいに負まけの解かいを認みとめた。同時どうじに、中国人ちゅうごくじんは右みぎ端はしのゼロでない桁けたに斜線しゃせんを引ひくことによって負数ふすうを表あらわした。ヨーロッパ人じんの著書ちょしょで負数ふすうが使つかわれたのは、15世紀せいき中なかのシュケによるものが最初さいしょであった。彼かれは負数ふすうを指数しすうとして使つかったが、「馬鹿ばかげた数かず」であると呼よんだ。

イギリスの数学すうがく者しゃフランシス・マセレス[2]は1759年ねん、負数ふすうは存在そんざいしないという結論けつろんに達たっした^[5]。

負数ふすうは現代げんだいまで十分じゅうぶんに理解りかいされていなかった。つい18世紀せいきまで、スイスの数学すうがく者しゃレオンハルト・オイラーは負数ふすうが無限むげん大だいより大おおきいと信しんじており（この見解けんかいはジョン・ウォリスと共通きょうつうである）、方程式ほうていしきが返かえすあらゆる負まけの解かいを意味いみがないものとして無視むしすることが普通ふつうだった^[6]。負数ふすうが無限むげん大だいより大おおきいという論拠ろんきょは、 ${\frac {1}{x}}$ の商しょうと、x が正せいの側がわから x = 0 の点てんに近ちかづき、交差こうさした時とき何なにが起おきるかの考察こうさつによって生しょうじている。

一般いっぱん化か[編集へんしゅう]

正せいの行列ぎょうれつ[編集へんしゅう]

正せい行列ぎょうれつ: 実み行列ぎょうれつAについて、Aが負まけでないということを、Aのすべての成分せいぶんが負まけでない、というふうに定さだめることができる。このとき、実じつ行列ぎょうれつのうちには正せいとも負まけとも言いえないものもあることになる。また、実み行列ぎょうれつAについて、Aの全すべての正方せいほう部分ぶぶん行列ぎょうれつの行列ぎょうれつ式しきが負まけでないとき、Aのことを完全かんぜんに非負ひふ（行列ぎょうれつ理論りろん）あるいは、完全かんぜんに正ただし（コンピュータ科学かがく者しゃ）と呼よぶことがある。
正せい定値ていち行列ぎょうれつ: 一方いっぽうで、線形せんけい代数だいすう学がく的てきな観点かんてんから、実みのる対称たいしょう行列ぎょうれつやより一般いっぱんに複素ふくそエルミート行列ぎょうれつについて、上うえとは異ことなった正負せいふの概念がいねんがしばしば用もちいられる。エルミート行列ぎょうれつAは、その固有値こゆうちの全すべてが負まけでないときに、負まけでない（あるいは単たんに、正せいである）とよばれる。Aが負まけでないということはある行列ぎょうれつBについてAが B*.Bと書かけることと同値どうちになる（行列ぎょうれつの定値ていち性せいも参照さんしょう）。無限むげん次元じげんの場合ばあいとして、函数かんすう解析かいせき学がくにおける正せい作用素さようその概念がいねんが対応たいおうする。

正せい錐きり[編集へんしゅう]

「順序じゅんじょ群ぐん#定義ていぎ」、「順序じゅんじょ線型せんけい空間くうかん#正せい錐きり（英語えいご版ばん）」、および「順序じゅんじょ体たい#定義ていぎ」も参照さんしょう

抽象ちゅうしょう代だい数学すうがくの言葉ことばでは、正せいの数かずの全体ぜんたい $P$ は実数じっすう全体ぜんたい $ℝ$ の正せい錐きり（英語えいご版ばん）と呼よばれる対象たいしょうを成なす。これにより $ℝ$ は加法かほうに関かんして順序じゅんじょ群ぐん、加法かほうと乗法じょうほうに関かんして順序じゅんじょ体たいと呼よばれる構造こうぞうを持もち、また逆ぎゃくに、順序じゅんじょ群ぐんや順序じゅんじょ体たいとしての $ℝ$ の正せい錐きり $P$ が与あたえられれば「正せいの数かずとは $P$ の任意にんいの元もとのことである」と述のべることができる。

$xy$ -平面へいめん $ℝ 2$ の第だい一いち象限しょうげん（英語えいご版ばん）や $xyz$ -空間くうかん $ℝ 3$ の $x > 0, y > 0, z > 0$ なる八はち分ふん象限しょうげん（英語えいご版ばん）などが順序じゅんじょ線型せんけい空間くうかんとしての正せい錐きりの例れいであり、この構造こうぞうに「錐きり」の名称めいしょうがつけられている理由りゆうをみることができる。

これらのような順序じゅんじょ構造こうぞうにおいて、正せい錐きりはそれぞれの付加ふか構造こうぞうによって記述きじゅつできる良よい性質せいしつを様々さまざまに持もつ。

函数かんすう解析かいせき学がくにおける正せい作用素さようそ全体ぜんたいの成なす凸とつ錐きりもまたそのような例れいであり、より抽象ちゅうしょう的てきにバナッハ環たまき、C*-環たまきにおける正せいの元もと（英語えいご版ばん）などが考察こうさつの対象たいしょうとなる。

脚注きゃくちゅう[編集へんしゅう]

^ 『相対そうたい論ろんの式しきを導みちびいてみよう、そして、人ひとに話はなそう』（小笠おがさ英志えいじ、ベレ出版しゅっぱん、ISBN 978-4860642679）の PP.121-127にマイナス×マイナスがプラスになることの小学生しょうがくせいも納得なっとくできる説明せつめいが書かいてある。
^ Hayashi, Takao (2005), "Indian Mathematics", in Flood, Gavin, The Blackwell Companion to Hinduism, Oxford: Basil Blackwell, 616 pages, pp. 360-375, ISBN 978-1-4051-3251-0.
^ Colva Roney-Dougal, Lecturer in Pure Mathematics at the University of St Andrews, stated this on the BBC Radio 4 "In Our Time", on Negative Numbers, 9 March 2006.
^ Knowledge Transfer and Perceptions of the Passage of Time, ICEE-2002 Keynote Address by Colin Adamson-Macedo. [1]
^ Maseres, Francis, 1731–1824. A dissertation on the use of the negative sign in algebra, 1758.
^ Alberto A. Martinez, Negative Math: How Mathematical Rules Can Be Positively Bent, Princeton University Press, 2006; おもに1600年代ねんだいから1900年代ねんだい前半ぜんはんにかけての、負数ふすうに関かんする論争ろんそうの歴史れきし。

外部がいぶリンク[編集へんしゅう]

Weisstein, Eric W. "Positive Number". mathworld.wolfram.com (英語えいご). / Weisstein, Eric W. "Negative Number". mathworld.wolfram.com (英語えいご).
positive - PlanetMath.（英語えいご） / negative number - PlanetMath.（英語えいご）
positive number in nLab
Definition:Positive Number at ProofWiki / Definition:Negative Number at ProofWiki
BBC Radio 4 series "In Our Time", on Negative Numbers, March 9, 2006（英語えいご）
Endless Examples & Exercises: Operations With Signed Integers（英語えいご）
Math Forum: Ask Dr. Math FAQ: Negative Times a Negative（英語えいご）

[1] 『相対そうたい論ろんの式しきを導みちびいてみよう、そして、人ひとに話はなそう』（小笠おがさ英志えいじ、ベレ出版しゅっぱん、ISBN 978-4860642679）の PP.121-127にマイナス×マイナスがプラスになることの小学生しょうがくせいも納得なっとくできる説明せつめいが書かいてある。

[2] Hayashi, Takao (2005), "Indian Mathematics", in Flood, Gavin, The Blackwell Companion to Hinduism, Oxford: Basil Blackwell, 616 pages, pp. 360-375, ISBN 978-1-4051-3251-0.

[dougal1-3] Colva Roney-Dougal, Lecturer in Pure Mathematics at the University of St Andrews, stated this on the BBC Radio 4 "In Our Time", on Negative Numbers, 9 March 2006.

[zeros1-4] Knowledge Transfer and Perceptions of the Passage of Time, ICEE-2002 Keynote Address by Colin Adamson-Macedo. [1]

[maseres1-5] Maseres, Francis, 1731–1824. A dissertation on the use of the negative sign in algebra, 1758.

[martinez1-6] Alberto A. Martinez, Negative Math: How Mathematical Rules Can Be Positively Bent, Princeton University Press, 2006; おもに1600年代ねんだいから1900年代ねんだい前半ぜんはんにかけての、負数ふすうに関かんする論争ろんそうの歴史れきし。

[1]

[2]

[3]

[4]

[5]

[6]