この項目 こうもく 三 さん 次元 じげん 空間 くうかん 内 ない 二 に 次元 じげん 図形 ずけい 説明 せつめい 一般 いっぱん 球面 きゅうめん 超 ちょう 球面 きゅうめん 中身 なかみ 詰 つ 立体 りったい 図形 ずけい 球体 きゅうたい 覧 らん
球面 きゅうめん 二 に 次元 じげん 投影 とうえい 図 ず 初等 しょとう 幾何 きか 学 がく ユークリッド幾何 きか 学 がく において、球面 きゅうめん 英 えい sphere [ 注釈 ちゅうしゃく ] 三 さん 次元 じげん 空間 くうかん 与 あた 定点 ていてん 距離 きょり 一 いち 定値 ていち r をもつような点 てん 全体 ぜんたい 成 な 集合 しゅうごう 与 あた 定点 ていてん 球面 きゅうめん 中心 ちゅうしん 距離 きょり r をこの球面 きゅうめん 半径 はんけい 球面 きゅうめん 中心 ちゅうしん 通 とお 直線 ちょくせん 球面 きゅうめん 切 き 取 と 線分 せんぶん 長 なが 常 つね 一定 いってい 半径 はんけい 二 に 倍 ばい 等 ひと 球面 きゅうめん 直径 ちょっけい 呼 よ
「どの方向 ほうこう 観察 かんさつ 半径 はんけい r の円 えん 見 み 立体 りったい 図形 ずけい 定義 ていぎ
緩 ゆる 方 いかた 数学 すうがく 以外 いがい 文脈 ぶんみゃく 球 たま 球面 きゅうめん 球体 きゅうたい 同義語 どうぎご 用 もち 意味 いみ 入 い 違 ちが 数学 すうがく 的 てき 球面 きゅうめん sphere ) は三 さん 次元 じげん ユークリッド空間 くうかん に埋 う 込 こ 二 に 次元 じげん 閉曲面 めん であり、球体 きゅうたい ball ) は三 さん 次元 じげん 空間 くうかん 内 ない 球面 きゅうめん 球面 きゅうめん 囲 かこ 内側 うちがわ 球面 きゅうめん 含 ふく 場合 ばあい 特 とく 閉球体 きゅうたい 」と呼 よ 囲 かこ 領域 りょういき 球面 きゅうめん 含 ふく 場合 ばあい 開 ひらき 球体 きゅうたい 呼 よ
この区別 くべつ 必 かなら 守 まも 特 とく 古 ふる 文献 ぶんけん 中身 なかみ 詰 つ 図形 ずけい 球 たま 二 に 次元 じげん 場合 ばあい 円 えん 中身 なかみ 詰 つ 円 えん 板 ばん 意味 いみ 境界 きょうかい 円周 えんしゅう 意味 いみ 同 おな
two orthogonal radii of a sphere 解析 かいせき 幾何 きか 学 がく (x 0 , y 0 , z 0 ) を中心 ちゅうしん 半径 はんけい r の球面 きゅうめん 球面 きゅうめん
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
+
(
z
−
z
0
)
2
=
r
2
{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}}
満 み 点 てん (x , y , z ) 全体 ぜんたい 軌跡 きせき
a, b, c, d, e は実数 じっすう a ≠ 0
x
0
:=
−
b
a
,
y
0
:=
−
c
a
,
z
0
:=
−
d
a
,
ρ ろー :=
b
2
+
c
2
+
d
2
−
a
e
a
2
{\displaystyle x_{0}:={\frac {-b}{a}},\quad y_{0}:={\frac {-c}{a}},\quad z_{0}:={\frac {-d}{a}},\quad \rho :={\frac {b^{2}+c^{2}+d^{2}-ae}{a^{2}}}}
書 か 上記 じょうき 方程式 ほうていしき
f
(
x
,
y
,
z
)
:=
a
(
x
2
+
y
2
+
z
2
)
+
2
(
b
x
+
c
y
+
d
z
)
+
e
=
0
{\displaystyle f(x,y,z):=a(x^{2}+y^{2}+z^{2})+2(bx+cy+dz)+e=0}
形 かたち 一般 いっぱん 形 かたち 方程式 ほうていしき x 2 , y 2 , z 2 係数 けいすう 等 ひと xy, yz, zx の項 こう 持 も 三 さん 変数 へんすう 二 に 次 じ 多項式 たこうしき 方程式 ほうていしき 与 あた 以下 いか 何 いず 一 ひと 成 な 立 た
ρ ろー 方程式 ほうていしき 解 かい 実 み 点 てん 存在 そんざい 虚 きょ 球 だま imaginary sphere ) の方程式 ほうていしき 呼 よ ρ ろー 方程式 ほうていしき f (x , y , z ) = 0中心 ちゅうしん 一 いち 点 てん P 0 ≔ (x 0 , y 0 , z 0 )解 かい 点 てん 球 だま point sphere ) の方程式 ほうていしき 言 い ρ ろー f (x , y , z ) = 0P 0 中心 ちゅうしん 半径 はんけい r ≔ √ ρ ろー 球面 きゅうめん 方程式 ほうていしき 上 うえ 対照 たいしょう 場合 ばあい 実 じつ 球 たま real sphere ) の方程式 ほうていしき 言 い 上記 じょうき 方程式 ほうていしき a = 0f (x , y , z ) = 0平面 へいめん 方程式 ほうていしき 平面 へいめん 無限 むげん 遠 とお 点 てん 中心 ちゅうしん 半径 はんけい 無限 むげん 大 だい 球 たま 考 かんが
(x 0 , y 0 , z 0 ) を中心 ちゅうしん 半径 はんけい r の球面 きゅうめん 上 じょう 点 てん
{
x
=
x
0
+
r
sin
(
φ ふぁい )
cos
(
θ しーた )
y
=
y
0
+
r
sin
(
φ ふぁい )
sin
(
θ しーた )
z
=
z
0
+
r
cos
(
φ ふぁい )
(
0
≤
φ ふぁい ≤
π ぱい ,
0
≤
θ しーた <
2
π ぱい )
{\displaystyle {\begin{cases}x=x_{0}+r\sin(\varphi )\cos(\theta )\\y=y_{0}+r\sin(\varphi )\sin(\theta )\\z=z_{0}+r\cos(\varphi )\end{cases}}\qquad (0\leq \varphi \leq \pi ,\;0\leq \theta <2\pi )}
媒介 ばいかい 表示 ひょうじ
原点 げんてん 中心 ちゅうしん 任意 にんい 半径 はんけい 持 も 球面 きゅうめん 微分 びぶん 形式 けいしき
x
d
x
+
y
d
y
+
z
d
z
=
0
x{\mathit {dx}}+y{\mathit {dy}}+z{\mathit {dz}}=0
積分 せきぶん 曲面 きょくめん 微分 びぶん 形 がた 方程式 ほうていしき 位置 いち (x , y , z ) と速度 そくど (dx , dy , dz ) が全 ぜん 球面 きゅうめん 亙 わた 常 つね 互 たが 直交 ちょっこう 事実 じじつ 反映 はんえい
球面 きゅうめん 円周 えんしゅう 任意 にんい 直径 ちょっけい 軸 じく 回転 かいてん 回転 かいてん 曲面 きょくめん 構成 こうせい 円周 えんしゅう 特別 とくべつ 種類 しゅるい 楕円 だえん 球面 きゅうめん 特別 とくべつ 種類 しゅるい 回転 かいてん 楕円 だえん 面 めん 円 えん 回転 かいてん 代 か 楕円 だえん 長 ちょう 軸 じく 軸 じく 回転 かいてん 長 ちょう 球 たま 短 たん 軸 じく 軸 じく 扁 ひらた 球 だま
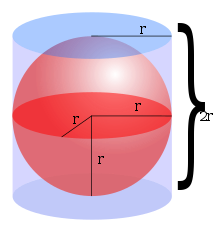
球面 きゅうめん 外接 がいせつ 円筒 えんとう 三 さん 次元 じげん 空間 くうかん 球面 きゅうめん 囲 かこ 体積 たいせき 厳密 げんみつ 言 い 球体 きゅうたい 体積 たいせき 古典 こてん 的 てき 球 たま 体積 たいせき 呼 よ 半径 はんけい r として
V
=
4
3
π ぱい
r
3
{\displaystyle V={\frac {4}{3}}\pi r^{3}}
与 あた 公式 こうしき 導 みちび 最初 さいしょ 人 ひと アルキメデス で、球面 きゅうめん 囲 かこ 体積 たいせき 球面 きゅうめん 外接 がいせつ 円筒 えんとう 円筒 えんとう 高 たか 底面 ていめん 直径 ちょっけい 球面 きゅうめん 直径 ちょっけい 等 ひと 間 あいだ 体積 たいせき 二 に 倍 ばい 等 ひと 示 しめ 導 みちび 主張 しゅちょう カヴァリエリの原理 げんり から得 え 公式 こうしき 積分 せきぶん 使 つか 導 みちび 原点 げんてん 中心 ちゅうしん 半径 はんけい r の球 たま 想定 そうてい 輪切 わぎ 積分 せきぶん 法 ほう (英語 えいご 版 ばん 中心 ちゅうしん x -軸 じく 沿 そ x = −r x = r 並 なら 無限 むげん 個 こ 積 つ 重 かさ 無限 むげん 薄 うす 円柱 えんちゅう 円 えん 板 ばん 体積 たいせき 総和 そうわ 球面 きゅうめん 体積 たいせき 計算 けいさん 球面 きゅうめん 座標 ざひょう 系 けい 体積 たいせき 要素 ようそ
d
V
:=
r
2
sin
(
θ しーた )
d
r
d
θ しーた
d
φ ふぁい
{\textstyle dV:=r^{2}\sin(\theta ){\mathit {dr}}\,{\mathit {d\theta }}\,{\mathit {d\varphi }}}
積分 せきぶん 同 おな 結果 けっか 得 え
半径 はんけい r の球面 きゅうめん 表面積 ひょうめんせき
A
:=
4
π ぱい
r
2
{\displaystyle A:=4\pi r^{2}}
与 あた 公式 こうしき 最初 さいしょ 発見 はっけん 者 しゃ アルキメデス は[ 6] 外接 がいせつ 円筒 えんとう 側面 そくめん 射影 しゃえい 面積 めんせき 保 たも 事実 じじつ 公式 こうしき 導 みちび
公式 こうしき 導 みちび 別 べつ 方 かた 同 おな 半径 はんけい r の球 たま 体積 たいせき r に関 かん 微分 びぶん 等 ひと 事実 じじつ 利用 りよう 半径 はんけい r の球 たま 内部 ないぶ 全 ぜん 体積 たいせき 半径 はんけい 0 から r までの無限 むげん 薄 うす 球 たま 殻 から 無限 むげん 個 こ 半径 はんけい 垂直 すいちょく 積 つ 重 かさ 体積 たいせき 総和 そうわ 捉 とら 理解 りかい 無限 むげん 薄 うす 条件 じょうけん 各 かく 球 たま 殻 から 内側 うちがわ 外側 そとがわ 表面積 ひょうめんせき 差 さ 無限 むげん 小 しょう 半径 はんけい r に対応 たいおう 球 たま 殻 から 体積 たいせき 単 たん 半径 はんけい r の球面 きゅうめん 表面積 ひょうめんせき 無限 むげん 小 ちい 厚 あつ 積 せき 得 え 注意 ちゅうい 球面 きゅうめん 座標 ざひょう 系 けい 球面 きゅうめん 面積 めんせき 要素 ようそ dA ≔ r 2 sin(θ しーた dθ しーた φ ふぁい 積分 せきぶん 導出 どうしゅつ
球面 きゅうめん 同 どう 一 いち 平面 へいめん 上 じょう 四 よん 点 てん 指定 してい 一意 いちい 決定 けってい 一般 いっぱん 通 とお 点 てん 平面 へいめん 接 せっ 条件 じょうけん 四 よっ 球面 きゅうめん 一意 いちい 決 き 性質 せいしつ 平面 へいめん 上 じょう 円 えん 同 どう 一直線 いっちょくせん 上 じょう 三 さん 点 てん 一意 いちい 決 き 性質 せいしつ 三 さん 次元 じげん 空間 くうかん 版 ばん 見 み 帰結 きけつ 球面 きゅうめん 一 ひと 円 えん 円 えん 属 ぞく 平面 へいめん 上 じょう 一 いち 点 てん 通 とお 意味 いみ 一意 いちい 決定 けってい
ふたつの球面 きゅうめん 方程式 ほうていしき 共通 きょうつう 解 かい 調 しら 球面 きゅうめん 円 えん 確認 かくにん 含 ふく 平面 へいめん 交 まじ 球面 きゅうめん 根 ね 面 めん radical plane ) という。根 ね 面 めん 実 じつ 平面 へいめん 虚 きょ 円 えん 二 ふた 球面 きゅうめん 共通 きょうつう 実 み 点 てん 持 も 点 てん 円 えん 二 ふた 球面 きゅうめん 一 いち 点 てん 接 せっ 得 え
交円上 じょう 実 み 点 てん 二 ふた 球面 きゅうめん 間 あいだ 成 な 角 かく 点 てん 各 かく 球面 きゅうめん 接 せっ 平面 へいめん 定義 ていぎ 二 に 面 めん 角 かく 言 い 二 ふた 球面 きゅうめん 上 じょう 点 てん 同 おな 角度 かくど 交 まじ 球面 きゅうめん 直角 ちょっかく 交 まじ 必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん 球面 きゅうめん 中心 ちゅうしん 間 あいだ 距離 きょり 平方 へいほう 半径 はんけい 平方和 へいほうわ 等 ひと
相 そう 異 こと 二 ふた 球面 きゅうめん 方程式 ほうていしき f (x , y , z ) = 0g (x , y , z ) = 0対 たい
s
f
(
x
,
y
,
z
)
+
t
g
(
x
,
y
,
z
)
=
0
{\displaystyle sf(x,y,z)+tg(x,y,z)=0}
助 じょ 変数 へんすう s, t の任意 にんい 値 ね 対 たい 球面 きゅうめん 方程式 ほうていしき 与 あた 適当 てきとう t, s に対 たい 方程式 ほうていしき 満足 まんぞく 球面 きゅうめん 族 ぞく 球面 きゅうめん 生成 せいせい 球面 きゅうめん 定 さだ 球 たま 束 たば 球面 きゅうめん 束 たば pencil of spheres ) と呼 よ 定義 ていぎ 球面 きゅうめん 平面 へいめん 無限 むげん 遠 とお 点 てん 中心 ちゅうしん 半径 はんけい 無限 むげん 大 だい 場合 ばあい 許 ゆる 生成 せいせい 球面 きゅうめん 両方 りょうほう 平面 へいめん 場合 ばあい 球面 きゅうめん 束 たば 成 な 球面 きゅうめん 平面 へいめん 球面 きゅうめん 束 たば 一 ひと 平面 へいめん 生成 せいせい 球面 きゅうめん 根 ね 面 めん
球面 きゅうめん 束 たば 平面 へいめん 以下 いか 三種 さんしゅ 分類 ぶんるい
生成 せいせい 球面 きゅうめん 実 じつ 円 えん C ならば、球面 きゅうめん 束 たば C を含 ふく 球面 きゅうめん 根 ね 面 めん 含 ふく 全体 ぜんたい 成 な 族 ぞく 球面 きゅうめん 束 たば 属 ぞく 通常 つうじょう 球面 きゅうめん 平面 へいめん 意味 いみ 中心 ちゅうしん 軌跡 きせき 中心 ちゅうしん 直線 ちょくせん C の中心 ちゅうしん 通 とお 根 ね 面 めん 直交 ちょっこう 直線 ちょくせん 上 じょう 生成 せいせい 球面 きゅうめん 虚 きょ 円 えん 球面 きゅうめん 束 たば 属 ぞく 球面 きゅうめん 虚 きょ 円 えん 通 とお 通所 つうしょ 球面 きゅうめん 交 まじ 共通 きょうつう 実 み 点 てん 属 ぞく 球面 きゅうめん 中心 ちゅうしん 直線 ちょくせん 根 ね 面 めん 虚 きょ 円 えん 含 ふく 平面 へいめん 球面 きゅうめん 束 たば 属 ぞく 直交 ちょっこう 生成 せいせい 球面 きゅうめん 点 てん 円 えん A ならば、束 たば 属 ぞく 球面 きゅうめん 全 すべ 点 てん A において接 せっ 根 ね 面 めん 束 たば 属 ぞく 球面 きゅうめん 共通 きょうつう 接 せっ 平面 へいめん 中心 ちゅうしん 直線 ちょくせん A において根 ね 面 めん 直交 ちょっこう 根 ね 面 めん 上 じょう 固定 こてい 点 てん 束 たば 属 ぞく 任意 にんい 球面 きゅうめん 引 ひ 接線 せっせん 長 なが 球面 きゅうめん 依 よ 同 おな
根 ね 面 めん 束 たば 属 ぞく 球面 きゅうめん 直交 ちょっこう 任意 にんい 球面 きゅうめん 中心 ちゅうしん 描 えが 軌跡 きせき 等 ひと 言 い 球面 きゅうめん 束 たば 属 ぞく 球面 きゅうめん 任意 にんい 直交 ちょっこう 球面 きゅうめん 束 たば 属 ぞく 球面 きゅうめん 直交 ちょっこう 中心 ちゅうしん 束 たば 根 ね 面 めん 上 じょう
球 たま 中心 ちゅうしん 通 とお 直線 ちょくせん 上 じょう 球面 きゅうめん 上 じょう 点 てん 対 たい 直線 ちょくせん 球面 きゅうめん 交点 こうてん 対蹠 たいしょ 点 てん (英語 えいご 版 ばん 呼 よ 球 たま 中心 ちゅうしん 半径 はんけい 共有 きょうゆう 球面 きゅうめん 上 じょう 円 えん 大円 だいえん 言 い 大円 だいえん 球面 きゅうめん 二 ふた 合同 ごうどう 図形 ずけい 分 わ 球面 きゅうめん 平面 へいめん 切断 せつだん (英語 えいご 版 ばん 球面 きゅうめん 切断 せつだん 球面 きゅうめん 断面 だんめん 球面 きゅうめん 切断 せつだん 円 えん 大円 だいえん 小 しょう 円 えん (英語 えいご 版 ばん 呼 よ [ 12]
二 ふた 相 そう 異 こと 非 ひ 対蹠 たいしょ 点 てん 間 あいだ 球面 きゅうめん 沿 そ 最短 さいたん 距離 きょり 二 に 点 てん 結 むす 一 ひと 大円 だいえん 二 に 点 てん 切 き 取 と 二 ふた 弧 こ 小 ちい 精確 せいかく 大 おお 長 なが 大円 だいえん 距離 きょり 備 そな 球面 きゅうめん 上 じょう 大円 だいえん リーマン円 えん (英語 えいご 版 ばん
球面 きゅうめん 上 じょう 特定 とくてい 点 てん 任意 にんい 選 えら 北極 ほっきょく 対蹠 たいしょ 点 てん 南極 なんきょく 呼 よ 両 りょう 極点 きょくてん 等距離 とうきょり 大円 だいえん 赤道 あかみち 二 ふた 極点 きょくてん 結 むす 大円 だいえん 子午線 しごせん 経線 けいせん 呼 よ 球 たま 内部 ないぶ 通 とお 両極 りょうきょく 結 むす 直線 ちょくせん 自転 じてん 軸 じく 呼 よ 赤道 せきどう 平行 へいこう 球面 きゅうめん 上 じょう 円 えん 緯線 いせん 語法 ごほう 近似 きんじ 的 てき 楕円 だえん 体 たい 地球 ちきゅう 惑星 わくせい 対 たい 用 もち ジオイド も参照 さんしょう
球面 きゅうめん 中心 ちゅうしん 含 ふく 任意 にんい 平面 へいめん 球面 きゅうめん 合同 ごうどう 半球 はんきゅう 面 めん hemisphere ) に分割 ぶんかつ 球面 きゅうめん 中心 ちゅうしん 通 とお 交 まじ 任意 にんい 平面 へいめん 四 よっ 球面 きゅうめん 楔 くさび 形 がた (英語 えいご 版 ばん 球面 きゅうめん 二 に 角形 かくがた 細分 さいぶん 割 わり 図形 ずけい 頂点 ちょうてん 平面 へいめん 上 じょう 対蹠 たいしょ 点 てん (英語 えいご 版 ばん 一致 いっち
球面 きゅうめん 対蹠 たいしょ 点 てん 同一 どういつ 視 し 商 しょう 実 じつ 射影 しゃえい 平面 へいめん (英語 えいご 版 ばん 呼 よ 曲面 きょくめん 赤道 せきどう 対蹠 たいしょ 点 てん 同一 どういつ 視 し 北半球 きたはんきゅう 見 み
この半球 はんきゅう 面 めん リーマン円 えん (英語 えいご 版 ばん 最適 さいてき 面積 めんせき 最小 さいしょう 等 とう 長 ちょう 充填 じゅうてん 予想 よそう (英語 えいご 版 ばん [訳語 やくご 疑問 ぎもん 点 てん
球面 きゅうめん 概念 がいねん 任意 にんい 次元 じげん 対 たい 一般 いっぱん 化 か 自然 しぜん 数 すう n に対 たい n -次元 じげん 球面 きゅうめん n -sphere") をしばしば Sn と書 か 中心 ちゅうしん 定点 ていてん 半径 はんけい 決 き 距離 きょり r の位置 いち n + 1次元 じげん 空間 くうかん 内 ない 点 てん 軌跡 きせき 定義 ていぎ 特 とく
零 れい 次元 じげん 球面 きゅうめん S 0 実数 じっすう 直線 ちょくせん 内 うち 間 あいだ [−r , r ] の両 りょう 端点 たんてん 一 いち 次元 じげん 球面 きゅうめん S 1 半径 はんけい r の円周 えんしゅう 二 に 次元 じげん 球面 きゅうめん S 2 通常 つうじょう 球面 きゅうめん 三 さん 次元 じげん 球面 きゅうめん S 3 四 よん 次元 じげん 空間 くうかん 内 ない 超 ちょう 球面 きゅうめん 表 あらわ n > 2超 ちょう 球面 きゅうめん [ 注釈 ちゅうしゃく ] 文献 ぶんけん 余 よ 次元 じげん (英語 えいご 版 ばん 限 かぎ 超 ちょう 球面 きゅうめん 呼 よ [ 注釈 ちゅうしゃく ] 場合 ばあい 稀 まれ 文脈 ぶんみゃく 注意 ちゅうい
Sn は、特 とく 単位 たんい 球面 きゅうめん 原点 げんてん 中心 ちゅうしん 単位 たんい 半径 はんけい 球面 きゅうめん 表 あらわ 用 もち
(n − 1次元 じげん 単位 たんい 超 ちょう 球面 きゅうめん 表面積 ひょうめんせき ガンマ函数 かんすう Γ がんま z )用 もち
2
π ぱい
n
/
2
Γ がんま (
n
/
2
)
{\displaystyle {\frac {2\pi ^{n/2}}{\Gamma (n/2)}}}
与 あた
より一般 いっぱん 距離 きょり 空間 くうかん (E , d ) において、中心 ちゅうしん x および半径 はんけい r > 0球面 きゅうめん 距離 きょり 球面 きゅうめん d (x ,y ) = r 点 てん y の軌跡 きせき 定義 ていぎ
中心 ちゅうしん E の「原点 げんてん 捉 とら 識別 しきべつ 点 てん 例 たと ノルム空間 くうかん は原点 げんてん 持 も 距離 きょり 空間 くうかん 定義 ていぎ 記法 きほう 点 てん 現 あらわ 半径 はんけい 1 に取 と 単位 たんい 球面 きゅうめん 呼 よ 従来 じゅうらい 通 どお
距離 きょり 球体 きゅうたい 場合 ばあい 異 こと 距離 きょり 球体 きゅうたい 十分 じゅうぶん 大 おお 半径 はんけい 持 も 場合 ばあい 空 そら 集合 しゅうごう 得 え 例 たと Z n ユークリッド距離 きょり を入 い 半径 はんけい r の球面 きゅうめん 空 そら r 2 n 個 こ 整数 せいすう 平方和 へいほうわ 書 か 限 かぎ
位相 いそう 幾何 きか 学 がく n + 1次元 じげん 位相 いそう 球体 きゅうたい 境界 きょうかい 同相 どうしょう 空間 くうかん n -次元 じげん 位相 いそう 球面 きゅうめん 定義 ていぎ n -次元 じげん 球面 きゅうめん 通常 つうじょう n -次元 じげん 球面 きゅうめん 同相 どうしょう 必 かなら 距離 きょり 付 つ
零 れい 次元 じげん 位相 いそう 球面 きゅうめん 離散 りさん 位相 いそう 入 はい 点 てん 対 たい 一 いち 次元 じげん 位相 いそう 球面 きゅうめん 同相 どうしょう 違 ちが 除 のぞ 円周 えんしゅう 任意 にんい 結 むす 目 め 一 いち 次元 じげん 位相 いそう 球面 きゅうめん 二 に 次元 じげん 位相 いそう 球面 きゅうめん 同相 どうしょう 違 ちが 除 のぞ 通常 つうじょう 球面 きゅうめん 例 たと 任意 にんい 楕円 だえん 体 たい 二 に 次元 じげん 位相 いそう 球面 きゅうめん n -次元 じげん 位相 いそう 球面 きゅうめん Sn と書 か 位相 いそう 球面 きゅうめん 境界 きょうかい コンパクト 位相 いそう 多様 たよう 体 たい 例 れい 必 かなら 可 か 微分 びぶん 多様 たよう 体 たい 滑 なめ 多様 たよう 体 たい 滑 なめ 場合 ばあい 球面 きゅうめん 微分 びぶん 同相 どうしょう 限 かぎ
ハイネ–ボレルの被覆 ひふく 定理 ていり により n -次元 じげん 球面 きゅうめん 分 わ 実際 じっさい 球面 きゅうめん 連続 れんぞく 函数 かんすう ‖ x ‖ による一 いち 点 てん 集合 しゅうごう 逆 ぎゃく 像 ぞう 集合 しゅうごう Sn は有界 ゆうかい
驚嘆 きょうたん 三 さん 次元 じげん 空間 くうかん 内 ない 自己 じこ 交叉 こうさ 許 ゆる 通常 つうじょう 球面 きゅうめん 一切 いっさい 切 き 目 め 入 い 裏返 うらがえ 一連 いちれん 方法 ほうほう 球 たま 裏返 うらがえ (英語 えいご 版 ばん 呼 よ
球面 きゅうめん 上 じょう 大円 だいえん ユークリッドの平面 へいめん 幾何 きか 学 がく 基本 きほん 要素 ようそ 点 てん 直線 ちょくせん 球面 きゅうめん 上 じょう 点 てん 通常 つうじょう 意味 いみ 定義 ていぎ 直線 ちょくせん 相当 そうとう 測地 そくち 線 せん 場合 ばあい 具体 ぐたい 的 てき 大円 だいえん 大円 だいえん 定義 ていぎ 特徴 とくちょう 上 うえ 点 てん 含 ふく 平面 へいめん 球 たま 中心 ちゅうしん 通 とお 弧 こ 長 ちょう 距離 きょり 測 はか 球面 きゅうめん 上 じょう 任意 にんい 二 に 点 てん 結 むす 最短 さいたん 経路 けいろ 点 てん 含 ふく 大円 だいえん 点 てん 切 き 取 と 円弧 えんこ 短 みじか 与 あた 証明 しょうめい
古典 こてん 幾何 きか 学 がく 多 おお 定理 ていり 球面 きゅうめん 幾何 きか 学 がく 真 しん 球面 きゅうめん 上 じょう 古典 こてん 幾 いく 何 なん 公準 こうじゅん 満足 まんぞく 平行 へいこう 線 せん 公準 こうじゅん 成立 せいりつ 真 しん 定理 ていり 存在 そんざい 球面 きゅうめん 三角 さんかく 法 ほう 角 かく 大円 だいえん 間 あいだ 定義 ていぎ 球面 きゅうめん 三角 さんかく 法 ほう 通常 つうじょう 三角 さんかく 法 ほう 様々 さまざま 点 てん 異 こと 例 たと 球面 きゅうめん 三角形 さんかっけい 内角 ないかく 和 わ 常 つね 180° より大 おお 任意 にんい 互 たが 相似 そうじ (英語 えいご 版 ばん 球面 きゅうめん 三角形 さんかっけい 合同 ごうどう
球面 きゅうめん 法 ほう 法 ほう 平面 へいめん 法 ほう 断面 だんめん 曲 きょく 率 りつ 断面 だんめん 曲 きょく 率 りつ 球面 きゅうめん 対 たい 与 あた 点 てん 通 とお 各 かく 法 ほう 断面 だんめん 同 おな 半径 はんけい 球 たま 半径 はんけい 等 ひと 持 も 円 えん 球面 きゅうめん 上 じょう 任意 にんい 点 てん 臍 ほぞ 点 てん 意味 いみ ダフィット・ヒルベルト とシュテファン・コーン゠フォッセン (英語 えいご 版 ばん 著書 ちょしょ Geometry and the Imagination [ 13] 彼 かれ 球面 きゅうめん 性質 せいしつ 記述 きじゅつ 性質 せいしつ 球面 きゅうめん 一意 いちい 決定 けってい 論 ろん 半径 はんけい 無限 むげん 大 だい 球面 きゅうめん 看做 みな 平面 へいめん 満足 まんぞく 性質 せいしつ
「球面 きゅうめん 上 じょう 点 てん 一 ひと 定点 ていてん 同一 どういつ 距離 きょり 定点 ていてん 点 てん 距離 きょり 比 ひ 一定 いってい [注釈 ちゅうしゃく 前半 ぜんはん 球面 きゅうめん 通常 つうじょう 定義 ていぎ 球面 きゅうめん 一意 いちい 決定 けってい 後半 こうはん 容易 ようい 導 みちび 円周 えんしゅう 対 たい ペルガのアポロニウス の結果 けっか 同様 どうよう 従 したが 後半 こうはん 内容 ないよう 平面 へいめん 満 み
「球面 きゅうめん 等高線 とうこうせん 平面 へいめん 切断 せつだん 円 えん [注釈 ちゅうしゃく 性質 せいしつ 球面 きゅうめん 一意 いちい 定義 ていぎ
「球面 きゅうめん 幅 はば 一定 いってい 周 しゅう 長 ちょう 一定 いってい [注釈 ちゅうしゃく 曲面 きょくめん 幅 はば 平行 へいこう 接 せっ 平面 へいめん 対 たい 間 あいだ 距離 きょり 測 はか 他 ほか 定 てい 幅 はば 凸 とつ 面 めん マイスナーの立体 りったい (英語 えいご 版 ばん 曲面 きょくめん 周 しゅう 長 ちょう 曲面 きょくめん 平面 へいめん 上 じょう 直交 ちょっこう 射影 しゃえい 像 ぞう 境界 きょうかい 外周 がいしゅう 長 なが 性質 せいしつ 各々 おのおの 他 た 性質 せいしつ 導 みちび
「球面 きゅうめん 上 じょう 臍 ほぞ 点 てん (英語 えいご 版 ばん [注釈 ちゅうしゃく 球面 きゅうめん 法線 ほうせん 球 っきゅう 中心 ちゅうしん 放射状 ほうしゃじょう 延 の 直線 ちょくせん 曲面 きょくめん 上 じょう 任意 にんい 点 てん 法 ほう 方向 ほうこう 曲面 きょくめん 直角 ちょっかく 法線 ほうせん 含 ふく 平面 へいめん 法 ほう 断面 だんめん 呼 よ 曲線 きょくせん 曲線 きょくせん 曲 きょく 率 りつ 法 ほう 曲 きょく 率 りつ 呼 よ 多 おお 曲面 きょくめん 対 たい 上 うえ 点 てん 多 おお 異 こと 切断 せつだん 対 たい 異 こと 曲 きょく 率 りつ 持 も 曲 きょく 率 りつ 中 なか 最大 さいだい 最小 さいしょう 値 ね 持 も 主 しゅ 曲 きょく 率 りつ 言 い 任意 にんい 面 めん 少 すく 四 よっ 臍 ほぞ 点 てん 呼 よ 点 てん 持 も 臍 ほぞ 点 てん 断面 だんめん 曲 きょく 率 りつ 特 とく 主 しゅ 曲 きょく 率 りつ 等 ひと 臍 ほぞ 点 てん 曲面 きょくめん 球面 きゅうめん 極 きわ 近似 きんじ 点 てん 見 み
球面 きゅうめん 対 たい 全 すべ 法 ほう 断面 だんめん 曲 きょく 率 りつ 等 ひと 任意 にんい 点 てん 臍 ほぞ 点 てん 性質 せいしつ 満 み 曲面 きょくめん 球面 きゅうめん 平面 へいめん 限 かぎ
「球面 きゅうめん 中心 ちゅうしん 曲面 きょくめん 持 も [注釈 ちゅうしゃく 与 あた 法 ほう 断面 だんめん 対 たい 断面 だんめん 曲 きょく 率 りつ 等 ひと 曲 きょく 率 りつ 持 も 曲面 きょくめん 接 せっ 円 えん 存在 そんざい 中心 ちゅうしん 線 せん 法線 ほうせん 上 じょう 載 の 例 たと 最大 さいだい 最小 さいしょう 断面 だんめん 曲 きょく 率 りつ 対応 たいおう 中心 ちゅうしん 点 てん 焦点 しょうてん 呼 よ 中心 ちゅうしん 点 てん 全体 ぜんたい 成 な 集合 しゅうごう 焦 こげ 面 めん (英語 えいご 版 ばん 成 な
大半 たいはん 曲面 きょくめん 焦 こげ 面 めん 二 に 葉 よう 曲面 きょくめん 曲面 きょくめん 二 ふた 集合 しゅうごう 成 な 葉 は 臍 ほぞ 点 てん 交 まじ 場合 ばあい 特別 とくべつ 管状 かんじょう 曲面 きょくめん (英語 えいご 版 ばん 場合 ばあい 一葉 いちよう 曲線 きょくせん 一 いち 葉 よう 曲面 きょくめん 円錐 えんすい 円筒 えんとう トーラス 、サイクライド (英語 えいご 版 ばん 場合 ばあい 二 に 葉 よう 曲線 きょくせん 成 な 球面 きゅうめん 場合 ばあい 任意 にんい 接触 せっしょく 円 えん 中心 ちゅうしん 球 っきゅう 中心 ちゅうしん 焦 こげ 面 めん 一 いち 点 てん 性質 せいしつ 球面 きゅうめん 対 たい 一意 いちい
「球面 きゅうめん 任意 にんい 測地 そくち 線 せん 閉曲線 へいきょくせん [注釈 ちゅうしゃく 測地 そくち 線 せん 曲面 きょくめん 上 じょう 曲線 きょくせん 二 に 点 てん 間 あいだ 最短 さいたん 距離 きょり 与 あた 平面 へいめん 上 じょう 直線 ちょくせん 概念 がいねん 一般 いっぱん 化 か 球面 きゅうめん 上 じょう 測地 そくち 線 せん 大円 だいえん 性質 せいしつ 満足 まんぞく 曲面 きょくめん 他 ほか
「与 あた 体積 たいせき 持 も 立体 りったい 中 なか 球 たま 表面積 ひょうめんせき 最 もっと 小 ちい 与 あた 表面積 ひょうめんせき 持 も 立体 りったい 中 なか 球 たま 最 もっと 大 おお 体積 たいせき 持 も 一 ひと [注釈 ちゅうしゃく 等 とう 周 しゅう 不等式 ふとうしき 従 したが 性質 せいしつ 球面 きゅうめん 一意 いちい 定義 ていぎ 定義 ていぎ 仕方 しかた シャボン玉 だま のようなものと思 おも 玉 だま 決 き 体積 たいせき 囲 かこ 体積 たいせき 対 たい 表面積 ひょうめんせき 表面張力 ひょうめんちょうりょく 極小 きょくしょう 最小 さいしょう 化 か 決 き 自由 じゆう 浮 う 玉 だま 球面 きゅうめん 近似 きんじ 重力 じゅうりょく 外力 がいりょく 玉 だま 形状 けいじょう 歪 いが
「与 あた 表面積 ひょうめんせき 持 も 凸 とつ 立体 りったい 球面 きゅうめん 最 もっと 小 ちい 全 ぜん 平均 へいきん 曲 きょく 率 りつ 持 も [注釈 ちゅうしゃく 平均 へいきん 曲 きょく 率 りつ (英語 えいご 版 ばん 二 ふた 主 しゅ 曲 きょく 率 りつ 平均 へいきん 球面 きゅうめん 全 すべ 点 てん 二 ふた 主 しゅ 曲 きょく 率 りつ 一定 いってい 平均 へいきん 曲 きょく 率 りつ 一定 いってい
「球面 きゅうめん 一定 いってい 平均 へいきん 曲 きょく 率 りつ 持 も [注釈 ちゅうしゃく 球面 きゅうめん 境界 きょうかい 特異 とくい 点 てん 正 せい 一定 いってい 平均 へいきん 曲 きょく 率 りつ 持 も 唯一 ゆいいつ 埋 う 込 こ 曲面 きょくめん 他 た 一定 いってい 平均 へいきん 曲 きょく 率 りつ 持 も 埋 う 込 こ 曲面 きょくめん 極小 きょくしょう 曲面 きょくめん
「球面 きゅうめん 正 せい 一定 いってい 曲 きょく 率 りつ 持 も [注釈 ちゅうしゃく ガウス曲 きょく 率 りつ は二 ふた 主 しゅ 曲 きょく 率 りつ 積 せき 曲 きょく 率 りつ 曲面 きょくめん 上 じょう 長 なが 角度 かくど 測 はか 決定 けってい 曲面 きょくめん 空間 くうかん 埋 う 込 こ 仕方 しかた 依 よ 意味 いみ 曲面 きょくめん 持 も 内在 ないざい 的 てき 性質 せいしつ 曲面 きょくめん 曲 ま 曲 きょく 率 りつ 変 か 正 せい 一定 いってい 曲 きょく 率 りつ 持 も 曲面 きょくめん 球面 きゅうめん 小 ちい 切 き 目 め 入 い 曲 ま 得 え 得 え 球面 きゅうめん 以外 いがい 曲線 きょくせん 境界 きょうかい 持 も 球面 きゅうめん 境界 きょうかい 持 も 正 せい 一定 いってい 曲 きょく 率 りつ 持 も 唯一 ゆいいつ 曲面 きょくめん 擬 なずらえ 球面 きゅうめん 負 まけ 一定 いってい 曲 きょく 率 りつ 持 も 曲面 きょくめん 例 れい
「剛体 ごうたい 運動 うんどう 三 さん 径 みち 数 すう 族 ぞく 球面 きゅうめん 球面 きゅうめん 自身 じしん 変形 へんけい [注釈 ちゅうしゃく 原点 げんてん 中心 ちゅうしん 単位 たんい 球面 きゅうめん 任意 にんい 座標軸 ざひょうじく 回 まわ 回転 かいてん 球面 きゅうめん 自身 じしん 写 うつ 原点 げんてん 通 とお 任意 にんい 直線 ちょくせん 周 まわ 回転 かいてん 三 さん 座標軸 ざひょうじく 周 まわ 回転 かいてん 組 く 合 あ 表 あらわ オイラー角 かく の項 こう 参照 さんしょう 先 さき 球面 きゅうめん 自身 じしん 写 うつ 任意 にんい 回転 かいてん 回転 かいてん 三 さん 径 みち 数 すう 族 ぞく 存在 そんざい 族 ぞく 三 さん 次元 じげん 回転 かいてん 群 ぐん SO (3)変換 へんかん 三 さん 径 みち 数 すう 族 ぞく 持 も 曲面 きょくめん 平面 へいめん 場合 ばあい 族 ぞく x -軸 じく y -軸 じく 沿 そ 平行 へいこう 移動 いどう 原点 げんてん 中心 ちゅうしん 回転 かいてん 径 みち 数 すう 付 つ 限 かぎ 円筒 えんとう 剛体 ごうたい 運動 うんどう 径 みち 数 すう 族 ぞく 持 も 唯一 ゆいいつ 曲面 きょくめん 一 いち 径 みち 数 すう 族 ぞく 持 も 曲面 きょくめん 回転 かいてん 曲面 きょくめん 螺旋 らせん 面 めん (英語 えいご 版 ばん 限 かぎ
An image of one of the most accurate human-made spheres, as it
refracts the image of
Einstein in the background. This sphere was a
fused quartz gyroscope for the
Gravity Probe B experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10
nanometers ) of thickness. It was announced on 1 July 2008 that
Australian scientists had created even more nearly perfect spheres, accurate to 0.3 nanometers, as part of an international hunt to find a new global standard
kilogram .
[ 14]
Deck of playing cards illustrating engineering instruments, England, 1702.
King of spades : Spheres
Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry , Dover, ISBN 978-0-486-81026-3 Dunham, William. The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities . pp. 28, 226. ISBN 0-471-17661-3 Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley , ISBN 0-471-50728-8 Steinhaus, H. (1969), Mathematical Snapshots (Third American ed.), Oxford University Press Woods, Frederick S. (1961) [1922], Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry , Dover 














![An image of one of the most accurate human-made spheres, as it refracts the image of Einstein in the background. This sphere was a fused quartz gyroscope for the Gravity Probe B experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10 nanometers) of thickness. It was announced on 1 July 2008 that Australian scientists had created even more nearly perfect spheres, accurate to 0.3 nanometers, as part of an international hunt to find a new global standard kilogram.[14]](https://upload.wikimedia.org/wikipedia/commons/thumb/9/9b/Einstein_gyro_gravity_probe_b.jpg/447px-Einstein_gyro_gravity_probe_b.jpg)
