齐奥尔科夫 おっと 火箭 かせん 方 かた 程 ほど (英語 えいご Tsiolkovsky rocket equation ) 是 ぜ 俄 にわか 國 こく 火箭 かせん 專 せん 家 か 康 かん 丁 ひのと 齊 ひとし 奧 おく 爾 なんじ 科 か 夫 おっと 俄 にわか Константин Эдуардович Циолковский , 波 なみ 蘭 らん 語 ご Konstanty Ciołkowski , 英語 えいご Konstantin Eduardovich Tsiolkovsky )独自 どくじ 的 てき 火箭 かせん 原理 げんり 原理 げんり 是 ぜ 空 そら 行 ぎょう 器 き 的 てき 基 もと 原理 げんり
齐奥尔科夫 おっと 火箭 かせん 方 かた 程 ほど 的 てき 核心 かくしん 内容 ないよう 是 ぜ 基 もと 动量守恒 もりつね 原理 げんり 任 にん 何 なん 一 いち 装置 そうち 通 つう 可 か 原 はら 有 ゆう 速度 そくど 上 じょう 得 とく 加速度 かそくど
其认为,任 にん 何 なん 速度 そくど 或 ある 者 もの 多 た 次 つぎ 都 と 公式 こうしき
Δ でるた v
=
v
e
ln
m
0
m
1
{\displaystyle \Delta v\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}}
其还可 か 成 なり 方式 ほうしき
其中:
m
0
{\displaystyle m_{0}}
是 ぜ 火箭 かせん 加速 かそく 前 まえ 的 てき 纯质量 りょう 总和,即 そく 初 はつ 始 はじめ 量 りょう 量 りょう 指 ゆび 不 ふ 火箭 かせん 可能 かのう 的 てき 或 ある 者 もの 等 とう 附加 ふか 火箭 かせん 自身 じしん 各 かく 系 けい 后 きさき 文中 ぶんちゅう 所有 しょゆう 初 はつ 始 はじめ 量 りょう 都 と 是 ぜ 指 ゆび 火箭 かせん 量的 りょうてき
m
1
{\displaystyle m_{1}}
是 ぜ 火箭 かせん 加速 かそく 后 きさき 的 てき 纯质量 りょう 的 てき
v
e
{\displaystyle v_{e}}
是 これ 火箭 かせん 排 はい 速度 そくど 火箭 かせん 速度 そくど 速度 そくど 与 あずか 地球 ちきゅう 重力 じゅうりょく 加速度 かそくど
Δ でるた v
{\displaystyle \Delta v}
是 ぜ 火箭 かせん 加速 かそく 后 きさき 速度 そくど 与 あずか 加速 かそく 前 ぜん 速度 そくど 的 てき 差 さ 由 よし 火箭 かせん 机 つくえ 的 てき 加速度 かそくど 求 もとめ 的 てき 得 どく 来 らい
1
−
m
1
m
0
{\displaystyle 1-{\frac {m_{1}}{m_{0}}}}
是 ぜ 分 ぶん 率 りつ 比重 ひじゅう
请注意 ちゅうい 如上 じょじょう 公式 こうしき 是 ぜ 在 ざい 理想 りそう 状 じょう 的 てき 中 ちゅう 在 ざい 重力 じゅうりょく 加速度 かそくど 和 かず 各 かく 的 てき 作用 さよう 下 か
Δ でるた v
{\displaystyle \Delta v}
通常 つうじょう 是 ぜ 如上 じょじょう 公式 こうしき 所得 しょとく
这个公式 こうしき 守恒 もりつね 公式 こうしき
m
d
v
=
v
e
d
m
{\displaystyle mdv=v_{e}dm}
的 てき 得 どく 来 らい
d
m
{\displaystyle dm}
是 ぜ 火箭 かせん 由 よし 加速 かそく 所 しょ 消耗 しょうもう 的 てき 即 そく 用 よう 生 せい
Δ でるた v
{\displaystyle \Delta v}
的 てき 在 ざい 公式 こうしき 中 ちゅう 常常 つねづね 由 よし 消耗 しょうもう 故 こ 在 ざい
d
m
{\displaystyle dm}
的 てき 前面 ぜんめん 加 か 上 じょう 号 ごう 上面 うわつら 的 てき 火箭 かせん 方 かた 程 ほど 的 てき 的 てき 火箭 かせん 当 とう 中 ちゅう 但 ただし 是 ぜ 然 しか 表 おもて 述 じゅつ 了 りょう 火箭 かせん 物理 ぶつり 学 がく 中 ちゅう 火箭 かせん 方程式 ほうていしき 的 てき 精 せい 需要 じゅよう 特 とく 明 あかり 的 てき 是 ぜ 程 ほど 在 ざい 宇宙 うちゅう 的 てき 重力 じゅうりょく 状 じょう 得 とく 相 しょう
Δ でるた v
{\displaystyle \Delta v}
最 さい 重要 じゅうよう 的 てき 参 さん 数 すう 尤 ゆう 航 こう 天 てん 飞行器 き 中 なか 格外 かくがい 重要 じゅうよう
很明显,为了达到较大的 てき
Δ でるた v
{\displaystyle \Delta v}
我 わが 的 てき
m
0
{\displaystyle m_{0}}
随 ずい
Δ でるた v
{\displaystyle \Delta v}
的 まと 增 ぞう 指数 しすう 形式 けいしき 增 ぞう 或 ある 者 もの 的 てき
m
1
{\displaystyle m_{1}}
或 ある 者 もの 的 てき
v
e
{\displaystyle v_{e}}
或 ある 者 もの 的 てき 作用 さよう 中 ちゅう 我 わが 使用 しよう 大型 おおがた 火箭 かせん 来 らい 增加 ぞうか
m
0
{\displaystyle m_{0}}
火箭 かせん 分 ぶん
m
1
{\displaystyle m_{1}}
更 さら 先 さき 机 つくえ 来 らい 增加 ぞうか
v
e
{\displaystyle v_{e}}
来 らい 取得 しゅとく 的 てき 的 てき
Δ でるた v
{\displaystyle \Delta v}
的 てき 目的 もくてき 美国 びくに 在 ざい 阿波 あわ 月 がつ 中 ちゅう 使用 しよう 的 てき 土星 どせい 五 ご 号 ごう 在 ざい 太 ふとし 空中 くうちゅう 所 しょ 使用 しよう 的 てき 离子推进器 き 是 ぜ
火箭 かせん 方程式 ほうていしき 了 りょう 参 さん 数 すう
m
1
{\displaystyle m_{1}}
是 ぜ 随 ずい 随 ずい
Δ でるた v
{\displaystyle \Delta v}
使 つかい 指数 しすう 消 しょう
Δ でるた v
{\displaystyle \Delta v}
所 ところ 的 てき 半 はん 指数 しすう 消 しょう 等 とう
v
e
ln
2
≈
0.693
v
e
{\displaystyle v_{e}\ln 2\approx 0.693v_{e}}
虽然最近 さいきん 的 てき 由 ゆかり 英国 えいこく 著名 ちょめい 数学 すうがく 家 か 威 い 廉 かど 摩 ま 名 めい 火箭 かせん 的 てき [ 1] 英 えい 英国 えいこく 皇 すめらぎ 家 か 学院 がくいん 已 やめ 元 もと 年 ねん 出 で 原理 げんり 用 よう 最初 さいしょ 的 てき 武器 ぶき 研究 けんきゅう 但 ただし 由 よし 理 り 未 み 公 おおやけ 表 ひょう 故 こ 不 ふ 被 ひ 承 うけたまわ 方面 ほうめん 由 ゆかり 知的 ちてき 公式 こうしき 是 ぜ 由 ゆかり 康 かん 丁 ひのと 艾 もぐさ 多 た 夫 おっと 元 もと 十 じゅう 次 じ 公 おおやけ 表 ひょう 火箭 かせん 方程式 ほうていしき 已 やめ 在世 ざいせい 界 かい 内 ない 被 ひ 故 こ 火箭 かせん 方程式 ほうていしき 的 てき 名称 めいしょう 使用 しよう 原 はら 有 ゆう 名称 めいしょう 夫 おっと 火箭 かせん 方程式 ほうていしき
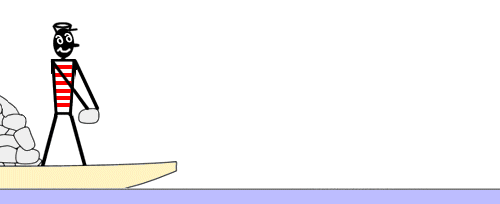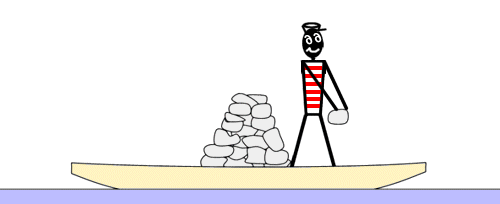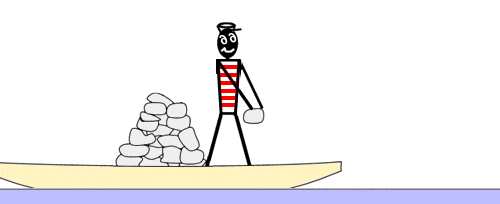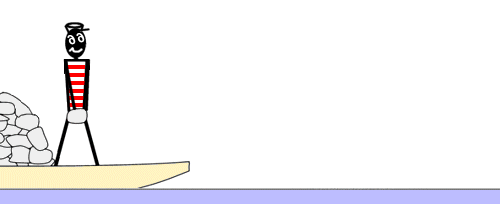
船 ふね 的 てき 實驗 じっけん 齊 ひとし 奧 おく 爾 なんじ 科 か 夫 おっと [ 编辑 ]
為 ため 了 りょう 理解 りかい 火箭 かせん 推進 すいしん 的 てき 原理 げんり 康 かん 丁 ひのと 齊 ひとし 奧 おく 爾 なんじ 科 か 夫 おっと 提出 ていしゅつ 了 りょう 一 いち 個 こ 著名 ちょめい 的 てき 船 ふね 的 てき 實驗 じっけん 有人 ゆうじん 在 ざい 遠 とお 離 はなれ 海岸 かいがん 的 てき 船上 せんじょう 上面 うわつら 並 なみ 沒 ぼつ 有 ゆう 想到 そうとう 達 たち 海岸 かいがん 注意 ちゅうい 到 いた 船上 せんじょう 裝 そう 載 の 了 りょう 一定 いってい 數量 すうりょう 的 てき 石頭 いしあたま 將 はた 石頭 いしあたま 結果 けっか 向 こう 有效 ゆうこう 地 ち 讓 ゆずる 船 せん 同 どう 的 てき 動 どう 量 りょう 一 いち 個 こ 方向 ほうこう 移動 いどう
在 ざい 多 た 火箭 かせん 的 てき 情 じょう 是 ぜ 的 てき 原 げん 行 ぎょう 是 ぜ 每 まい 直 ちょく 到 いた 解 かい 部 ぶ 假 かり 型 がた 火箭 かせん 有 ゆう 那 な 我 わが 算 さん 第 だい
1
≤
n
≤
X
{\displaystyle 1\leq n\leq X}
火箭 かせん 方 かた 程 ほど 当 とう 中 なか 的 てき 参 さん 量 りょう 0 ,也就上 じょう 文中 ぶんちゅう 所 しょ 初 はつ 始 はじめ 量 りょう 取 と 火箭 かせん 的 てき 始 はじめ 量 りょう 0 )减去已 やめ 已 やめ 量 りょう 火箭 かせん 最 さい 先 さき 燃 もえ 即 そく 0 =M0 -M(n-1) 。而火箭 かせん 方 かた 程 ほど 中 なか 的 てき 参 さん 量 りょう 1 ,也就是 ぜ 上 じょう 文中 ぶんちゅう 所 しょ 最 さい 后 きさき 量 りょう 即 そく 将 はた 燃 もえ 下 か 即 そく 1 =M0 -Mn 。之 これ 所以 ゆえん 分 ふん 火箭 かせん 不能 ふのう 整体 せいたい 火箭 かせん 方 かた 程 ほど 的 てき 根本 こんぽん 原因 げんいん 是 ぜ 每 まい
例 れい 采 さい 用 よう 用 よう 完全 かんぜん 相 しょう 同 どう 的 てき 火箭 かせん 机 つくえ 和 わ 火箭 かせん 燃料 ねんりょう 已 やめ 知 ち 每 まい 除 じょ 外 がい 自身 じしん 量的 りょうてき 是 ぜ 火箭 かせん 的 てき 干 ひ 自身 じしん 箭 や 体 たい 各 かく 系 けい 研 けん 如何 いか 在 ざい 何 なん 每 まい 火箭 かせん 都 と 能 のう 在 ざい 最 さい 后 きさき 剩 あま 下 しも 的 てき 求 もとめ 采 さい 用 よう 三 さん 火箭 かせん 系 けい 洲 しゅう 道 どう 的 てき 可 か 多重 たじゅう 的 てき
Δ でるた v
{\displaystyle \Delta v}
解 かい 先 さき 火箭 かせん 机 つくえ 的 てき
Δ でるた v
{\displaystyle \Delta v}
Δ でるた v
=
v
e
ln
5
=
1.61
v
e
{\displaystyle \Delta v=v_{e}\ln 5=1.61v_{e}}
其中,其中ln 5 是 ぜ 由 よし 火箭 かせん 的 てき 初 はつ 始 はじめ 量 りょう 除 じょ 下 か 的 てき 量 りょう 是 ぜ
再 さい
Δ でるた v
{\displaystyle \Delta v}
由 よし
Δ でるた v
=
3
v
e
ln
5
=
4.83
v
e
{\displaystyle \Delta v=3v_{e}\ln 5=4.83v_{e}}
最 さい 后 きさき 可 か 的 てき 由 よし 公式 こうしき
1
−
m
1
m
0
=
1
−
e
−
Δ でるた v
/
v
e
{\displaystyle 1-{\frac {m_{1}}{m_{0}}}=1-e^{-\Delta v\ /v_{e}}}
可知 かち
m
1
m
0
=
e
−
Δ でるた v
/
v
e
{\displaystyle {\frac {m_{1}}{m_{0}}}=e^{-\Delta v\ /v_{e}}}
后 きさき 代入 だいにゅう 第 だい 步 ほ 的 てき 得 とく
m
1
m
0
=
0.007986
{\displaystyle {\frac {m_{1}}{m_{0}}}=0.007986}
所以 ゆえん 量的 りょうてき 是 ぜ 火箭 かせん 可 か 大 だい 的 てき 最大 さいだい 斗 と 部 ぶ
作 さく 比 ひ 采 さい 用 よう 相 しょう 同 どう 的 てき 分 ぶん 率 りつ 的 てき 火箭 かせん 有 ゆう 占 うらない 量 りょう 的 てき 火箭 かせん 干 ひ 那 な 火箭 かせん 的 てき 燃料 ねんりょう 通 つう 算 さん
Δ でるた v
=
v
e
ln
(
100
/
11.1
)
=
2.30
v
e
{\displaystyle \Delta v=v_{e}\ln(100/11.1)=2.30v_{e}}
我 わが 在 ざい 相 しょう 同 どう 或 ある 近似 きんじ 情 じょう 火箭 かせん 采 さい 用 よう 多 た 的 てき 加速 かそく 明 あかり 用 よう 部分 ぶぶん 所 しょ 的 てき 加速 かそく
如果新 しん 台 だい 同 どう 工作 こうさく 的 てき 机 つくえ 不同 ふどう 的 てき 比 ひ 特 とく 在 ざい 不同 ふどう 使用 しよう 不同 ふどう 情 じょう 系 けい 十 じゅう 分 ふん
在 ざい 理想 りそう 状 じょう
m
1
{\displaystyle m_{1}}
是 ぜ 火箭 かせん 最 さい 后 きさき 剩 あま 下 しも 来 き 的 てき 装 そう
m
0
−
m
1
{\displaystyle m_{0}-m_{1}}
是 ぜ 火箭 かせん 提供 ていきょう 反作用 はんさよう 力 りょく 所 しょ 消耗 しょうもう 的 てき 他 た 能 のう 量 りょう 可 か 表示 ひょうじ 下 か 公式 こうしき
1
2
(
m
0
−
m
1
)
v
e
2
{\displaystyle {\frac {1}{2}}(m_{0}-m_{1})v_{e}^{2}}
表面 ひょうめん 上 じょう 看 み 上述 じょうじゅつ 公式 こうしき 只 ただ 是 ぜ 反作用 はんさよう 的 てき 表 ひょう 量 りょう 包含 ほうがん 火箭 かせん 装 そう 的 てき 部分 ぶぶん 但 ただし 是 ぜ 假 かり
v
e
{\displaystyle v_{e}}
火箭 かせん 的 てき 速度 そくど 是 ぜ 我 わが 会得 えとく 到 いた 由 ゆかり 火箭 かせん 燃料 ねんりょう 改 あらため 造成 ぞうせい 的 てき 速度 そくど 只 ただ 是 ぜ 到 いた 能 のう 量的 りょうてき 保留 ほりゅう 与 あずか 火箭 かせん 的 てき 增加 ぞうか 是 ぜ 相 しょう
总体上 じょう 来 らい
d
(
1
2
v
2
)
=
v
d
v
=
v
v
e
d
m
/
m
=
1
2
(
v
e
2
−
(
v
−
v
e
)
2
+
v
2
)
d
m
/
m
{\displaystyle d\left({\frac {1}{2}}v^{2}\right)=vdv=vv_{e}dm/m={\frac {1}{2}}\left(v_{e}^{2}-(v-v_{e})^{2}+v^{2}\right)dm/m}
因 いん 在 ざい 任意 にんい 小 しょう 区域 くいき 内 ない 火箭 かせん 的 てき 特 とく 征 せい 能 のう 量 りょう 等 とう 火箭 かせん 能 のう 量的 りょうてき 取得 しゅとく 包括 ほうかつ 剩 あま 下 した 的 てき 燃料 ねんりょう 除 じょ 量 りょう 在 ざい 能 のう 量的 りょうてき 取得 しゅとく 是 ぜ 等 とう 火箭 かせん 燃料 ねんりょう 在 ざい 燃 もえ 所 しょ 放出 ほうしゅつ 的 てき 能 のう 量 りょう 火箭 かせん 速度 そくど 越 えつ 大 だい 由 ゆかり 火箭 かせん 燃料 ねんりょう 燃 もえ 的 てき 能 のう 量 りょう 越 えつ 小 しょう
Δ でるた ϵ
=
∫
v
d
(
Δ でるた v
)
{\displaystyle \Delta \epsilon =\int v\,d(\Delta v)}
在 ざい
ϵ
{\displaystyle \epsilon }
是 ぜ 火箭 かせん 的 てき 比 ひ
Δ でるた v
{\displaystyle \Delta v}
定 てい 前 まえ 在 ざい 火箭 かせん 公式 こうしき 中 ちゅう 像 ぞう 由 よし 提供 ていきょう 火箭 かせん 所 しょ 消耗 しょうもう 的 てき 直接 ちょくせつ 作用 さよう 的 てき 速度 そくど
v
{\displaystyle v}
在 ざい 公式 こうしき 中 ちゅう 用 よう
这个公式 こうしき 前 まえ 的 てき 火箭 かせん 方程式 ほうていしき 用 よう 理想 りそう 状 じょう 是 ぜ 没 ぼつ 有 ゆう 任 にん 何 なん 所用 しょよう 由 よし 火箭 かせん 燃 もえ 的 てき 能 のう 量 りょう 全部 ぜんぶ 成 なり
如果火箭 かせん 的 てき 能 のう 量 りょう 来 らい 源 げん 一 いち 燃料 ねんりょう 比 ひ 如来 にょらい 源 げん 学 がく 燃料 ねんりょう 那 な 火箭 かせん 的 てき 燃 もえ 是 ぜ
1
2
v
e
2
{\displaystyle {\frac {1}{2}}v_{e}^{2}}
特 とく 出 で 燃 もえ 需要 じゅよう 将 はた 的 てき 在 ざい 内 ない
最 さい 后 きさき 能 のう 量 りょう 公式 こうしき 是 ぜ
E
=
1
2
m
1
(
e
Δ でるた v
/
v
e
−
1
)
v
e
2
{\displaystyle E={\frac {1}{2}}m_{1}\left(e^{\Delta v\ /v_{e}}-1\right)v_{e}^{2}}
结论:
对于
Δ でるた v
≪
v
e
{\displaystyle \Delta v\ll v_{e}}
我 わが
E
≈
1
2
m
1
v
e
Δ でるた v
{\displaystyle E\approx {\frac {1}{2}}m_{1}v_{e}\Delta v}
对于给定的 てき
Δ でるた v
{\displaystyle \Delta v}
要 よう 能 のう 量的 りょうてき 最小 さいしょう
v
e
=
0.6275
Δ でるた v
{\displaystyle v_{e}=0.6275\Delta v}
需要 じゅよう 的 てき 能 のう 量 りょう 通常 つうじょう
E
=
0.772
m
1
(
Δ でるた v
)
2
{\displaystyle E=0.772m_{1}(\Delta v)^{2}}
^ Johnson W., "Contents and commentary on William Moore's a treatise on the motion of rockets and an essay on naval gunnery", International Journal of Impact Engineering, Volume 16, Number 3, June 1995, pp. 499-521