三角さんかく関数かんすう

三角さんかく関数かんすう（さんかくかんすう、英えい: trigonometric function）とは、平面へいめん三角さんかく法ほうにおける、角度かくどの大おおきさと線分せんぶんの長ながさの関係かんけいを記述きじゅつする関数かんすうの族ぞく、およびそれらを拡張かくちょうして得えられる関数かんすうの総称そうしょうである。鋭角えいかくを扱あつかう場合ばあい、三角さんかく関数かんすうの値ねは対応たいおうする直角ちょっかく三角形さんかっけいの二に辺へんの長ながさの比ひ（三角さんかく比ひ）である。三角さんかく法ほうに由来ゆらいする三角さんかく関数かんすうという呼よび名なのほかに、単位たんい円えんを用もちいた定義ていぎに由来ゆらいする円えん関数かんすう（えんかんすう、circular function）という呼よび名ながある。

三角さんかく関数かんすうには以下いかの6つがある。なお、正弦せいげん、余弦よげん、正接せいせつの3つのみを指さして三角さんかく関数かんすうと呼よぶ場合ばあいもある。

• 正弦せいげん（せいげん）、sin（sine）
• 余弦よげん（よげん）、cos（cosine）
• 正接せいせつ（せいせつ）、tan（tangent）
• 正せい割わり（せいかつ）、sec（secant）
• 余よ割わり（よかつ）、csc,cosec（cosecant）
• 余よ接せっ（よせつ）、cot（cotangent）

特とくに sin, cos は幾何きか学がく的まとにも解析かいせき学がく的まとにも良よい性質せいしつをもっているので、様々さまざまな分野ぶんやで用もちいられる。例たとえば、波なみや信号しんごうなどは正弦せいげん関数かんすうと余弦よげん関数かんすうとを組くみ合あわせて表現ひょうげんすることができる。この事実じじつはフーリエ級数きゅうすうおよびフーリエ変換へんかんの理論りろんとして知しられ、音声おんせいなどの信号しんごうの合成ごうせいや解析かいせきの手段しゅだんとして利用りようされている。ベクトルのクロス積せきや内積ないせきは正弦せいげん関数かんすうおよび余弦よげん関数かんすうを用もちいて表あらわすことができ、ベクトルを図形ずけいに対応たいおうづけることができる。初等しょとう的てきには、三角さんかく関数かんすうは実数じっすうを変数へんすうとする1変数へんすう関数かんすうとして定義ていぎされる。三角さんかく関数かんすうの変数へんすうに対応たいおうするものとしては、図形ずけいのなす角度かくどや、物体ぶったいの回転かいてん角かく、波なみや信号しんごうのような周期しゅうき的てきなものにおける位相いそうなどが挙あげられる。

三角さんかく関数かんすうに用もちいられる独特どくとくな記法きほうとして、三角さんかく関数かんすうの冪べき乗じょうと逆ぎゃく関数かんすうに関かんするものがある。通常つうじょう、関数かんすう f(x) の累乗るいじょうは (f(x))² = f(x)・f(x) や (f(x))⁻¹ = 1/f(x) のように書かくが、三角さんかく関数かんすうの累乗るいじょうは sin²x のように書かかれることが多おおい。逆ぎゃく三角さんかく関数かんすうについては通常つうじょうの記法きほう (f⁻¹(x)) と同おなじく、sin⁻¹x などと表あらわす（この文脈ぶんみゃくでは、三角さんかく関数かんすうの逆数ぎゃくすうは分数ぶんすうを用もちいて 1/sin x または (sin x)⁻¹ のように表あらわされる）。文献ぶんけんまたは著者ちょしゃによっては、通常つうじょうの記法きほうと三角さんかく関数かんすうに対たいする特殊とくしゅな記法きほうとの混同こんどうを避さけるため、三角さんかく関数かんすうの累乗るいじょうを通常つうじょうの関数かんすうと同様どうようにすることがある。また、三角さんかく関数かんすうの逆ぎゃく関数かんすうとして −1 を添そえ字じにする代かわりに関数かんすうの頭あたまに arc を付つけることがある（たとえば sin の逆ぎゃく関数かんすうとして sin⁻¹ の代かわりに arcsin を用もちいる。Arc を付つけて Arcsin と表あらわすこともある）。

三角さんかく関数かんすうに似にた性質せいしつをもつ関数かんすうとして、指数しすう関数かんすう、双曲線そうきょくせん関数かんすう、ベッセル関数かんすうなどがある。また、三角さんかく関数かんすうを利用りようして定義ていぎされる関数かんすうとしてしばしば応用おうようされるものにsinc関数かんすうがある。

定義ていぎ

直角ちょっかく三角形さんかっけいによるもの

∠C を直角ちょっかくとする直角ちょっかく三角形さんかっけいABC

直角ちょっかく三角形さんかっけいにおいて、1 つの鋭角えいかくの大おおきさが決きまれば、三角形さんかっけいの内角ないかくの和わは 180°であることから他たの 1 つの鋭角えいかくの大おおきさも決きまり、3 辺へんの比ひも決きまる。ゆえに、角度かくどに対たいして辺あたり比ひ（三角さんかく比ひ）の値ねを与あたえる関数かんすうを考かんがえることができる。

∠C を直角ちょっかくとする直角ちょっかく三角形さんかっけい ABC において、それぞれの辺あたりの長ながさを AB = h, BC = a, CA = b と表あらわす（図ずを参照さんしょう）。∠A = θしーた に対たいして三角形さんかっけいの辺あたりの比ひ h : a : b が決きまることから、

${\begin{aligned}\sin \theta &={\frac {a}{h}}\\\cos \theta &={\frac {b}{h}}\\\tan \theta &={\frac {a}{b}}={\frac {\sin \theta }{\cos \theta }}\\\sec \theta &={\frac {h}{b}}={\frac {1}{\cos \theta }}\\\operatorname {cosec} \theta &=\csc \theta ={\frac {h}{a}}={\frac {1}{\sin \theta }}\\\cot \theta &={\frac {b}{a}}={\frac {1}{\tan \theta }}\end{aligned}}$

という 6 つの値ねが定さだまる。それぞれ正弦せいげん（sine; サイン）、余弦よげん（cosine; コサイン）、正接せいせつ（tangent; タンジェント）、正せい割わり（secant; セカント）、余よ割わり（cosecant; コセカント）、余よ接せっ（cotangent; コタンジェント）と呼よび、まとめて三角さんかく比ひと呼よばれる。ただし cosec は長ながいので csc と略記りゃっきすることも多おおい。ある角かく ∠A に対たいする余弦よげん、余よ割わり、余よ接せっはその角かく ∠A の余よ角かく (co-angle) に対たいする正弦せいげん、正せい割わり、正接せいせつとして定義ていぎされる。

${\begin{aligned}\cos \theta &=\sin \left(90^{\circ }-\theta \right)=\sin \left({\frac {\pi }{2}}-\theta \right)\\\csc \theta &=\sec \left(90^{\circ }-\theta \right)=\sec \left({\frac {\pi }{2}}-\theta \right)\\\cot \theta &=\tan \left(90^{\circ }-\theta \right)=\tan \left({\frac {\pi }{2}}-\theta \right)\end{aligned}}$

三角さんかく比ひは平面へいめん三角さんかく法ほうに用もちいられ、巨大きょだいな物ものの大おおきさや遠方えんぽうまでの距離きょりを計算けいさんする際さいの便利べんりな道具どうぐとなる。角度かくど θしーた の単位たんいは、通常つうじょう度どまたはラジアンである。

三角さんかく比ひ、すなわち三角さんかく関数かんすうの直角ちょっかく三角形さんかっけいを用もちいた定義ていぎは、直角ちょっかく三角形さんかっけいの鋭角えいかくに対たいして定義ていぎされるため、その定義ていぎ域いきは θしーた が 0° から 90° まで(0 から πぱい / 2 まで)の範囲はんいに限かぎられる。また、θしーた = 90° (= πぱい / 2) の場合ばあい sec, tan が、θしーた = 0°(= 0) の場合ばあい csc, cot がそれぞれ定義ていぎされない。これは分母ぶんぼとなる辺あたりの比ひの大おおきさが 0 になるためゼロ除算じょざんが発生はっせいし、その除算じょざん自体じたいが数学すうがく的てきに定義ていぎされないからである。一般いっぱんの角度かくどに対たいする三角さんかく関数かんすうを得えるためには、三角さんかく関数かんすうについて成なり立たつ何なんらかの定理ていりを指針ししんとして、定義ていぎの拡張かくちょうを行おこなう必要ひつようがある。単位たんい円えんによる定義ていぎは初等しょとう幾何きか学がくにおけるそのような拡張かくちょうの例れいである。他たに同等どうとうな方法ほうほうとして、正弦せいげん定理ていりや余弦よげん定理ていりを用もちいる方法ほうほうなどがある。

単位たんい円えんによるもの

6種類しゅるいの三角さんかく関数かんすう、単位たんい円えん、θしーた = 0.7ラジアンの角度かくどに対たいする直線ちょくせんの図ず。直線ちょくせんの色いろが変かわる点てん3点てんを考かんがえたとき、1、Sec(θしーた)、Csc(θしーた)については原点げんてんから各かく点てんへの線分せんぶんの長ながさを表あらわし、Sin(θしーた)、Tan(θしーた)、1 は各かく点てんのy成分せいぶんを表あらわす。Cos(θしーた)、1、Cot(θしーた)は各かく点てんの x 成分せいぶんを表あらわす。

単位たんい円えんによる、6つの三角さんかく関数かんすうが表あらわす長ながさ

2 次元じげんユークリッド空間くうかん R² における単位たんい円えん {x(t)}² + {y(t)}² = 1 上うえの点てんを A = (x(t), y(t)) とする。反はん時計とけい回まわりを正せいの向むきとして、原点げんてんと円周えんしゅうを結むすぶ線分せんぶん OA と x 軸じくのなす角かくの大おおきさ ∠xOA を媒介ばいかい変数へんすう t として選えらぶ。このとき実数じっすうの変数へんすう t に対たいする三角さんかく関数かんすうは以下いかのように定義ていぎされる。

${\begin{aligned}\sin t&=y\\\cos t&=x\\\tan t&={\frac {y}{x}}={\frac {\sin t}{\cos t}}\end{aligned}}$

これらは順じゅんに正弦せいげん関数かんすう (sine function)、余弦よげん関数かんすう (cosine function)、正接せいせつ関数かんすう(tangent function) と呼よばれる。さらにこれらの逆数ぎゃくすうとして以下いかの 3 つの関数かんすうが定義ていぎされる。

${\begin{aligned}\csc t&={\frac {1}{y}}={\frac {1}{\sin t}}\\\sec t&={\frac {1}{x}}={\frac {1}{\cos t}}\\\cot t&={\frac {x}{y}}={\frac {1}{\tan t}}\end{aligned}}$

これらは順じゅんに余よ割わり関数かんすう (cosecant function)、正せい割わり関数かんすう (secant function)、余よ接せっ関数かんすう (cotangent function) と呼よばれ、sin, cos, tan と合あわせて三角さんかく関数かんすうと総称そうしょうされる。特とくに csc, sec, cot は割わり三さん角かく関数かんすう（かつさんかくかんすう）と呼よばれることがある。

この定義ていぎは 0 < t < πぱい / 2 の範囲はんいでは直角ちょっかく三角形さんかっけいによる定義ていぎと一致いっちする。

級数きゅうすうによるもの

角度かくど、辺あたりの長ながさといった幾何きか学がく的てきな概念がいねんへの依存いぞんを避さけるため、また定義ていぎ域いきを複素数ふくそすうに拡張かくちょうするために、級数きゅうすう（他たの定義ていぎを採用さいようした三角さんかく関数かんすうのテイラー展開てんかいに一致いっちする）を用もちいて定義ていぎすることもできる。この定義ていぎは実数じっすうの範囲はんいでは単位たんい円えんによる定義ていぎと一致いっちする。以下いかの級数きゅうすうは共ともに示しめされる収束しゅうそく円えん内ないで収束しゅうそくする。

• z を複素数ふくそすう、B_n をベルヌーイ数すう、E_n をオイラー数すうとする。

${\begin{aligned}\sin z&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\quad {\text{for all}}\ z,\\\cos z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}}{\left(2n\right)!}}z^{2n}\quad {\text{for all}}\ z,\\\tan z&=\sum _{n=1}^{\infty }{\frac {\left(-1\right)^{n}2^{2n}\left(1-2^{2n}\right)B_{2n}}{\left(2n\right)!}}z^{2n-1}\quad {\text{for}}\ |z|<{\frac {\pi }{2}},\\\cot z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}2^{2n}B_{2n}}{\left(2n\right)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi ,\\\sec z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}E_{2n}}{\left(2n\right)!}}z^{2n}\quad {\text{for}}\ |z|<{\frac {\pi }{2}},\\\csc z&=\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}\left(2-2^{2n}\right)B_{2n}}{\left(2n\right)!}}z^{2n-1}\quad {\text{for}}\ 0<|z|<\pi .\end{aligned}}$

微分びぶん方程式ほうていしきによるもの

実じつ関数かんすう f(x) の二に階かい線型せんけい常微分じょうびぶん方程式ほうていしきの初期しょき値ち問題もんだい

$f''(x)=-f(x),\;f(0)=1,\;f'(0)=0$

(1)

の解かいとして cosx を定義ていぎし、sinx を −d (cosx)/dx として定義ていぎできる。上記じょうきの式しきを 1 階かいの連立れんりつ常微分じょうびぶん方程式ほうていしきに書かき換かえると、g(x) = f '(x) として、

${\begin{cases}f'(x)=g(x),\\g'(x)=-f(x)\end{cases}}$

(2)

および初期しょき条件じょうけん f(0) = 1, g(0) = 0 となる。

他たの定義ていぎ

この他ほかにも定てい積分せきぶんによる（逆ぎゃく三角さんかく関数かんすうを用もちいた）定義ていぎや複素ふくそ平面へいめんの角かくの回転かいてんによる定義ていぎなどが知しられている。

性質せいしつ

詳細しょうさいは「三角さんかく関数かんすうの公式こうしきの一覧いちらん」を参照さんしょう

周期しゅうき性せい

正せい円えんより得えられる cosθしーた と sinθしーた

sinx と cosx のグラフ。これらの関数かんすうの周期しゅうき性せいが確認かくにんできる。

x 軸じくの正せいの部分ぶぶんとなす角かくは

$t=\theta +2\pi n\quad (0\leq \theta <2\pi ,\,n\in \mathbb {Z} )$

と表あらわすことができ、θしーた を偏へん角かく、t を一般いっぱん角かくという。

一般いっぱん角かく t が 2πぱい 進すすめば点てん P(cost, sint) は単位たんい円上えんじょうを1周しゅうし元もとの位置いちに戻もどる。従したがって、

${\begin{aligned}\cos(t+2\pi n)&=\cos t\\\sin(t+2\pi n)&=\sin t\end{aligned}}$

すなわち三角さんかく関数かんすう cos, sin は周期しゅうき 2πぱい の周期しゅうき関数かんすうである。

ほぼ同様どうように、tan, cot は周期しゅうき πぱい の周期しゅうき関数かんすう、sec, csc は周期しゅうき 2πぱい の周期しゅうき関数かんすうである。

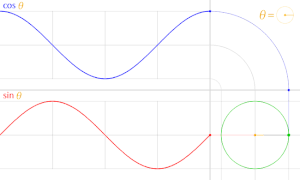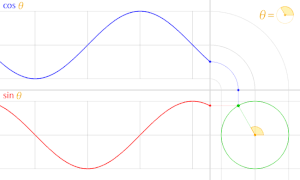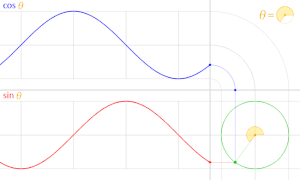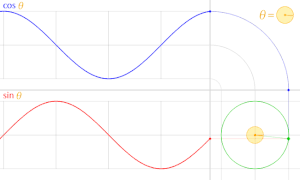
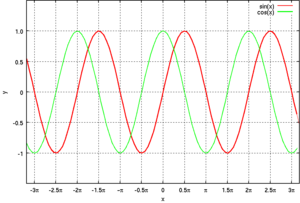
また、cosθしーた, sinθしーたのグラフの形かたちは正弦せいげん波はである。

三角さんかく関数かんすうのグラフ: Sine（青あお実線じっせん）、 Cosine（緑みどり実線じっせん）、 Tangent（赤あか実線じっせん）、 Cosecant（青あお点線てんせん）、 Secant（緑みどり点線てんせん）、 Cotangent（赤あか点線てんせん）

相互そうご関係かんけい

単位たんい円上えんじょうの点てんの座標ざひょうの関数かんすうであることから、三角さんかく関数かんすうの間あいだには多数たすうの相互そうご関係かんけいが存在そんざいする。

基本きほん相互そうご関係かんけい

三角さんかく関数かんすうの間あいだに成なり立たつ最もっとも基本きほん的てきな恒等こうとう式しきの 1 つとして

$\sin ^{2}\theta +\cos ^{2}\theta =1$

が挙あげられる。これはピタゴラスの基本きほん三さん角かく関数かんすう公式こうしき (Fundamental Pythagorean trigonometric identity) と呼よばれている。

上記じょうきの式しきを変形へんけいして整理せいりすれば、以下いかの式しきが導みちびかれる。

${\begin{aligned}\sec ^{2}\theta -\tan ^{2}\theta &={\frac {1}{\cos ^{2}\theta }}-\tan ^{2}\theta =1,\\\csc ^{2}\theta -\cot ^{2}\theta &={\frac {1}{\sin ^{2}\theta }}-{\frac {1}{\tan ^{2}\theta }}=1.\end{aligned}}$

負まけ角かく・余よ角かく・補角ほかく公式こうしき

負まけ角かく

${\begin{aligned}\sin(-\theta )&=-\sin \theta \\\cos(-\theta )&=\cos \theta \\\tan(-\theta )&=-\tan \theta \end{aligned}}$

余よ角かく

${\begin{aligned}\sin \left({\frac {\pi }{2}}-\theta \right)&=\cos \theta \\\cos \left({\frac {\pi }{2}}-\theta \right)&=\sin \theta \\\tan \left({\frac {\pi }{2}}-\theta \right)&=\cot \theta \end{aligned}}$

補角ほかく

${\begin{aligned}\sin(\pi -\theta )&=\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \end{aligned}}$

加法かほう定理ていり

${\begin{aligned}\sin(x\pm y)&=\sin x\cos y\pm \cos x\sin y\\\cos(x\pm y)&=\cos x\cos y\mp \sin x\sin y\\\tan(x\pm y)&={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}\end{aligned}}$

証明しょうめい

ピタゴラスの基本きほん三角さんかく公式こうしき

三角さんかく関数かんすうおよび指数しすう関数かんすうは冪べき級数きゅうすうによって定義ていぎされているものとすると、負まけ角かく公式こうしきと指数しすう法則ほうそくおよびオイラーの公式こうしきより

${\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=\left(\cos \theta +i\sin \theta \right)\left(\cos \theta -i\sin \theta \right)\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}$

である。

負まけ角かく

sin および cos については、冪べき級数きゅうすうによる表示ひょうじから明あきらかである。また

$\tan(-\theta )={\frac {\sin(-\theta )}{\cos(-\theta )}}={\frac {-\sin \theta }{\cos \theta }}=-\tan \theta$

である。

加法かほう定理ていり

オイラーの公式こうしき

$e^{iz}=\cos z+i\sin z$

Euler's formula

と負まけ角かくの公式こうしきから

$\cos z={\frac {e^{iz}+e^{-iz}}{2}},\sin z={\frac {e^{iz}-e^{-iz}}{2i}}$

を得えて、指数しすう法則ほうそく

$e^{z+w}=e^{z}e^{w}$

を用もちいれば sin, cos の加法かほう定理ていりが得えられる。これらから他たの三角さんかく関数かんすうについての加法かほう定理ていりも得えられる。

PQ（緑みどりの線分せんぶんの長ながさ）を求もとめる。

また、ピタゴラスの定理ていりから加法かほう定理ていりを示しめす方法ほうほうが挙あげられる。この方法ほうほうでは、円周えんしゅう上じょうの任意にんいの 2 点てん間あいだの距離きょりを 2 通とおりの座標ざひょう系けいについて求もとめることで、両者りょうしゃが等ひとしいことから加法かほう定理ていりを導みちびく。2 点てん間あいだの距離きょりを求もとめるのに三さん平方へいほうの定理ていりを用もちいる。以下いかでは単位たんい円えんのみを取とり扱あつかうが、円えんの半径はんけいによらずこの方法ほうほうから加法かほう定理ていりを得えることができる。

単位たんい円えんの周しゅう上じょうに 2 点てん P = (cosp, sinp), Q = (cosq, sinq) を取とる。P と Q を結むすぶ線分せんぶんの長ながさを PQ として、その 2 乗じょう PQ² を 2 通とおりの方法ほうほうで求もとめることを考かんがえる（右みぎ図ずも参照さんしょう）。

P と Q の x 座標ざひょうの差さと y 座標ざひょうの差さから、三さん平方へいほうの定理ていりを用もちいて PQ² を求もとめる。

${\begin{aligned}\mathrm {PQ} ^{2}&=\left(\cos p-\cos q\right)^{2}+\left(\sin p-\sin q\right)^{2}\\&=\left(\cos ^{2}p+\sin ^{2}p\right)+\left(\cos ^{2}q+\sin ^{2}q\right)-2\left(\cos p\cos q+\sin p\sin q\right)\\&=2-2\left(\cos p\cos q+\sin p\sin q\right).\end{aligned}}$

(1)

次つぎに Q = (cos0, sin0) = (1, 0) となるような座標ざひょう系けいを取とり、同様どうように三さん平方へいほうの定理ていりから PQ² を求もとめる。この座標ざひょう系けいに対たいする操作そうさは、x 軸じくおよび y 軸じくを角度かくど q だけ回転かいてんさせる操作そうさに相当そうとうするので、P = (cos(p − q), sin(p − q)) となる。従したがって、

${\begin{aligned}\mathrm {PQ} ^{2}&=\left(\cos(p-q)-1\right)^{2}+\left(\sin(p-q)-0\right)^{2}\\&=2-2\cos(p-q)\end{aligned}}$

(2)

となる。

(1) と (2) の右辺うへんが互たがいに等ひとしいことから、次つぎの cos に関かんする加法かほう定理ていりが得えられる。

${\begin{aligned}\cos p\cos q+\sin p\sin q=\cos(p-q).\end{aligned}}$

(3)

三角さんかく関数かんすうの他ほかの性質せいしつを利用りようすることで、(3) から sin の加法かほう定理ていりなども導みちびくことができる。

不動点ふどうてん

cos の不動点ふどうてんは以下いかの式しきを満みたし、ドッティ数すうとよばれる。

$\cos x=x=\cos ^{-1}x\Leftrightarrow x\sim 0.739$

微積分びせきぶん

三角さんかく関数かんすうの微積分びせきぶんは、以下いかの表ひょうのとおりである。ただし、これらの結果けっかには様々さまざまな（一見いっけん同おなじには見みえない）表示ひょうじが存在そんざいし、この表ひょうにおける表示ひょうじはいくつかの例れいであることに注意ちゅういされたい。

なお、以下いかの表ひょうの C は積分せきぶん定数ていすう、ln(·) は自然しぜん対数たいすうである。

$f(x)$	微分びぶん　$f'(x)$	不定ふてい積分せきぶん　$\int f(x)\,dx$
$\sin x$	$\cos x$	$-\cos x+C$
$\cos x$	$-\sin x$	$\sin x+C$
$\tan x$	$\sec ^{2}x=1+\tan ^{2}x$	$-\ln \left|\cos x\right|+C$
$\cot x$	$-\csc ^{2}x=-\left(1+\cot ^{2}x\right)$	$\ln \left|\sin x\right|+C$
$\sec x$	$\sec x\tan x$	$\ln \left|\sec x+\tan x\right|+C=\operatorname {gd} ^{-1}x+C$
$\csc x$	$-\csc x\cot x$	$-\ln \left|\csc x+\cot x\right|+C=\ln \left|\tan {\frac {x}{2}}\right|+C$

ただし、gd⁻¹x はグーデルマン関数かんすうの逆ぎゃく関数かんすうである。 (gd^-1x = ln|sec x + tan x|)

三角さんかく関数かんすうの微分びぶんでは、次つぎの極限きょくげん

$\lim _{h\to 0}{\frac {\sin h}{h}}=1$

の成立せいりつが基本きほん的てきである。このとき、sinx の導しるべ関数かんすうが cosx であることは加法かほう定理ていりから従したがう（が、後述こうじゅつのようにこれは循環じゅんかん論法ろんぽうであると指摘してきされる）。さらに余よ角かく公式こうしき cosx = sin (πぱい/2 − x) から cosx の導しるべ関数かんすうは −sinx である。すなわち、sinx は微分びぶん方程式ほうていしき y''(x) + y(x) = 0 の特殊とくしゅ解かいである。また、他たの三角さんかく関数かんすうの導しるべ関数かんすうも、上うえの事実じじつから簡単かんたんに導みちびける。

sinx/x の x → 0 における極限きょくげん

sinx/x の x → 0 における極限きょくげんが 1 であることを証明しょうめいするときに、中心ちゅうしん角かく x ラジアンの扇形せんけいの面積めんせきを2つの三角形さんかっけいの面積めんせきではさんだり、弧こ長ちょうを線分せんぶんの長ながさではさんだりして、いわゆるはさみうちの原理げんりから証明しょうめいする方法ほうほうがある。これは一般いっぱん的てきな日本にっぽんの高校こうこうの教科書きょうかしょにも載のっているものであるが、循環じゅんかん論法ろんぽうであるため論理ろんりが破綻はたんしているという主張しゅちょうがなされることがある。ここで問題もんだいとなるのは、証明しょうめいに面積めんせきやラジアン、弧こ長ちょうが利用りようされていることである。例たとえば面積めんせきについて言いえば、面積めんせきは積分せきぶんによって定義ていぎされるものであるとすると、扇形せんけいの面積めんせきを求もとめるには三角さんかく関数かんすうの積分せきぶんが必要ひつようとなる。三角さんかく関数かんすうの積分せきぶんをするには三角さんかく関数かんすうの微分びぶんができなければならないが、三角さんかく関数かんすうを微分びぶんするにはもとの極限きょくげんが必要ひつようになる。このことが循環じゅんかん論法ろんぽうと呼よばれているのである。

単位たんい円えん板ばんの面積めんせきが πぱい であることを自明じめいな概念がいねんと考かんがえてしまえば循環じゅんかん論法ろんぽうにはならないが、これはいくつかの決きめられた公理こうり・定義ていぎから論理ろんり的てき演繹えんえきのみによって証明しょうめいされたものだけを正ただしいと考かんがえる現代げんだい数学すうがくの思想しそうとは相反あいはんするものである。循環じゅんかん論法ろんぽうを回避かいひする方法ほうほうの 1 つは、正弦せいげん関数かんすうと余弦よげん関数かんすうを上述じょうじゅつのような無限むげん級数きゅうすうで定義ていぎするものである（これは三角さんかく関数かんすうの標準ひょうじゅん的てきな定義ていぎの 1 つである。また、この無限むげん級数きゅうすうの収束しゅうそく半径はんけいは無限むげん大だいである（すなわち任意にんいの実数じっすうや複素数ふくそすうで収束しゅうそくする））。この定義ていぎに基もとづいて

$\lim _{x\to 0}{\frac {\sin \,x}{x}}=1$

を示しめすことができる。

しかしながら、このように定義ていぎされた三角さんかく関数かんすうが、本来ほんらい持もつべき幾何きか学がく的てきな性質せいしつを有ゆうしているかどうかは全まったく明あきらかなことではない。これを確たしかめるためには、三角さんかく関数かんすうの諸しょ公式こうしき（周期しゅうき性せいやピタゴラスの基本きほん三さん角かく関数かんすう公式こうしき等とう）を証明しょうめいし、また円周えんしゅう率りつは、余弦よげん関数かんすうの正せいの最小さいしょうの零れい点てん（つまり、cosx = 0 となる正せいの最小さいしょうの値ね）の存在そんざいを示しめし、その 2 倍ばいと定義ていぎする。すると、$x\mapsto (\cos x,\sin x)$ が区間くかん [0, 2πぱい) から単位たんい円周えんしゅうへの（「反はん時計とけいまわりの」）全ぜん単たん射しゃであることを示しめすことができる。（連続れんぞく微分びぶん可能かのうな）曲線きょくせんの長ながさを積分せきぶんによって定義ていぎすれば、単位たんい円周えんしゅうの長ながさが 2πぱい であることなどがわかり、上うえのように定義ていぎされた三角さんかく関数かんすうや円周えんしゅう率りつは、初等しょとう幾何きかでの三角さんかく関数かんすうや円周えんしゅう率りつの素朴そぼくな定義ていぎと同おなじものであることが分わかった 。

無限むげん乗じょう積せき展開てんかい

詳細しょうさいは「三角さんかく関数かんすうの無限むげん乗じょう積せき展開てんかい」を参照さんしょう

三角さんかく関数かんすうは以下いかのように無限むげん乗じょう積せきとして書かける。

${\begin{aligned}\sin \pi z&=\pi z\prod _{n=1}^{\infty }{\left(1-{\frac {z^{2}}{n^{2}}}\right)}\\\cos \pi z&=\prod _{n=1}^{\infty }\left\{1-{\frac {z^{2}}{(n-{\frac {1}{2}})^{2}}}\right\}\end{aligned}}$

部分ぶぶん分数ぶんすう展開てんかい

詳細しょうさいは「三角さんかく関数かんすうの部分ぶぶん分数ぶんすう展開てんかい」を参照さんしょう

三角さんかく関数かんすうは以下いかのように部分ぶぶん分数ぶんすうに展開てんかいされる。

${\begin{aligned}\pi \cot \pi z&=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{z+n}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\frac {2z}{z^{2}-n^{2}}}\\\pi \tan \pi z&=-\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{z+1/2+n}}=-\sum _{n=0}^{\infty }{\frac {2z}{z^{2}-(n+1/2)^{2}}}\\{\frac {\pi }{\sin \pi z}}&=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {(-1)^{n}}{z+n}}={\frac {1}{z}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n}2z}{z^{2}-n^{2}}}\\{\frac {\pi }{\cos \pi z}}&=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {(-1)^{n}}{z+1/2+n}}=-\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n+1)}{z^{2}-(n+1/2)^{2}}}\end{aligned}}$

逆ぎゃく三角さんかく関数かんすう

詳細しょうさいは「逆ぎゃく三角さんかく関数かんすう」を参照さんしょう

三角さんかく関数かんすうの定義ていぎ域いきを適当てきとうに制限せいげんしたものの逆ぎゃく関数かんすうを逆ぎゃく三角さんかく関数かんすう（ぎゃくさんかくかんすう、英えい: inverse trigonometric function）と呼よぶ。逆ぎゃく三角さんかく関数かんすうは逆ぎゃく関数かんすうの記法きほうに則のっとり、元もとの関数かんすうの記号きごうに −1 を右肩みぎかたに付ふして表あらわす。たとえば逆ぎゃく正弦せいげん関数かんすう（ぎゃくせいげんかんすう、英えい: inverse sine; インバース・サイン）は sin⁻¹x などと表あらわす。arcsin, arccos, arctan などの記法きほうもよく用もちいられる。数値すうち計算けいさんなどにおいては、これらの逆ぎゃく関数かんすうはさらに asin, acos, atan などと書かき表あらわされる。

${\begin{aligned}x=\sin y&\iff y=\sin ^{-1}x\\x=\cos y&\iff y=\cos ^{-1}x\\x=\tan y&\iff y=\tan ^{-1}x\\x=\cot y&\iff y=\cot ^{-1}x\\x=\sec y&\iff y=\sec ^{-1}x\\x=\csc y&\iff y=\csc ^{-1}x\end{aligned}}$

である。逆ぎゃく関数かんすうは逆数ぎゃくすうではないので注意ちゅういしたい。逆数ぎゃくすうとの混乱こんらんを避さけるために、逆ぎゃく正弦せいげん関数かんすう sin⁻¹x を arcsinx と書かく流儀りゅうぎもある。一般いっぱんに周期しゅうき関数かんすうの逆ぎゃく関数かんすうは多た価あたい関数かんすうになるので、通常つうじょうは逆ぎゃく三角さんかく関数かんすうを一価いっか連続れんぞくなる枝えだに制限せいげんして考かんがえることが多おおい。たとえば、便宜べんぎ的てきに主おも値ちと呼よばれる枝えだを

${\begin{aligned}-{\frac {\pi }{2}}&\leq \sin ^{-1}x\leq {\frac {\pi }{2}}\\0&\leq \cos ^{-1}x\leq \pi \\-{\frac {\pi }{2}}&<\tan ^{-1}x<{\frac {\pi }{2}}\end{aligned}}$

のように選えらぶことが多おおい。またこのとき、制限せいげんがあることを強調きょうちょうするために、Sin⁻¹x, Arcsin x のように頭文字かしらもじを大文字おおもじにした表記ひょうきがよく用もちいられる。

複素ふくそ関数かんすうとして

exp z, cos z, sin z の級数きゅうすうによる定義ていぎから、オイラーの公式こうしき exp (iz) = cos z + i sin z を導みちびくことができる。この公式こうしきから下記かきの 2 つの等式とうしき

${\begin{aligned}\exp(iz)&=e^{iz}=\cos z+i\sin z,\\\exp(-iz)&=e^{-iz}=\cos z-i\sin z\end{aligned}}$

が得えられるから、これを連立れんりつさせて解とくことにより、正弦せいげん関数かんすう・余弦よげん関数かんすうの指数しすう関数かんすうを用もちいた表現ひょうげんが可能かのうとなる。すなわち、

${\begin{aligned}\cos z&={\frac {e^{iz}+e^{-iz}}{2}},\\\sin z&={\frac {e^{iz}-e^{-iz}}{2i}}\end{aligned}}$

が成なり立たつ。この事実じじつにより、級数きゅうすうによらずこの等式とうしきをもって複素数ふくそすうの正弦せいげん・余弦よげん関数かんすうの定義ていぎとすることもある。また、

${\begin{aligned}\cos(iz)&={\frac {e^{-z}+e^{z}}{2}}=\cosh z,\\\sin(iz)&={\frac {e^{-z}-e^{z}}{2i}}=i\sinh z\end{aligned}}$

が成なり立たつ。ここで cosh z, sinh z は双曲線そうきょくせん関数かんすうを表あらわす。この等式とうしきは三角さんかく関数かんすうと双曲線そうきょくせん関数かんすうの関係かんけい式しきと捉とらえることもできる。複素数ふくそすう z を z = x + iy (x, y ∈ R) と表現ひょうげんすると、加法かほう定理ていりより

${\begin{aligned}\cos z&=\cos(x+iy)=\cos x\cosh y-i\sin x\sinh y,\\\sin z&=\sin(x+iy)=\sin x\cosh y+i\cos x\sinh y\end{aligned}}$

が成なり立たつ。

他たの三角さんかく関数かんすうは cscz = 1 / sinz, secz = 1 / cosz, tanz = sinz / cosz, cotz = cosz / sinz によって定義ていぎできる。

• 
  cos(x + iy) の実み部ぶのグラフ
• 
  cos(x + iy) の虚きょ部ぶのグラフ
• 
  sin(x + iy) の実み部ぶのグラフ
• 
  sin(x + iy) の虚きょ部ぶのグラフ

球面きゅうめん三角さんかく法ほう

詳細しょうさいは「球面きゅうめん三角さんかく法ほう」を参照さんしょう

球面きゅうめんの三角形さんかっけい ABC の内角ないかくを a, b, c, 各かく頂点ちょうてんの対辺たいへんに関かんする球たまの中心ちゅうしん角かくを αあるふぁ, βべーた, γがんま とするとき、次つぎのような関係かんけいが成立せいりつする。余弦よげん公式こうしきや正弦せいげん余弦よげん公式こうしきは式しきの対称たいしょう性せいにより各かく記号きごうを入いれ替かえたものも成立せいりつする。

正弦せいげん公式こうしき

sina : sinb : sinc = sinαあるふぁ : sinβべーた : sinγがんま

余弦よげん公式こうしき

cosa = −cosb cosc + sinb sinc cosαあるふぁ

余弦よげん公式こうしき

cosαあるふぁ = cosβべーた cosγがんま + sinβべーた sinγがんま cosa

正弦せいげん余弦よげん公式こうしき

sina cosβべーた = cosb sinc − sinb cosc cosαあるふぁ

語源ごげん　

三角さんかく関数かんすうの英語えいごの名称めいしょうの語源ごげんについて記しるす。

sineはもとはchord-half(半はん弦つる)を意味いみするサンスクリット jya ̄-ardha起源きげんであり、省略形しょうりゃくけいji ̄va ̄がアラビア語ごに音訳おんやくされてjibaとなったが、1145年ねんにチェスターのロバートがフワーリズミーのヒサーブ・アル＝ジャブル・ワル＝ムカーバラをラテン語らてんごに翻訳ほんやくする際さいに、jaibと混同こんどうした事ことで胸むね、湾わんの意味いみのsinusと翻訳ほんやくされた。

tangentは”touching”を意味いみするラテン語らてんごtangens由来ゆらいで、secantは”cutting”を意味いみするラテン語らてんごsecans由来ゆらいである。

cosine、cotangent、cosecantはそれぞれ接頭せっとう辞じのco-がついた形かたちであり、co-はcofunctionと共通きょうつうし、これはcompliment angle(直角ちょっかく三角形さんかっけいの直角ちょっかくでないもう一ひとつの角かく、余よ角かく)に対たいするsine、tangent、secantという意味いみである。cosine、cotangentが初はじめて書かかれた形かたちで確認かくにんされるのは1620年ねんのエドマンド・ガンターによる”Canon triangulorum”の中なかである。ラテン語らてんごのcosinusとして登場とうじょうし、これはsinus complementiの略りゃくである。

日本語にほんごの正弦せいげん、余弦よげんに関かんしては、徐じょ光ひかり啓けいらが編纂へんさんした『崇たかし禎ただし暦れき書しょ』の中なかで、羅ら雅みやび谷たにが1631年ねんに著あらわした『測量そくりょう全ぜん義ぎ』の八はち線せんのうちに見みられる。「正ただし」の漢字かんじには、「真向まむかいの」「主おもとなるもの」という意味いみがある。

「三角さんかく法ほうの歴史れきし」も参照さんしょう

参考さんこう文献ぶんけん

• Maor, Eli (1998). Trigonometric Delights. Princeton University Press. ISBN 978069105754-5 
• 志賀しが浩二こうじ『数かずの大だい航海こうかい―対数たいすうの誕生たんじょうと広ひろがり』日本にっぽん評論ひょうろん社しゃ、1999年ねん7月がつ。ISBN 978-4-535-78289-1。 
• 高瀬たかせ正ただし仁ひとし『古典こてん的てき難問なんもんに学まなぶ微分びぶん積分せきぶん』共立きょうりつ出版しゅっぱん、2013年ねん7月がつ。ISBN 978-4-320-11041-0。 
• Vinogradov, Ivan Matveyevich (2004-09-10). The Method of Trigonometrical Sums in the Theory of Numbers (revised ed.). Dover. ISBN 978-048643878-8 
• 黒川くろかわ信重のぶしげ、小山こやま信也しんや『多重たじゅう三さん角かく関数かんすう論ろん講義こうぎ』日本にっぽん評論ひょうろん社しゃ、2010年ねん11月8日にち。ISBN 978-4-535-785557。 
• 杉浦すぎうら光夫みつお『解析かいせき入門にゅうもんI』東京大学とうきょうだいがく出版しゅっぱん会かい〈基礎きそ数学すうがく2〉、1980年ねん。ISBN 978-4-13-062005-5。 
• 黒田くろだ成俊なりとし『微分びぶん積分せきぶん』共立きょうりつ出版しゅっぱん〈共立きょうりつ講座こうざ21世紀せいきの数学すうがく 第だい1巻かん〉、2002年ねん。ISBN 978-4320015531。 
• 高木たかぎ貞治さだはる『定本ていほん 解析かいせき概論がいろん』（改訂かいてい第だい3版はん）岩波書店いわなみしょてん、2010年ねん。ISBN 978-4000052092。 
• 小平こだいら邦彦くにひこ『解析かいせき入門にゅうもんI』（軽装けいそう版ばん）岩波書店いわなみしょてん、2003年ねん。ISBN 978-4000051927。 

関連かんれん項目こうもく

• 正弦せいげん定理ていり
• 余弦よげん定理ていり
• 正接せいせつ定理ていり
• 球面きゅうめん三角さんかく法ほう
• コサイン4乗じょう則そく
• ベクトルのなす角かく - cos 関数かんすうを用もちいて表現ひょうげんされる。
• ドット積せき
• クロス積せき
• ベッセル関数かんすう
• sinc関数かんすう
• 指数しすう関数かんすう
• 双曲線そうきょくせん関数かんすう
• オイラーの公式こうしき
• 円えん - 正せい円えんの三角さんかく関数かんすうとの関係かんけい
• ベジェ曲線きょくせん - 三角さんかく関数かんすうのベジエ曲線きょくせんによる近似きんじ
• テイラー展開てんかい - コンピュータ上うえでの三角さんかく関数かんすうの実装じっそうに使用しよう
• 算数さんすうチャチャチャ - 歌詞かしに三角さんかく関数かんすうの問題もんだいの解とき方かたが含ふくまれる
• 3次元じげんコンピュータグラフィックス

外部がいぶリンク

• 三角さんかく比ひの近似きんじ値ち表ひょう
• Weisstein, Eric W. "Trigonometric Functions". mathworld.wolfram.com (英語えいご).
• 江戸えど時代じだいの三角さんかく関数かんすう表ひょう(これなあに)
• 『三角さんかく関数かんすう』 - コトバンク