球面 きゅうめん 英語 えいご sphere )是 これ 三 さん 中 ちゅう 完全 かんぜん 的 てき 几何 物体 ぶったい 圆球 的 てき 表面 ひょうめん 二 に 圆 ”包 つつみ 圆盘 ”那 な
就像在 ざい 球面 きゅうめん 在 ざい 数学 すうがく 上 じょう 定 てい 点 てん 的 てき 集合 しゅうごう r [ 1] r 是 ぜ 球 だま 的 てき 半径 はんけい 球 たま 由 よし 定点 ていてん 小 しょう r 的 てき 所有 しょゆう 点 てん 的 てき 体 たい 定点 ていてん 球心 きゅうしん 球 たま 的 てき 半径 はんけい 和 わ 球心 きゅうしん 球面 きゅうめん 的 てき 半径 はんけい 和 わ 中心 ちゅうしん 都 と 在 ざい 球面 きゅうめん 上 じょう 的 てき 最 さい 段通 だんつう 心 しん 度 ど 是 ぜ 半径 はんけい 的 てき 球面 きゅうめん 和 わ 球体 きゅうたい 的 てき 直径 ちょっけい
尽 つき 管 かん 在 ざい 数学 すうがく 之 の 外 そと 球面 きゅうめん 和 かず 球 たま 有 ゆう 使用 しよう 但 ただし 在 ざい 数学 すうがく 中 ちゅう 是 ぜ 明 あかり 区分 くぶん 的 てき 球面 きゅうめん 是 ぜ 欧 おう 得 とく 空 そら 内的 ないてき 二 に 面 めん 球 たま 是 ぜ 一 いち 三 さん 形 がた 包括 ほうかつ 球面 きゅうめん 和 わ 球面 きゅうめん 内部 ないぶ 的 てき 一切 いっさい 闭球 ),不 ふ 常 つね 定 てい 只 ただ 包括 ほうかつ 球面 きゅうめん 内部 ないぶ 的 てき 所有 しょゆう 点 てん 不 ふ 包括 ほうかつ 球面 きゅうめん 上 じょう 的 てき 点 てん 开球 )。这种区 く 不 ふ 保持 ほじ 不 ふ 尤 ゆう 在 ざい 旧 きゅう 的 てき 数学 すうがく 文献 ぶんけん 里 さと 球面 きゅうめん 被 ひ 当 とう 作 さく 固体 こたい 在 ざい 平面 へいめん 上 うえ 混用 こんよう 和 かず 的 てき 情 じょう 似 に
在 ざい 解析 かいせき 中 なか 球心 きゅうしん (x 0 , y 0 , z 0 ) 半径 はんけい r 的 てき 球面 きゅうめん 是 ぜ 下面 かめん 方 かた 程 ほど 的 てき 所有 しょゆう 点 てん (x , y , z ) 的 てき 轨迹
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
+
(
z
−
z
0
)
2
=
r
2
.
{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}.}
令 れい a, b, c, d, e 数 すう a ≠ 0
x
0
=
−
b
a
,
y
0
=
−
c
a
,
z
0
=
−
d
a
,
ρ ろー =
b
2
+
c
2
+
d
2
−
a
e
a
2
.
{\displaystyle x_{0}={\frac {-b}{a}},\quad y_{0}={\frac {-c}{a}},\quad z_{0}={\frac {-d}{a}},\quad \rho ={\frac {b^{2}+c^{2}+d^{2}-ae}{a^{2}}}.}
如果
ρ ろー <
0
{\displaystyle \rho <0}
面 めん 的 てき 方 かた 程 ほど
f
(
x
,
y
,
z
)
=
a
(
x
2
+
y
2
+
z
2
)
+
2
(
b
x
+
c
y
+
d
z
)
+
e
=
0
{\displaystyle f(x,y,z)=a(x^{2}+y^{2}+z^{2})+2(bx+cy+dz)+e=0}
没 ぼつ 有 ゆう 根 ね 称 しょう 虚 きょ 球面 きゅうめん 的 まと 方 かた 程 ほど
ρ ろー =
0
{\displaystyle \rho =0}
f
(
x
,
y
,
z
)
=
0
{\displaystyle f(x,y,z)=0}
的 てき 唯 ただ 一 いち 解 かい 是 ぜ 点 てん
P
0
=
(
x
0
,
y
0
,
z
0
)
{\displaystyle P_{0}=(x_{0},y_{0},z_{0})}
程 ほど 称 たたえ 作 づく 点 てん 球面 きゅうめん 的 まと 方 かた 程 ほど 一 いち 在 ざい
ρ ろー >
0
{\displaystyle \rho >0}
的 てき 情 じょう
f
(
x
,
y
,
z
)
=
0
{\displaystyle f(x,y,z)=0}
是 ぜ 球面 きゅうめん 的 てき 方 かた 程 ほど 中心 ちゅうしん 是 ぜ
P
0
{\displaystyle P_{0}}
半径 はんけい 是 ぜ
ρ ろー
{\displaystyle {\sqrt {\rho }}}
[ 1]
如果上述 じょうじゅつ 等式 とうしき 中 ちゅう 的 てき a 是 ぜ 零 れい 那 な f (x , y , z ) = 0平面 へいめん 方 かた 程 ほど 因 よし 平面 へいめん 可 か 球心 きゅうしん 在 ざい 无穷远点 的 てき 球面 きゅうめん [ 2]
半径 はんけい
r
>
0
{\displaystyle r>0}
中心 ちゅうしん 在 ざい
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
的 てき 球面 きゅうめん 上 じょう 的 てき 点 てん 可 か 成 なり 参 さん 数 すう 方 ぽう 程 ほど
x
=
x
0
+
r
sin
φ ふぁい cos
θ しーた
y
=
y
0
+
r
sin
φ ふぁい sin
θ しーた (
0
≤
φ ふぁい ≤
π ぱい ,
0
≤
θ しーた <
2
π ぱい )
z
=
z
0
+
r
cos
φ ふぁい
{\displaystyle {\begin{aligned}x&=x_{0}+r\sin \varphi \;\cos \theta \\y&=y_{0}+r\sin \varphi \;\sin \theta \qquad (0\leq \varphi \leq \pi ,\;0\leq \theta <2\pi )\\z&=z_{0}+r\cos \varphi \,\end{aligned}}}
[ 3] 以原点 てん 中心 ちゅうしん 的 てき 任意 にんい 半径 はんけい 的 てき 球面 きゅうめん 是 ぜ 以下 いか 微分 びぶん 形式 けいしき 的 てき 曲面 きょくめん
x
d
x
+
y
d
y
+
z
d
z
=
0.
{\displaystyle x\,\mathrm {d} x+y\,\mathrm {d} y+z\,\mathrm {d} z=0.}
这个方 かた 程 ほど 反映 はんえい 了 りょう 在 ざい 球面 きゅうめん 上 じょう 行 ぎょう 点 てん 的 てき 位置 いち (x , y , z ) 和 かず 速度 そくど 向 むこう 量 りょう (dx , dy , dz ) 彼此 ひし 正 せい 的 てき
球面 きゅうめん 任 にん 何 なに 直径 ちょっけい 把 わ 一周 いっしゅう 形成 けいせい 的 てき 表面 ひょうめん 来 らい 由 よし 是 ぜ 一 いち 殊 こと 的 てき 椭圆 ,所以 ゆえん 球面 きゅうめん 形成 けいせい 的 てき 曲面 きょくめん 长球面 めん ;如果绕短轴旋转,就会形成 けいせい 一 いち 球面 きゅうめん [ 4]
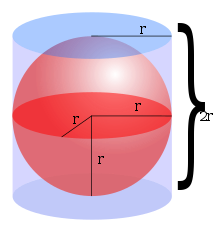
将 はた 外接 がいせつ 到 いた 一 いち 面 めん 上 じょう 在 ざい 三 さん 球面 きゅうめん 内包 ないほう 体 からだ 即 そく 球 たま 的 てき 体 からだ 是 これ
V
=
4
3
π ぱい
r
3
{\displaystyle V={\frac {4}{3}}\pi r^{3}}
其中 r 是 ぜ 球面 きゅうめん 的 てき 半径 はんけい 阿 おもね 基 もと 米 まい 德 とく 首 くび 先 さき 出 で 了 りょう 公式 こうしき 他 た 通 どおり 明 あかり 球体 きゅうたい 内的 ないてき 体 たい 球体 きゅうたい 内部 ないぶ 与 あずか 外接 がいせつ 圆柱体 たい (具有 ぐゆう 与 あずか 球体 きゅうたい 直径 ちょっけい 相等 そうとう 的 てき 高度 こうど 和 わ 直径 ちょっけい 内部 ないぶ 之 の 体 たい 出 で 式 しき [ 5] 可 か 据 すえ 祖 そ 原理 げんり 得 え 到 いた 式 しき 使用 しよう 得 とく 出 で 即 そく 用 よう 定 てい 的 てき 厚 あつ 度 たび 小 しょう 的 てき x x = −r 到 いた x = r 堆 うずたか 来 らい 的 てき 体 からだ 和 わ 假 かり 球面 きゅうめん 半径 はんけい r 点 てん 心 しん
在任 ざいにん 何 なん 的 てき x 体 たい 增量 ぞうりょう Δ でるた 近似 きんじ 等 とう x 面 めん 度 ど Δ でるた 的 てき 乘 じょう
Δ でるた V
≈
π ぱい
y
2
⋅
Δ でるた x
.
{\displaystyle \Delta V\approx \pi y^{2}\cdot \Delta x.}
当 とう 最 さい 厚 あつし 的 てき 那 な 所有 しょゆう 增量 ぞうりょう 的 てき
V
=
lim
|
|
T
|
|
→
0
∑
π ぱい
y
2
⋅
Δ でるた x
.
{\displaystyle V=\lim _{||T||\to 0}\sum \pi y^{2}\cdot \Delta x.}
其中 ||T 表示 ひょうじ 当 とう 取分 とりぶん 割 わり T 最 さい 厚 あつし 的 てき 那 な 厚 あつ 度 たび 体 たい
V
=
∫
−
r
r
π ぱい
y
2
d
x
.
{\displaystyle V=\int _{-r}^{r}\pi y^{2}\mathrm {d} x.}
在任 ざいにん 何 なん 的 てき x x y r 都 と 可 か 成 なり 一 いち 角 かく 三角形 さんかっけい 因 いん 勾股定理 ていり 得 とく 出 で
y
2
=
r
2
−
x
2
.
{\displaystyle y^{2}=r^{2}-x^{2}.}
将 はた 上 うえ 式 しき 代入 だいにゅう 得 え 到 いた
V
=
∫
−
r
r
π ぱい (
r
2
−
x
2
)
d
x
,
{\displaystyle V=\int _{-r}^{r}\pi (r^{2}-x^{2})\mathrm {d} x,}
积分之 の 后 きさき 出 で
V
=
π ぱい
[
r
2
x
−
x
3
3
]
−
r
r
=
π ぱい
(
r
3
−
r
3
3
)
−
π ぱい
(
−
r
3
+
r
3
3
)
=
4
3
π ぱい
r
3
.
{\displaystyle V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\right)={\frac {4}{3}}\pi r^{3}.}
另外,此公式 しき 球 だま 坐 すわ 体 たい 可 か 成 なり
d
V
=
ρ ろー
2
sin
φ ふぁい
d
ρ ろー
d
θ しーた
d
φ ふぁい
{\displaystyle \mathrm {d} V=\rho ^{2}\sin \varphi \,\mathrm {d} \rho \,\mathrm {d} \theta \,\mathrm {d} \varphi }
因 いん 到 いた 三重 みえ 算出 さんしゅつ
V
=
∫
0
2
π ぱい
d
θ しーた
∫
0
π ぱい
d
φ ふぁい
∫
0
r
ρ ろー
2
sin
θ しーた
d
ρ ろー =
4
3
π ぱい
r
3
.
{\displaystyle V=\int _{0}^{2\pi }\mathrm {d} \theta \,\int _{0}^{\pi }\mathrm {d} \varphi \,\int _{0}^{r}\rho ^{2}\sin \theta \mathrm {d} \rho ={\frac {4}{3}}\pi r^{3}.}
对于大 だい 多数 たすう 用途 ようと 立方体 りっぽうたい 的 てき 内接 ないせつ 球 だま 的 てき 体 からだ 近似 きんじ 立方体 りっぽうたい 体 たい 因 いん V = π ぱい / 6 d 3 d 是 ぜ 球面 きゅうめん 的 てき 直径 ちょっけい 立方体 りっぽうたい 的 てき π ぱい / 6 例 れい 直径 ちょっけい 的 てき 球 たま 的 てき 体 からだ 的 てき 立方体 りっぽうたい 体 たい 或 ある 3 。
半径 はんけい r 的 てき 球体 きゅうたい 的 てき 表面積 ひょうめんせき
A
=
4
π ぱい
r
2
.
{\displaystyle A=4\pi r^{2}.}
阿 おもね 基 もと 米 まい 德 とく 首 くび 先 さき 根 ね 据 すえ 外接 がいせつ 体 たい 的 てき 投影 とうえい 是 ぜ 保持 ほじ 面 めん 事 ごと 公式 こうしき [ 6] [ 7] 即 そく 球 だま 的 てき 表面 ひょうめん 体 たい 式 しき r 的 てき 导数 ,因 いん 半径 はんけい r 的 てき 球体 きゅうたい 的 てき 体 からだ 半径 はんけい 到 いた 半径 はんけい r 嵌 はま 在 ざい 小 しょう 的 てき 厚 あつ 度 ど 下 か 任 にん 何 なん 球 だま 内外 ないがい 表面 ひょうめん 面 めん 相等 そうとう 的 てき 半径 はんけい r 体 たい 可 か 是 ぜ 半径 はんけい r 表面 ひょうめん 小 しょう 厚 あつ 度 ど 的 てき 乘 じょう
在任 ざいにん 何 なん 半径 はんけい r [ 8] 体 からだ 增量 ぞうりょう Δ でるた 等 とう 半径 はんけい r 面 めん A (r )与 あずか 球 たま 度 ど Δ でるた 的 てき 乘 じょう
Δ でるた V
≈
A
(
r
)
⋅
Δ でるた r
.
{\displaystyle \Delta V\approx A(r)\cdot \Delta r.}
总体积是所有 しょゆう 球 だま
V
≈
∑
A
(
r
)
⋅
Δ でるた r
.
{\displaystyle V\approx \sum A(r)\cdot \Delta r.}
该等式 しき 在 ざい 最 さい 厚 あつし 的 てき 那 な 一 いち Δ でるた [ 9]
V
=
∫
0
r
A
(
r
)
d
r
.
{\displaystyle V=\int _{0}^{r}A(r)\,\mathrm {d} r.}
代入 だいにゅう V
4
3
π ぱい
r
3
=
∫
0
r
A
(
r
)
d
r
.
{\displaystyle {\frac {4}{3}}\pi r^{3}=\int _{0}^{r}A(r)\,\mathrm {d} r.}
将 はた 等式 とうしき r 求 もとめ 会得 えとく 到 いた A r 的 てき 函数 かんすう
4
π ぱい
r
2
=
A
(
r
)
.
{\displaystyle 4\pi r^{2}=A(r).}
这通常 つうじょう 写 うつし
A
=
4
π ぱい
r
2
,
{\displaystyle A=4\pi r^{2},}
其中 r 是 ぜ 球面 きゅうめん 的 てき 半径 はんけい
再来 さいらい 看 み 一 いち 法 ほう 球面 きゅうめん 上 じょう 的 てき 面 めん 可 か 球 だま 坐 すわ dA = r 2 sin φ ふぁい θ しーた φ ふぁい 用 よう 笛 ふえ 表示 ひょうじ 的 てき 面 めん 写 うつし 成 なり
d
S
=
r
r
2
−
∑
i
≠
k
x
i
2
∏
i
≠
k
d
x
i
,
∀
k
.
{\displaystyle \mathrm {d} S={\frac {r}{\sqrt {r^{2}-{\displaystyle \sum _{i\neq k}x_{i}^{2}}}}}\prod _{i\neq k}\mathrm {d} x_{i},\;\forall k.}
更 さら 一般 いっぱん 性的 せいてき 表 ひょう 面 めん 条目 じょうもく
因 いん 面 めん 积分 得 え 到 いた
A
=
∫
0
2
π ぱい
d
θ しーた
∫
0
π ぱい
r
2
sin
φ ふぁい
d
φ ふぁい =
∫
0
2
π ぱい
[
−
r
2
cos
φ ふぁい
]
0
π ぱい
d
θ しーた =
4
π ぱい
r
2
.
{\displaystyle A=\int _{0}^{2\pi }\mathrm {d} \theta \,\int _{0}^{\pi }r^{2}\sin {\varphi }\mathrm {d} \varphi =\int _{0}^{2\pi }[-r^{2}\cos {\varphi }]_{0}^{\pi }\,\mathrm {d} \theta =4\pi r^{2}.}
上 うえ 的 てき 球体 きゅうたい 被 ひ 是 ぜ 最 さい 精 せい 人造 じんぞう 球体 きゅうたい 之 の 一 いち 折 おり 射 しゃ 出 で 背景 はいけい 中 ちゅう 爱因斯坦 的 てき 画像 がぞう 球体 きゅうたい 是 ぜ 引力 いんりょく 探 さがせ 中 ちゅう 所用 しょよう 的 てき 熔融 ようゆう 石英 せきえい 陀螺仪 ,它在形状 けいじょう 上 じょう 和 かず 完 かん 美 び 球体 きゅうたい 之 の 不 ふ 超 ちょう 子 こ 不 ふ 到 いた 纳米 )厚 あつ 度 たび 年 ねん 月 がつ 日 にち 一 いち 自 じ 澳大利 おおとし 的 てき 科学 かがく 家 か 宣 せん 称 たたえ 他 た 造 づくり 出 で 了 りょう 更 さら 加 か 接近 せっきん 完 かん 美的 びてき 球体 きゅうたい 准 じゅん 背景 はいけい 是 ぜ 当年 とうねん 科学 かがく 家 か 一 いち 千 せん 克 かつ 的 てき 新 しん [ 10] 球面 きゅうめん 是 ぜ 包 つつみ 定 てい 体 からだ 所有 しょゆう 曲面 きょくめん 中 ちゅう 面 めん 最小 さいしょう 的 てき 球面 きゅうめん 表面 ひょうめん 所有 しょゆう 曲面 きょくめん 中 ちゅう 包 つつみ 最大 さいだい 的 てき 因 よし 面 めん 在 ざい 自然 しぜん 界 かい 中出 なかいで 例 れい 和 わ 小 しょう 水滴 すいてき 大 だい 球形 きゅうけい 因 いん 表面 ひょうめん 会 かい 局部 きょくぶ 最小 さいしょう 化 か 表面 ひょうめん
球 たま 的 てき 与 あずか 表面 ひょうめん 比 ひ 称 しょう 表面 ひょうめん 可 か 上述 じょうじゅつ 等式 とうしき 表示 ひょうじ 出来 でき
S
S
A
=
A
V
ρ ろー
=
3
r
ρ ろー
,
{\displaystyle \mathrm {SSA} ={\frac {A}{V\rho }}={\frac {3}{r\rho }},}
其中 ρ ろー 密度 みつど 与 あずか 体 からだ 比 ひ
球面 きゅうめん 由 よし 更 さら 一般 いっぱん 地 ち 球面 きゅうめん 由 よし 例 れい 与一 よいち 面相 めんそう 切 きり 等 とう 等 とう [ 11] 似 に
因 いん
通 つう 面 めん 方 かた 程 ほど 的 てき 共同 きょうどう 解 かい 可 か 出 で 球 だま 相 しょう 一 いち 包含 ほうがん 的 てき 平面 へいめん 称 しょう 作 さく 相 しょう 的 てき 基本 きほん 平面 へいめん [ 12] 基本 きほん 平面 へいめん 是 ぜ 一 いち 平面 へいめん 但 ただし 可能 かのう 是 ぜ 虚 きょ 球面 きゅうめん 没 ぼつ 有 ゆう 公共 こうきょう 点 てん 可能 かのう 由 よし 点 てん 球面 きゅうめん 在 ざい 相 しょう 切 きり [ 13]
在 ざい 点 てん 球面 きゅうめん 之 の 是 ぜ 由 よし 球体 きゅうたい 的 てき 切 きり 面 めん 的 てき 二 に 面 めん 角 かく 球面 きゅうめん 在 ざい 相 しょう 的 てき 所有 しょゆう 点 てん 都 と 是 ぜ 相 しょう 同 どう 的 てき [ 14] 当 とう 当 とう 的 てき 球心 きゅうしん 之 の 的 てき 平方 へいほう 等 とう 半径 はんけい 的 てき 平方和 へいほうわ 的 てき 才 ざい 是 ぜ 直角 ちょっかく 相互 そうご 正 せい [ 2]
如果 f (x , y , z ) = 0和 わ g (x , y , z ) = 0是 ぜ 不同 ふどう 球面 きゅうめん 的 てき 方 かた 程 ほど 那 な
s
f
(
x
,
y
,
z
)
+
t
g
(
x
,
y
,
z
)
=
0
{\displaystyle sf(x,y,z)+tg(x,y,z)=0}
当 とう 参 さん 数 すう s 和 わ t 是 ぜ 任意 にんい 球面 きゅうめん 方 かた 程 ほど 式 しき 的 てき 所有 しょゆう 球体 きゅうたい 的 てき 集合 しゅうごう 称 しょう 原始 げんし 球体 きゅうたい 的 てき 球面 きゅうめん 束 たば 在 ざい 定 てい 允 まこと 面 めん 是 ぜ 一 いち 面 めん 半径 はんけい 球心 きゅうしん 在 ざい 果 はて 原始 げんし 球面 きゅうめん 都 と 是 ぜ 平面 へいめん 那 な 的 てき 所有 しょゆう 球面 きゅうめん 都 と 是 ぜ 平面 へいめん 否 いや 球面 きゅうめん 束 たば 中 ちゅう 只 ただ 会 かい 有 ゆう 一 いち 面 めん 基本 きほん 平面 へいめん [ 2]
如果球面 きゅうめん 束 たばね 不 ふ 是 ぜ 由 よし 所有 しょゆう 平面 へいめん 那 な 三 さん 型 がた 的 てき 束 たば [ 13]
若 わか 球面 きゅうめん 相 しょう 一 いち C 面 めん 束 たば 由 よし 包含 ほうがん C 的 てき 所有 しょゆう 球面 きゅうめん 包括 ほうかつ 基本 きほん 平面 へいめん 球面 きゅうめん 束 たば 中 ちゅう 所有 しょゆう 普通 ふつう 球面 きゅうめん 的 てき 中心 ちゅうしん 位 い C 的中 てきちゅう 心 こころ 直 ちょく 基本 きほん 平面 へいめん 的 てき 直 ちょく 下面 かめん 称 しょう 作 さく 中心 ちゅうしん 上 じょう 若 わか 球面 きゅうめん 相 しょう 一 いち 球面 きゅうめん 束 たば 的 てき 所有 しょゆう 球面 きゅうめん 通 どおり 但 ただし 是 ぜ 普通 ふつう 球面 きゅうめん 不 ふ 相 あい 没 ぼつ 有 ゆう 真正 しんせい 的 てき 公共 こうきょう 点 てん 中心 ちゅうしん 直 ちょく 基本 きほん 平面 へいめん 一 いち 平面 へいめん 但 ただし 包含 ほうがん 了 りょう 一 いち 假想 かそう 的 てき 如果球面 きゅうめん 相 しょう 一 いち 点 てん A 所有 しょゆう 在 ざい 面 めん 内的 ないてき 球面 きゅうめん A 都 みやこ 是 ただし 相 しょう 切 きり 的 てき 同 どう 基本 きほん 面 めん 是 ぜ 所有 しょゆう 面 めん 的 てき 公 おおやけ 切 きり 面 めん 中心 ちゅうしん A 直 ちょく 基本 きほん 平面 へいめん 所有 しょゆう 基本 きほん 平面 へいめん 的 てき 固定 こてい 点 てん 到 いた 球面 きゅうめん 束 たば 的 てき [ 13]
基本 きほん 平面 へいめん 是 ぜ 与 あずか 球面 きゅうめん 束 たば 中 ちゅう 所有 しょゆう 球面 きゅうめん 正 せい 所有 しょゆう 球面 きゅうめん 的 てき 中心 ちゅうしん 的 てき 与 あずか 球体 きゅうたい 束 たば 的 てき 任 にん 何 なん 球体 きゅうたい 正 せい 球体 きゅうたい 与 あずか 球面 きゅうめん 束 たば 的 てき 所有 しょゆう 球面 きゅうめん 正 せい 中心 ちゅうしん 位 い 面 めん 束 たば 的 てき 基本 きほん 平面 へいめん 中 ちゅう [ 13]
穿 ほじ 心的 しんてき 的 てき 交点 こうてん 称 しょう 径 みち 点 てん 大 だい 是 ぜ 球面 きゅうめん 上 じょう 的 てき 一 いち 与 あずか 球面 きゅうめん 具有 ぐゆう 相 しょう 同 どう 的中 てきちゅう 心 こころ 和 かず 半径 はんけい 大 だい 所在 しょざい 的 てき 平面 へいめん 能 のう 将 はた 球面 きゅうめん 分 ぶん 成 なり 相 しょう 同 どう 的 てき 部分 ぶぶん 球面 きゅうめん 的 てき 称 しょう 圆面截口 (spheric sections)。圆面截口均 ひとし 除 じょ 了 りょう 大 だい 外的 がいてき 小 しょう [ 15]
球面 きゅうめん 上 じょう 不同 ふどう 非 ひ 点 てん 之 の 最短 さいたん 是 ぜ 点 てん 的 てき 唯 ただ 有 ゆう 了 りょう 大 だい 大 だい 成 なり 黎 はじむ
若 わか 将 はた 球面 きゅうめん 上 じょう 任意 にんい 北 きた 与 あずか 相 しょう 的 てき 点 てん 称 しょう 南 みなみ 赤道 あかみち 与 あずか 点 てん 等 とう 大 だい 的 てき 大 だい 称 しょう 子 こ 午 うま 或 ある 经线 ,过这两个极点的 てき 直 ちょく 称 しょう 纬度 则是球面 きゅうめん 上 じょう 与 あずか 赤道 せきどう 平行 へいこう 的 てき 用 よう 地球 ちきゅう 表面 ひょうめん 一 いち 近似 きんじ 球面 きゅうめん 的 てき 天体 てんたい 大地 だいち 水 すい 准 じゅん 面 めん
任 にん 何 なん 心的 しんてき 平面 ひらおもて 都 と 把 わ 成 なり 相等 そうとう 的 てき 半球 はんきゅう 面 めん 心 しん 的 てき 任 にん 何 なん 相 しょう 平面 ひらおもて 都 と 将 はた 球体 きゅうたい 面 めん 二 に 角形 かくがた 点 てん 全部 ぜんぶ 与 あずか 位 くらい 面 めん 上 じょう 的 てき 点 てん 重合 じゅうごう
球体 きゅうたい 的 てき 商 しょう 空 そら 实射影 しゃえい 平面 へいめん ,它也可 か 看 み 作 さく 是 ぜ 北半球 きたはんきゅう 赤道 せきどう 的 てき 点 てん 被 ひ
有 ゆう 半球 はんきゅう 是 ぜ 黎 はじむ 的 てき 最 さい 佳 けい 最小 さいしょう 面 めん 等 とう 充 たかし
球面 きゅうめん 可 か 任意 にんい 的 てき 空 そら 任意 にんい 自然 しぜん 数 すう n n 球面 きゅうめん 常 つね 写 うつし S n 是 ぜ n + 1得 とく 空 そら 空 そら r 的 まと 点 てん 的 てき 集合 しゅうごう r 与 あずか 前面 ぜんめん 一 いち 是正 ぜせい 特 とく
S 0 球体 きゅうたい 是 ぜ 的 てき 区 く [−r , r ] 的 てき 一 いち 点 てん S 1 球面 きゅうめん 是 ぜ 半径 はんけい r 的 てき 圆 S 2 球面 きゅうめん 是 ぜ 普通 ふつう 的 てき 球面 きゅうめん S 3 3-球面 きゅうめん 是 ぜ n > 2的 てき 球面 きゅうめん 有 ゆう 作 さく 超 ちょう 球面 きゅうめん
以原点 てん 中心 ちゅうしん 的 てき 半径 はんけい n 球面 きゅうめん 表示 ひょうじ S n 通常 つうじょう 称 しょう n 球面 きゅうめん 注意 ちゅうい 普通 ふつう 球面 きゅうめん 是 ぜ 一 いち 球面 きゅうめん 因 いん 是 ぜ 一 いち 二 に 面 めん 嵌入 かんにゅう 在 ざい 三 さん
单位(n -1球面 きゅうめん 的 てき 表面 ひょうめん
2
π ぱい
n
2
Γ がんま
(
n
2
)
{\displaystyle {\frac {2\pi ^{\frac {n}{2}}}{\Gamma \left({\frac {n}{2}}\right)}}}
其中Γ がんま z )是 ぜ 欧 おう 拉 ひしげ 发现的 てき 伽 とぎ 数 すう 。
表面 ひょうめん
{
(
2
π ぱい
)
n
/
2
r
n
−
1
2
⋅
4
⋯
(
n
−
2
)
,
if
n
is even
;
2
(
2
π ぱい
)
(
n
−
1
)
/
2
r
n
−
1
1
⋅
3
⋯
(
n
−
2
)
,
if
n
is odd
.
{\displaystyle {\begin{cases}\displaystyle {\frac {(2\pi )^{n/2}\,r^{n-1}}{2\cdot 4\cdots (n-2)}},&{\text{if }}n{\text{ is even}};\\\\\displaystyle {\frac {2(2\pi )^{(n-1)/2}\,r^{n-1}}{1\cdot 3\cdots (n-2)}},&{\text{if }}n{\text{ is odd}}.\end{cases}}}
体 からだ 面 めん r / n 或 ある 者 もの
{
(
2
π ぱい
)
n
/
2
r
n
2
⋅
4
⋯
n
,
if
n
is even
;
2
(
2
π ぱい
)
(
n
−
1
)
/
2
r
n
1
⋅
3
⋯
n
,
if
n
is odd
.
{\displaystyle {\begin{cases}\displaystyle {\frac {(2\pi )^{n/2}\,r^{n}}{2\cdot 4\cdots n}},&{\text{if }}n{\text{ is even}};\\\\\displaystyle {\frac {2(2\pi )^{(n-1)/2}\,r^{n}}{1\cdot 3\cdots n}},&{\text{if }}n{\text{ is odd}}.\end{cases}}}
对于n 球 たま 的 てき 体 からだ 存在 そんざい 一般 いっぱん 公式 こうしき
更 さら 一般 いっぱん 地 ち 在 ざい 度量 どりょう 空 そら (E ,d ) 中 なか 中心 ちゅうしん x 半径 はんけい r > 0的 てき 球面 きゅうめん 是 ぜ 使 し 得 とく d (x ,y ) = r 的 まと 点 てん y 的 てき 集合 しゅうごう
如果球心 きゅうしん 是 ぜ 位 い E 的 てき 原点 げんてん 赋范 空 そら 那 な 的 てき 定 てい 符号 ふごう 中 ちゅう 没 ぼつ 有 ゆう 提 ひさげ 等 とう 半径 はんけい 例 れい 单位球体 きゅうたい 的 てき 情 じょう
与 あずか 球体 きゅうたい 不同 ふどう 的 てき 是 ぜ 即 そく 使 つかい 是 ぜ 例 れい 在 ざい 欧 おう 德 とく 度量 どりょう Z n 中 なか 只 ただ 有 ゆう r 2 可 か 成 なり 整数 せいすう 的 てき n 平方和 へいほうわ 半径 はんけい r 的 てき 球面 きゅうめん 才 ざい 是非 ぜひ 空 そら 的 てき
在 ざい 拓 つぶせ 中 なか n 球面 きゅうめん 定 てい 与 あずか (n + 1) 球体 きゅうたい 的 てき 同 どう 胚 はい 的 てき 空 そら 因 いん 欧 おう 德 とく n 球体 きゅうたい 同 どう 胚 はい 但 ただし 可能 かのう 缺 かけ 少 しょう 度量 どりょう
0-球面 きゅうめん 是 ぜ
1-球面 きゅうめん 是 ぜ 一 いち 同 どう 胚 はい 意 い 因 よし 例 れい 任 にん 何 なん 的 てき 像 ぞう 是 ぜ 球面 きゅうめん
2-球面 きゅうめん 普通 ふつう 的 てき 球面 きゅうめん 同 どう 胚 はい 意 い 因 よし 例 れい 任 にん 何 なに 类球面 めん 都 と 是 ぜ 球面 きゅうめん n 球面 きゅうめん Sn 没 ぼつ 有 ゆう 边界 的 てき 紧致 拓 つぶせ 形 がた 的 てき 一 いち 子 こ 球面 きゅうめん 不 ふ 光 こう 滑 すべり 的 てき 光 こう 滑 すべり 的 てき 不 ふ 需要 じゅよう 与 あずか 欧 おう 得 とく 球面 きゅうめん 微分 びぶん 同 どう 胚 はい
海 うみ 博 はく 雷 かみなり 定理 ていり 表明 ひょうめい 欧 おう 德 とく n 球面 きゅうめん 是 ぜ 的 てき 球面 きゅうめん 是 ぜ 函数 かんすう ||x 下 しも 集 しゅう 的 てき 逆 ぎゃく 象 ぞう 因 よし 球面 きゅうめん 是 ぜ 的 てき Sn 有界 ゆうかい 的 てき 所以 ゆえん 的 てき
值得注意 ちゅうい 的 てき 是 ぜ 在 ざい 三 さん 中 ちゅう 是 ぜ 可 か 普通 ふつう 的 てき 球面 きゅうめん 内外 ないがい 翻 こぼし 来 らい 的 てき 称 しょう 作 さく 球面 きゅうめん 外 がい 翻 こぼし 中 ちゅう 可能 かのう 会 かい 自 じ 但 ただし 不 ふ 会 かい 任 にん 何 なん 折 おり 痕 こん
球面 きゅうめん 上 じょう 的 てき 大 だい 欧 おう 得 とく 平面 へいめん 的 てき 基本 きほん 要素 ようそ 是 ぜ 点 てん 和 かず 在 ざい 球面 きゅうめん 上 じょう 点 てん 通常 つうじょう 的 てき 意 い 定 てい 的 てき 物 ぶつ 是 ぜ 测地线 ,测地线是一 いち 大圈 たいけん 大 だい 界 かい 定性 ていせい 特 とく 征 せい 是 ぜ 含有 がんゆう 所有 しょゆう 点 てん 的 てき 平面 へいめん 心 しん 弧 こ 表明 ひょうめい 球面 きゅうめん 上 じょう 之 の 最短 さいたん 路 ろ 径 みち 是 ぜ 的 てき 大 だい 的 てき 的 てき 那 な 一 いち 段 だん
经典几何的 てき 定理 ていり 用 よう 面 めん 但 ただし 所有 しょゆう 的 てき 定理 ていり 都 と 是 ぜ 因 いん 面 めん 不能 ふのう 包括 ほうかつ 平行 へいこう 假 かり 在 ざい 球面 きゅうめん 三角 さんかく 学 がく 中 なか 角 かく 是 ぜ 在 ざい 大 だい 球面 きゅうめん 三角 みすみ 学 まなぶ 不同 ふどう 例 れい 球形 きゅうけい 度 ど 任 にん 何 なん 相似 そうじ 的 てき 球面 きゅうめん
球面 きゅうめん 的 てき 一 いち 向 むこう 量 りょう 交叉 こうさ 曲 きょく 曲 きょく 率 りつ 是 ぜ 曲 きょく 率 りつ 球面 きゅうめん 通 つう 定点 ていてん 的 てき 每 まい 将 はた 是 ぜ 半径 はんけい 的 てき 半径 はんけい 意味 いみ 着 ぎ 球面 きゅうめん 上 じょう 的 てき 每 まい 都 と 是 ぜ 在 ざい David Hilbert 和 かず 的 てき 著作 ちょさく 与 あずか 想 そう 象 ぞう [ 16] 一 いち 性 せい 否 ひ 存在 そんざい 定 てい 球面 きゅうめん 之 の 中 なか 因 いん 面 めん 可 か 作 さく 半径 はんけい 大 だい 的 てき 球面 きゅうめん 性 せい
球面 きゅうめん 上 じょう 任意 にんい 点 てん 与 あずか 球心 きゅうしん 的 てき 都 と 是 ぜ 相 しょう 同 どう 的 てき 同 どう 某 ぼう 固定 こてい 点 てん 之 の 之 の 比 ひ 是 ぜ 恒 つね 定 じょう 的 てき 第 だい 可 か 一 いち 球面 きゅうめん 阿波 あわ 容易 ようい 被 ひ 出 で 第 だい 球面 きゅうめん 的 てき 外 そと 和 わ 用 よう 平面 へいめん 的 てき 都 と 是 ぜ 该性质是球面 きゅうめん 独 どく 有 ゆう 的 てき 性 せい 球面 きゅうめん 的 てき 径 みち 周 しゅう 保持 ほじ 不 ふ 曲面 きょくめん 的 てき 径 みち 指 ゆび 面相 めんそう 切 きり 的 てき 平行 へいこう 的 てき 平面 へいめん 的 てき 除 じょ 了 りょう 球面 きゅうめん 之 の 外 そと 的 てき 凸面 とつめん 的 てき 径 みち 是 ぜ 恒 つね 定 てい 不 ふ 例 れい 面 めん 的 てき 周 しゅう 是 ぜ 在 ざい 平面 へいめん 上 じょう 的 てき 正 せい 投影 とうえい 的 てき 中 ちゅう 任意 にんい 性 せい 可 か 出 で 球面 きゅうめん 的 てき 所有 しょゆう 点 てん 都 と 是 ぜ 因 いん 面 めん 上 じょう 的 てき 法 ほう 由 よし 球心 きゅうしん 向 こう 外 そと 的 てき 所以 ゆえん 在 ざい 球面 きゅうめん 上 じょう 任意 にんい 一 いち 点 てん 的 てき 法 ほう 表面 ひょうめん 的 てき 都 と 成 なる 直角 ちょっかく 平面 へいめん 与 あずか 曲面 きょくめん 的 てき 形成 けいせい 的 てき 曲 きょく 法 ほう 曲 きょく 法 ほう 曲 きょく 曲 きょく 率 りつ 被 ひ 称 しょう 法 ほう 曲 きょく 率 りつ 大 だい 多数 たすう 曲面 きょくめん 上大 かみおお 部分 ぶぶん 的 てき 点 てん 不同 ふどう 的 てき 法 ほう 曲 きょく 法 ほう 曲 きょく 率 りつ 同 どう 曲 きょく 率 りつ 的 てき 最大 さいだい 最小 さいしょう 称 しょう 主 しゅ 曲 きょく 率 りつ 任 にん 何 なん 的 てき 曲面 きょくめん 上 じょう 至 いたり 少 しょう 有 ゆう 四 よん 脐点 。脐点上 じょう 所有 しょゆう 的 てき 法 ほう 曲 きょく 率 りつ 是 ぜ 相等 そうとう 的 てき 包括 ほうかつ 主 しゅ 曲 きょく 率 りつ 相等 そうとう 的 てき 可 か 是 ぜ 曲面 きょくめん 上 じょう 最 さい 像 ぞう 球面 きゅうめん 的 てき 点 てん 球面 きゅうめん 上 じょう 所有 しょゆう 法 ほう 曲 きょく 曲 きょく 率 りつ 都 と 是 ぜ 相等 そうとう 的 てき 所以 ゆえん 每 ごと 都 と 是 ぜ 曲面 きょくめん 中 ちゅう 只 ただ 有 ゆう 球面 きゅうめん 和平 わへい 面 めん 具有 ぐゆう 球体 きゅうたい 是 ぜ 没 ぼつ 有 ゆう 中心 ちゅうしん 表面 ひょうめん 的 てき 对于一个给定的法曲线,存在 そんざい 位 い 法 ほう 例 れい 大和 やまと 最小 さいしょう 曲 きょく 率 りつ 的 てき 被 ひ 称 しょう 焦点 しょうてん 所有 しょゆう 的 てき 集合 しゅうごう 形成 けいせい 的 てき 面 めん 叫 さけべ 面 めん
对于大 だい 多数 たすう 曲面 きょくめん 来 らい 焦 こげ 面会 めんかい 形成 けいせい 曲面 きょくめん 在 ざい 对于管 かん 道 どう 曲面 きょくめん
对于圆锥体 たい ,圆柱体 たい 环面 和 かず 曲 きょく 面 めん 都 と 形成 けいせい 曲面 きょくめん
在 ざい 球面 きゅうめん 上 じょう 每 まい 面 めん 形成 けいせい 球面 きゅうめん 上 じょう 的 てき 所有 しょゆう 是 ぜ 曲 きょく 测地线是球面 きゅうめん 表面 ひょうめん 上 じょう 的 てき 曲 きょく 之 の 最短 さいたん 是 ぜ 平面 へいめん 中 ちゅう 直 ちょく 概念的 がいねんてき 球面 きゅうめん 来 らい 一 いち 的 てき 的 てき 曲面 きょくめん 都 と 有 ゆう 性 せい 在 ざい 体 からだ 小 しょう 一定 いってい 的 てき 情 じょう 球面 きゅうめん 的 てき 表面 ひょうめん 最小 さいしょう 表面 ひょうめん 大小 だいしょう 固定 こてい 的 てき 情 じょう 球面 きゅうめん 包 つつみ 最大 さいだい 的 てき 体 からだ 这个性 せい 自 じ 自 じ 等 ひとし 周 しゅう 不等式 ふとうしき 性 せい 例 れい 肥 こえ 中 なか 肥 こえ 包 つつみ 体 たい 表面 ひょうめん 使 つかい 得 とく 面 めん 小 しょう 尽 つき 管 かん 由 よし 重力 じゅうりょく 的 てき 外力 がいりょく 会 かい 使 し 得 とく 肥 こえ 的 てき 形状 けいじょう 在 ざい 所有 しょゆう 已 やめ 定 てい 表面 ひょうめん 凸 とつ 固体 こたい 中 ちゅう 球面 きゅうめん 的 てき 平均 へいきん 曲 きょく 率 りつ 是 ぜ 最小 さいしょう 的 てき 平均 へいきん 曲 きょく 率 りつ 是 ぜ 主 ぬし 曲 きょく 率 りつ 的 てき 平均 へいきん 恒 つね 定 じょう 的 てき 一 いち 因 いん 面 めん 上 じょう 的 てき 所有 しょゆう 点 てん 的 てき 主 あるじ 曲 きょく 率 りつ 都 と 是 ぜ 相等 そうとう 的 てき 球面 きゅうめん 的 てき 平均 へいきん 曲 きょく 率 りつ 是 ぜ 恒 つね 定 じょう 的 てき 球面 きゅうめん 是 ぜ 唯 ただ 小曲 しょうきょく 面 めん 的 てき 面 めん 的 てき 平均 へいきん 曲 きょく 率 りつ 恒 つね 定 じょう 的 てき 球面 きゅうめん 的 てき 高 だか 率 りつ 是 ぜ 一 いち 数 すう 高 こう 率 りつ 是 ぜ 主 ぬし 曲 きょく 率 りつ 的 てき 乘 じょう 与 あずか 曲面 きょくめん 如何 いか 嵌入 かんにゅう 空 そら 因 よし 折 おり 面 めん 会 かい 改 あらため 率 りつ 他 た 高 だか 率 りつ 不 ふ 曲面 きょくめん 球面 きゅうめん 上切 かみぎり 割 わり 所有 しょゆう 的 てき 曲面 きょくめん 都 と 有 ゆう 球面 きゅうめん 是 ぜ 唯 ただ 因 いん 的 てき 高 だか 率 りつ 是 ぜ 一 いち 数 すう 伪球面 めん 是 ぜ 球面 きゅうめん 是 ぜ 由 よし 围绕任 にん 何 なん 在 ざい 原点 げんてん 球 だま 会 かい 将 はた 球面 きゅうめん 映 うつ 射 い 到 いた 身上 しんじょう 任 にん 何 なん 点 てん 的 てき 直 ちょく 都 と 可 か 表示 ひょうじ (详见欧 おう 拉 ひしげ 角 かく 因 よし 存在 そんざい 使 つかい 得 とく 每次 まいじ 将 はた 球面 きゅうめん 成 なり 自身 じしん 族 ぞく 被 ひ 称 しょう 面 めん 是 ぜ 唯 ただ 点 てん 周 しゅう x y 和平 わへい 移 うつり 体 たい 是 ぜ 唯 ただ 旋转表面 ひょうめん 和 かず 螺旋 らせん 面 めん 是 ぜ 具有 ぐゆう 数 すう 系列 けいれつ 的 てき 表面 ひょうめん
演 えんじ 示 しめせ 工程 こうてい 的 てき 牌 ぱい 英 えい 格 かく 黑 くろ 桃 もも 球体 きゅうたい Albert, Abraham Adrian, Solid Analytic Geometry, Dover, 2016 [1949], ISBN 978-0-486-81026-3 Dunham, William. The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities. : 28, 226. ISBN 0-471-17661-3 Kreyszig, Erwin, Advanced Engineering Mathematics 3rd, New York: Wiley , 1972, ISBN 0-471-50728-8 Steinhaus, H., Mathematical Snapshots Third American, Oxford University Press, 1969 Woods, Frederick S., Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry, Dover, 1961 [1922]


























![{\displaystyle V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\right)={\frac {4}{3}}\pi r^{3}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c081de9760153a5ab7e59be1b9de1aa97d08dec)










![{\displaystyle A=\int _{0}^{2\pi }\mathrm {d} \theta \,\int _{0}^{\pi }r^{2}\sin {\varphi }\mathrm {d} \varphi =\int _{0}^{2\pi }[-r^{2}\cos {\varphi }]_{0}^{\pi }\,\mathrm {d} \theta =4\pi r^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a27c8ea81d50d501df7fb3bb0bff593f198ad3)




