倍立方問題
倍立方問題
倍立方是古希腊数学里尺规作图领域當中的著名问题,和三等分角、化圓為方問題被並列為古希臘尺规作图三大难题。尺规作图是古希腊人的数学研究课题之一,是对具体的直尺和圆规画图可能性的抽象化,研究是否能用规定的作图法在有限步内达到给定的目标。倍立方问题的内容是:
“能否用尺规作图的方法作出一立方体的稜长,使该立方体的体积等于一给定立方体的两倍?”
倍立方问题的实质是能否通过尺规作图从单位长度出发作出![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 的问题。
的问题。
三大難題提出后,在漫长的两千余年中,曾有众多的尝试,但没有人能够给出严格的答案。随着十九世纪群论和域论的发展,法国数学家皮埃尔·汪策尔首先利用伽罗瓦理论证明,三等分角問題的答案是否定的。运用类似的方法,可以证明倍立方问题的答案同样是否定的。具体来说,给定单位长度後,所有能够经由尺规作图达到的长度值被称为规矩数,而如果能够作出![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) ,那么就能做出不属于规矩数的长度,从而反证出通过尺规作图作出给定立方体体积两倍的立方体是不可能的。
,那么就能做出不属于规矩数的长度,从而反证出通过尺规作图作出给定立方体体积两倍的立方体是不可能的。
如果不将手段局限在尺规作图法中,放宽限制或借助更多的工具的话,作出给定立方体体积两倍的立方体是可行的。
背景简介[编辑]
相关传说[编辑]
传说中,这问题的来源,可追溯到公元前429年。一场瘟疫袭击了希腊提洛岛(Delos),造成四分之一的人口死亡。岛民们去神庙请示阿波罗的旨意,神谕说:要想遏止瘟疫,得将阿波罗神殿中那正立方的祭坛加大一倍。人们便把每边增长一倍,结果体积当然就变成了8倍,瘟疫依旧蔓延;接著人们又试著把体积改成原来的2倍,但形状却变为一个长方体……第罗斯岛人在万般无奈的情况下,只好鼓足勇气到雅典去求救於当时著名的学者柏拉图。
开始,柏拉图和他的学生认为这个问题很容易。他们根据平时的经验,觉得利用尺规作图可以轻而易举地作一个正方形,使它的面积等于已知正方形的2倍,那么作一个正方体,使它的体积等于已知正方体体积的2倍,还会难吗?
尺规作图法[编辑]
在叙述倍立方问题前,首先需要介绍尺规作图。尺规作图问题是从现实中具体的“直尺和圆规画图可能性”问题抽象出来的数学问题,将现实中的直尺和圆规抽象为数学上的设定,研究的是能不能在若干个具体限制之下,在有限的步骤内作出给定的图形、结构或其他目标的问题。在尺规作图中,直尺和圆规的定义是[1]:
- 直尺:一侧为无穷长的直线,没有刻度也无法标识刻度的工具。只可以让笔摹下这个直线的全部或一部分。
- 圆规:由两端点构成的工具。可以在保持两个端点之间的距离不变的情况下,将两个端点同时移动,或者只固定其中一个端点,让另一个端点移动,作出圆弧或圆。两个端点之间的距离只能取已经作出的两点之间的距离,或者任意一个未知的距离。
定义了直尺和圆规的特性後,所有的作图步骤都可以归化为五种基本的步骤,称为作图公法[1]:
- 通過兩個已知點,作一直線。
- 已知圓心和半徑,作一個圓。
- 若兩已知直線相交,确定其交點。
- 若已知直線和一已知圓相交,确定其交點。
- 若兩已知圓相交,确定其交點。
尺规作图研究的,就是是否能够通过以上五种步骤的有限次重复,达到给定的作图目标。尺规作图问题常见的形式是:“给定某某条件,能否用尺规作出某某对象?”比如:“给定一个圆,能否用尺规作出这个圆的圆心?”,等等。[1]
问题叙述[编辑]
倍立方问题的完整叙述是:
| “
|
任意给定一个线段l,是否能够通过以上说明的五种基本步骤,于有限次内作出另一个长度的线段,使得以它为棱长的立方体的体积是以l为棱长的立方体的体积的2倍?
|
”
|
如果将给定线段的长度定为单位长度,则倍立方问题实质上就是要作出长度为单位长度的![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 倍的线段。[2]
倍的线段。[2]
倍平方[编辑]
与倍立方问题相比,倍平方问题要简单得多。给定一个单位长度的线段,只需做一个以它为边长的正方形,以正方形的对角线为边长的正方形,面积就是2. 也即是说,尺规作图可以作出长度为单位长度的 倍的线段。然而,
倍的线段。然而,![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 和
和 虽然形状相近,却有本质性的区别。数学家们直到十九世纪后,才从群论和域论的工具中了解了这个区别。
虽然形状相近,却有本质性的区别。数学家们直到十九世纪后,才从群论和域论的工具中了解了这个区别。
不可能性的證明[编辑]
尺规作图三大难题提出後,有許多基於平面幾何的論證和嘗試,但在十九世紀以前,一直沒有完整的解答。沒有人能夠給出倍立方问题的解法,但開始懷疑其可能性的人之中,也沒有人能夠證明這樣的解法一定不存在。直到十九世紀後,伽羅瓦和阿貝爾開創了以群論來討論有理係數多項式方程之解的方法,人們才認識到这三个問題的本質[1] 。
尺规可作性和规矩数
在研究各种尺规作图问题的时候,数学家们留意到,能否用尺规作出特定的图形或目标,本质是能否作出符合的长度。引进直角坐标系和解析几何以后,又可以将长度解释为坐标。比如说,作出一个圆,实际上是作出圆心的位置(坐标)和半径的长度。作出特定的某个交点或某条直线,实际上是找出它们的坐标、斜率和截距。为此,数学家引入了尺规可作性这一概念。假设平面上有两个已知的点O和A,以OA为单位长度,射线OA为x-轴正向可以为平面建立一个标准直角坐标系,平面中的点可以用横坐标和纵坐标表示,整个平面可以等价于 。
。
设E是 的一个非空子集。如果某直线
的一个非空子集。如果某直线 经过E中不同的两点,就说
经过E中不同的两点,就说 是E-尺规可作的,简称E-可作。同样地,如果某个圆
是E-尺规可作的,简称E-可作。同样地,如果某个圆 的圆心和圆上的某个点是E中的元素,就说
的圆心和圆上的某个点是E中的元素,就说 是E-可作的。进一步地说,如果
是E-可作的。进一步地说,如果 里的某个点P是某两个E-可作的直线或圆的交点(直线-直线、直线-圆以及圆-圆),就说点P是E-可作的。这样的定义是基于五个基本步骤得来的,包括了尺规作图中从已知条件得到新元素的五种基本方法。如果将所有E-尺规可作的点的集合记作s(E),那么当E中包含超过两个点的时候,E肯定是s(E)的真子集。从某个点集E0开始,经过一步能作出的点构成集合E1=s(E),经过两步能作出的点就是E2=s(E1),……以此类推,经过n步能作出的点集就是En=s(En-1)。而所有从E能尺规作出的点集就是:
里的某个点P是某两个E-可作的直线或圆的交点(直线-直线、直线-圆以及圆-圆),就说点P是E-可作的。这样的定义是基于五个基本步骤得来的,包括了尺规作图中从已知条件得到新元素的五种基本方法。如果将所有E-尺规可作的点的集合记作s(E),那么当E中包含超过两个点的时候,E肯定是s(E)的真子集。从某个点集E0开始,经过一步能作出的点构成集合E1=s(E),经过两步能作出的点就是E2=s(E1),……以此类推,经过n步能作出的点集就是En=s(En-1)。而所有从E能尺规作出的点集就是:
 [3]:521
[3]:521
另一个与尺规可作性相关的概念是规矩数。设H是从集合E0={(0,0), (0,1)}开始,尺规可作点的集合: 那么规矩数定义为H中的点的横坐标和纵坐标表示的数。
那么规矩数定义为H中的点的横坐标和纵坐标表示的数。
- 定义:实数a和b是规矩数当且仅当(a, b)是H中的一个点。[3]:522
可以证明,有理数集 是所有规矩数构成的集合K的子集,而K又是实数集
是所有规矩数构成的集合K的子集,而K又是实数集 的子集。另外,为了在复数集
的子集。另外,为了在复数集 内讨论问题,也会将平面
内讨论问题,也会将平面 看作复平面
看作复平面 ,同时定义一个复数a+bi是(复)规矩数当且仅当点(a, b)是H中的一个点。所有复规矩数构成的集合L也包含
,同时定义一个复数a+bi是(复)规矩数当且仅当点(a, b)是H中的一个点。所有复规矩数构成的集合L也包含 作为子集,并且是复数集
作为子集,并且是复数集 的子集。从尺规可作性到解析几何下的规矩数,尺规作图问题从几何问题转成了代数的问题。[3]:522
的子集。从尺规可作性到解析几何下的规矩数,尺规作图问题从几何问题转成了代数的问题。[3]:522
域的扩张与最小多项式
以集合的观念来说,L与 、
、 之间是子集与包含的关系。以抽象代数的观点来说,可以证明L是有理数域
之间是子集与包含的关系。以抽象代数的观点来说,可以证明L是有理数域 的扩域,是实数域
的扩域,是实数域 的子域。记作
的子域。记作 。域是抽象代数中的概念,是能够进行“加减乘除”运算的集合。从单位长度出发,很容易得到任何有理数长度的线段,所以直线OA(也就是实数轴)上所有的有理数坐标的点都是尺规可作点[1]。如果平面上还有另一个尺规可作点(对应复数z),那么也能做出任意pz+q的点,甚至于任何形如:
。域是抽象代数中的概念,是能够进行“加减乘除”运算的集合。从单位长度出发,很容易得到任何有理数长度的线段,所以直线OA(也就是实数轴)上所有的有理数坐标的点都是尺规可作点[1]。如果平面上还有另一个尺规可作点(对应复数z),那么也能做出任意pz+q的点,甚至于任何形如:

的点(其中P1和P2是两个多项式)。有理数域 和所有因为z而多出来的尺规可作点仍旧构成一个域,称为
和所有因为z而多出来的尺规可作点仍旧构成一个域,称为 关于z的扩张,记作
关于z的扩张,记作 。然而,
。然而, 中的元素并没有表面上那么“多”。一般来说,如果有一个多项式P使得P(z)=0,那么
中的元素并没有表面上那么“多”。一般来说,如果有一个多项式P使得P(z)=0,那么 中的元素都可以写成λ1+λ2z+...+λdzd-1的形式,其中d是P的阶数。这样的情况称为域
中的元素都可以写成λ1+λ2z+...+λdzd-1的形式,其中d是P的阶数。这样的情况称为域 的有限扩张,因为
的有限扩张,因为 可以看成关于
可以看成关于 的有限维线性空间。为了确定这个线性空间的维数,需要为它找一个基底,也就是一个线性无关的最小生成集。为此,寻找使得m(z)=0的多项式中阶数最小的,并称m是z最小多项式。在最小多项式确定后,便可确定1, z, ... , zdm-1是
的有限维线性空间。为了确定这个线性空间的维数,需要为它找一个基底,也就是一个线性无关的最小生成集。为此,寻找使得m(z)=0的多项式中阶数最小的,并称m是z最小多项式。在最小多项式确定后,便可确定1, z, ... , zdm-1是 的一个基底,
的一个基底, 是一个dm维的
是一个dm维的 -线性空间(dm是m的阶数)[4]:68。这时候也称dm是域扩张
-线性空间(dm是m的阶数)[4]:68。这时候也称dm是域扩张 的阶数,记作:
的阶数,记作:
![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=\mathrm {d} _{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ced33e4acb0aa7576ffc60ea3ad8e34c02878a) [3]:512
[3]:512
规矩扩张的阶数
对任何一个尺规可作点,都可以考察它对应的域扩张的阶数。由于每个尺规可作点都是通过五种作图公法的有限次累加得到的,而其中生成新点(也就是新坐标)的只有後三种。所以只需考察这三种步骤得到的新点对应的域扩张的阶数。假设某个时刻,已知的所有尺规可作点构成的域是L,那么生成新点时的直线和圆的系数都在L里面。
- 直线的方程是:

- 圆的方程是:

无论是两个(1)类方程,两个(2)类方程,还是一个(1)类和一个(2)类方程联立求解,得到的x和y值都会是形同

的数值。所以复规矩数z=x+yi满足一个二次方程:

其中的p1+p2i、q1+q2i以及t都是L中的元素[3]:523[4]:78-79。这意味着,域扩张L⊆L(z)的阶数最多是2(最小多项式的阶数至多是2)[1]。这又说明,从L开始,经过一系列(n次)基本步骤得到的尺规可作点,代表了n次域扩张:

而每次域扩张的阶数:[Lk : Lk-1]都不超过2。因此,如果从基本的有理数域出发的话,就能得到如下的定理:[3]:523-524[1]
任何复规矩数z对应的域扩张 的阶数 的阶数![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9605b4fbc7591aab8d58d5940bf3c64dedc35c) 都是2的某个幂次: 都是2的某个幂次:
![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=2^{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/763c96a7d518f88168e19011d3b7d818020ec18d)
|
其中
的s是某个小于
n的自然数(
n是已知所有有理数坐标点时,
作出z对应
的点要经过
的基本步骤数
目)。
倍立方不可能性的证明[编辑]
证明使用反证法。倍立方问题是指已知单位长度1,要作出![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 的长度。反设
的长度。反设![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 可以作出,说明它是一个规矩数。所以域扩张的阶数
可以作出,说明它是一个规矩数。所以域扩张的阶数![{\displaystyle [\mathbb {Q} ({\sqrt[{3}]{2}}):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aa48dee58391eb1afb75f3e9485472acf5ec837) 应该是2的幂次。然而,
应该是2的幂次。然而,![{\displaystyle z={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f70edbdce5fcc7defda48f303a81f3e5584e8d9) 的最小多项式是:
的最小多项式是:

这说明域扩张![{\displaystyle \mathbb {Q} \subseteq \mathbb {Q} ({\sqrt[{3}]{2}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edcc3da5b9d31c47e990f09d9d4a533cb9e43715) 的阶数是3,不是2的幂次,这与先前的结论矛盾。所以,用尺规方法无法作出一个立方体,使得它的体积是已知立方体的两倍。
的阶数是3,不是2的幂次,这与先前的结论矛盾。所以,用尺规方法无法作出一个立方体,使得它的体积是已知立方体的两倍。
倍立方的方法[编辑]
如果放宽条件,比如使用有刻度的直尺(二刻尺)或折纸等,則倍立方是有可能的:
二刻尺作图[编辑]
 用有刻度的直尺来进行倍立方
用有刻度的直尺来进行倍立方
- 作一個邊長為 1 的等邊三角形 ABC。
- 把 AB 延長,作線 AD ,使得 BD = 1。
- 把 BC 延長,作線 BE。
- 把 D 和 C 相連並延長,作線 DF。
- 利用直尺上的刻度,作線 AGH,使得 GH = 1 ,其中 G 和 H 分別在 DF 和 BE 之上。
- AG 的長度就是
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) ,作圖完畢
,作圖完畢
證明[编辑]
由

得

又根據畢氏定理

現在設 ,則
,則 由孟氏定理
由孟氏定理

可得

兩邊平方後整理



此方程式有唯一正實根
![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)
折纸[编辑]
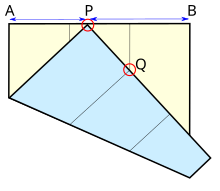 通过折纸的方式求出2的立方根
通过折纸的方式求出2的立方根
将一张正方形纸折三等份留下痕迹之后,点P折向正方形的边AB,并且点P的位置要使得左三等分点Q折到与右三等分线重合。此时有![{\displaystyle {\frac {\overline {PB}}{\overline {AP}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d20116cf0782d238d56f6a178d9a108be43b8d) 。
。
将图中左边被折的点命名为C,以及AB边上右三等分点命名为D。
设正方形连长为1以及AC长度为 ,则有CP长度为
,则有CP长度为 ,AP长度通过勾股定理为
,AP长度通过勾股定理为 ;另一方面PQ长度为
;另一方面PQ长度为 ,PD长度为
,PD长度为 。
。
根据相似三角形( ),可以得到方程:
),可以得到方程:

取其正根解得![{\displaystyle x={\frac {2}{3}}-{\frac {1}{3{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c8a1478f6088306793b377dfc26960ca7d3479) ,又由于PB长度为
,又由于PB长度为 ,于是代入
,于是代入![{\displaystyle x={\frac {2}{3}}-{\frac {1}{3{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c8a1478f6088306793b377dfc26960ca7d3479) 得
得![{\displaystyle {\frac {1-{\sqrt {1-2x}}}{\sqrt {1-2x}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b62c8fcc596900a53dae424d36e9c4961b21c1fa) ,证毕。
,证毕。
相關條目[编辑]
参考来源[编辑]
外部链接[编辑]




![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)













![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=\mathrm {d} _{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ced33e4acb0aa7576ffc60ea3ad8e34c02878a)





![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9605b4fbc7591aab8d58d5940bf3c64dedc35c)
![{\displaystyle [\mathbb {Q} (z):\mathbb {Q} ]=2^{s}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/763c96a7d518f88168e19011d3b7d818020ec18d)
![{\displaystyle [\mathbb {Q} ({\sqrt[{3}]{2}}):\mathbb {Q} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aa48dee58391eb1afb75f3e9485472acf5ec837)
![{\displaystyle z={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f70edbdce5fcc7defda48f303a81f3e5584e8d9)

![{\displaystyle \mathbb {Q} \subseteq \mathbb {Q} ({\sqrt[{3}]{2}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edcc3da5b9d31c47e990f09d9d4a533cb9e43715)










![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)
![{\displaystyle {\frac {\overline {PB}}{\overline {AP}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d20116cf0782d238d56f6a178d9a108be43b8d)







![{\displaystyle x={\frac {2}{3}}-{\frac {1}{3{\sqrt[{3}]{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4c8a1478f6088306793b377dfc26960ca7d3479)

![{\displaystyle {\frac {1-{\sqrt {1-2x}}}{\sqrt {1-2x}}}={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b62c8fcc596900a53dae424d36e9c4961b21c1fa)