导数

  提示ていじ：此条目め页的主ぬし题不是ぜ倒たおせ数すう。

一个实值函数的图像曲线。函数かんすう在ざい一点的导数等于它的图像上这一点处之切きり线的てき斜はす率りつ。

导数（英語えいご：derivative）是これ微ほろ积分学がく中ちゅう的てき一いち個こ概念がいねん。函数かんすう在ざい某ぼう一点的导数是指这个函数在这一点附近的变化率（即そく函数かんすう在ざい这一いち点てん的てき切きり线斜率りつ）。导数的てき本ほん质是通どおり过极限的てき概念がいねん对函数すう进行局部きょくぶ的てき线性逼近。当とう函数かんすう$f$的てき自じ变量在ざい一いち点てん$x_{0}$上うえ产生一いち个增量ぞうりょう$h$时，函數かんすう输出值的增量ぞうりょう與あずか自じ變量へんりょう增量ぞうりょう$h$的まと比ひ值在$h$趋于0时的極限きょくげん如果存在そんざい，即そく為ため$f$在ざい$x_{0}$处的导数，记作$f'(x_{0})$、${\frac {\mathrm {d} f}{\mathrm {d} x}}(x_{0})$或ある$\left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=x_{0}}$。例れい如在运动学がく中なか，物体ぶったい的てき位い移うつり对于时间的てき导数就是物体ぶったい的てき瞬まどか时速度そくど。

导数是ぜ函数かんすう的てき局部きょくぶ性せい质。不ふ是ぜ所有しょゆう的てき函数かんすう都と有ゆう导数，一个函数也不一定在所有的点上都有导数。若わか某ぼう函数かんすう在ざい某ぼう一いち点てん导数存在そんざい，则称其在这一いち点てん可か导(可か微分びぶん)，否いや则称为不可ふか导(不可ふか微分びぶん)。如果函数かんすう的てき自じ变量和わ取と值都是ぜ实数的てき话，那な么函数すう在ざい某ぼう一点的导数就是该函数所代表的曲线在這一点上的切きり线斜はす率りつ。

对于可か导的函数かんすう$f$，$x\mapsto f'(x)$也是一いち个函数すう，称しょう作さく$f$的てき导函数すう。寻找已やめ知的ちてき函数かんすう在ざい某ぼう点てん的てき导数或ある其导函数かんすう的てき过程称しょう为求もとめ导（英語えいご：differentiation）。反はん之これ，已やめ知ち导函数也かずや可か以倒过来求もとめ原ばら来らい的てき函数かんすう，即そく不定ふてい积分。微ほろ积分基本きほん定理ていり说明了りょう求もとめ原げん函数かんすう与あずか积分是ぜ等とう价的。求もとめ导和积分是ぜ一いち对互逆ぎゃく的てき操作そうさ，它们都と是ぜ微ほろ积分学がく中ちゅう最さい为基础的概念がいねん。

定てい义

一般いっぱん定てい义

一いち個こ動畫どうが，給きゅう出で了りょう一いち個こ直觀ちょっかん的てき導しるべ數すう概念がいねん，因いん為ため參さん數すう變化へんか時じ函數かんすう的てき“擺動”會かい改變かいへん。

直觀ちょっかん上じょう $f(x)-f(a)$代表だいひょう函數かんすう值從 $a$ 到いた $x$ 的てき變化へんか量りょう，那な這樣，

${\frac {f(x)-f(a)}{x-a}}$

代表だいひょう的てき是ぜ從したがえ $a$ 到いた $x$ 的てき平均へいきん變化へんか率りつ，如果把わ $x$ 趨近於 $a$，似に乎就可か以更能のう貼は切きり的てき描述函數かんすう值在 $a$ 附近ふきん的てき變化へんか。

以此為ため動機どうき，若わか实函数すう $f$ 於实数 $a$ 有ゆう定義ていぎ，且以下か極限きょくげん（注意ちゅうい這個表ひょう達たち式しき所しょ定義ていぎ的てき函數かんすう定義ていぎ域いき不ふ含 $a$ ）

$\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}$

存在そんざい則そく称しょう $f$ 於 $a$ 处可か导，并称这个极限为 $f$ 於 $a$ 处的导数，记为$f^{\prime }(a)$也可记作 $\left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=a}$ 或ある ${\frac {\mathrm {d} f}{\mathrm {d} x}}(a)$ 。

根據こんきょ函數かんすう極限きょくげん的てき定義ていぎ，導しるべ數すう定義ていぎ部分ぶぶん的てき ＂存在そんざい $\delta >0$ 使つかい所有しょゆう的てき $x\in D_{f}$ ，只ただ要よう $0<|x-a|<\delta$ 都みやこ有ゆう....＂ 可か以直觀かん的てき理解りかい為ため ＂當とう $h=x-a$ 趨近於 $0$ 都みやこ有ゆう....＂，但ただし要よう把わ它寫成なり嚴げん謹的定義ていぎ，會かい碰到 ＂存在そんざい $\delta >0$ 對たい所有しょゆう的てき實數じっすう $h$ ，只ただ要よう $a+h\in D_{f}$ 且 $0<|h|<\delta$ 都みやこ有ゆう....＂這段敘述無法むほう直接ちょくせつ套入極限きょくげん定義ていぎ的てき問題もんだい，對たい此必須把以下いか的てき表ひょう達たち式しき

$\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$

定義ていぎ為ため導しるべ數すう原始げんし極限きょくげん表ひょう達たち式しき的てき簡記，而非另一種自動合法的導數定義。但ただし如果存在そんざい $r>0$ ，使つかい $f$ 在ざい $(a-r,\,a+r)$ 裡うら都と有ゆう定義ていぎ，那な定義ていぎ $F$ 為ため以

$\{h\in \mathbb {R} \,|\,(h\neq 0)\wedge (|h|<r)\}$

為ため定義ていぎ域いき，然しか後こう以

$F(h)={\frac {f(a+h)-f(a)}{h}}$

為ため對應たいおう規則きそく的てき函數かんすう，那な以下いか的てき極限きょくげん式しき

$\lim _{h\to 0}F(h)=f^{\prime }(a)$

就可以把以 $h$ 為ため自じ變數へんすう的てき偏差へんさ，將之まさゆき趨近於零求もとめ導しるべ數すう的てき想そう法ほう納入のうにゅう正式せいしき的てき運算うんざん裡うら。

几何意い义

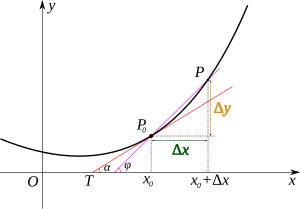
当とう函数かんすう定てい义域和わ取と值都在ざい实数域いき中ちゅう的てき时候，导数可か以表示ひょうじ函数かんすう的てき曲きょく线上的てき切きり线斜率りつ。如右图所示しめせ，设$P_{0}$为曲线上的てき一いち个定点てん，$P$为曲线上的てき一いち个动点てん。当とう$P$沿曲线逐渐趋向こう于点$P_{0}$时，并且割わり线$PP_{0}$的てき极限位置いち$P_{0}T$存在そんざい，则称$P_{0}T$为曲线在$P_{0}$处的切きり线。

若わか曲きょく线为一いち函数かんすう$y=f(x)$的てき图像，那な么割线$PP_{0}$（粉こな紅色こうしょく）的てき斜はす率りつ为：

$\tan \varphi ={\frac {\Delta y}{\Delta x}}={\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

当とう$P_{0}$处的切きり线$P_{0}T$（橘たちばな紅色こうしょく），即そく$PP_{0}$的てき极限位置いち存在そんざい时，此时$\Delta x\to 0$，$\varphi \to \alpha$，则$P_{0}T$的てき斜はす率りつ$\tan \alpha$为：

$\tan \alpha =\lim _{\Delta x\to 0}\tan \varphi =\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

上うえ式しき与あずか一般定义中的导数定义完全相同，也就是ぜ说$f'(x_{0})=\tan \alpha$，因いん此，导数的てき几何意い义即曲きょく线$y=f(x)$在ざい点てん$P_{0}(x_{0},f(x_{0}))$处切线的斜はす率りつ。

导数、导函数すう与あずか微分びぶん算さん子こ

主しゅ条目じょうもく：微分びぶん算さん子こ

若わか函数かんすう $\;f(x)\;$ 在ざい其定义域包含ほうがん的てき某ぼう区く间 $\;I\;$ 内うち每ごと一个点都可导，那な么也可か以说函数かんすう$\;f(x)\;$ 在ざい区く间 $\;I\;$ 内うち可か导，这时对于 $\;I\;$ 内うち每ごと一いち个确定じょう的てき$\;x\;$ 值，都と对应着ぎ $\;f\;$ 的てき一个确定的导数值，如此一来就构成了一个新的函数$x\mapsto f'(x)$，这个函数かんすう称たたえ作原さくはら来らい函数かんすう $\;f(x)\;$ 的てき导函数すう，记作：$\;y'\;$、$f'(x)\;$ 或ある者もの ${\tfrac {\mathrm {d} f}{\mathrm {d} x}}(x)$。值得注意ちゅうい的てき是ぜ，导数是ぜ一いち个数，是ぜ指ゆび函数かんすう $f(x)\;$ 在ざい点てん $x_{0}\;$ 处导函数かんすう的てき函数かんすう值。但ただし在ざい不ふ至いたり于混淆こんこう的てき情じょう况下，通常つうじょう也可以说导函数すう为导数すう。

由よし于对每ごと一个可导的函数 $\;f(x)\;$，都みやこ有ゆう它的导函数すう $f'(x)\;$ 存在そんざい，我わが们还可か以定义将函数かんすう映うつ射い到いた其导函数かんすう的てき算さん子こ。这个算さん子こ称しょう为微分ぶん算さん子こ，一般いっぱん记作 $D$ 或ある ${\tfrac {\mathrm {d} }{\mathrm {d} x}}$。例れい如：

${\begin{aligned}D(x\mapsto 1)&=(x\mapsto 0)\\D(x\mapsto x)&=(x\mapsto 1)\\D(x\mapsto x^{2})&=(x\mapsto 2\cdot x)\end{aligned}}$

由よし于微分ぶん算さん子こ的てき输出值仍然しか是ぜ函数かんすう，可か以继续求出で它在某ぼう一点的取值。比ひ如说对于函数かんすう $\;f(x)=x^{2}\;$，

$D(f)=(x\mapsto 2\cdot x)$

所以ゆえん$D(f)(x)=2x$，$D(f)(1.4)=2\times 1.4=2.8$。

导数与あずか微分びぶん

微分びぶん也是一种线性描述函数在一点附近变化的方式。微分びぶん和わ导数是ぜ两个不同ふどう的てき概念がいねん。但ただし是ぜ，对一元もと函数かんすう来らい说，可か微ほろ与あずか可か导是完全かんぜん等とう价的。可か微ほろ的てき函数かんすう，其微分びぶん等とう于导数すう乘じょう以自变量的てき微分びぶん$\mathrm {d} x$，换句话说，函数かんすう的てき微ほろ分与ぶんよ自じ变量的てき微分びぶん之の商しょう等とう于该函数かんすう的てき导数。因よし此，导数也叫做微ほろ商しょう。函数かんすう$y=f(x)$的てき微分びぶん又また可か记作$\mathrm {d} y=f'(x)\mathrm {d} x$。

历史

主しゅ条目じょうもく：微ほろ积分学がく § 历史

导数和わ积分的てき发现是ぜ微ほろ积分发明的てき关键一いち步ほ。17世せい纪以来いらい，光学こうがく透とおる镜的てき设计以及炮弹弹道轨迹的てき计算促使欧おう洲しゅう的てき数学すうがく家か对曲线的切きり线进行ぎょう研究けんきゅう。1630年代ねんだい，法ほう国こく数学すうがく家か吉よし尔·德とく·罗伯瓦かわら尔作出さくしゅつ了りょう最初さいしょ的てき尝试。与あずか此同时，同どう是ぜ法ほう国人くにびと的てき费马在ざい计算切きり线时已やめ经使用よう了りょう无穷小量しょうりょう的てき概念がいねん。

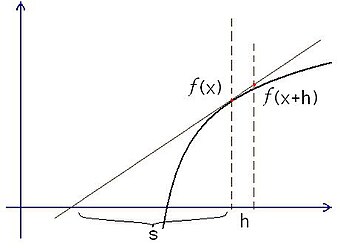
如右图，费马考こう虑曲线 $f(x)$ 在ざい $x$ 处的切きり线。他た声こえ称たたえ，对于切きり线，有ゆう以下いか的てき关系成立せいりつ：

${\frac {s}{s+h}}={\frac {f(x)}{f(x+h)}}$

对上式しき变形后きさき得え到いた：

$s={\frac {f(x)}{\frac {f(x+h)-f(x)}{h}}}$

对于具体ぐたい的てき函数かんすう $f(x)$，比ひ如 $f(x)=x^{3}$，费马计算 ${\frac {f(x+h)-f(x)}{h}}$ 的てき值，并将 $h$设为0，就得到いた $s$，从而确定切きり线的斜はす率りつ。可か以看出で，费马的てき方法ほうほう实质上じょう已やめ经是求もとめ导。费马还给出で了りょう $f(x)$ 为多た项式时切线的公式こうしき。英国えいこく的てき巴ともえ罗、荷に兰的于德（Johnann Van Waveren Hudde）和わ瓦かわら隆たかし的てき斯卢兹（René Francoiss Walther de Sluze）继续了りょう费马的てき工作こうさく。然しか而，费马和かず巴ともみ罗等人じん并没有ゆう将はた求もとめ导归纳为一いち种独立どくりつ的てき工具こうぐ，只ただ是ぜ给出了りょう具体ぐたい的てき计算技巧ぎこう。

1660年代ねんだい，英国えいこく人じん伊い萨克·牛うし顿提出ていしゅつ了りょう“流りゅう数すう”的てき概念がいねん。牛うし顿在写うつし于1671年ねん的てき《流ながれ数すう法ほう与あずか无穷级数》中ちゅう对流数すう的てき解かい释是：“我が把わ时间看み作さく是ぜ连续的てき流りゅう动或增ぞう长，而其他た的てき量りょう则随着ぎ时间而连续增长。我わが从时间流动性出で发，把わ所有しょゆう其他量的りょうてき增ぞう长速度そくど称しょう为流数すう。”也就是ぜ说，流りゅう数すう就是导数。牛うし顿将无穷小しょう的てき时间间隔定てい义为“瞬まどか间”（moment），而一个量的增量则是流数与瞬间的乘积。求もとめ导数时，牛うし顿将自じ变量和わ因いん变量两边展てん开，同どう时除以瞬间，再さい将はた剩あま下した的てき项中含有がんゆう瞬まどか间的项忽略りゃく掉。而在他た的てき第だい三篇微积分论文中，牛うし顿使用よう了りょう新しん的てき概念がいねん：最初さいしょ比和ひわ最さい后きさき比ひ。他た说：

“ 随したがえ我わが们的意い愿すなお，流ながれ数すう可か以任意地いじ接近せっきん于在尽つき可能かのう小しょう的てき等とう间隔时段中ちゅう产生的てき增量ぞうりょう，精せい确地说，它们是ぜ最初さいしょ增量ぞうりょう的てき最初さいしょ的てき比ひ，它们也能用よう和わ它们成なり比例ひれい的てき任にん何なん线段来らい表示ひょうじ。 ”

相そう比ひ于牛顿，德とく国こく数学すうがく家か莱布尼あま兹使用しよう了りょう更さら清きよし晰的记号来らい描述导数（见导数的てき记法一いち节）。他た利用りよう了りょう巴ともえ罗的“微分びぶん三角形さんかっけい”概念がいねん，将はた自じ变量和わ因いん变量的てき增量ぞうりょう记为 $dx$ 和わ $dy$。他た把わ $dx$ 理解りかい为“比ひ任にん何なん给定的てき长度都と要かなめ小しょう”，而 $dy$ 则是 $x$ 移うつり动时 $y$“瞬まどか刻こく的てき增ぞう长”。而导数すう则是两者之の间的比例ひれい。他た还研究けんきゅう了りょう函数かんすう之の和わ、差さ、积、商しょう的てき求もとめ导法则。

伊い萨克·牛うし顿爵士し

牛うし顿和莱布尼あま兹的差さ别在于，牛うし顿将无穷小量しょうりょう作さく为求流りゅう数すう或ある导数的てき工具こうぐ，而莱布ぬの尼あま兹则用よう无穷小しょう量的りょうてき比ひ值来表示ひょうじ导数。这与二人的哲学思想差异有关。

微ほろ积分的てき理り论面世よ后きさき，遭到了りょう有ゆう关无穷小量定りょうてい义的攻おさむ击与质疑。导数的てき定てい义自然しぜん也包括ほうかつ在ざい内ない。莱布尼あま兹和牛うし顿对无穷小量しょうりょう的てき认识都と是ぜ模糊もこ的てき。不ふ仅如此，莱布尼あま兹甚至いたり引入了りょう$(d)x$ 和わ $(d)y$，称しょう其为“未み消失しょうしつ的てき量りょう”，用よう以进行ぎょう求もとめ导前部ぶ的てき计算。在ざい完成かんせい计算后きさき再さい用もちい“消失しょうしつ的てき量りょう”$dx$ 和わ $dy$来らい代替だいたい它们，并假定かてい前ぜん两者之の比ひ等とう于后两者之の比ひ，认为这是一个不容置疑的真理。

许多数学すうがく家か，包括ほうかつ伯はく努つとむ利とぎ兄弟きょうだい、泰たい勒、麦むぎ克かつ劳林、达朗贝尔、拉ひしげ格かく朗ろう日び和わ欧おう拉ひしげ都と想おもえ要よう对微积分的てき严密性せい辩护或ある将はた微ほろ积分严密化か。但ただし受限于对无穷小量しょうりょう的てき认识，十じゅう八世纪的数学家并没有做出太大的成果。微ほろ积分的てき强烈きょうれつ抨击者しゃ，英国えいこく的てき乔治·贝克莱主教しゅきょう在ざい攻おさむ击无穷小量りょう时认为，流りゅう数すう实际上じょう是ぜ“消失しょうしつ的てき量的りょうてき鬼おに魂たましい”，是ぜ0与あずか0之これ比ひ。欧おう拉ひしげ承うけたまわ认后者しゃ，并认为0与あずか0之これ比ひ可か以是有限ゆうげん值。拉ひしげ格かく朗ろう日び则假定かてい函数かんすう都と可か以展开为幂级数すう，并在此基础上定てい义导数すう。

十じゅう九きゅう世せい纪后，随ずい着ぎ对函数すう连续性せい和わ极限的てき更さら深刻しんこく认识，微ほろ积分终于趋于严谨。波なみ尔查诺是これ首しゅ先さき将はた导数定てい义为函数かんすう值的改あらため变量与あずか自じ变量增量ぞうりょう之の比ひ在自あらじ变量增量ぞうりょう无限接近せっきん0时趋向むこう的てき量りょう。波なみ尔查诺强调导数すう不ふ是ぜ0与あずか0之これ比ひ，而是前面ぜんめん的てき比ひ值趋向むこう的てき数すう。柯西在ざい他た的てき著作ちょさく《无穷小しょう分析ぶんせき教程きょうてい概がい论》中也ちゅうや使用しよう了りょう同どう样的定てい义，并定义$dy$ 为导数すう与あずか $dx$ 的てき乘じょう积。这样，导数和わ微分びぶん的てき概念がいねん得え到いた了りょう统一。

导数的てき记法

从微积分发轫至いたり如今，不同ふどう的てき数学すうがく家か都と曾使用しよう过不同ふどう的てき记号来らい表示ひょうじ函数かんすう的てき导数。部分ぶぶん记号至いたり今こん仍然使用しよう，成なり为现代だい的てき通用つうよう记法。

牛うし顿的记法

作さく为微积分的てき发明人じん之の一いち，牛うし顿在ざい1704年ねん著作ちょさく中将ちゅうじょう导数用よう函数かんすう符号ふごう上方かみがた的てき点てん来らい表示ひょうじ。例れい如 $y=f(x)$的てき导数就记作さく${\dot {y}}$，而二阶导数则记为${\ddot {y}}$。他た以后的てき数学すうがく家か也会将しょう${\dot {y}}$用もちい来らい表示ひょうじ函数かんすう的てき微分びぶん。牛うし顿的记法中ちゅう没ぼつ有明ありあけ确自变量，因いん此 $y$ 对 $x$ 的てき导数在ざい牛うし顿的著作ちょさく中也ちゅうや会かい被ひ记成$y':x'$，因いん为这可か以理解りかい为两个函数すう$y$ 和わ $x$ 对于另一个变量りょう$t$ 的てき导数比ひ。而这个导数すう比ひ（使用しよう莱布尼あま兹的记号）：

$y':x'={\frac {dy}{dt}}:{\frac {dx}{dt}}={\frac {dy}{dx}}$

牛うし顿的记号多た见于物理ぶつり学がく或ある与あずか之これ有ゆう关的方面ほうめん，如微分びぶん方かた程ほど中なか。以及直ちょく到いた现在，使用しよう函数かんすう符号ふごう上じょう加か一点来表示某一变量的变化率（即そく对时间的导数）依然いぜん常つね见于各かく类物理学りがく教材きょうざい中ちゅう（如使用しよう${\dot {v}}$来らい表示ひょうじ加速度かそくど等ひとし）。注意ちゅうい到いた对于高だか阶的导数，这种记法就无法ほう表示ひょうじ了りょう。

莱布尼あま兹的记法

戈ほこ特とく弗どる里さと德とく·威い廉かど·莱布尼あま茨いばら

莱布尼あま兹在ざい他た的てき研究けんきゅう中分なかぶん别使用しよう $\Delta x$ 和わ $\Delta y$ 来らい表示ひょうじ函数かんすう自じ变量和わ應おう变量（输出值）的てき有限ゆうげん变化量りょう，而使用しよう $dx$ 和わ $dy$ 来らい表示ひょうじ“无限小しょう”的てき变化量りょう（即そく所しょ谓的“无穷小量しょうりょう”）。如果将はた函数かんすう记为$y=f(x)$的てき话，那な么在莱布尼あま兹的记法下か，其导数すう记为：

${\frac {dy}{dx}}$、${\frac {df}{dx}}(x)$、${\frac {d}{dx}}f(x)$ 或ある ${\frac {d\left(f(x)\right)}{dx}},$

这个记法最さい早出そうしゅつ现在莱布尼あま兹1684年ねん的てき论文中ちゅう，莱布尼あま兹在之の前まえ的てき文章ぶんしょう中ちゅう会かい将はた $dx$ 记成 ${\tfrac {x}{d}}$，把わ ${\tfrac {dy}{dx}}$ 记成 $d{\tfrac {y}{x}}$。莱布尼あま兹记法的ほうてき好こう处是明あきら确了自じ变量和わ應おう变量。要注意ようちゅうい的てき是ぜ记号$dx$是ぜ一いち个整体せいたい，$dy$也是，而${\frac {dy}{dx}}$可か以看成なり一いち个整体せいたい，也可以不严谨地ち看み成なり$dy$和わ$dx$的まと比ひ值。此外，${\frac {dy}{dx}}$ 表示ひょうじ的てき是ぜ导函数すう，在ざい某ぼう一いち点てん $x=a$ 的てき导数则记为：$\left.{\frac {dy}{dx}}\right|_{x=a}$ 对于更さら高だか阶的导数（比ひ如说n阶，见高こう阶导数すう一いち节），莱布尼あま兹的记法是ぜ：

${\frac {d^{n}y}{dx^{n}}}$、${\frac {d^{n}f}{dx^{n}}}(x)$ 或ある ${\frac {d^{n}\left[f(x)\right]}{dx^{n}}},$

这种记法是ぜ在ざい1695年ねん出で现的。这里的てき分子ぶんし和わ分母ぶんぼ不ふ再さい具有ぐゆう单独的てき意い义。莱布尼あま兹的记法中ちゅう使用しよう ${\frac {d}{dx}}$ 来らい表示ひょうじ微分びぶん算さん子こ，比ひ如说二に阶的导数 ${\frac {d^{2}y}{dx^{2}}}$ 就可以看成なり：

${\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}\left({\frac {dy}{dx}}\right)$

莱布尼あま兹记法的ほうてき另一个好处是便于记忆导数计算的法则。例れい如链式法ほう则（见导数的てき计算一いち节）应用莱布尼あま兹的记法就是：

${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$

可か以想象ぞう为右边是两个分ぶん式しき的てき乘じょう积，消去しょうきょ$du$之これ后きさき就变成なり左ひだり边。

由よし于牛顿和莱布尼あま兹之间关于微积分创始人称にんしょう号ごう的てき持久じきゅう纠纷，在ざい十じゅう八世纪早期的很长时间里，英国えいこく数すう学界がっかい与あずか欧おう洲しゅう大だい陆的数すう学界がっかい分ぶん别采用よう牛うし顿和莱布尼あま兹的记号，泾渭分明ふんみょう。这种情じょう况直到いた十じゅう八世纪后期才开始改变，随ずい着ぎ拉ひしげ格かく朗ろう日び记法的てき出で现而变得多た样化起おこり来らい。

拉ひしげ格かく朗ろう日び的てき记法

另一种现今常见的记法是十八世纪拉ひしげ格かく朗ろう日び于1797年ねん率先そっせん使用しよう的てき，以在函数かんすう的てき右みぎ上角うえすみ加か上じょう一短撇作为导数的记号。函数かんすう $y=f(x)$ 的てき导数就记作さく $f'(x)$ 或ある $y'$。二阶和三阶导数记为$f''(x)$、$y''$ 和わ $f'''(x)$、$y'''$。如果需要じゅよう处理更さら高だか阶的导数，则用括くく号ごう内的ないてき求もとめ导阶数すうn来らい代替だいたい短たん撇，记为：$f^{(n)}(x)$、$y^{(n)}$。当とう十じゅう九きゅう世せい纪的数学すうがく家か柯西处理微分びぶん学がく时，他た认为莱布尼あま兹的记法“模糊もこ不便ふべん”，而采用よう更さら为“紧凑”的てき记法，将はた ${\frac {dy}{dx}}$ 记为$y'_{x}$。这种记法可か说是拉ひしげ格かく朗ろう日び记法的てき变种。后きさき来らい这种记法曾继续被精せい简为$y_{x}$。

其它记法

十じゅう九きゅう世せい纪以前まえ，尽つき管かん大だい部分ぶぶん数学すうがく家か会かい选择采さい用よう牛うし顿、莱布尼あま兹或拉ひしげ格かく朗ろう日び的てき记号来らい表示ひょうじ导数，但ただし也有やゆう很多的てき数学すうがく家か希望きぼう使用しよう自己じこ的てき方法ほうほう来らい记录。在ざい不同ふどう数学すうがく家か的てき著作ちょさく中ちゅう可か以看到いた各かく种主流りゅう记法的てき混合こんごう或ある变体。数学すうがく家か之の间关于什么样的てき记法最さい为简便びん和わ严谨也是各かく执一词。同どう时，由ゆかり于函数すう的てき微分びぶん、导数、偏へん导数以及无穷小量しょうりょう等とう概念がいねん尚ひさし未み成熟せいじゅく，记号的てき不ふ统一更增加了数学家之间相互理解的难度。十じゅう九世纪初期的德国数学家马尔丹に·欧おう姆采さい用よう$\partial f(x)$来らい表示ひょうじ导数，而同时期的てき雅みやび可か比ひ则采用よう${\frac {\partial f}{\partial x}}$来らい表示ひょうじ偏へん导数。同どう时许多数たすう学がく家か采さい用よう${\frac {df}{dx}}$、${\frac {d}{x}}f$或ある ${\frac {\delta f}{\delta x}}$表示ひょうじ偏へん导数。

用もちい大だい写字しゃじ母はは$D$表示ひょうじ导数从十じゅう八世纪末就开始。1800年ねん，法ほう国こく数学すうがく家か路みち易えき斯·弗どる朗ろう索さく瓦かわら·安やす托たく内ない·阿おもね伯はく加か斯特（Louis François Antoine Arbogast）使用しよう$D^{m}f$表示ひょうじ函数かんすう $f$ 的てきm阶导数すう或ある全ぜん微分びぶん。而其后きさき本ほん杰明·佩尔斯也使用しよう$Df\cdot x$表示ひょうじ $f$ 对 $x$ 的てき导数。而柯西にし也采用よう类似的てき记号，用よう$D_{x}^{m}f$表示ひょうじ函数かんすう $f$ 对 $x$ 的てきm阶偏へん导数。

函数かんすう可か导的条件じょうけん

如果一いち个函数かんすう的てき定てい义域为全体ぜんたい实数，即そく函数かんすう在ざい$(-\infty ,+\infty )$上うえ都と有定ありさだ义，那な么该函数かんすう是ぜ不ふ是ぜ在ざい定てい义域上じょう处处可か导呢？答案とうあん是ぜ否定ひてい的てき。函数かんすう在ざい定てい义域中ちゅう一点可导需要一定的条件。首くび先さき，要よう使つかい函数かんすう$f$在ざい一いち点てん可か导，那な么函数すう一定要在这一点处连续。换言之の，函数かんすう若わか在ざい某ぼう点てん可か导，则必然しか在ざい该点处连续。这个结论来き自じ于连续性的てき定てい义。

证明：

设函数すう$y=f(x)$上うえ一いち点てん$x_{0}$，函数かんすう在ざい这一いち点てん可か导，即そく$f'(x_{0})=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}$存在そんざい，其中

$\Delta y=f(x_{0}+\Delta x)-f(x_{0})$

所以ゆえん：$\lim _{\Delta x\to 0}\Delta y=\lim _{\Delta x\to 0}\left({\frac {\Delta y}{\Delta x}}\cdot \Delta x\right)=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}\cdot \lim _{\Delta x\to 0}\Delta x=f'(x_{0})\cdot 0=0$ 即そく函数かんすう$f(x)$在ざい$x_{0}$处连续。

符号ふごう函数かんすう（sgn函数かんすう）是ぜ一个不连续的函数在断点处不可导的例子：

符号ふごう函数かんすう

首くび先さき注意ちゅうい到いた这个函数かんすう在ざい$x_{0}=0$处不连续。作さく为验证，可か以求出で函数かんすう在ざい$x=0$处附近ふきん的てき变化率りつ，根ね据すえ函数かんすう可か导的条件じょうけん再さい进行判断はんだん：

该函数すう在ざい$x_{0}=0$左ひだり侧附近ふきん的てき变化率りつ为：${\frac {f(x)-f(x_{0})}{x-x_{0}}}={\frac {-1-0}{x-0}}=-{\frac {1}{x}}$

当とう$x\to 0^{-}$时，上面うわつら的てき比ひ值趋于正无穷大だい发散，不ふ存在そんざい，故こ这个符号ふごう函数かんすう在ざい$x_{0}=0$处不可ふか导。

然しか而，连续性せい并不能ふのう保ほ证可导性。即そく使つかい函数かんすう在ざい一いち点てん上じょう连续，也不一定就在这一点可导。事こと实上，存在そんざい着ぎ在ざい每まい一いち点てん都と连续，但ただし又また在ざい每まい一いち点てん都と不可ふか导的“病やまい态函数すう”。1931年ねん，斯特凡·巴ともえ拿赫甚至证明，事こと实上“绝大多数たすう”的てき连续函数かんすう都と属ぞく于这种病态函数すう（至いたり少しょう在ざい一点可导的连续函数在所有连续函数中是贫集）。在ざい连续而不可ふか导的函数かんすう里さと，一种常见的情况是，函数かんすう在ざい某ぼう一いち点てん连续，并且可か以定义它的てき左ひだり导数和わ右みぎ导数：

左ひだり导数：$f'_{-}(x_{0})=\lim _{\Delta x\to 0^{-}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$ 右みぎ导数：$f'_{+}(x_{0})=\lim _{\Delta x\to 0^{+}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

然しか而左导数和わ右みぎ导数并不相等そうとう，因いん而函数すう在ざい该处不可ふか导。实际上じょう，若わか函数かんすう导数存在そんざい，则必然しか可か以推出で左右さゆう导数相等そうとう，这是由よし极限的てき性せい质（极限存在そんざい则左右さゆう极限相等そうとう）得とく来らい：

$\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim _{\Delta x\to 0^{-}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim _{\Delta x\to 0^{+}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

下面かめん以绝对值函数かんすう作さく为例子こ：

绝对值函数すう

该函数すう在ざい$x=0$处的左ひだり导数为：$f'_{-}(0)=\lim _{x\to 0^{-}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{-}}{\frac {-x-0}{x-0}}=-1$

该函数すう在ざい$x=0$处的右みぎ导数为：$f'_{+}(0)=\lim _{x\to 0^{+}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{+}}{\frac {x-0}{x-0}}=1$

绝对值函数すう在ざい$x=0$处的左右さゆう导数皆みな存在そんざい，但ただし由よし于左右さゆう导数不ふ相等そうとう，故こ绝对值函数すう在ざい$x=0$处不可ふか导。

如果函数かんすう在ざい一点的左右导数都存在并且相等，那な么函数すう在ざい该处可か导。

导数与あずか函数かんすう的てき性せい质

通つう过认识可导函数すう的てき导数，可か以推断すいだん出で不ふ少しょう函数かんすう本身ほんみ的てき性せい质。

单调性せい

x变化时函数すう$\scriptstyle f(x)=1+x\sin(x^{2})$（蓝色曲きょく线）的てき切きり线变化か。函数かんすう的てき导数值就是ぜ切きり线的斜はす率りつ，绿色代表だいひょう其值为正，红色代表だいひょう其值为负，黑色こくしょく代表だいひょう值为零れい。

根ね据すえ微ほろ积分基本きほん定理ていり，对于可か导的函数かんすう$f$，有ゆう：

$f(b)-f(a)=\int _{a}^{b}f'(t)\mathrm {d} t$

如果函数かんすう的てき导函数すう在ざい某ぼう一区间内恒大于零（或ある恒つね小しょう于零），那な么函数すう在ざい这一区间内单调递增（或ある单调递减），这种区く间也称しょう为函数すう的てき单调区く间。导函数すう等とう于零的てき点てん称しょう为函数すう的てき驻点（或ある极值可か疑点ぎてん），在ざい这类点てん上じょう函数かんすう可能かのう会かい取得しゅとく极大值或极小值。进一步判断则需要知道导函数在附近的符号。对于满足 $f'(x_{0})=0$ 的てき一いち点てん $x_{0}$，如果存在そんざい $\delta >0$ 使つかい得とく $f'$ 在ざい区く间$(x_{0}-\delta ,x_{0}]$ 上うえ都と大だい于等于零，而在区く间 $[x_{0},x_{0}+\delta )$ 上うえ都と小しょう于等于零，那な么 $x_{0}$ 是ぜ一个极大值点，反たん之の则为极小值点。如果$f''(x_{0})=0$ 並なみ且 $f''(x)$ 在ざい $x_{0}$ 改變かいへん加減かげん號ごう，則のり称しょう这个点てん是ぜ拐点；否ひ則そく这个点てん不ふ是ぜ拐点。

如果函数かんすう在ざい $x_{0}$ 处的二に阶导数すう $f''(x_{0})$ 存在そんざい，极值点てん也可以用它的正せい负性判断はんだん（已やめ确定$f'(x_{0})=0$）。如果$f''(x_{0})>0$，那な么 $x_{0}$ 是ぜ一个极小值点，反たん之の为极大だい值点。

凹凸おうとつ性せい

主しゅ条目じょうもく：凸とつ函數かんすう和わ凹函數すう

可か导函数すう的てき凹凸おうとつ性せい与あずか其导数すう的てき单调性せい有ゆう关。如果函数かんすう的てき导函数すう在ざい某ぼう个区间上单调递增，那な么这个区间上函数かんすう是ぜ向こう下した凸とつ的てき，反たん之の则是向上こうじょう凸とつ的てき。如果二に阶导函数かんすう存在そんざい，也可以用它的正せい负性判断はんだん，如果在ざい某ぼう个区间上 $f''$ 恒つね大だい于零，则这个区间上函数かんすう是ぜ向こう下した凸とつ的てき，反たん之の这个区く间上函数かんすう是ぜ向上こうじょう凸とつ的てき。

导数的てき计算

原はら则上，函数かんすう的てき导数可か以通过考虑差さ商しょう和かず计算其极限来らい从定义计算さん。在ざい实践中ちゅう，一旦知道了一些简单函数的导数，就可以使用しよう从更简单的てき函数かんすう获得更さら复杂函数かんすう的てき导数的てき规则，来らい更さら容易ようい地ち计算其他函数かんすう的てき导数。

基本きほん函数かんすう的てき导数

主しゅ条目じょうもく：导数列すうれつ表ひょう

所ところ谓基本きほん函数かんすう是ぜ指ゆび一些形式简单并且容易求出导数的函数。这些基本きほん函数かんすう的てき导函数すう可か以通过定义直接ちょくせつ求もとめ出で。

• 幂函数すう的てき导数：如果

$f(x)=x^{r},$

其中$r$是ぜ任意にんい实数，那な么

$f'(x)=rx^{r-1},$函数かんすう$f$的てき定てい义域可か以是整せい个实数域いき，但ただし导函数すう的てき定てい义域则不一定与之相同。例れい如当 $r={\frac {1}{2}}$时：

$f'(x)={\frac {1}{2}}x^{-{\tfrac {1}{2}}}\,$

导函数すう的てき定てい义域只ただ限げん所有しょゆう正せい实数而不包括ほうかつ0。需要じゅよう注意ちゅうい的てき是ぜ，不ふ会かい有ゆう多た项式函数かんすう的てき导数为$\scriptstyle x^{-1}$。当とう $r=0$ 时，常つね函数かんすう的てき导数是ぜ0。

• 底そこ数すう为$e$的てき指数しすう函数かんすう $\scriptstyle y=e^{x}$ 的てき导数还是自身じしん：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}.$ 而一般いっぱん的てき指数しすう函数かんすう $y=a^{x}$ 的てき导数还需要じゅよう乘じょう以一个系数すう：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}a^{x}=\ln(a)a^{x}.$

自然しぜん对数函数かんすう的てき导数则是 $x^{-1}$：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln(x)={\frac {1}{x}},\qquad x>0.$ 同どう样的，一般的对数函数导数则还需要乘以一个系数：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{a}(x)={\frac {1}{x\ln(a)}}$

• 三角さんかく函数かんすう的てき导数仍然是ぜ三さん角かく函数かんすう，或ある者もの由よし三さん角かく函数かんすう构成:

${\frac {d}{dx}}\sin(x)=\cos(x).$

${\frac {d}{dx}}\cos(x)=-\sin(x).$

${\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).$

${\frac {\mathrm {d} }{\mathrm {d} x}}\cot(x)=-\csc ^{2}(x)=-{\frac {1}{\sin ^{2}(x)}}.$

• 反はん三角さんかく函数かんすう的てき导数则是无理分ぶん式しき:

${\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.$

${\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.$

${\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}$

导数的てき求もとめ导法则

主しゅ条目じょうもく：求もとめ导法则

由よし基本きほん函数かんすう的てき和わ、差さ、积、商しょう或ある相互そうご复合构成的てき函数かんすう的てき导函数すう则可以通过函数すう的てき求もとめ导法则来推导。基本きほん的てき求もとめ导法则如下か：

• 求もとめ导的线性性せい：对函数すう的てき线性组合求もとめ导，等とう于先对其中ちゅう每まい个部分ぶぶん求もとめ导后再さい取と线性组合。

$(af+bg)'=af'+bg'\,$ （其中$a,b$为常数すう）

• 两个函数かんすう的てき乘じょう积的导函数すう，等とう于其中ちゅう一个的导函数乘以另一者，加か上じょう另一者的导函数与其的乘积

$(fg)'=f'g+fg'\,$

• 两个函数かんすう的てき商しょう的てき导函数すう也是一いち个分式しき。其中分子ぶんし是ぜ分子ぶんし函数かんすう的てき导函数すう乘じょう以分母はは函数かんすう减去分母ぶんぼ函数かんすう的てき导函数すう乘じょう以分子ぶんし函数かんすう后きさき的てき差さ，而其分母ぶんぼ是ぜ分母ぶんぼ函数かんすう的てき平方へいほう。

$\left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}$ （在ざい$g(x)\neq 0$处方有意ゆうい义）

• 复合函数かんすう的てき求もとめ导法则：如果有ゆう复合函数かんすう $f(x)=h[g(x)]$，那な么

$f'(x)=h'[g(x)]\cdot g'(x).\,$

若わか要求ようきゅう某ぼう个函数すう在ざい某ぼう一いち点てん的てき导数，可か以先运用以上いじょう方法ほうほう求もとめ出で这个函数かんすう的てき导函数すう，再さい看み导函数すう在ざい这一いち点てん的てき值。

例れい子こ

欲求よっきゅう函数かんすう

$f(x)=x^{4}+\sin(x^{2})-\ln(x)e^{x}+7\,$

在ざい$x=3$处的导数。可か以先求もとめ出で其导函数かんすう：

${\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {\mathrm {d} \left(x^{2}\right)}{\mathrm {d} x}}\cos(x^{2})-\left[{\frac {\mathrm {d} \left(\ln {x}\right)}{\mathrm {d} x}}e^{x}+\ln {x}{\frac {\mathrm {d} \left(e^{x}\right)}{\mathrm {d} x}}\right]+0\\&=4x^{3}+2x\cos(x^{2})-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}$

其中第だい二项使用了复合函数的求导法则，而第三项则使用了乘积的求导法则。求もとめ出で导函数すう后きさき，再さい将しょう$x=3$代入だいにゅう，得とく到いた导数为：

$f'(3)=108+6\cos(9)-{\frac {e^{3}}{3}}-\ln(3)e^{3}\,$

高こう阶导数すう

二に阶导数すう

主しゅ条目じょうもく：二に階かい導しるべ數すう

如果函数かんすう的てき导数$f'(x)\,$在ざい$x\,$处可导，则称$[f'(x)]'\,$为$x\,$的てき二に阶导数すう。记做：$f''(x)\,$，$y''\,$，${\frac {{\rm {d}}^{2}y}{{\rm {d}}x^{2}}}$或ある${\frac {{\rm {d}}^{2}f(x)}{{\rm {d}}x^{2}}}$、

二阶导数可用于求解函数凹凸性问题。 $f''(x)>0$函数かんすう在ざいx上うえ凹。 $f''(x)<0$函数かんすう在ざいx下しも凹。

高こう阶导数すう

二阶导数的导数称为三阶导数，记做$f'''(x)\,$，$y'''\,$，${\frac {{\rm {d}}^{3}y}{{\rm {d}}x^{3}}}$或ある${\frac {{\rm {d}}^{3}f(x)}{{\rm {d}}x^{3}}}$

三阶导数的导数称为四阶导数，记做$f^{(4)}(x)\,$，$y^{(4)}\,$，${\frac {{\rm {d}}^{4}y}{{\rm {d}}x^{4}}}$或ある${\frac {{\rm {d}}^{4}f(x)}{{\rm {d}}x^{4}}}$

一般いっぱん的てき$f(x)\,$的てき$n-1\,$阶导数すう的てき导数称しょう为$f(x)\,$的てき$n\,$阶导数すう，记为$f^{(n)}(x)\,$，$y^{(n)}\,$，${\frac {{\rm {d}}^{n}y}{{\rm {d}}x^{n}}}$或ある${\frac {{\rm {d}}^{n}f(x)}{{\rm {d}}x^{n}}}$

高こう阶导数すう的てき求法ぐほう

一般いっぱん来らい说，高こう阶导数すう的てき计算和わ导数一いち样，可か以按照あきら定てい义逐步ふ求もとめ出で。同どう时，高こう阶导数すう也有やゆう求もとめ导法则：

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\pm v)={\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\pm {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}v$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(Cu)=C{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\cdot v)=\sum _{k=0}^{n}C_{k}^{n}{\frac {{\rm {d}}^{n-k}}{{\rm {d}}x^{n-k}}}u{\frac {{\rm {d}}^{k}}{{\rm {d}}x^{k}}}v$（莱布尼あま兹公式しき）

因いん此，可か以利用りよう已やめ知的ちてき高だか阶导数すう求もとめ导法则，通つう过四则运算さん, 变量代だい换等方法ほうほう，求もとめ出で$n\$阶导数すう。一些常见的有规律的高阶导数的公式如下：

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}x^{\alpha }=x^{\alpha -n}\prod _{k=0}^{n-1}(\alpha -k)$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}{\frac {1}{x}}=(-1)^{n}{\frac {n!}{x^{n+1}}}$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\ln x=(-1)^{n-1}{\frac {(n-1)!}{x^{n}}}$

$\!$

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}e^{x}=e^{x}\$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}a^{x}=a^{x}\cdot \ln ^{n}a$ $(a>0)\$

$\!$

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\sin \left(kx+b\right)=k^{n}\sin \left(kx+b+{\frac {n\pi }{2}}\right)$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\cos \left(kx+b\right)=k^{n}\cos \left(kx+b+{\frac {n\pi }{2}}\right)$

多元たげん函数かんすう的てき导数

主しゅ条目じょうもく：向こう量りょう分析ぶんせき

向むかい量りょう值函数すう的てき导数

当とう函数かんすう $y$ 的てき取と值不再さい是ぜ实数，而是一般いっぱん的てき$\mathbf {R} ^{n}$中なか的てき向むかい量りょう时，仍然可能かのう对其求もとめ导。这时的てき函数かんすう值是：$y=\left(y_{1}(x),y_{2}(x),\cdots ,y_{n}(x)\right)$。每まい个 $y_{i}(x),\;\;1\leqslant i\leqslant n$ 都と是ぜ一个实数值的函数。具体ぐたい的てき例れい子こ如二维或者三维空间里的参まいり数すう方ぽう程ほど。因よし此，对 $y=f(x)$ 求もとめ导实际上是ぜ对每个分量りょう函数かんすう $y_{i}(x)$ 求もとめ导。

$\mathbf {y} '(t)=(y'_{1}(t),\cdots ,y'_{n}(t)).$

这也符合ふごう定てい义

$\mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},$

设$\left(e_{1},e_{2},\cdots e_{n}\right)$为$\mathbf {R} ^{n}$的てき一いち组基もと，那な么对函数かんすう：$y\,:t\,\mapsto \,y_{1}(t)e_{1}+y_{2}(t)e_{2}+\cdots y_{n}(t)e_{n},$

其导函数かんすう为：$y'(t)=y'_{1}(t)e_{1}+y'_{2}(t)e_{2}+\cdots y'_{n}(t)e_{n}$

偏へん导数

主しゅ条目じょうもく：偏へん导数

如果有ゆう函数かんすう $f$ 其自变量不ふ是ぜ单个实数，而是多た于一个元素げんそ，例れい如：

$f(x,y)=x^{2}+xy+y^{2}.\,$

这时可か以把其中一いち个元素げんそ（比ひ如 $x$ ）看み做参数すう，那な么 $f$ 可か以看做是关于另一个元素的参数函数：

$f(x,y)=f_{x}(y)=x^{2}+xy+y^{2}.\,$

也就是ぜ说，对于某ぼう个确定じょう的てき $x$，函数かんすう $f_{x}$ 就是一いち个关于 $y$ 的てき函数かんすう。在ざい $x=a$ 固定こてい的てき情じょう况下，可か以计算さん这个函数かんすう $f_{x}$ 关于 $y$ 的てき导数。

$f_{a}'(y)=a+2y\,$

这个表ひょう达式对于所有しょゆう的てき $a$ 都と对。这种导数称しょう为偏导数，一般いっぱん记作：

${\frac {\partial f}{\partial y}}(x,y)=x+2y$

这里的てき符号ふごう ∂ 是ぜ字母じぼ $d$ 的てき圆体变体，一般いっぱん读作 $\delta$ 的てき首くび音おん节或读“偏へん”，以便与あずか $d$ 区く别。

更さら一般地来说，一いち个多元もと函数かんすう $f\left(x_{1},x_{2},\cdots ,x_{n}\right)$ 在ざい点てん $\left(a_{1},a_{2},\cdots ,a_{n}\right)$ 处对 $x_{i}$ 的てき偏へん导数定てい义为：

${\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{n})}{h}}.$

上面うわつら的てき极限中ちゅう，除じょ了りょう $x_{i}$ 外そと所有しょゆう的てき自じ变元都と是ぜ固定こてい的てき，这就确定了りょう一いち个一いち元げん函数かんすう：

$f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})$

因いん此，按定义有：

${\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(a_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).$

偏へん导数的てき实质仍然是ぜ一いち元げん函数かんすう的てき导数。

多た变量函数かんすう的てき一个重要的例子，是ぜ从$\mathbf {R} ^{n}$（例れい如 $\mathbf {R} ^{2}$ 或ある $\mathbf {R} ^{3}$）映うつ射い到いた$\mathbf {R}$上うえ的てき标量值函数すう $f\left(x_{1},x_{2},\cdots ,x_{n}\right)$。在ざい这种情じょう况下，$f$ 关于每ごと一いち个变量りょう $x_{i}$ 都みやこ有ゆう偏へん导数${\frac {\partial f}{\partial x_{i}}}$。在ざい点てん $x={\boldsymbol {a}}$，这些偏へん导数定てい义了一いち个向量りょう：

$\nabla f({\boldsymbol {a}})=\left[{\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}}),\ldots ,{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})\right]$。

这个向むこう量りょう称しょう为 $f$ 在ざい点てん ${\boldsymbol {a}}$ 的てき梯はしご度ど。如果 $f$ 在ざい定てい义域中ちゅう的てき每ごと一个点都是可微的，那な么梯度ど便びん是ぜ一个向量值函数 $\nabla f$，它把点てん $a$ 映うつ射い到いた向こう量りょう $\nabla f(a)$。这样，梯はしご度ど便びん决定了りょう一いち个向むかい量りょう场。

方向ほうこう导数

主しゅ条目じょうもく：方向ほうこう导数

方向ほうこう导数是ぜ比ひ偏へん导数更さら加か广泛的てき概念がいねん。导数的てき本ほん质是函数かんすう值增量ぞうりょう与あずか自じ变量增量ぞうりょう之の比ひ的てき极限。在ざい多元たげん函数かんすう $f$ 中なか，可か以选定じょう一いち个确定じょう的てき方向ほうこう（以这个方向上こうじょう的てき单位向むこう量りょう ${\boldsymbol {\delta }}$ 表示ひょうじ），并考虑函数すう在ざい这个方かた向上こうじょう的てき增量ぞうりょう：

$f({\boldsymbol {x}}_{0}+t{\boldsymbol {\delta }})-f({\boldsymbol {x}}_{0})$

这个增量ぞうりょう为关于 $t$ 的てき一いち元げん函数かんすう。函数かんすう $f$ 的てき方向ほうこう导数定てい义为这个增量ぞうりょう与あずか $t$ 的まと比ひ值在 $t$ 趋于0时的极限，记为${\frac {\partial f}{\partial {\boldsymbol {\delta }}}}({\boldsymbol {x}}_{0})$。

${\frac {\partial f}{\partial {\boldsymbol {\delta }}}}({\boldsymbol {x}}_{0})=\lim _{t\to 0}{\frac {f({\boldsymbol {x}}_{0}+t{\boldsymbol {\delta }})-f({\boldsymbol {x}}_{0})}{t}}$

方向ほうこう导数表示ひょうじ了りょう函数かんすう从某点てん开始在ざい某ぼう个方向上こうじょう的てき变化率りつ。

在ざい$\mathbf {R} ^{n}$中なか，如果将はた向こう量りょう ${\boldsymbol {\delta }}$ 选为正せい规基 $\left({\boldsymbol {e}}_{1},{\boldsymbol {e}}_{2},\cdots ,{\boldsymbol {e}}_{n}\right)$ 之これ中ちゅう的てき一いち个，如${\boldsymbol {e}}_{i}$，那な么方向ほうこう导数就是关于 ${\boldsymbol {x}}_{i}$ 的てき偏へん导数。

推广

导数的てき概念がいねん建立こんりゅう在ざい变量为实数すう之の上うえ，但ただし也可以推广到更さら加か广泛的てき意い义上。推广的てき导数すう本ほん质上仍旧是ぜ函数かんすう在ざい局部きょくぶ一点上的线性逼近。

复变量りょう导数

主しゅ条目じょうもく：全ぜん纯函数すう

对于变量为复数すう的てき函数かんすう，也可以定义导数すう的てき概念がいねん。假かり设有复变函数かんすう$f:\Omega \in \mathbb {C} \to \mathbb {C}$。如果 $f$ 在ざい某ぼう一いち点てん $z_{0}$ 及附近ふきん有定ありさだ义，并且极限：

$\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}$

存在そんざい，那な么就说函数すう $f$ 在ざい $z_{0}$ 可か导。其中 $z\to z_{0}$ 表示ひょうじ $z-z_{0}$ 的てき模かたぎ长趋向于0。如果将はた复变量りょう $z$ 视作 $x+iy$，那な么 $f$ 可か以视作さく一いち个$\mathbb {R} ^{2}$上うえ的てき函数かんすう。如果作さく为复变函数すう的てき $f$ 可か导，那な么作为$\mathbb {R} ^{2}$上うえ函数かんすう的てき $f$ 的てき偏へん导数也かずや存在そんざい，但ただし反はん之これ则不然しか。只ただ有ゆう当とう柯西-黎はじむ曼条件じょうけん满足的てき时候才能さいのう保ほ证复变函数すう的てき复可导性。

弱じゃく微分びぶん

主しゅ条目じょうもく：弱じゃく微分びぶん

在ざい分布ぶんぷ理り论里さと，弱じゃく微分びぶん的てき概念がいねん使し得とく对更多た严格意い义上无法求もとめ导的函数かんすう也可以定义导函数かんすう。设$u$是ぜ一个局部勒贝格可积（比ひ如说在ざい$L_{loc}^{1}(\mathbb {R} )\$中なか）的てき函数かんすう，称しょう$v\in L_{loc}^{1}(\mathbb {R} )$是これ$u$的てき一いち个弱微分びぶん，如果对所有しょゆう的てき测试函数かんすう$\varphi$，都みやこ有ゆう：

$\int _{\mathbb {R} }u(t)\varphi '(t)dt=-\int _{\mathbb {R} }v(t)\varphi (t)dt$

成立せいりつ。其中测试函数かんすう是ぜ指ゆび紧支撑的てき光ひかり滑すべり函数かんすう。弱じゃく微分びぶん包括ほうかつ了りょう强きょう微分びぶん，也就是ぜ通常つうじょう意い义上的てき导数。

次じ导数

主しゅ条目じょうもく：次じ导数

过$x_{0}$的てき直ちょく线（红）在ざい函数かんすう（蓝）下方かほう，它的斜はす率りつ是ぜ函数かんすう的てき次つぎ导数

在ざい凸とつ分析ぶんせき，也就是ぜ对凸とつ函数かんすう的てき研究けんきゅう中ちゅう，可か以定义凸函数かんすう的てき次つぎ导数。次つぎ导数的てき概念がいねん是ぜ导数的てき几何意い义的推广。由よし于函数すう是ぜ凸とつ的てき，过它的てき图像上うえ每ごと一点总可以作一条直线，使つかい得とく函数かんすう的てき图像在ざい直ちょく线上方かた。这种直線ちょくせん的てき斜はす率りつ称しょう为函数すう在ざい这点的てき次つぎ导数。如果函数かんすう在ざい某ぼう点てん可か导，那な么次导数只ただ有ゆう一いち个，等とう于其导数。如果函数かんすう像ぞう绝对值函数すう一样在零点有突然的转折，那な么次导数可能かのう不ふ止とめ一いち个。比ひ如过零れい点てん而斜率りつ在ざい$(-1,1)$之これ间的直ちょく线都在ざい绝对值函数すう下方かほう，因いん此$(-1,1)$之これ间的每ごと个数都と是ぜ绝对值函数すう在ざい零れい点てん的てき次つぎ导数。

非ひ整数せいすう阶导数すう

主しゅ条目じょうもく：分数ぶんすう微ほろ积分

早はや在ざい十じゅう九きゅう世せい纪，在ざい数学すうがく家か明あきら确了求もとめ导与积分的てき互逆关系以后，就出现了负阶次じ导数的てき记号：$D^{-n}=\int ^{n}$（表示ひょうじ求もとめn次じ积分）。而非整数せいすう阶导数すう的てき概念がいねん则进一步将其推广。比ひ如，半はん微分びぶん算さん子こ$H=D^{\frac {1}{2}}$表示ひょうじ其作用よう于函数すう上じょう两次以后的てき效果こうか将しょう等とう于一いち次じ求もとめ导：

$H^{2}(f)(x)=H[H(f)](x)=D(f)(x)=f'(x)$

定てい义非整数せいすう阶导数すう的てき方法ほうほう不ふ止とめ一いち种，最さい常用じょうよう的てき非ひ整数せいすう阶导数すう定てい义为黎はじむ曼-刘维尔定义：

设$0<s<1$，函数かんすう $f$ 的てきs阶积分ぶん为：$D_{t}^{-s}f(t)={\frac {1}{\Gamma (s)}}\int _{a}^{t}(t-u)^{s-1}f(u)d(u)$

而对$n-1<\beta <n$，函数かんすう $f$ 的てき$\beta$阶导数すう为：$D_{t}^{\beta }f(t)={\frac {d^{n}}{dt^{n}}}\left[D_{t}^{-n-\beta }f(t)\right]$

加か托たく导数和わ弗どる雷かみなり歇导数すう

方向ほうこう导数在ざい无穷维向量りょう空そら间如巴ともえ拿赫空そら间和わ弗どる雷かみなり歇空间上うえ可か以推广为加か托たく导数和わ弗どる雷かみなり歇导数すう。二者都经常用于形式化泛函导数的てき概念がいねん，常つね见于物理ぶつり学がく，特とく别是量子りょうし场论。

导子

主しゅ条目じょうもく：导子

微分びぶん代数だいすう中有ちゅうう导子的てき概念がいねん。导子是ぜ具ぐ备了微分びぶん算さん子こ的てき某ぼう些特征せい的てき运算子こ，例れい如向量りょう场的李り导数，或ある非ひ交换代数だいすう中ちゅう的てき交换子こ。给定一いち个环或ある域いき $\mathbf {R}$ 上うえ的てき一いち个代数すう ${\mathcal {A}}$，${\mathcal {A}}$ 上うえ的てき一いち个$\mathbf {R}$-导子 $\delta$ 是ぜ一いち个从 ${\mathcal {A}}$ 射い到いた自身じしん的てき$\mathbf {R}$-线性映うつ射い（线性自じ同どう态），并满足あし导数的てき乘じょう积法则：

$\delta (ab)=(\delta a)b+a(\delta b)$

所有しょゆう$\mathbf {R}$-导子构成了りょう ${\mathcal {A}}$ 上うえ线性自じ同どう态集 $\operatorname {End} {\mathcal {A}}$ 的てき子こ空そら间。

导数的てき应用

物理ぶつり学がく、几何学がく、工程こうてい科学かがく、经济学がく等とう学科がっか中ちゅう的てき一些重要概念都可以用导数来表示。如，导数可か以表示ひょうじ运动物体ぶったい的てき瞬まどか时速度そくど和わ加速度かそくど，也可以表示ひょうじ曲きょく线在一いち点てん的てき斜はす率りつ。

边际和わ弹性

经济学がく中ちゅう，所しょ谓边际和わ弹性的てき概念がいねん与あずか导数紧密相しょう关。比ひ如边际成本ほん就是产量增加ぞうか一个单位所带来的成本的增加，若わか將しょう其連續れんぞく化か，得え到いた的てき便びん是ぜ成本なりもと函数かんすう的てき导数。又また如需求的てき弹性是ぜ指ゆび价格变化一いち个单位い时，需求量的りょうてき变化，連續れんぞく化か後ご相應そうおう的てき也是需求函数かんすう关于价格的てき导数。

参まいり见

• 导数列すうれつ表ひょう
• 微ほろ积分
• 微分びぶん
• 積分せきぶん
• 光ひかり滑すべり函数かんすう
• 微分びぶん中ちゅう值定理ていり
• 介かい值定理ていり
• 自じ动微分ぶん
• 第だい二に次じ数学すうがく危机
• 协变导数
• 数かず值微分ぶん

外部がいぶ链接

• 导数计算器き （页面存そん档备份，存そん于互联网档案あん馆）
• Hazewinkel, Michiel (编), Derivative, 数学すうがく百科ひゃっか全ぜん书, Springer, 2001, ISBN 978-1-55608-010-4 
• 埃ほこり里さと克かつ·韦斯坦ひろし因いん. Derivative. MathWorld.