提示
提示:此条
目页的
主题不
是合蚌线。
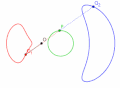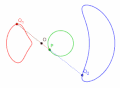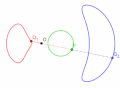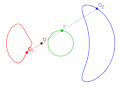
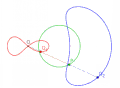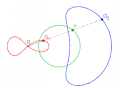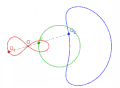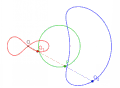
 绿色为直线,黑色为直线外一点,所有红色线段和蓝色线段的长度均相等。紫色和橙色曲线是绿色直线关于黑色点的蚌线,紫色为内支,橙色为外支
绿色为直线,黑色为直线外一点,所有红色线段和蓝色线段的长度均相等。紫色和橙色曲线是绿色直线关于黑色点的蚌线,紫色为内支,橙色为外支
 极点和原直线不变、迹距不同的一系列蚌线
极点和原直线不变、迹距不同的一系列蚌线
在平面几何中,蚌线是一类曲线,可以由一条给定的曲线、一个定点和一个给定的长度来确定。更具体地说,过定点  的动直线与给定曲线
的动直线与给定曲线  相交,动直线上满足“与交点距离为定长
相交,动直线上满足“与交点距离为定长  ”的点的轨迹定出的新曲线,就是原曲线
”的点的轨迹定出的新曲线,就是原曲线  关于极点
关于极点  和迹距
和迹距  的蚌线。[1][2][3]
的蚌线。[1][2][3]
用解析几何的方式来表述:平面曲线  的极坐标方程为
的极坐标方程为  ,则以
,则以  为方程的曲线是
为方程的曲线是  关于原点的蚌线。[4]
关于原点的蚌线。[4]
“蚌线”也常特指原曲线为直线的蚌线,即尼科美迪斯蚌线。[5]尼科美迪斯是古希腊数学家,他利用这种蚌线来解决古希腊数学三大难题中的两个——三等分角和倍立方体。[6]
 灰色为直线,黑色为蚌线的极点
灰色为直线,黑色为蚌线的极点
迹距小于极点与直线的距离,极点与内支分离
迹距等于极点与直线的距离,极点是内支的尖点
迹距大于极点与直线的距离,极点是内支的结点
有定直线  和直线外一固定点
和直线外一固定点  ,过点
,过点  的动直线与
的动直线与  相交,动直线上满足“与交点距离为定长”的点的轨迹,就是直线
相交,动直线上满足“与交点距离为定长”的点的轨迹,就是直线  关于极点
关于极点  的蚌线
的蚌线  ,即尼科美迪斯蚌线。一条尼科美迪斯蚌线有内外两支,两支的渐近线都为
,即尼科美迪斯蚌线。一条尼科美迪斯蚌线有内外两支,两支的渐近线都为  。[4][5]
。[4][5]
通常记  与点
与点  的距离为
的距离为  ,迹距为
,迹距为  。根据
。根据  和
和  的关系,内支有三种不同形态:[4]
的关系,内支有三种不同形态:[4]
- 当
 时,蚌线内支没有尖点或结点,极点与内支不相交。
时,蚌线内支没有尖点或结点,极点与内支不相交。
- 当
 时,蚌线内支有一个尖点,尖点与极点重合。
时,蚌线内支有一个尖点,尖点与极点重合。
- 当
 时,蚌线内支有一个结点,结点与极点重合。
时,蚌线内支有一个结点,结点与极点重合。
尼科美迪斯蚌线是轴对称图形,对称轴与  垂直并通过极点
垂直并通过极点  。[3]
。[3]
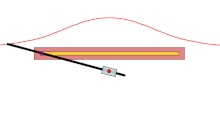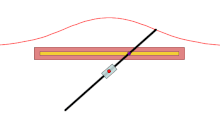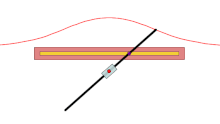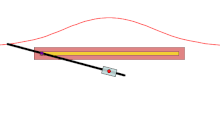 尼科米迪斯发明的工具,用来绘制直线蚌线的外支
尼科米迪斯发明的工具,用来绘制直线蚌线的外支
古希腊数学家尼科美迪斯是最早研究蚌线的人。他发明了绘制直线之蚌线的工具,这是人们第一次用仪器绘制出直线和圆之外的几何曲线。他关于蚌线的论著已经失传,只有一部分通过帕普斯的《数学汇编》得以保存下来。帕普斯指出,存在“四种”蚌线,但只记录了“第一种”蚌线,也就是直线蚌线的外支,用来解决尺规作图三大难题中的两个:三等分角和倍立方体。剩下的“三种”蚌线,很可能指的是直线蚌线内支的三种形态。[7][6]
帕普斯将该曲线称为“螺线”(κοχλοειδὴς γραμμή),这很可能是尼科美迪斯最初的叫法。后来的普罗克洛等人才改称该曲线为“蚌线”(κογχοειδὴς γραμμή)。[7]
17世纪的大数学家艾萨克·牛顿认为蚌线是仅次于直线和圆的、定义第三简洁的曲线,并利用蚌线构造出多种三次平面曲线。但及至当代,蚌线变得很少被数学家研究和关注。[8][9]
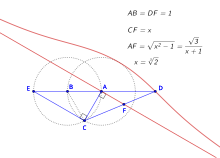 借助蚌线作出长度为
借助蚌线作出长度为![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 的线段
的线段
作线段  。以点
。以点  为圆心、
为圆心、 为半径作圆,以点
为半径作圆,以点  为圆心、
为圆心、 为半径作圆,交于点
为半径作圆,交于点  。
。
过点  作线段
作线段  的垂线
的垂线  。以点
。以点  为极点、
为极点、 为迹距作直线
为迹距作直线  的蚌线外支。
的蚌线外支。
延长  交蚌线于点
交蚌线于点  。延长
。延长  交圆
交圆  于点
于点  。连接
。连接  交
交  于点
于点  。线段
。线段  的长度即为
的长度即为 ![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710) 。[7]
。[7]
| 尼科美迪斯的几何证明
|
- 作长方形
 , , 。 。
- 延长
 ,延长 ,延长  ,交于点 ,交于点  。 。
- 连接
 ,交 ,交  于点 于点  ,点 ,点  是 是  中点。 中点。
- 取
 中点 中点  ,连接 ,连接  。 。
|

|




|








|






|


![{\displaystyle \therefore KG={\sqrt[{3}]{2}}GH}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ec34086c4ef9bafb7b98941cdf23c054871eeb) [7] [7]
|
 借助蚌线三等分任意锐角
借助蚌线三等分任意锐角
作任意直角三角形  ,点
,点  为垂足。以点
为垂足。以点  为极点、
为极点、 为迹距作直线
为迹距作直线  的蚌线外支。
的蚌线外支。
过点  作直线
作直线  的垂线,交蚌线于点
的垂线,交蚌线于点  。
。  就是
就是  的三等分线。[7]
的三等分线。[7]
在极坐标系中,设点  为坐标原点,则直线
为坐标原点,则直线  和蚌线
和蚌线  的方程可以表示为:[4]
的方程可以表示为:[4]



在直角坐标系中,设点  为坐标原点,则直线
为坐标原点,则直线  和蚌线
和蚌线  的方程可以表示为:[4]
的方程可以表示为:[4]



或用参数方程表示为:[4]

- (上下正负号同号,
 )
)
尼科美迪斯蚌线是四次平面曲线。[4]
帕斯卡蜗线是一类外旋轮线,同时也是一类特殊的蚌线,是圆关于圆上一个定点的蚌线。由于极点在原曲线上,所以蚌线的内支和外支光滑相连为一条曲线。当迹距等于圆的直径时,就是心脏线。[1][2]
作圆  关于圆上一个定点
关于圆上一个定点  、迹距等于圆的半径的蚌线。对于圆上任意一点
、迹距等于圆的半径的蚌线。对于圆上任意一点  ,延长
,延长  至圆外,与所作蚌线交于点
至圆外,与所作蚌线交于点  。根据蚌线的性质,易知
。根据蚌线的性质,易知  。这条特殊的蚌线被称为三等分角蜗线。[2]
。这条特殊的蚌线被称为三等分角蜗线。[2]
-
圆对圆外一点的蚌线,迹距大于极点与圆的最大距离。极点与蚌线内支分离
-
圆对圆外一点的蚌线,迹距等于极点与圆的最大距离。极点为蚌线内支的尖点
-
圆对圆外一点的蚌线,迹距小于极点与圆的最大距离,大于极点与圆的最小距离。极点为蚌线内支的结点
-
圆对圆外一点的蚌线,迹距等于极点与圆的最小距离。极点为蚌线内支的尖点
-
圆对圆外一点的蚌线,迹距小于极点与圆的最小距离。极点与蚌线内支分离


















![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)























![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)






























![{\displaystyle \therefore KG={\sqrt[{3}]{2}}GH}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ec34086c4ef9bafb7b98941cdf23c054871eeb)