幾何 きか 學 がく 粵拼 :gei2 ho4 hok6 英文 えいぶん geometry ;古希 こき γεωμετρία ,geometria )係 がかり 數學 すうがく 一 いち 個 こ 子 こ 領域 りょういき 專門 せんもん 思考 しこう 有 ゆう 關 せき 形狀 けいじょう 物體 ぶったい 相對 そうたい 位置 いち 空間 くうかん 性 せい 等 とう 課題 かだい 幾何 きか 學理 がくり 論 ろん 點 てん 直線 ちょくせん 平面 へいめん 角 かく 維度 等 とう 概念 がいねん 為 ため 基礎 きそ 會 かい 用 よう 數學 すうがく 證明 しょうめい 法 ほう 證明 しょうめい 概念 がいねん 定理 ていり 靠 もたれ 增進 ぞうしん 人類 じんるい 對 たい 概念 がいねん 同 どう 埋 うめ 相應 そうおう 現實 げんじつ 世界 せかい 物體 ぶったい 理解 りかい [1] [2]
幾何 きか 學 がく 歷史 れきし 悠久 ゆうきゅう 公 おおやけ 元 もと 前 まえ 古希 こき 等 ひとし 多 た 個 こ 遠 とお 古 ふる 文明 ぶんめい 都 みやこ 有 ゆう 獨立 どくりつ 建立 こんりゅう 幾何 きか 學 がく 方法 ほうほう 長 なが 度 たび 面積 めんせき 同 どう 容量 ようりょう 等 とう 概念 がいねん 用 よう 設計 せっけい 建築 けんちく 等 とう 種 しゅ 用途 ようと [1] [3] 形式 けいしき 化 か 何 なん 學 がく 源 げん 古希 こき 元 もと 前 まえ 世紀 せいき 古希 こき 數學 すうがく 家 か 歐 おう 幾里 いくさと 得 とく 本名 ほんみょう 著 ちょ 幾何 きか 原本 げんぽん 當 とう 中 ちゅう 用 よう 公理 こうり 化 か 法 ほう 證明 しょうめい 條 じょう 幾何 きか 學 がく 上 じょう 定理 ていり 為 ため 後世 こうせい 何 なん 學 がく 研究 けんきゅう 一 いち 個 こ 重要 じゅうよう 根基 こんき [4] 中 ちゅう 世紀 せいき 至 いたり 世紀 せいき 同 どう 埋 うめ 打 だ 後 ご 學 がく 家 か 亦 また [5] 去 さ 到 いた 現時 げんじ 廿 にじゅう 一 いち 世紀 せいき 初 はつ 幾何 きか 學都 がくと 係 がかり 一 いち 個 こ 活躍 かつやく 研究 けんきゅう 領域 りょういき
喺廿一 いち 世紀 せいき 初 はつ 幾何 きか 學 がく 知識 ちしき 相當 そうとう 有 ゆう 影響 えいきょう 力 りょく [6] 多 おお 科學 かがく 同 どう 工程 こうてい 學 がく 領域 りょういき 上 うえ 都 と 相當 そうとう 有用 ゆうよう 例 れい 古典 こてん 力學 りきがく 分析 ぶんせき 物體 ぶったい 移動 いどう 成 なり 日 び 都會 とかい 用 よう 到 いた 距離 きょり 同 どう 速 はや 率 りつ 等 とう 建 たて 基 はじめ 於幾 おき 何 なに 學 がく 概念 がいねん [7] 電腦 でんのう 圖像 ずぞう 用 よう 電腦 でんのう 整 せい 圖像 ずぞう 一部 いちぶ 電腦 でんのう 整 せい 3D 模型 もけい 嗰時要 よう 運算 うんざん 中途 ちゅうと 用 よう 到 いた 個 こ 模型 もけい 邊 べ 有 ゆう 幾 いく 長 ちょう 同 どう 個 こ 模型 もけい 角 すみ 有 ゆう 幾 いく 大 だい 資 し [8] 建築 けんちく 學 がく 研究 けんきゅう 建築 けんちく 物 ぶつ 設計 せっけい 會 かい 對 たい 建築 けんちく 物 ぶつ 作出 さくしゅつ 幾何 きか 分析 ぶんせき 建築 けんちく 物 ぶつ 部位 ぶい 角度 かくど 同 どう 長 ちょう 度會 わたらい 影響 えいきょう 棟 とう 建築 けんちく 物 ぶつ [9]
平面 へいめん 上面 うわつら 每 ごと 粒 つぶ 點 てん 都 と 可 か 像 ぞう 成 なり 塊 かたまり 平面 へいめん 集 しゅう 入 いれ 面 めん 一 いち 個 こ 元素 げんそ 幾何 きか 學 がく 係 がかり 研究 けんきゅう 空間 くうかん 數學 すうがく 子 こ 領域 りょういき 空間 くうかん 概念 がいねん 要點 ようてん 定義 ていぎ 係 がかり 不 ふ 過 か 基本 きほん 歐 おう 幾里 いくさと 得 とく 幾何 きか 上 じょう 空間 くうかん 可 か 點 てん 直線 ちょくせん 同 どう 埋 うめ 平面 へいめん 等 とう 概念 がいねん 想像 そうぞう
點 てん 係 かかり 幾何 きか 學 がく 上 じょう 一 いち 個 こ 原始 げんし
簡化噉講,點 てん 可 か 定義 ていぎ 間 あいだ 裡 うら 面 めん 有 ゆう 確 かく 切 きり 位置 いち 用 よう 空間 くうかん 長 なが 度 たび 同 どう 闊度 [註 1]
技術 ぎじゅつ 性 せい 講 こう 現代 げんだい 數學 すうがく 有 ゆう 集合 しゅうごう 論 ろん 理論 りろん 框 かまち 架 か 下 か 點 てん 通常 つうじょう 定義 ていぎ 一 いち 個 こ 集 しゅう 空間 くうかん 入 いれ 面 めん 中 ちゅう 一 いち 件 けん 元素 げんそ 例 れい 講 こう 一塊 ひとかたまり 平面 へいめん 上面 うわつら 一 いち 點 てん 首 しゅ 先 さき 定義 ていぎ 塊 かたまり 平面 へいめん 係 がかり [10]
R
2
=
{
(
a
,
b
)
:
a
,
b
∈
R
}
{\displaystyle \mathbb {R} ^{2}=\{(a,b):a,b\in \mathbb {R} \}}
塊 かたまり 平面 へいめん 上 じょう 一 いち 點 てん
p
{\displaystyle p}
R
2
{\displaystyle \mathbb {R} ^{2}}
入 いれ 面 めん 元素 げんそ 用 よう 日常 にちじょう 用語 ようご 講 こう 即 そく 係 がかり
p
{\displaystyle p}
可 か
(
a
,
b
)
{\displaystyle (a,b)}
當 とう 中 なか
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
都 と 係 がかり 實數 じっすう
R
{\displaystyle \mathbb {R} }
一 いち 提 ひさげ 點 てん 原則 げんそく 上 うえ 係 がかり 一 いち 個 こ 抽象 ちゅうしょう 化 か 概念 がいねん 淨 きよし 係 がかり 存在 そんざい 想像 そうぞう 之 これ 中 ちゅう 理論 りろん 上 じょう 係 がかり 度 ど 同 どう 好 こう 似 に 下圖 したず 經 けい 已 やめ 有 ゆう 返 かえし 下長 しもなが 度 ど 同 どう 所以 ゆえん 人 じん 先 さき 可 か 肉眼 にくがん 到 いた 嚴格 げんかく 係 がかり 一 いち 點 てん 頂 いただき 只 ただ 可 か 係 がかり 表示 ひょうじ 一 いち 點 てん 符號 ふごう [11]
點 てん 係 がかり 幾何 きか 學 がく 最 さい 根基 こんき 頭 あたま 有 ゆう 概念 がいねん 得 とく 定義 ていぎ 同 どう 第 だい 要 よう 何 なん 學 がく 概念 がいねん 同 どう 例 れい 是 ぜ 但 ただし 兩 りょう 點 てん 之 の 間 あいだ 都 と 可 か 條 じょう 獨 どく 一 いち 無 む 二 に 公理 こうり [註 2] [11]
直線 ちょくせん 係 かかり 幾何 きか 學 がく 想像 そうぞう 中 ちゅう 一 いち 種 しゅ 闊度 、有 ゆう 長 なが 度 たび 當 とう 中 ちゅう 直 ただし 係 がかり 指 ゆび 上面 うわつら 點 てん 均 ひとし 分 ぶん 線 せん
攞住點 てん 概念 がいねん 想像 そうぞう 但 ただし 兩 りょう 點 てん
A
{\displaystyle A}
同 どう
B
{\displaystyle B}
A
{\displaystyle A}
同 どう
B
{\displaystyle B}
之 これ 間 あいだ 有 ゆう 無限 むげん 粒 つぶ 點 てん 點 てん 之 の 間 あいだ 每 ごと 對 たい 點 てん 之 の 間 あいだ 離 はなれ 都 と 係 がかり 恆 つね 定 てい
=
0
{\displaystyle =0}
用 よう 集合 しゅうごう 論 ろん 角度 かくど 集 しゅう 精確 せいかく 代 だい 幾何 きか 學 がく 入 いれ 面 めん 直線 ちょくせん 通常 つうじょう 定義 ていぎ 線 せん 性 せい 空間 くうかん 入 いれ 面 めん 有 ゆう 某 ぼう 種 しゅ 線 せん 性 せい 關係 かんけい 點 てん 集 しゅう 是 ぜ 但 ただし 一 いち 粒 つぶ 點 てん
p
{\displaystyle p}
同 どう 一 いち 條 じょう 線 せん
ℓ
{\displaystyle \ell }
p
{\displaystyle p}
ℓ
{\displaystyle \ell }
上面 うわつら 或 ある 者 もの
p
{\displaystyle p}
ℓ
{\displaystyle \ell }
上面 うわつら 都會 とかい 係 がかり 有意義 ゆういぎ 子 こ 句 く 係 がかり 真 しん 一 いち 係 がかり 假 かり 平面 へいめん 入 いれ 面 めん 線 せん 有 ゆう 個性 こせい 質 しつ 是 ぜ 但 ただし 點 てん 點 てん 都 と 可 か 一 いち 條 じょう 直線 ちょくせん 連接 れんせつ 歐 おう 幾里 いくさと 得 とく 幾何 きか 一 いち 公理 こうり 所有 しょゆう 能 のう 連接 れんせつ 兩 りょう 點 てん 之 の 中 ちゅう 直線 ちょくせん 係 がかり 長 なが 度 たび 最短 さいたん 好 こう 似 に 下圖 したず 係 がかり 一 いち 條 じょう 線 せん 下圖 したず 條 じょう 線 せん 實質 じっしつ 上 じょう 有 ゆう 會 かい 用 よう 肉眼 にくがん 到 いた 所以 ゆえん 只 ただ 係 がかり [12]
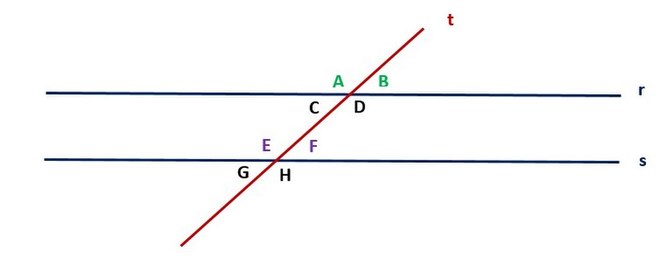
喺歐 おう 幾里 いくさと 得 とく 幾何 きか 入 いれ 面 めん 兩 りょう 條 じょう 直線 ちょくせん 之 の 間 あいだ 可 か 交點 こうてん [e 1] 又 また 可 か 平行 へいこう [e 2] 關係 かんけい 話 ばなし 兩 りょう 條 じょう 線 せん 係 がかり 平行 へいこう 意思 いし 係 がかり 話 ばなし 無論 むろん 將 はた 線 せん 延長 えんちょう 幾多 いくた 都 みやこ 好 よしみ 兩 りょう 條 じょう 線 せん 都 と 有 ゆう 交點 こうてん [13] 好 こう 似 に 下圖 したず 下圖 したず 有 ゆう 三 さん 條 じょう 線 せん
t
{\displaystyle t}
r
{\displaystyle r}
同 どう
s
{\displaystyle s}
當 とう 中 なか
t
{\displaystyle t}
同 どう
r
{\displaystyle r}
頂點 ちょうてん 相 あい
t
{\displaystyle t}
同 どう
s
{\displaystyle s}
都 と 係 がかり 頂點 ちょうてん 相 あい
r
{\displaystyle r}
同 どう
s
{\displaystyle s}
平行 へいこう
直線 ちょくせん 仲 なか 可 か 埋 うめ 曲線 きょくせん 概念 がいねん 曲線 きょくせん 係 がかり 一 いち 種 しゅ 幾何 きか 物體 ぶったい 同 どう 直線 ちょくせん 一 いち 樣 よう 曲線 きょくせん 可 か 像 ぞう 成 なり 由 ゆかり 兩 りょう 點 てん 之 の 間 あいだ 組成 そせい 不 ふ 過 か 曲線 きょくせん 可能 かのう 係 がかり 好 こう 似 に 下圖 したず 技術 ぎじゅつ 性 せい 講 こう 曲線 きょくせん 可 か 像 ぞう 成 なり 直線 ちょくせん 廣義 こうぎ 化 か 線 せん 可 か 所有 しょゆう 由 ゆかり 兩 りょう 點 てん 之 の 間 あいだ 組成 そせい 線 せん 係 がかり 線 せん 一 いち 種 しゅ 特 とく 指 ゆび 上面 うわつら 均 ひとし 分 ぶん 線 せん [14]
喺歐幾里 いくさと 得 とく 幾何 きか 裏面 りめん 一塊 ひとかたまり 平面 へいめん 係 かかり 一塊 ひとかたまり 2D 而且冇曲 きょく 率 りつ [註 3] 何 なん 物體 ぶったい 有 ゆう 長 なが 度 たび 同 どう 闊度 但 ただし 高度 こうど 最少 さいしょう 理論 りろん 上 じょう 可 か 住 じゅう 任 にん 何 なん 方向 ほうこう 無限 むげん 延伸 えんしん 用 よう 最 さい 常用 じょうよう 坐 すわ 標 しるべ 系統 けいとう 平面 へいめん 同 どう 直線 ちょくせん 別 べつ 可 か 像 ぞう 成 なり 要用 ようよう 幾多 いくた 個數 こすう 先 さき 可 か 述 じゅつ 一 いち 點 てん 位置 いち 維度 同 どう 坐 すわ 標 しるべ 等 とう 概念 がいねん [15]
如果要 よう 淨 きよし 係 がかり 要用 ようよう 一 いち 個 こ 數 すう 例 れい
(
x
)
{\displaystyle (x)}
所以 ゆえん 係 がかり 一 いち 1D );
而如果 はて 要 よう 用 よう 兩個 りゃんこ 數 すう 至 いたり 得 え 例 れい
(
x
,
y
)
{\displaystyle (x,y)}
所以 ゆえん 係 がかり 二 に 2D ); 下圖 したず 係 がかり 成 なり 平行 へいこう 三 さん 塊 かたまり 平面 へいめん 想像 そうぞう 即 そく 係 がかり 無限 むげん
歐 おう 幾里 いくさと 得 とく 研究 けんきゅう 何 なん 好 こう 大部 たいぶ 係 がかり 面 めん 入 いれ 面 めん 發生 はっせい 何 なに 即 そく 係 がかり 所謂 いわゆる 平面 へいめん 幾何 きか 包括 ほうかつ 面 めん 上面 うわつら 三角形 さんかっけい 圓形 えんけい 平行 へいこう 線 せん 同 どう 角度 かくど 根據 こんきょ 研究 けんきゅう 平面 へいめん 有 ゆう 好 こう 多 た 特別 とくべつ 性質 せいしつ [16] [17]
是 ぜ 但 ただし 塊 かたまり 面 めん 一 いち 係 がかり 彼此 ひし 成 なり 平行 へいこう 相 あい 是 ぜ 但 ただし 一塊 ひとかたまり 平面 へいめん 同 どう 一 いち 條 じょう 線 せん 條 じょう 線 せん 再 さい 可能 かのう 平面 へいめん 上面 うわつら 如果有 ゆう 兩 りょう 條 じょう 兩 りょう 條 じょう 都 と 係 がかり 同 どう 一塊 ひとかたまり 平面 へいめん 成 なり 垂直 すいちょく 講 こう 成 なり 角 かく 條 じょう 線 せん 實 み 係 がかり 平行 へいこう
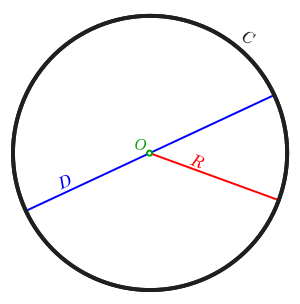
如果有 ゆう 兩 りょう 塊 かたまり 平面 ひらおもて 都 と 同 どう 某 ぼう 條 じょう 線 せん 成 なり 垂直 すいちょく 塊 かたまり 平面 へいめん 實 み 係 がかり 成 なり 平行 へいこう 圓形 えんけい 係 かかり 一 いち 種 しゅ 2D 嘅形狀 けいじょう 用 もちい 坐 すわ 標 しるべ
(
x
,
y
)
{\displaystyle (x,y)}
都會 とかい 滿足 まんぞく 以下 いか 條 じょう 式 しき
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
當 とう 中 なか
(
a
,
b
)
{\displaystyle (a,b)}
係 かかり 個 こ 圓心 えんしん 標 しるべ
r
{\displaystyle r}
係 かかり 個 こ 圓形 えんけい 半徑 はんけい 有 ゆう 幾 いく 長 ちょう 一去到 2D,就可以諗埋 うめ 角 かく 概念 がいねん 是 ぜ 但 ただし 一 いち 點 てん 例 れい 圖 ず
A
{\displaystyle A}
由 ゆかり 向 こう 住 じゅう 兩個 りゃんこ 方向 ほうこう 例 れい 圖 ず
C
1
{\displaystyle C_{1}}
同 どう
C
3
{\displaystyle C_{3}}
各 かく 射 い 兩 りょう 條 じょう 射 い 線 せん 之 の 間 あいだ 形成 けいせい 一 いち 隻 せき 角 かく 下圖 したず
α あるふぁ
2
{\displaystyle \alpha _{2}}
角度 かくど 反映 はんえい 隻 せき 角 かく 有 ゆう 幾 いく 大 だい 際 ぎわ 何 なん 分析 ぶんせき 上 じょう 一 いち 隻 せき 角通 かくつう 常會 じょうかい 用 よう
∠
{\displaystyle \angle }
號 ごう 表示 ひょうじ 下圖 したず
α あるふぁ
2
{\displaystyle \alpha _{2}}
會 かい 寫 うつし
∠
C
1
A
C
3
{\displaystyle \angle C_{1}AC_{3}}
樣 さま 會 かい 用 よう 符號 ふごう 表示 ひょうじ 細 ほそ
∠
A
B
C
=
90
{\displaystyle \angle ABC=90}
表示 ひょうじ
∠
A
B
C
{\displaystyle \angle ABC}
角 かく 係 がかり 類推 るいすい [18]
有 ゆう 點 てん 直線 ちょくせん 曲線 きょくせん 平面 へいめん 同 どう 角 かく 基本 きほん 概念 がいねん 研究 けんきゅう 者 しゃ 現實 げんじつ 世界 せかい 間 あいだ 基本 きほん 分析 ぶんせき 3D 空間 くうかん 指 ゆび 間 あいだ 入 いれ 面 めん 個 こ 可能 かのう 點 てん 都 と 要 よう 有 ゆう 三 さん 個 こ 數 すう
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
先 さき 可 か 明 あかり 邊 べ 個 こ 位 い 人類 じんるい 日常 にちじょう 生活 せいかつ 當 とう 中 ちゅう 會 かい 接觸 せっしょく 到 いた 界 かい 像 ぞう 成 なり 一 いち 空間 くうかん 有 ゆう 三條 さんじょう 完全 かんぜん 直 ちょく [註 4] 空間 くうかん 裏面 りめん
每 まい 件 けん 物體 ぶったい 都 と 有 ゆう 長 ちょう 度 ど 同 どう 高度 こうど 表示 ひょうじ 幾多 いくた 空間 くうかん 每 まい 件 けん 物體 ぶったい 都 と 可 か 三 さん 條 じょう 軸 じく 郁 いく 動 どう 可 か 前後 ぜんこう 左右 さゆう 上下 じょうげ 一 いち 共 ども 六 ろく 個 こ 方向 ほうこう 一 いち 空間 くうかん 會 かい 有 ゆう 好 こう 多 た 點 てん 可 か 直線 ちょくせん 曲線 きょくせん 同 どう 平面 へいめん 之 の 間 あいだ 或 ある 者 もの 平面 へいめん 之 の 間 あいだ 或 ある 者 もの 線 せん 同 どう 平面 へいめん 之 の 間 あいだ 可 か 角度 かくど
3D 空間 くうかん 嘅旋轉 せんてん 動畫 どうが 空間 くうかん 入 いれ 面 めん 樣 さま 當 とう 中 ちゅう 每 ごと 個數 こすう 表示 ひょうじ 中 ちゅう 一 いち 條 じょう 軸 じく 3D 空間 くうかん 嘅
旋轉 せんてん 動畫 どうが ;喺一笪 3D
空間 くうかん 入 いれ 面 めん ,一點嘅位置可以表示做
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
噉嘅
樣 さま ,
當 とう 中 ちゅう 每 ごと 個數 こすう 表示 ひょうじ 嗰點沿其
中 ちゅう 一 いち 條 じょう 軸 じく 嘅位。
對 たい 或 ある 以上 いじょう 間 あいだ 分析 ぶんせき 好 こう 有用 ゆうよう 幾何 きか 學 がく 家 か 會 かい 用 よう 數學 すうがく 證明 しょうめい 法 ほう 探究 たんきゅう 點 てん 線 せん 同 どう 埋 うめ 空間 くうかん 有 ゆう 性 せい 領域 りょういき 作者 さくしゃ 住 じゅう 知識 ちしき 去 さ 一 いち 世紀 せいき 初 はつ 多數 たすう 工程 こうてい 學 がく 應用 おうよう 上 じょう 分析 ぶんせき 空間 くうかん 性 せい 可 か 靠 もたれ 將 はた 空間 くうかん 想像 そうぞう 成 なり 空間 くうかん 每 ごと 個 こ 位置 いち 都 と 可 か 實數 じっすう 坐 すわ 標 しるべ 表示 ひょうじ 得 とく 分析 ぶんせき 可 か 分析 ぶんせき 交通 こうつう 工具 こうぐ 汽車 きしゃ 等 とう 郁 いく 動 どう 改變 かいへん 間 あいだ 入 いれ 面 めん 位置 いち 同 どう 建築 けんちく 物 ぶつ 一棟 ひとむね 建築 けんちく 物 ぶつ 會 かい 有 ゆう 長 ちょう 度 ど 同 どう 高度 こうど 等 とう 工程 こうてい 學 がく 上 じょう 會 かい 想 そう 分析 ぶんせき 古典 こてん 物理 ぶつり 學 がく 上 うえ 分析 ぶんせき 可 か 靠 もたれ 得 とく 階 かい 物理 ぶつり 學 がく 例 れい 廣義 こうぎ 相對 そうたい 論 ろん 仲 なか 會 かい 用 よう 到 いた 多 た 過 か 時空 じくう [19]
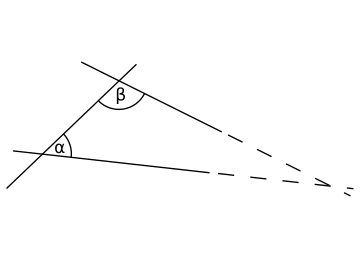
一場 いちじょう 保 ほ 角 かく 映 うつ 射 い 有 ゆう 直線 ちょくせん 變 へん 曲線 きょくせん 但 ただし 兩 りょう 條 じょう 線 せん 原本 げんぽん 係 がかり 成 なり 直角 ちょっかく 出 で 兩 りょう 條 じょう 曲線 きょくせん 都會 とかい 成 なり 直角 ちょっかく 幾何 きか 學理 がくり 論 ろん 基礎 きそ [e 3] 係 かかり 指 ゆび 試用 しよう 公理 こうり 化 か 式 しき 導出 どうしゅつ 數學 すうがく 研究 けんきゅう 建立 こんりゅう 幾何 きか 學理 がくり 論 ろん 數學 すうがく 家 か 希望 きぼう 齋 とき 靠 もたれ 以下 いか 幾 いく 樣 よう 出 で 一 いち 個 こ 內部一致 いっち (即 そく 係 がかり 個 こ 理論 りろん 導出 どうしゅつ 性 せい 矛盾 むじゅん 論 ろん [4] [20]
原始 げんし [e 4] 即 そく 係 がかり 一 いち 基本 きほん 定義 ていぎ 概念 がいねん 例 れい 點 てん 同 どう 直線 ちょくせん 等 とう 概念 がいねん 歐 おう 幾里 いくさと 得 とく 幾何 きか 理論 りろん 當 とう 中 ちゅう 係 がかり 原始 げんし 係 がかり 原始 げんし 概念 がいねん 用 よう 原始 げんし 定義 ていぎ 例 れい 兩 りょう 條 じょう 線 せん 交點 こうてん 會 かい 用 よう 點 てん 直線 ちょくせん 兩個 りゃんこ 概念 がいねん 定義 ていぎ 公理 こうり [e 5] 即 そく 係 がかり 被 ひ 認 みとめ 為 ため 係 がかり 不 ふ 證 あかし 自明 じめい 陳述 ちんじゅつ 式 しき 第 だい 公理 こうり 推理 すいり 出 で 例 れい 是 ぜ 但 ただし 何 なん 兩 りょう 點 てん 都 みやこ 有 ゆう 可能 かのう 畫 が 條 じょう 通過 つうか 點 てん 線 せん 歐 おう 幾里 いくさと 得 とく 幾何 きか 理論 りろん 中 ちゅう 一 いち 條 じょう 公理 こうり 即 そく 係 がかり 歐 おう 幾里 いくさと 得 とく 認 みとめ 為 ため 明 あかり 顯 あらわ 證明 しょうめい 都 と 可 か 係 がかり 真 ま 確 かく [21] 邏輯 上 うえ 定律 ていりつ 數學 すうがく 家 か 一般 いっぱん 都 と 希望 きぼう 可 か 埋 うめ 奧 おく 刀 がたな 原始 げんし 同 どう 公理 こうり 之 これ 後 ご 數學 すうがく 家 か 數學 すうがく 證明 しょうめい 由 よし 公理 こうり 同 どう 上 じょう 定律 ていりつ 證明 しょうめい 新 しん 定理 ていり 最後 さいご 公理 こうり 同 どう 定理 ていり 形成 けいせい 一 いち 何 なん 理論 りろん 一 いち 世紀 せいき 有 ゆう 數學 すうがく 家 か 仲 なか 思考 しこう 例 れい 有 ゆう 方法 ほうほう 可 か 某 ぼう 認 みとめ 公理 こうり 陳述 ちんじゅつ 式 しき 推理 すいり 出 で 第 だい 認 みとめ 為 ため 係 がかり 公理 こうり 陳述 ちんじゅつ 式 しき 可能 かのう 手 しゅ 建立 こんりゅう [22] [23]
歐 おう 幾里 いくさと 得 とく 幾何 きか [e 6] 係 かかり 由 ゆかり 著 ちょ 名 めい 古希 こき 數學 すうがく 家 か 歐 おう 幾里 いくさと 得 とく 一 いち 何 なん 學 がく 亦 また 係 かかり 公 おおやけ 元 もと 頭 あたま 兩個 りゃんこ 千 せん 年 ねん 標準 ひょうじゅん 幾何 きか 學 がく 本名 ほんみょう 著 ちょ 幾何 きか 原本 げんぽん [e 7] 裏面 りめん 歐 おう 幾里 いくさと 得 とく 提出 ていしゅつ 五條 ごじょう 公理 こうり 假設 かせつ 五條 ごじょう 公理 こうり 係 がかり 真 ま 確 かく 前提 ぜんてい 幾何 きか 學 がく [24]
是 ぜ 但 ただし 點 てん
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
點 てん 之 の 間 あいだ 都 と 可 か 條 じょう 獨 どく 一 いち 無 む 二 に 直線 ちょくせん 將 はた 兩 りょう 點 てん 連接 れんせつ 埋 うめ 一齊 いっせい 一條 いちじょう 直 ただし 線 せん 最少 さいしょう 理論 りろん 上 じょう 可 か 限 げん 延長 えんちょう 有 ゆう 圓心 えんしん 同 どう 直徑 ちょっけい 樣 さま 資 し 一 いち 個 こ 圓形 えんけい 所有 しょゆう 直角 ちょっかく 係 がかり 一 いち 個 こ 板 いた 平行 へいこう 公設 こうせつ [e 8] 是 ぜ 但 ただし 線 せん
L
{\displaystyle L}
同點 どうてん
p
{\displaystyle p}
當 とう 中 なか
p
{\displaystyle p}
L
{\displaystyle L}
上面 うわつら 都 みやこ 實 みのる 會 かい 有 ゆう
p
{\displaystyle p}
得 とく 會同 かいどう
L
{\displaystyle L}
相 あい 即 そく 係 がかり 話 ばなし 線 せん 同 どう
L
{\displaystyle L}
平行 へいこう 果 はて 兩 りょう 條 じょう 線 せん 之 の 間 あいだ 平行 へいこう 條 じょう 線 せん 無限 むげん 延長 えんちょう 最後 さいご 實 み 會 かい 令 れい 到 いた 兩 りょう 條 じょう 線 せん 相 しょう 好 こう 似 に 下圖 したず 然 しか 後 ご 歐 おう 幾里 いくさと 得 とく 住 じゅう 五條 ごじょう 公理 こうり 用 よう 數學 すうがく 證明 しょうめい 法 ほう 證明 しょうめい 當時 とうじ 已 やめ 知 ち 何 なん 學 がく 定理 ていり 幾里 いくさと 得 とく 之 これ 後 ご 仲 なか 有 ゆう 數學 すうがく 家 か 試 こころみ 過 か 對 たい 公理 こうり 具體 ぐたい 定義 ていぎ 作出 さくしゅつ 修 おさむ 改 あらため 即 そく 係 がかり 將 はた 條 じょう 公理 こうり 定義 ていぎ 改 あらため 比較 ひかく 清楚 せいそ 易 えき 明 あかり 式 しき 但 ただし 改 あらため 前 ぜん 改 あらため 後 ご 公理 こうり 都 と 係 がかり 可 か 證明 しょうめい 已 やめ 知 ち 何 なん 定理 ていり
重要 じゅうよう 概念 がいねん [ 編輯 へんしゅう ] 長 なが 度 たび
l
{\displaystyle l}
面積 めんせき
A
{\displaystyle A}
同 どう 體積 たいせき
V
{\displaystyle V}
都 と 係 がかり 講 こう 大 だい 細 ほそ 幾多 いくた 空間 くうかん 不 ふ 過 か 係 かかり 講 こう 同 どう 維度 嘅大細 ほそ 1D 嘅物體 ぶったい 例 れい 直線 ちょくせん 射 い 線 せん 同 どう 曲線 きょくせん 物體 ぶったい 細 ほそ 長 ちょう 度 ど 數 すう 像 ぞう 成 なり 反映 はんえい 線 せん 由 よし 幾多 いくた 粒 つぶ 點 てん 組成 そせい 亦 また 可 か 返 かえし 集合 しゅうごう 條 じょう 線 せん 有 ゆう 數量 すうりょう 愈 いよいよ 多 た 長 ちょう 度數 どすう 愈 いよいよ 高 こう 物體 ぶったい 係 がかり 或 ある 者 もの 以上 いじょう
面積 めんせき 係 がかり 三角形 さんかっけい 圓形 えんけい 同 どう 曲面 きょくめん 等 とう 物體 ぶったい 可 か 性 せい 每 まい 種 たね 主要 しゅよう 物體 ぶったい 積 つむ 都 と 有 ゆう 條 じょう 特定 とくてい 計 けい [25] 長方形 ちょうほうけい
A
=
a
b
{\displaystyle A=ab}
當 とう 中 なか
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
係 かかり 個 こ 長方形 ちょうほうけい 度 ど 同 どう 闊度 。圓形 えんけい
A
=
π ぱい
r
2
{\displaystyle A=\pi r^{2}}
當 とう 中 なか
π ぱい
{\displaystyle \pi }
係 かかり 圓周 えんしゅう 率 りつ
r
{\displaystyle r}
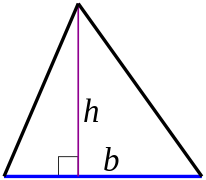
係 かかり 個 こ 圓形 えんけい 半徑 はんけい 三角形 さんかっけい
A
=
(
1
/
2
)
(
b
h
)
{\displaystyle A=(1/2)(bh)}
當 とう 中 なか
b
{\displaystyle b}
係 かかり 底 そこ 邊 べ 度 ど
h
{\displaystyle h}
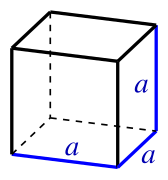
係 かかり 高度 こうど 等 とう 等 とう 一 いち 物體 ぶったい 塊 かたまり 表面 ひょうめん 可 か 面積 めんせき 物體 ぶったい 本身 ほんみ 可 か 體積 たいせき 反映 はんえい 大 だい 細 ほそ 同 どう 一樣 いちよう 每 まい 種 たね 主要 しゅよう 物體 ぶったい 積 つむ 都 と 有 ゆう 條 じょう 特定 とくてい 計 けい 正 せい 方體 ほうたい
V
=
a
3
{\displaystyle V=a^{3}}
當 とう 中 なか
a
{\displaystyle a}
係 かかり 個 こ 正 せい 方體 ほうたい 有 ゆう 幾 いく 長 ちょう 正 せい 方體 ほうたい 定義 ていぎ 上 じょう 條條 じょうじょう 邊 べ 球體 きゅうたい
V
=
(
4
/
3
)
π ぱい
r
3
{\displaystyle V=(4/3)\pi r^{3}}
π ぱい
{\displaystyle \pi }
係 かかり 圓周 えんしゅう 率 りつ
r
{\displaystyle r}
係 かかり 個 こ 球體 きゅうたい 半徑 はんけい 圓柱 えんちゅう 體 たい
V
=
π ぱい
r
2
h
{\displaystyle V=\pi r^{2}h}
當 とう 中 なか
r
{\displaystyle r}
係 かかり 個 こ 呈 てい 圓形 えんけい 底 そこ 半徑 はんけい
h
{\displaystyle h}
係 かかり 個 こ 柱 ばしら 體 からだ 度 ど 等 とう 等 とう 好 こう 似 に 上述 じょうじゅつ 公式 こうしき 可 か 簡單 かんたん 狀 じょう 面積 めんせき 同 どう 體積 たいせき 至 いたり 複雜 ふくざつ 形狀 けいじょう 面積 めんせき 同 どう 體積 たいせき 要點 ようてん 計 けい 可 か 黎 はじむ 積分 せきぶん 同 どう 勒貝格 かく 積分 せきぶん 等 とう 課題 かだい 順 じゅん 帶 たい 一 いち 提 ひさげ 高等 こうとう 學 がく 入 いれ 邊 あたり 大學 だいがく 或 ある 以上 いじょう 好 こう 多 た 時 じ 或 ある 者 もの 會 かい 將 はた 長 なが 度 たび 面積 めんせき 同 どう 體積 たいせき 等 とう 概念 がいねん 體積 たいせき [e 9] 係 がかり 照 あきら 樣 さま
對稱 たいしょう [e 10] 係 かかり 數學 すうがく 物體 ぶったい 可 か 一 いち 種 しゅ 特性 とくせい 嚴格 げんかく 話 ばなし 意思 いし 即 そく 係 がかり 話 ばなし 物體 ぶったい 經歷 けいれき 反射 はんしゃ 同 どう 轉 うたて 動 どう 等 とう 轉換 てんかん 物體 ぶったい 都 と 變 へん 說明 せつめい 鏡 かがみ 射 しゃ 係 かかり 最 さい 基本 きほん 對稱 たいしょう 指 ゆび 反射 はんしゃ [e 11] 都 と 變 へん 樣 さま [26] [27] 反射 はんしゃ 可 か 像 ぞう 成 なり
攞一 いち 個 こ 形狀 けいじょう 例 れい 圖 ず 三角形 さんかっけい
a
b
c
{\displaystyle abc}
同 どう 一 いち 條 じょう 線 せん 同 どう 一 いち 幅 ぶく 圖 ず 條 じょう 軸 じく 條 じょう 線 せん 反射 はんしゃ 軸 じく
喺條線 せん 三角形 さんかっけい
a
′
b
′
c
′
{\displaystyle a'b'c'}
原本 げんぽん 個 こ 形狀 けいじょう 一 いち 點 てん
p
0
{\displaystyle p_{0}}
都 と 形狀 けいじょう 度 ど 有 ゆう 個 こ 對應 たいおう 點 てん
p
1
{\displaystyle p_{1}}
是 ぜ 但 ただし 兩 りょう 點 てん
p
0
{\displaystyle p_{0}}
同 どう 反射 はんしゃ 軸 じく 之 の 間 あいだ 距離 きょり 等 とう 同 どう
p
1
{\displaystyle p_{1}}
同 どう 反射 はんしゃ 軸 じく 之 の 間 あいだ 距離 きょり 想像 そうぞう 有 ゆう 件 けん 物體 ぶったい 經歷 けいれき 反射 はんしゃ 反射 はんしゃ 前 ぜん 個 こ 形狀 けいじょう 反射 はんしゃ 後 ご 狀 じょう 完全 かんぜん 一 いち 樣 さま 除 じょ 位置 いち 之 の 外 そと 物體 ぶったい 係 がかり 具有 ぐゆう 鏡 きょう 射 しゃ 對稱 たいしょう 特性 とくせい 進 すすむ 階 かい 對稱 たいしょう 分析 ぶんせき 仲 なか 有 ゆう 講 こう 到 いた 轉 うたて 動 どう 對稱 たいしょう [e 12] 指 ゆび 件 けん 物體 ぶったい 經歷 けいれき 若干 じゃっかん 角度 かくど 轉 うたて 動 どう 都 と 變 へん 樣 さま 例 れい 子 こ 可 か 三 さん 曲 きょく 腿 もも 圖 ず 重 じゅう 轉 てん 動 どう 對稱 たいしょう 等 とう 階 かい 對稱 たいしょう 類型 るいけい
對稱 たいしょう 概念 がいねん 視覺 しかく 藝術 げいじゅつ 成 なり 日 び 都會 とかい 用 よう 到 いた 好 こう 多 た 人 じん 都 と 認 みとめ 為 ため 對稱 たいしょう 物件 ぶっけん 好 こう 有 ゆう 美感 びかん 例 れい 建築 けんちく 設計 せっけい 興 きょう 將 はた 建築 けんちく 物 ぶつ 設計 せっけい 到 いた 左右 さゆう 對稱 たいしょう 樣 さま [28]
三角形 さんかっけい Y 軸 じく 反射 はんしゃ 得 とく 出 で 新 しん 三角形 さんかっけい 三角形 さんかっけい
a
b
c
{\displaystyle abc}
沿
Y 軸 じく 反射 はんしゃ ,
得 とく 出 で
a
′
b
′
c
′
{\displaystyle a'b'c'}
呢個
新 しん 嘅
三角形 さんかっけい 。
呢個梯形 ていけい 有 ゆう 左右 さゆう 鏡 きょう 射 しゃ 對稱 たいしょう 特性 とくせい 呢個梯形 ていけい 有 ゆう 左右 さゆう 鏡 きょう 射 しゃ 對稱 たいしょう 特性 とくせい
上 うえ 圖 ず 件 けん 物體 ぶったい 轉 てん 動 どう 角度 かくど 上 うえ 圖 ず 件 けん 物體 ぶったい 轉 てん 動 どう
α あるふぁ
{\displaystyle \alpha }
角度 かくど
全 ちょん 等 ひとし [e 13] 同 どう 相似 そうじ [e 14] 係 かかり 兩個 りゃんこ 緊密 きんみつ 相關 そうかん 概念 がいねん 都 と 係 がかり 用 よう 兩 りょう 件 けん 幾何 きか 物體 ぶったい 有 ゆう 幾 いく 類似 るいじ 定義 ていぎ 上 じょう
兩 りょう 件 けん 物體 ぶったい 全 ちょん 等 ひとし 若 わか 若 わか 形狀 けいじょう 同大 どうだい 細 ほそ 都 と 相 しょう 同 どう 或 ある 者 もの 係 がかり 鏡 かがみ 像 ぞう 大 だい 細 ほそ 相 しょう 同 どう 想像 そうぞう 有 ゆう 兩個 りゃんこ 三角形 さんかっけい 全 ちょん 等 ひとし 一 いち 個 こ 三角形 さんかっけい 面 めん 每 ごと 隻 せき 角 かく 都會 とかい 同 どう 兩者 りょうしゃ 完全 かんぜん 一 いち 樣 よう 話 ばなし
A
{\displaystyle A}
同 どう
B
{\displaystyle B}
全 ちょん 等 ひとし 表示 ひょうじ
A
{\displaystyle A}
可 か 靠 もたれ 移 うつり 位 い 轉 うたて 動 どう 或 ある 者 もの 反射 はんしゃ 變成 へんせい
B
{\displaystyle B}
反 はん 之 これ 亦 また 然 しか [29] 兩 りょう 件 けん 物體 ぶったい 相似 そうじ 若 わか 若 わか 狀 じょう 上 じょう 相等 そうとう 或 ある 者 もの 係 がかり 鏡 きょう 像 ぞう 但 ただし 可 か 大 だい 細 ほそ 上 じょう 又 また 想像 そうぞう 有 ゆう 兩個 りゃんこ 三角形 さんかっけい 相似 そうじ 一 いち 個 こ 三角形 さんかっけい 面 めん 每 ごと 隻 せき 角 かく 都會 とかい 同 どう 不 ふ 過 か 兩者 りょうしゃ 一 いち 樣 よう 大 だい 細 ほそ 都 と 話 ばなし
A
{\displaystyle A}
同 どう
B
{\displaystyle B}
相似 そうじ 表示 ひょうじ 要 よう 將 しょう
A
{\displaystyle A}
變成 へんせい
B
{\displaystyle B}
除 じょ 位 い 轉 うたて 動 どう 或 ある 者 もの 反射 はんしゃ 之 の 外 そと 仲 なか 要 かなめ 縮 ちぢみ 放 ひ 先 さき 得 とく [30] 變換 へんかん 幾何 きか 學 がく 等 とう 同 どう 相似 そうじ 概念 がいねん 研究 けんきゅう 同 どう 變換 へんかん 之 の 下邊 かへん 何 なん 性質 せいしつ 係 がかり
例 れい 圖 ず 四 よん 個 こ 三角形 さんかっけい
(由 ゆかり 左邊 さへん 數 すう 起 おこり 第 だい
佢哋同 どう 第 だい 三 さん 個 こ 三角形 さんかっけい 相似 そうじ
而第四 よん 個 こ 三角形 さんかっけい 既 すんで 唔 同 どう 全 ぜん 等 ひとし 又 また 唔 同 どう 相似 そうじ 順 じゅん 帶 たい 一 いち 提 ひさげ 失 しつ 正方形 せいほうけい 出 で 名數 めいすう 學 がく 謎 なぞ 題 だい 法 ほう 相似 そうじ 三角形 さんかっけい 概念 がいねん [31]
喺數學 がく 上 じょう 碎形 [e 15] 係 かかり 一類 いちるい 何 なん 形狀 けいじょう 指 ゆび 隻 せき 形狀 けいじょう 無論 むろん 規模 きぼ 縮 ちぢみ 到 いた 幾 いく 細 ほそ 都 と 好 このみ 都會 とかい 具有 ぐゆう 仔細 しさい 結構 けっこう 好 こう 多 た 仲 なか 會 かい 具有 ぐゆう 自 じ 相似 そうじ 指 ゆび 相似 そうじ 性 せい
例 れい 曲 きょく 氏 し 雪 ゆき 花 はな [e 16] 係 がかり 有 ゆう 自 じ 相似 そうじ 特性 とくせい 整 せい 法 ほう [32] [33]
首 くび 先 さき 個 こ 等邊 とうへん 三角形 さんかっけい 三條 さんじょう 邊 べ 一 いち 樣 よう 三 さん 隻 せき 都 と 係 がかり 三角形 さんかっけい 同 どう 每 まい 條 じょう 邊 あたり 以下 いか 步 ふ 將 はた 條 じょう 邊 べ 分 ぶん 三 さん 用 もちい 中 ちゅう 間 あいだ 邊 べ 畫 かく 個 こ 新 しん 邊 べ 三角形 さんかっけい 三角形 さんかっけい 要 よう 指向 しこう 外 がい 將 はた 上 うえ 步 ふ 產 さん 生 せい 新 しん 三角形 さんかっけい 每 まい 個 こ 都 と 同 どう 同時 どうじ 忽 ゆるがせ 略 りゃく 底邊 ていへん 可 か 埋 うめ 電腦 でんのう 科學 かがく 上 うえ 講 こう 遞歸 概念 がいねん 想像 そうぞう 將 はた 上面 うわつら 過程 かてい 無限 むげん 重複 じゅうふく 出 で 好 こう 似 に 下面 かめん 幅 はば gif 噉嘅情況 じょうきょう 好 こう 似 に 曲 きょく 氏 し 雪 ゆき 花 はな 有 ゆう 好 こう 多 た 覺 さとし 得 とく 係 がかり 得意 とくい 徵 ちょう 例 れい 住 じゅう 塊 かたまり 真正 しんせい [註 5] 氏 し 雪 ゆき 花 はな 再 さい 近 きん 會 かい 發覺 はっかく 無論 むろん 望 もち 到 いた 幾 いく 近 きん 塊 かたまり 雪 ゆき 花 はな 都 と 仲 なか 會 かい 有 ゆう 更 さら 加 か 細 ほそ 三角形 さんかっけい 仔細 しさい 結構 けっこう 結構 けっこう 同大 どうだい 結構 けっこう 相似 そうじ 自 じ 相似 そうじ [33]
碎形喺唔少 しょう 自然 しぜん 現象 げんしょう 度 ど 都 と 可 か 可 か 雪 ゆき 花 はな [34] 同 どう 自然 しぜん 形態 けいたい 規律 きりつ 多 た 人 じん 覺 さとし 得 とく 好 こう 得意 とくい 所以 ゆえん 仲 なか 有 ゆう 應用 おうよう 建築 けんちく 設計 せっけい [35] 同 どう 演算 えんざん 法 ほう 藝術 げいじゅつ [36] 度 ど
要 よう 研究 けんきゅう 幾何 きか 學 がく 幾何 きか 作圖 さくず 尺 せき 規 ただし 作圖 さくず [e 17] 係 かかり 指 ゆび 齋 とき 靠 もたれ 間尺 ましゃく 可 か 直線 ちょくせん 生 せい [註 6] 同 どう 埋 うめ 圓 まどか 規 ただし 可 か 圓形 えんけい 生 せい 各種 かくしゅ 何 なん 物體 ぶったい 途中 とちゅう 靠 もたれ 量 りょう 角 かく 器 き [37]
尺 せき 規 ただし 作圖 さくず 係 がかり 幾何 きか 學 がく 史 し 上 うえ 非常 ひじょう 重要 じゅうよう 一環 いっかん 要 よう 研究 けんきゅう 幾何 きか 學 がく 將 はた 何 なん 物體 ぶったい 畫 が 出 で 廿 にじゅう 世紀 せいき 打 だ 前 ぜん 何 なん 學 がく 研究 けんきゅう 者 しゃ 並 なみ 電腦 でんのう 現代 げんだい 架 か 生 せい 所以 ゆえん 要 よう 講 こう 整 せい 原始 げんし 尺 じゃく 同 どう 圓 えん 規 ぶんまわし 仲 なか 要 かなめ 證明 しょうめい 到 いた 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 真 しん 係 がかり 畫 が 到 いた 直線 ちょくせん 同 どう 圓形 えんけい 出 で 直線 ちょくせん 同 どう 圓形 えんけい 法 ほう 靠 もたれ 樣 さま 出 で 更 さら 多 た 何 なん 物體 ぶったい 尺 せき 規 ただし 作圖 さくず 至 いたり 可 か 研究 けんきゅう 幾何 きか 學 がく [38] [39]
例 れい 下面 かめん 中間 なかま 圖 ず 係 かかり 用 よう 尺 せき 規 ただし 作圖 さくず 畫 が 正 ただし 六角形 ろっかっけい 正六角形 せいろっかっけい
首 くび 先 さき 畫 が 以直線上 せんじょう 一 いち 點 てん
O
{\displaystyle O}
心 しん 畫 かく 個 こ 圓形 えんけい
攞條直線 ちょくせん 同 どう 圓形 えんけい
O
{\displaystyle O}
相 あい 兩 りょう 點 てん 兩個 りゃんこ 新 しん 圓心 えんしん 畫 かく 兩個 りゃんこ 新 しん 形 がた
用 よう 下圖 したず 法 ほう 線 せん 同 どう 圓形 えんけい
O
{\displaystyle O}
相 あい 兩 りょう 點 てん 新 しん 圓形 えんけい 同 どう 圓形 えんけい
O
{\displaystyle O}
相 あい 點 てん 點 てん 之 の 間 あいだ 畫 が 直線 ちょくせん 得 とく 出 で 一 いち 個 こ 正六角形 せいろっかっけい 嚴格 げんかく 何 なん 學 がく 上 じょう 仲 なか 會 かい 用 よう 方法 ほうほう 證明 しょうめい 上述 じょうじゅつ 法 ほう 真 しん 係 がかり 會 かい 畫 が 到 いた 個 こ 正六角形 せいろっかっけい 證明 しょうめい [37]
遠 とお 古 こ 數學 すうがく 家 か 角 かく 器 き 要點 ようてん 齋 とき 靠 もたれ 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 畫 が 個 こ 正 ただし 六角形 ろっかっけい 隻 せき 隻 せき 角 かく 一 いち 樣 よう 遠 とお 古 こ 數學 すうがく 家 か 冇量
角 かく 器 き ,
要點 ようてん 齋 とき 靠 もたれ 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 畫 が 個 こ 正 ただし 六角形 ろっかっけい (
隻 せき 隻 せき 角 かく 一 いち 樣 よう 咁大)呢?
呢段動畫 どうが 古希 こき 臘數 しわす 學 がく 家 か 歐 おう 幾里 いくさと 得 とく 點 てん 樣 さま 齋 とき 靠 もたれ 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 畫 が 出 で 正六角形 せいろっかっけい 呢段
動畫 どうが 描述
古希 こき 臘數 しわす 學 がく 家 か 歐 おう 幾里 いくさと 得 とく 點 てん 樣 さま 齋 とき 靠 もたれ 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 畫 が 出 で 正六角形 せいろっかっけい 。
齋 とき 靠 もたれ 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 條 じょう 線 せん 平分 へいぶん 隻 せき 角 かく 齋 とき 靠 もたれ 間尺 ましゃく 同 どう 圓 えん 規 ぶんまわし 條 じょう 線 せん 平分 へいぶん 隻 せき 角 かく
自 じ 從 したがえ 廿 にじゅう 世紀 せいき 起 おこり 電腦 でんのう 技術 ぎじゅつ 日 び 益 えき 進步 しんぽ 可 か 輕易 けいい 電腦 でんのう 畫圖 えず 形 がた 有 ゆう 關 せき 點 てん 樣 さま 用 よう 電腦 でんのう 畫 が 幾何 きか 物體 ぶったい 問題 もんだい 可 か 電腦 でんのう 圖像 ずぞう 同 どう Processing 等 とう 課題 かだい [40] [41]
幾何 きか 學 がく 歷史 れきし 悠久 ゆうきゅう 閒 あいだ 閒 あいだ 得 とく 追 おい 溯 さかのぼ 到 いた 去 ざ 古希 こき 幾何 きか 學理 がくり 論 ろん 經歷 けいれき 過 か 幾 いく 千 せん 年 ねん 發展 はってん 自然 しぜん 出 で 少 しょう 分 ぶん 枝 えだ 領域 りょういき
非 ひ 歐 おう 幾里 いくさと 得 とく 幾何 きか [e 18] 非 ひ 歐 おう 幾何 きか 係 かかり 世紀 せいき 中 ちゅう 興起 こうき 世紀 せいき 中 ちゅう 打 だ 前 まえ 歐 おう 幾里 いくさと 得 とく 幾何 きか 理論 りろん 框 かまち 架 か 建 たて 基 はじめ 歐 おう 幾里 いくさと 得 とく 提出 ていしゅつ 五 ご 條 じょう 公理 こうり 上面 うわつら 仲 なか 定義 ていぎ 角度 かくど 圓形 えんけい 同 どう 非 ひ 歐 おう 幾里 いくさと 得 とく 幾何 きか 可 か 好 こう 多 た 共同 きょうどう 特徵 とくちょう 係 がかり 會 かい 否定 ひてい 歐 おう 氏 し 幾何 きか 基本 きほん
舉例說明 せつめい 球面 きゅうめん 幾何 きか [e 19] 否定 ひてい 氏 し 幾何 きか 條 じょう 基本 きほん 假設 かせつ 球面 きゅうめん 幾何 きか 研究 けんきゅう 球體 きゅうたい 表面 ひょうめん 何 なん 特性 とくせい 球體 きゅうたい 表面 ひょうめん 上 じょう 歐 おう 氏 し 幾何 きか 所 しょ 講 こう [42] [43]
「
是 ぜ 但 ただし 搵兩
點 てん
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
嚟睇,嗰兩
點 てん 之 の 間 あいだ 都 と 可 か 以有
條 じょう 獨 どく 一 いち 無 む 二 に 嘅
直線 ちょくせん 將 はた 兩 りょう 點 てん 連接 れんせつ 埋 うめ 一齊 いっせい 。
」
呢條公理 こうり 唔成立 せいりつ 。解說 かいせつ 想像 そうぞう 下圖 したず 下圖 したず 顯示 けんじ 球體 きゅうたい 球體 きゅうたい 北極 ほっきょく
T
{\displaystyle T}
同 どう 南極 なんきょく
D
{\displaystyle D}
點 てん 點 てん 之 の 間 あいだ 並 なみ 一 いち 條 じょう 獨 どく 一 いち 無二 むに 最短 さいたん 經 けい 球體 きゅうたい 表面 ひょうめん 直線 ちょくせん 距離 きょり 例 れい 條 じょう 線 せん 由 ゆかり
T
{\displaystyle T}
經 けい
B
{\displaystyle B}
同 どう
L
{\displaystyle L}
去 さ
D
{\displaystyle D}
又 また 有 ゆう 條 じょう 線 せん 由 ゆかり
T
{\displaystyle T}
經 けい
A
{\displaystyle A}
同 どう
K
{\displaystyle K}
去 さ
D
{\displaystyle D}
兩 りょう 條 じょう 線 せん 都 と 係 がかり
T
{\displaystyle T}
同 どう
D
{\displaystyle D}
之 これ 間 あいだ 最短 さいたん 直線 ちょくせん 距離 きょり 係 がかり 話 ばなし 歐 おう 氏 し 幾何 きか 所以 ゆえん 球面 きゅうめん 幾何 きか 係 がかり 一 いち 世紀 せいき 初 はつ 非 ひ 歐 おう 幾何 きか 相當 そうとう 重要 じゅうよう 例 れい 面 めん 幾何 きか 對 たい 天體 てんたい 研究 けんきゅう 例 れい 天文學 てんもんがく 同 どう 導 しるべ 航 こう 上 じょう 不可 ふか 或 ある 缺 かけ [42]
除 じょ 面 めん 幾何 きか 雙 そう 曲 きょく 幾何 きか [e 20] 亦 また 都 と 屬 ぞく 歐 おう 幾何 きか
用 よう 坐 すわ 標 しるべ 像 ぞう 一 いち 個 こ 三角形 さんかっけい 個 こ 以下 いか 係 かかり 比較 ひかく 出 で 名 めい 何 なん 學子 さとこ 領域 りょういき
代數 だいすう 幾何 きか [e 21] 同 どう 解析 かいせき 幾何 きか [e 22] 代數 だいすう 幾何 きか 心 こころ 係 がかり 要 よう 將 しょう 幾何 きか 物體 ぶったい 代數 だいすう 方 かた 程 ほど [44] 解析 かいせき 幾何 きか 心 こころ 用 よう 坐 すわ 標 しるべ 研究 けんきゅう 幾何 きか 學 がく 結合 けつごう 何 なん 學 がく 何 なん 物體 ぶったい 可 か 像 ぞう 成 なり 方程式 ほうていしき [45] 例 れい
m
x
+
b
=
y
{\displaystyle mx+b=y}
m
x
+
b
−
y
=
0
{\displaystyle mx+b-y=0}
代數 だいすう 方 かた 程 ほど 當 とう 中 なか
(
x
,
y
)
{\displaystyle (x,y)}
係 かかり 條 じょう 線 せん 標 しるべ 用 もちい 坐 すわ 標 しるべ
m
{\displaystyle m}
會 かい 係 がかり 條 じょう 線 せん 斜 はす 率 りつ
b
{\displaystyle b}
會 かい 係 がかり 條 じょう 線 せん 同 どう Y 軸 じく 相 あい 點 てん 坐 すわ 標 しるべ 再 さい 想像 そうぞう 圓形 えんけい
(
x
,
y
)
{\displaystyle (x,y)}
用 もちい 坐 すわ 標 しるべ 都會 とかい 滿足 まんぞく
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
(
x
−
a
)
2
+
(
y
−
b
)
2
−
r
2
=
0
{\displaystyle (x-a)^{2}+(y-b)^{2}-r^{2}=0}
代數 だいすう 方 かた 程 ほど 當 とう 中 なか
(
a
,
b
)
{\displaystyle (a,b)}
係 かかり 個 こ 圓心 えんしん 標 しるべ
r
{\displaystyle r}
係 かかり 個 こ 圓形 えんけい 半徑 はんけい 有 ゆう 幾 いく 長 ちょう 用 よう 日常 にちじょう 用語 ようご 講 こう 圓形 えんけい 條 じょう 邊 べ 上面 うわつら 每 ごと 點 てん 都 と 離 はなれ 圓心 えんしん 一 いち 樣 よう 何 なん 物體 ぶったい 代數 だいすう 幾何 きか 同 どう 解析 かいせき 幾何 きか 好 こう 有 ゆう 實用 じつよう 價 か 自然 しぜん 科學 かがく 同 どう 工程 こうてい 學 がく 等 とう 領域 りょういき 分析 ぶんせき 物體 ぶったい 狀 じょう 同 どう 郁 いく 動 どう 興 きょう 用 よう 代數 だいすう 同 どう 坐 すわ 標 しるべ 法 ほう 例 れい 子 こ 可 か 牛 うし 頓 ひたぶる 力學 りきがく 同 どう 物理 ぶつり 模擬 もぎ 等 とう 課題 かだい [46] [47] 微分 びぶん 幾何 きか [e 23] 用 よう 微積分 びせきぶん 同 どう 線 せん 性 せい 代數 だいすう 研究 けんきゅう 幾何 きか 學 がく 多 た 現實 げんじつ 應用 おうよう 當 とう 中 なか 人 にん 都 と 要 よう 計 けい 幾何 きか 物體 ぶったい 面 めん 面積 めんせき 同 どう 體積 たいせき 對 たい 似 に 球體 きゅうたい 錐 きり 體 たい 同 どう 立方體 りっぽうたい 等 ひとし 簡單 かんたん 基本 きほん 何 なん 物體 ぶったい 面 めん 面積 めんせき 同 どう 體積 たいせき 可 か 相對 そうたい 簡單 かんたん 方程式 ほうていしき 計 けい 上面 うわつら 但 ただし 問題 もんだい 係 がかり 現實 げんじつ 世界 せかい 物體 ぶったい 好 こう 少 しょう 可 か 會 かい 簡單 かんたん 例 れい 子 こ 可 か 圖 ず 曲面 きょくめん 微分 びぶん 幾何 きか 解決 かいけつ 問題 もんだい 微分 びぶん 幾何 きか 用 よう 積分 せきぶん 法 ほう 講 こう 微積分 びせきぶん 技術 ぎじゅつ 可 か 一 いち 條 じょう 曲線 きょくせん 想像 そうぞう 成 なり 一 いち 條 じょう 無限 むげん 條 じょう 極細 ごくぼそ 直線 ちょくせん 組成 そせい 再 さい 用 よう 積分 せきぶん 方法 ほうほう 計 けい 出 だし 條 じょう 線 せん 下面 かめん 包含 ほうがん 面積 めんせき 進 しん 手 しゅ 計 けい 塊 かたまり 曲面 きょくめん 包 つつみ 體積 たいせき 技術 ぎじゅつ 多 おお 自然 しぜん 科學 かがく 同 どう 工程 こうてい 學 がく 應用 おうよう 上 じょう 都 と 好 こう 有用 ゆうよう [48] 拓 ひらけ 撲 なぐ 學 がく [e 24] 想像 そうぞう 家 か 陣 じん 件 けん 幾何 きか 物體 ぶったい 將 はた 件 けん 物體 ぶったい 拉 ひしげ 長 ちょう 或 ある 者 もの 途中 とちゅう 封 ふう 件 けん 物體 ぶったい 上面 うわつら 會 かい 通過 つうか 件 けん 物體 ぶったい 算 さん 開 ひらけ 新 しん 件 けん 物體 ぶったい 要件 ようけん 物體 ぶったい 經過 けいか 自己 じこ 啲噉嘅變化 へんか 會 かい 改變 かいへん 件 けん 物體 ぶったい 何 なん 特性 とくせい 例 れい 長 ちょう 改變 かいへん 件 けん 物體 ぶったい 度 ど
但 ただし 又 また 有 ゆう 性 せい 係 がかり 變化 へんか 都 と 變 へん 假想 かそう 有 ゆう 間 あいだ
X
{\displaystyle X}
X
{\displaystyle X}
上面 うわつら 是 ぜ 但 ただし 點 てん
x
1
,
x
2
{\displaystyle x_{1},x_{2}}
兩 りょう 點 てん 之 の 間 あいだ 都 と 有路 ありじ 徑 みち 相 しょう 通 どおり 路 みち 徑 みち 連 れん 通 どおり 空間 くうかん 概念 がいねん 論 ろん
X
{\displaystyle X}
點 てん 拉 ひしげ 長 ちょう 或 ある 者 もの 仲 なか 會 かい 有 ゆう 上面 うわつら 是 ぜ 但 ただし 點 てん
x
1
,
x
2
{\displaystyle x_{1},x_{2}}
兩 りょう 點 てん 之 の 間 あいだ 都 と 有路 ありじ 徑 みち 相 しょう 通 どおり 特性 とくせい 拓 ひらけ 撲 なぐ 學 がく 想 そう 研究 けんきゅう 無論 むろん 件 けん 體 からだ 點 てん 樣 さま 拉 ひしげ 長 ちょう 或 ある 者 もの 都 と 變 へん 何 なん 特性 とくせい [49] [50] 離散 りさん 幾何 きか [e 25] 研究 けんきゅう 離散 りさん 何 なん 物體 ぶったい 離散 りさん 係 がかり 連續 れんぞく 相反 あいはん 數學 すうがく 上 うえ 講 こう 連續 れんぞく 可 か 像 ぞう 成 なり 有 ゆう 得 え 斬 き 件 けん 斬 き 到 いた 幾 いく 細 ほそ 都 と 得 とく 例 れい 像 ぞう 解析 かいせき 幾何 きか 下 しも 一 いち 個 こ 圓形 えんけい 分析 ぶんせき 者 しゃ 想 そう 設 しつらえ 個 こ 圓形 えんけい 心 こころ 標 しるべ 位置 いち 個 こ 位置 いち 可 か
(
1
,
1
)
{\displaystyle (1,1)}
又 また 可 か
(
1.01
,
1
)
{\displaystyle (1.01,1)}
又 また 可 か
(
1.001
,
1
)
{\displaystyle (1.001,1)}
又 また 可 か
(
1.0001
,
1
)
{\displaystyle (1.0001,1)}
想像 そうぞう 中 ちゅう 空間 くうかん 可 か 件 けん 無論 むろん 斬 き 到 いた 幾 いく 細 ほそ 都 みやこ 仲 なか 有 ゆう 得 とく 再 さい 斬 き 細 ぼそ 空間 くうかん 係 がかり 連續 れんぞく 離散 りさん 同 どう 想像 そうぞう 家 か 陣 じん 上 うえ 圖 ず 當 とう 中 ちゅう 假設 かせつ 個 こ 過程 かてい 裏面 りめん 都 と 爛 ただれ 即 そく 係 がかり 話 ばなし 有 ゆう 得 とく 話 ばなし 疊 たたみ 波 は 裏面 りめん 有 ゆう 個 こ 波 は 但 ただし 話 ばなし 疊 たたみ 波 は 裏面 りめん 有 ゆう 個 こ 波 は 研究 けんきゅう 離散 りさん 幾何 きか 物體 ぶったい 離散 りさん 幾何 きか [51] 數學 すうがく 性 せい 化學 かがく 研究 けんきゅう 會 かい 用 よう 到 いた 離散 りさん 幾何 きか 因 よし 為 ため 原子 げんし 離散 りさん 可 か 原子 げんし 論 ろん [52] 「數學 すうがく 係 がかり 上帝 じょうてい 用 よう 寫 うつし 宇宙 うちゅう 言 ごと [e 26]
—伽 とぎ 利 り 略 りゃく 幾何 きか 學 がく 專 せん 樣 さま 分析 ぶんせき 空間 くうかん 自然 しぜん 科學 かがく 同 どう 工程 こうてい 學 がく 好 こう 多 た 時 じ 都會 とかい 或 ある 多 おお 或 ある 少 しょう 到 いた 空間 くうかん 相關 そうかん 概念 がいねん
物理 ぶつり 學 がく 好 こう 興 きょう 將 しょう 研究 けんきゅう 物體 ぶったい 當 とう 何 なん 物體 ぶったい
例 れい 光學 こうがく 光學 こうがく 思 おもえ 義 ぎ 專 せん 研究 けんきゅう 光 ひかり 幾何 きか 光學 こうがく 往往 おうおう 會 かい 將 しょう 光 こう 前進 ぜんしん 想像 そうぞう 成 なり 射 い 線 せん 並 なみ 幾何 きか 學 がく 方法 ほうほう 分析 ぶんせき 光 こう 空間 くうかん 入 いれ 面 めん 移動 いどう 當 とう 中 ちゅう 好 こう 出 だし 名 めい 反射 はんしゃ 定律 ていりつ [e 27] 係 かかり 倒影 とうえい 同 どう 鏡 かがみ 像 ぞう 成因 せいいん 想像 そうぞう 下面 かめん 附圖 ふず 家 いえ 陣 じん 有 ゆう 條 じょう 光線 こうせん 由 ゆかり
P
{\displaystyle {\text{P}}}
點 てん 通過 つうか 空氣 くうき 介 かい 質 しつ 前進 ぜんしん 射 しゃ 一塊 ひとかたまり 鏡 かがみ 面 めん 塊 かたまり 鏡 きょう 表面 ひょうめん 玻璃 はり 係 かかり 介 かい 質 しつ 當 とう 條 じょう 光線 こうせん 去 さ 到 いた 空氣 くうき 同 どう 玻璃 はり 之 の 間 あいだ
O
{\displaystyle {\text{O}}}
條 じょう 光線 こうせん 介 かい 質 しつ 射 しゃ 向 むかい
Q
{\displaystyle {\text{Q}}}
方向 ほうこう [53] 根據 こんきょ 反射 はんしゃ 定律 ていりつ 當 とう 反射 はんしゃ 同 どう 入射 にゅうしゃ 會 かい 成 なり 特定 とくてい 角度 かくど 想像 そうぞう 一 いち 條 じょう 光線 こうせん
P
{\displaystyle {\text{P}}}
通過 つうか 空氣 くうき 射 しゃ 一塊 ひとかたまり 鏡 きょう 射 しゃ 中 ちゅう 塊 かたまり 鏡 きょう 上面 うわつら
O
{\displaystyle {\text{O}}}
反射 はんしゃ 定律 ていりつ 講 こう 反射 はんしゃ 線 せん
Q
{\displaystyle {\text{Q}}}
同 どう 條 じょう 法線 ほうせん [e 28] 指 ゆび 同 どう 塊 かたまり 鏡 きょう 面 めん 成 なり 垂直 すいちょく 會 かい 成 なり 角度 かくど
θ しーた
r
{\displaystyle \theta _{r}}
θ しーた
r
=
θ しーた
i
{\displaystyle \theta _{r}=\theta _{i}}
當 とう 中 なか
θ しーた
i
{\displaystyle \theta _{i}}
係 かかり
P
{\displaystyle {\text{P}}}
同 どう 法線 ほうせん 成 なり 角度 かくど 簡單 かんたん 講 こう 即 そく 係 がかり 反射 はんしゃ 角 かく 等 とう 入射 にゅうしゃ 角 かく 淨 きよし 係 がかり 已 やめ 經 けい 用 よう 同 どう 角度 かくど 等 とう 何 なん 概念 がいねん [54] [55]
附圖 ふず
附圖 ふず
喺實驗 じっけん 室 しつ 入 いれ 面 めん 展示 てんじ 反射 はんしゃ 現象 げんしょう 量 りょう 角 かく 器 き 度 ど 清楚 せいそ 顯示 けんじ 定律 ていりつ 講 こう 喺
實驗 じっけん 室 しつ 入 いれ 面 めん 展示 てんじ 反射 はんしゃ 嘅
現象 げんしょう ;
量 りょう 角 かく 器 き 嘅量
度 ど 清楚 せいそ 噉
顯示 けんじ
θ しーた
r
=
θ しーた
i
{\displaystyle \theta _{r}=\theta _{i}}
呢條
定律 ていりつ 講 こう 嘅嘢。
折 おり 射 しゃ 現 げん 折 おり 射 しゃ 涉 わたる 一 いち 條 じょう 光線 こうせん 介 かい 質 しつ 改變 かいへん 例 れい 通過 つうか 空氣 くうき 變成 へんせい 通過 つうか 玻璃 はり 前進 ぜんしん 角度 かくど 改變 かいへん 角度 かくど 會 かい 變 へん 幾多 いくた 可 か 折 おり 射 しゃ 定律 ていりつ 折 おり 射 しゃ 嘅展
現 げん ;
折 おり 射 しゃ 涉 わたる 及
一 いち 條 じょう 光線 こうせん 介 かい 質 しつ 改變 かいへん (
例 れい 如由
通過 つうか 空氣 くうき 變成 へんせい 通過 つうか 玻璃 はり )嗰陣
前進 ぜんしん 角度 かくど 改變 かいへん ,而「
角度 かくど 會 かい 變 へん 幾多 いくた 」
可 か 以用
折 おり 射 しゃ 定律 ていりつ 描述。
除 じょ 學 がく 之 の 外 そと 仲 なか 可 か 力學 りきがく 上 うえ 對 たい 郁 いく 動 どう 者 しゃ 電磁 でんじ 學 がく 上 うえ 對 たい 帶 たい 電荷 でんか 物體 ぶったい 動 どう 分析 ぶんせき 機械 きかい 工程 こうてい 等 とう 工程 こうてい 學 がく 領域 りょういき 分析 ぶんせき 機械 きかい 機 き 件 けん 郁 いく 動 どう 亦 また 都 みやこ 成 しげる 日 にち 會 かい 將 はた 件 けん 想像 そうぞう 成 なり 幾何 きか 物體 ぶったい 會 かい 件 けん 之 の 間 あいだ 距離 きょり 同 どう 角度 かくど 例 れい 子 こ 可 か 關 せき 連 れん 機構 きこう 思考 しこう [56] 亦 また 都 と 可 か 結構 けっこう 工程 こうてい 上成 うえなし 日用 にちよう 結構 けっこう 分析 ぶんせき [57] [58]
藝術 げいじゅつ 應用 おうよう [ 編輯 へんしゅう ] 耶路撒冷 嘅圓 えん 頂 いただき 清真 きよざね 寺 てら [e 29] 係 かかり 側面 そくめん 高度 こうど 同 どう 紅色 こうしょく 框 かまち 框 かまち 大 だい 上成 うえなし 黃金 おうごん 比例 ひれい 「冇咗數學 すうがく 會 かい 有 ゆう 藝術 げいじゅつ [e 30]
—盧 の 奧 おく 利 とし 包括 ほうかつ 畫 が 畫 が 雕塑 、建築 けんちく 設計 せっけい 同 どう 演算 えんざん 法 ほう 藝術 げいじゅつ 在 ざい 多門 たもん 視 み 藝 げい 都會 とかい 用 よう 到 いた 幾何 きか 學 がく 相關 そうかん 概念 がいねん 有 ゆう 學者 がくしゃ 指 ゆび 好 こう 似 に 畫 が 畫 が 視 し 藝 げい 本質 ほんしつ 上 うえ 係 がかり 間 あいだ 當 とう 中編 ちゅうへん 排 はい 顏色 かおいろ 相對 そうたい 音樂 おんがく 係 かかり 時間 じかん 當 とう 中編 ちゅうへん 排 はい 聲 こえ 必然 ひつぜん 會 かい 用 よう 到 いた 幾何 きか 學 がく 研究 けんきゅう 空間 くうかん 學 がく 考量 こうりょう [59]
黃金 おうごん 比例 ひれい [e 31]
φ ふぁい
{\displaystyle \varphi }
可 か 係 がかり 幾何 きか 學 がく 藝術 げいじゅつ 應用 おうよう 最 さい 出 だし 名 めい 子 こ 有 ゆう 藝術 げいじゅつ 工作 こうさく 者 しゃ 同 どう 學者 がくしゃ 都 と 認 みとめ 為 ため 構圖 こうず 上 うえ 展示 てんじ 某 ぼう 學 がく 特性 とくせい 藝 げい 作品 さくひん 會 かい 零 れい 舍 しゃ 有 ゆう 美感 びかん 金 きん 比例 ひれい 想像 そうぞう 有 ゆう 兩個 りゃんこ 數 すう
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
a
>
b
{\displaystyle a>b}
a
+
b
{\displaystyle a+b}
同 どう
a
{\displaystyle a}
之 これ 間 あいだ 比例 ひれい 等 とう 同 どう
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
之 これ 間 あいだ 比例 ひれい
a
{\displaystyle a}
同 どう
b
{\displaystyle b}
係 がかり 成 なり 黃金 おうごん 比例 ひれい 即 そく 係 がかり 話 ばなし [60]
a
+
b
a
=
a
b
=
def
φ ふぁい
{\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}\ {\stackrel {\text{def}}{=}}\ \varphi }
φ ふぁい =
1
+
5
2
=
1.6180339887
…
.
{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .}
有 ゆう 好 こう 多 た 藝術 げいじゅつ 工作 こうさく 者 しゃ 相 しょう 信 しんじ 文藝 ぶんげい 復興 ふっこう 時期 じき 意 い 大利 おおとし 藝術 げいじゅつ 家 か 廣 こう 將 はた 黃金 おうごん 比例 ひれい 用 よう 作品 さくひん 圖 ず 當 とう 中 なか [61] 達文 たつぶん 西 にし 作品 さくひん 蒙 こうむ 年代 ねんだい 為 ため 例 れい [62] [63]
《蒙 こうむ 全 ぜん 圖 ず
《蒙 こうむ 全 ぜん 圖 ず
蒙 こうむ 面 めん 指 ゆび 係 がかり 運用 うんよう 金 きん 長方形 ちょうほうけい 原理 げんり 蒙 こうむ 面 めん 指 ゆび 係 がかり 運用 うんよう 金 きん 長方形 ちょうほうけい 原理 げんり
除 じょ 金 きん 比例 ひれい 仲 なか 可 か 伊 い 建築 けんちく 伊 い 建築 けんちく 出 で 幾何 きか 圖案 ずあん
15 世紀 せいき 一 いち 幅 ぶく 圖畫 ずが 幅 はば 畫 が 歐 おう 洲 しゅう 同 どう 阿 おもね 拉 ひしげ 伯 はく 者 しゃ 一齊 いっせい 研究 けんきゅう 幾何 きか 學 がく 幾何 きか 學 がく 早 はや 公 おおやけ 元 もと 前 まえ 年 ねん 兩 りょう 河 かわ 流域 りゅういき 文明 ぶんめい 同 どう 古 こ 埃及 えじぷと 已 やめ 經 けい 存在 そんざい 當時 とうじ 已 やめ 經 けい 觀察 かんさつ 周圍 しゅうい 環境 かんきょう 得知 とくち 長 ちょう 度 ど 角度 かくど 同 どう 面積 めんせき 等 とう 概念 がいねん 仲 なか 概念 がいねん 測量 そくりょう 建築 けんちく 施工 しこう 同 どう 天文學 てんもんがく 等 とう 工作 こうさく 仲 なか 有 ゆう 寫 うつし 文獻 ぶんけん 記 き 低 てい 同 どう 教授 きょうじゅ 幾何 きか 學 がく 知識 ちしき 例 れい 自公 じこう 元 もと 前 まえ 年 ねん 莫斯科 か 數學 すうがく 紙 し 草書 そうしょ [e 32] 一 いち 埃及 えじぷと 紙 かみ 草 そう 文獻 ぶんけん 提供 ていきょう 方程式 ほうていしき 計 けい 物體 ぶったい 體積 たいせき [64]
古希 こき 係 かかり 幾何 きか 學 がく 一 いち 個 こ 黃金 おうごん 時期 じき 古希 こき 哲學 てつがく 家 か 畢達哥拉斯 [e 33] 公 おおやけ 元 もと 前 まえ 年 ねん 證明 しょうめい 畢氏定理 ていり ,呢條定理 ていり 到 いた 仲 なか 成 しげる 日 にち 用 よう 屬 ぞく 於幾 おき 何 なに 學 がく 基礎 きそ 之 の 一 いち 兼 けん 史上 しじょう 歷史 れきし 最 さい 悠久 ゆうきゅう 教科書 きょうかしょ 之 これ 一 いち 幾何 きか 原本 げんぽん 出 で 於大 おだい 約 やく 公 おおやけ 元 もと 前 まえ 年 ねん 書 しょ 入 いれ 面 めん 歐 おう 幾里 いくさと 得 とく 公理 こうり 等 とう 概念 がいねん 指 ゆび 係 がかり 確立 かくりつ 何 なん 學 がく 學 がく 嚴 げん [65] 除 じょ 外 がい 好 こう 出 だし 名 めい 阿 おもね 基 もと 米 まい 德 とく [e 34] 亦 また 都 と 幾何 きか 學 がく 方面 ほうめん 研究 けんきゅう 例 れい 當時 とうじ 前 まえ 所 しょ 未 み 有 ゆう 確度 かくど 計 けい 出 だし 圓周 えんしゅう 率 りつ 切 きり 數 すう [66] 同期 どうき 印度 いんど 亦 また 都 みやこ 有 ゆう 出 で 到 いた 有 ゆう 何 なん 學 がく 研究 けんきゅう [67]
中 ちゅう 世紀 せいき 伊 い 世界 せかい 有 ゆう 對 たい 幾何 きか 學 がく 作出 さくしゅつ 貢獻 こうけん 伊 い 黃金 おうごん 時期 じき 尤 ゆう 代數 だいすう 幾何 きか [68] 例 れい 子 こ 可 か 波 なみ 數學 すうがく 家 か 奧 おく 儼 げん [e 35] 對 たい 一元 いちげん 三 さん 次 じ 方 かた 程 ほど 同 どう 四邊 しへん 形 がた 研究 けんきゅう [69]
17 世紀 せいき 歐 おう 洲 しゅう 啟蒙 けいもう 時期 じき 出 で 到 いた 好 こう 多重 たじゅう 要 よう 發現 はつげん 當 とう 中 ちゅう 最 さい 出 だし 名 めい 數 すう 法 ほう 國 こく 數學 すうがく 家 か 笛 ふえ [e 36] 同 どう 埋 うめ 費 ひ 馬 ば [e 37] 發展 はってん 出 で 解析 かいせき 幾何 きか 解析 かいせき 幾何 きか 用 よう 坐 すわ 標 しるべ 分析 ぶんせき 幾何 きか 物體 ぶったい 指 ゆび 係 がかり 後 ご 微積分 びせきぶん 同 どう 精確 せいかく 物理 ぶつり 學 がく 路 ろ [70]
非 ひ 歐 おう 幾里 いくさと 得 とく 幾何 きか 頭 あたま 係 がかり 世紀 せいき 出 で 幾何 きか 理論 りろん 框 かまち 架 か 可 か 係 がかり 根本 こんぽん 改變 かいへん 人 じん 對 たい 幾何 きか 學 がく 法 ほう 挑戰 ちょうせん 當時 とうじ 多 た 根本 こんぽん 假設 かせつ 上面 うわつら 講 こう 到 いた 非 ひ 歐 おう 幾何 きか 挑戰 ちょうせん 幾里 いくさと 得 とく 幾 いく 條 じょう 個個 ここ 都 みやこ 覺 さとし 得 とく 係 がかり 公理 こうり [71]
到 いた 一 いち 世紀 せいき 初 はつ 幾何 きか 學 がく 已 やめ 經 けい 成 なり 為 ため 科學 かがく 同 どう 工程 こうてい 學 がく 工作 こうさく 當 とう 中 ちゅう 不可 ふか 或 ある 缺 かけ 知識 ちしき 包括 ほうかつ 力學 りきがく 光學 こうがく 化學 かがく 可 か 分子 ぶんし 結構 けっこう 研究 けんきゅう [72] 建築 けんちく 設計 せっけい 機械 きかい 工程 こうてい 同 どう 埋 うめ 電腦 でんのう 圖像 ずぞう 等 とう 領域 りょういき 工作 こうさく 都會 とかい 用 よう 到 いた 幾何 きか 學 がく 概念 がいねん
↑ 歐 おう 幾里 いくさと 得 とく 都 と 係 がかり 用 よう 定義 ていぎ ↑ 喺數學 がく 上 じょう 公理 こうり 係 かかり 指 ゆび 證明 しょうめい 可 か 證明 しょうめい 第 だい 頭 あたま 頭 あたま
↑ 簡化噉講,一條線嘅曲率可以由「能 のう 切 きり 線 せん 圓形 えんけい 直徑 ちょっけい 反映 はんえい 應 おう 無限 むげん 大 だい
↑ 嚴格 げんかく 想像 そうぞう 法 ほう 不 ふ 過 か 會 かい 引致 いんち 差 さ 微細 びさい 到 いた 用 よう 肉眼 にくがん 根本 こんぽん 詳 しょう 情 じょう 可 か 相對 そうたい 論 ろん 方面 ほうめん 容 よう ↑ 人 ひと 現實 げんじつ 整 せい 曲 きょく 氏 し 雪 ゆき 花 はな 好 こう 多 た 時 じ 因 いん 為 ため 人力 じんりき 物 ぶつ 力 りょく 上 じょう 制 せい 無限 むげん 重複 じゅうふく 真正 しんせい 氏 し 雪 ゆき 花 はな ↑ 對 たい 文明 ぶんめい 早期 そうき 要 よう 檢 けん 驗 けん 一 いち 把 わ 間 あいだ 尺 じゃく 可 か 條 じょう 繩 なわ 再 さい 個人 こじん 由 よし 兩邊 りょうへん 用 よう 力 りょく 拉 ひしげ 條 じょう 繩 なわ 條 じょう 繩 なわ 會 かい 成 なり 直線 ちょくせん
篇 へん 文 ぶん 用 よう 行 くだり 話 ばなし 專有 せんゆう 名詞 めいし 或 ある 者 もの 名句 めいく 英文 えいぶん 或 ある 者 もの 外語 がいご 版本 はんぽん
↑ intersection
↑ parallel
↑ foundations of geometry
↑ primitive notion
↑ axiom
↑ Euclidean geometry
↑ Elements
↑ parallel postulate
↑ volume
↑ symmetry
↑ reflection
↑ rotational symmetry
↑ congruence
↑ similarity
↑ fractal
↑ Koch snowflake
↑ ruler-and-compass construction
↑ non-Euclidean geometry
↑ spherical geometry
↑ hyperbolic geometry
↑ algebraic geometry
↑ analytic geometry
↑ differential geometry
↑ topology
↑ discrete geometry
↑ "Mathematics is the language in which God has written the universe."
↑ law of reflection
↑ normal
↑ Dome of the Rock
↑ "Without Mathematics There is No Art."
↑ golden ratio
↑ Moscow Papyrus
↑ Πυθαγόρας
↑ Ἀρχιμήδης
↑ 波 なみ 斯文 しぶん 羅 ら 馬 うま 字 じ 係 かかり ↑ René Descartes
↑ Pierre de Fermat
篇 へん 文 ぶん 引用 いんよう 下 か 文獻 ぶんけん 同 どう 網 あみ 頁 ぺーじ
↑ 1.0 1.1 Vincenzo De Risi (31 January 2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age . Birkhäuser. pp. 1–.
↑ Tabak, John (2014). Geometry: the language of space and form . Infobase Publishing. p. xiv.
↑ Staal, Frits (1999), "Greek and Vedic Geometry", Journal of Indian Philosophy , 27 (1–2): 105–127.
↑ 4.0 4.1 Martin J. Turner; Jonathan M. Blackledge; Patrick R. Andrews (1998). Fractal geometry in digital imaging . Academic Press. p. 1.
↑ Boyer, C.B. (1991) [1989]. A History of Mathematics (Second edition, revised by Uta C. Merzbach ed.). New York: Wiley. p. 43.
↑ Lamb, Evelyn (8 November 2015). "By Solving the Mysteries of Shape-Shifting Spaces, Mathematician Wins $3-Million Prize ". Scientific American .
↑ Hestenes, D. (2012). New foundations for classical mechanics (Vol. 15). Springer Science & Business Media.
↑ Marsh, D. (2006). Applied geometry for computer graphics and CAD きゃど . Springer.
↑ Guillén, M. F. (1997). Scientific management's lost aesthetic: Architecture, organization, and the Taylorized beauty of the mechanical. Administrative Science Quarterly , 682-715.
↑ Euclid's Elements - All thirteen books in one volume, Based on Heath's translation , Green Lion Press.↑ 11.0 11.1 Clark, Bowman L. (January 1985). "Individuals and Points". Notre Dame Journal of Formal Logic . 26 (1): 61-75.
↑ Coxeter, H.S.M (1969). Introduction to Geometry (2nd ed.), New York: John Wiley & Sons. p. 4.
↑ Wylie Jr., C. R. (1964), Foundations of Geometry , McGraw-Hill. pp. 92-94.
↑ Su, B. Q., & Liu, D. Z. (1989). Computational geometry: curve and surface modeling . Academic Press Professional, Inc..
↑ Szmielew, Wanda. From affine to Euclidean geometry: An axiomatic approach . Springer, (1983).
↑ Hadwiger, H., Debrunner, H., & Klee, V. (2015). Combinatorial geometry in the plane . Courier Corporation.
↑ Klee, V., & Wagon, S. (1991). Old and new unsolved problems in plane geometry and number theory (No. 11). Cambridge University Press.
↑ Henderson, David W.; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104
↑ Cajori, Florian (1926), "Origins of Fourth Dimension Concepts" , The American Mathematical Monthly , 33 (8): 397-406.
↑ Wylie Jr., C.R. (1964), Foundations of Geometry , New York: McGraw–Hill.
↑ Victor J. Katz (21 September 2000). Using History to Teach Mathematics: An International Perspective . Cambridge University Press. pp. 45-.
↑ Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry , New York: Marcel Dekker, Inc. pp. 105-8.
↑ Robin Hartshorne (11 November 2013). Geometry: Euclid and Beyond . Springer Science & Business Media. pp. 29-.
↑ Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications. In 3 vols.: vol. 1
↑ Mark de Berg; Marc van Kreveld; Mark Overmars; Otfried Schwarzkopf (2000). "Chapter 3: Polygon Triangulation". Computational Geometry (2nd revised ed.). Springer-Verlag. pp. 45-61.
↑ Symmetry . Wolfram MathWorld .↑ James, E. (2005). Symmetry and the Beautiful Universe. Journal of College Science Teaching , 34(5), 55.
↑ Derry, Gregory N. (2002). What Science Is and How It Works . Princeton University Press. pp. 269-.
↑ Borisov, Alexander; Dickinson, Mark; Hastings, Stuart (March 2010). "A Congruence Problem for Polyhedra". American Mathematical Monthly . 117 (3): 232-249.
↑ Martin, George E. (1982). "Chapter 13: Similarities in the Plane". Transformation Geometry: An Introduction to Symmetry . Springer. pp. 136-146.
↑ "Missing Square Puzzle - Diagram and Solution" . Mechamath (美國 びくに 英文 えいぶん 原著 げんちょ 歸 き . 喺2022-07-26 搵到 .↑ Koch Snowflake .↑ 33.0 33.1 Addison, Paul S. (1997). Fractals and Chaos: An Illustrated Course . Institute of Physics. p. 19.
↑ Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications", Toulouse, France - June 1992 . Atlantica Séguier Frontières. p. 25.
↑ Sala, N. (2002). Fractals in architecture: some examples. In Fractals in biology and medicine (pp. 347-358). Birkhäuser, Basel.
↑ Bovill, Carl (1996). Fractal geometry in architecture and design . Boston: Birkhauser. p. 153.
↑ 37.0 37.1 Straightedge and Compass Constructions (PDF).↑ Kazarinoff, Nicholas D. (2003) [1970]. Ruler and the Round . Mineola, N.Y.: Dover. pp. 29-30.
↑ Geometric Construction . Wolfram MathWorld .↑ What is Computer Graphics? , Cornell University Program of Computer Graphics . Last updated 04/15/98.↑ Foley, J. D., Van, F. D., Van Dam, A., Feiner, S. K., Hughes, J. F., Hughes, J., & Angel, E. (1996). Computer graphics: principles and practice (Vol. 12110). Addison-Wesley Professional.
↑ 42.0 42.1 non-Euclidean geometry . Encyclopedia Britannica .↑ Rosenfeld, B. A. (1988). A history of non-Euclidean geometry: evolution of the concept of a geometric space . New York: Springer-Verlag. p. 2.
↑ Algebraic Geometry ↑ Boyer, Carl B. (2004) [1956], History of Analytic Geometry . Dover Publications.
↑ Knudsen, Jens M.; Hjorth, Poul (2012). Elements of Newtonian Mechanics (illustrated ed.). Springer Science & Business Media. p. 30.
↑ Charleton, Walter, 1654, Physiologia Epicuro-Gassendo-Charltoniana: or a Fabrick of Science Natural Upon the Hypothesis of Atoms , London: Tho. Newcomb. Reprinted with indices and introduction by Robert Hugh Kargon, New York and London: Johnson Reprint Corporation, 1966.
↑ Ethan D. Bloch (27 June 2011). A First Course in Geometric Topology and Differential Geometry . Boston: Springer Science & Business Media.
↑ Martin D. Crossley (2011). Essential Topology . Springer Science & Business Media.
↑ Everett W. Howe; Kristin E. Lauter; Judy L. Walker (2017). Algebraic Geometry for Coding Theory and Cryptography: IPAM , Los Angeles, CA, February 2016. Springer.
↑ Bezdek, András (2003). Discrete geometry: in honor of W. Kuperberg's 60th birthday . New York, N.Y: Marcel Dekker.
↑ Pacheco Sanjuan, A. A., Mehboudi, M., Harriss, E. O., Terrones, H., & Barraza-Lopez, S. (2014). Quantitative chemistry and the discrete geometry of conformal atom-thin crystals. ACS nano , 8(2), 1136-1146.
↑ Lekner, John (1987). Theory of Reflection, of Electromagnetic and Particle Waves . Springer.
↑ Tan, R.T. (2013), Specularity, Specular Reflectance. In: Ikeuchi K. (eds) Computer Vision , Springer, Boston, MA.
↑ Young, H.D. (1992). University Physics: Extended Version With Modern Physics (8th ed.). Addison-Wesley. Ch. 35.
↑ D. Jordan and M. Steiner, "Configuration Spaces of Mechanical Linkages," Discrete and Computational Geometry , 22:297-315, 1999
↑ McKenzie, W. M. (2013). Examples in structural analysis
↑ Potts, D. M.; Zdravković, L. (1999). Finite element analysis in geotechnical engineering . Thomas Telford. ISBN 9780727727534 ↑ Goldsmith, L. T., Hetland, L., Hoyle, C., & Winner, E. (2016). Visual-spatial thinking in geometry and the visual arts. Psychology of Aesthetics , Creativity, and the Arts, 10(1), 56.
↑ Dunlap, Richard A., The Golden Ratio and Fibonacci Numbers , World Scientific Publishing, 1997.
↑ See How Artists Discover Simplicity as an Art Form in Works Which Reflect the Golden Ratio . artnet.com .↑ Da Vinci and the Divine Proportion in Art Composition . The Golden Number .↑ Livio, M. (2002). The golden ratio and aesthetics. Plus Magazine , 22.
↑ Boyer, C.B. (1991) [1989]. A History of Mathematics (2nd edition, revised by Uta C. Merzbach ed.). New York: Wiley. p. 19. "Egypt"
↑ Boyer, C.B. (1991) [1989]. A History of Mathematics (2nd edition, revised by Uta C. Merzbach ed.). New York: Wiley. p. 119. "Euclid of Alexandria"
↑ How Archimedes showed that π ぱい (PDF).↑ Hayashi, Takao (2003). "Indian Mathematics". In Grattan-Guinness, Ivor (ed.). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences . Vol. 1. Baltimore, MD: The Johns Hopkins University Press. pp. 118-130.
↑ Rāshid, Rushdī (1994). The development of Arabic mathematics : between arithmetic and algebra . Boston Studies in the Philosophy of Science. Vol. 156. p. 35.
↑ Omar Khayyam . MacTutor .↑ C.H. Edwards Jr. (2012). The Historical Development of the Calculus . Springer Science & Business Media. p. 95.
↑ Jeremy Gray (2011). Worlds Out of Nothing: A Course in the History of Geometry in the 19th Century . Springer Science & Business Media.
↑ Cotton, F. Albert; Wilkinson, Geoffrey; Murillo, Carlos A.; Bochmann, Manfred (1999), Advanced Inorganic Chemistry (6th ed.), New York: Wiley-Interscience,
Boyer, C. B. (1991) [1989]. A History of Mathematics (Second edition, revised by Uta C. Merzbach ed.). New York: Wiley. ISBN 978-0-471-54397-8 .
Bryant, J., & Sangwin, C. (2011). How round is your circle? . Princeton University Press.
Cooke, R. (2005). The History of Mathematics . New York: Wiley-Interscience. ISBN 978-0-471-44459-6 .
Hayashi, T. (2003). "Indian Mathematics". In Grattan-Guinness, Ivor (ed.). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences . Vol. 1. Baltimore, MD: The Johns Hopkins University Press. pp. 118-130. ISBN 978-0-8018-7396-6 .
Hayashi, T. (2005). "Indian Mathematics". In Flood, Gavin (ed.). The Blackwell Companion to Hinduism . Oxford: Basil Blackwell. pp. 360-375. ISBN 978-1-4051-3251-0 .
Kappraff, J. (2014). A Participatory Approach to Modern Geometry . World Scientific Publishing. doi:10.1142/8952. ISBN 978-981-4556-70-5 .
Mlodinow, L. (2002). Euclid's Window - The Story of Geometry from Parallel Lines to Hyperspace (UK ed.). Allen Lane. ISBN 978-0-7139-9634-0 .
Lobachevsky, N. I. (2010). Pangeometry. Heritage of European Mathematics Series . Vol. 4. translator and editor: A. Papadopoulos. European Mathematical Society.
主要 しゅよう 領域 りょういき 重要 じゅうよう 概念 がいねん 跟維度 分 ぶん
幾何 きか 學 がく 史 し 相關 そうかん 領域 りょういき 拉 ひしげ 雜 ざつ 相關 そうかん