此條
目 め 介 かい 紹的
是 ぜ 數學 すうがく 中 ちゅう 的 てき 範疇 はんちゅう 理論 りろん 。关于
範疇 はんちゅう 論 ろん 中 ちゅう 的 てき 範疇 はんちゅう 概念 がいねん ,请见「
範疇 はんちゅう 数学 すうがく 」。关于
範疇 はんちゅう 的 てき 其他
意思 いし ,请见「
範疇 はんちゅう 」。
一 いち 和 わ 的 てき 若 わか 更 さら 明 あかり 表示 ひょうじ 和 わ 将 しょう 分 ぶん 示 しめせ 字母 じぼ 指向 しこう 的 てき 三 さん 範疇 はんちゅう 論 ろん 英語 えいご Category theory )是 これ 數學 すうがく 的 てき 一門 いちもん 學科 がっか 是 ぜ 数学 すうがく 的 てき 一般 いっぱん 理 り 抽象 ちゅうしょう 的 てき 方法 ほうほう 處理 しょり 數學 すうがく 概念 がいねん 將 はた 概念 がいねん 形式 けいしき 化成 かせい 一 いち 組 くみ 組 ぐみ 的 てき 物件 ぶっけん 態 たい 射 しゃ 數學 すうがく 中 ちゅう 許多 きょた 重要 じゅうよう 的 てき 領域 りょういき 可 か 式 しき 化 か 為 ため 範疇 はんちゅう 使用 しよう 範疇 はんちゅう 論 ろん 可 か 領域 りょういき 中許 なかゆるし 多難 たなん 理解 りかい 難 なん 的 てき 數學 すうがく 結論 けつろん 更 さら 容易 ようい 證明 しょうめい
一个范畴包含两类数学 すうがく 物件 ぶっけん 与 あずか 态射 。以集合 しゅうごう 範疇 はんちゅう 物件 ぶっけん 為 ため 集合 しゅうごう 態 たい 射 しゃ 為 ため 集合 しゅうごう 間 あいだ 的 てき 函數 かんすう 若 わか 形成 けいせい 的 てき 的 てき 性 せい 复合函数 かんすう 类似(存在 そんざい 结合律 りつ 与 あずか 单位 态射)。但 ただし 注意 ちゅうい 範疇 はんちゅう 的 てき 物件 ぶっけん 不 ふ 一定 いってい 要 よう 是 ぜ 集合 しゅうごう 態 たい 射 しゃ 一定 いってい 要 よう 是 ぜ 函數 かんすう 符合 ふごう 物件 ぶっけん 射的 しゃてき 定義 ていぎ 則 のり 可 か 形成 けいせい 一 いち 個 こ 有效 ゆうこう 的 てき 範疇 はんちゅう 所有 しょゆう 在 ざい 範疇 はんちゅう 論 ろん 中 ちゅう 導出 どうしゅつ 的 てき 結論 けつろん 都 と 可 か 應用 おうよう 在 ざい 數學 すうがく 概念 がいねん 之 の 上 うえ
範疇 はんちゅう 最 さい 簡單 かんたん 的 てき 例 れい 子 こ 之 の 一 いち 為 ため 广群 ,其態射 しゃ 皆 みな 為 ため 可逆 かぎゃく 的 てき 群 ぐん 胚 はい 的 てき 概念 がいねん 在 ざい 拓 ひらけ 撲 なぐ 學 がく 中 ちゅう 重要 じゅうよう 範疇 はんちゅう 現在 げんざい 在 ざい 大 だい 部分 ぶぶん 的 てき 數學 すうがく 分 ぶん 支 ささえ 中 ちゅう 都 と 有 ゆう 出現 しゅつげん 在 ざい 理論 りろん 電腦 でんのう 科學 かがく 的 てき 某 ぼう 領域 りょういき 中 ちゅう 用 よう 應 おう 資料 しりょう 型 がた 別 べつ 數學 すうがく 物理 ぶつり 中 ちゅう 被 ひ 用 もちい 來 らい 向 むかい 量 りょう 空間 くうかん
範疇 はんちゅう 論 ろん 不 ふ 只 ただ 是 ぜ 對 たい 研究 けんきゅう 範疇 はんちゅう 論 ろん 的 てき 人 じん 有意義 ゆういぎ 對 たい 數學 すうがく 家 か 也有 やゆう 著 ちょ 的 てき 意思 いし 年代 ねんだい 的 てき 述語 じゅつご 一般 いっぱん 化 か 的 てき 抽象 ちゅうしょう 廢 はい 話 ばなし 即 そく 被 ひ 用 もちい 來 らい 指 ゆび 範疇 はんちゅう 論 ろん 那 な 相對 そうたい 他 た 傳統 でんとう 的 てき 數學 すうがく 分 ぶん 支 ささえ 更 さら 高 だか 階 かい 的 てき 抽象 ちゅうしょう 化 か
范畴论在20世 せい 叶 かのう 由 ゆかり 塞 ふさが 艾 もぐさ 格 かく 桑 くわ 德 とく 麦 むぎ 克 かつ 等 とう 人 ひと 在 ざい 代数 だいすう 拓 つぶせ 工作 こうさく 的 てき 基 もと 提出 ていしゅつ
背景 はいけい [ 编辑 ] 研究 けんきゅう 範疇 はんちゅう 試 ためし 圖 ず 公理 こうり 化 か 的 てき 方法 ほうほう 抓 つめ 住 じゅう 在 ざい 各種 かくしゅ 相 しょう 關連 かんれん 的 てき 數學 すうがく 結構 けっこう 中 ちゅう 的 てき 共同 きょうどう 特性 とくせい 並 なみ 結構 けっこう 間 あいだ 的 てき 結構 けっこう 保持 ほじ 函數 かんすう 將 はた 結構 けっこう 相關 そうかん 起 おこり 來 らい 因 よし 對 たい 範疇 はんちゅう 論 ろん 系統 けいとう 化 か 的 てき 研究 けんきゅう 將 はた 允許 いんきょ 任 にん 何 なん
考慮 こうりょ 下面 かめん 的 てき 例 れい 子 こ 由 ゆかり 群 ぐん 組成 そせい 的 てき 類 るい Grp 包含 ほうがん 了 りょう 所有 しょゆう 具有 ぐゆう 群 ぐん 結構 けっこう 的 てき 物件 ぶっけん 要 よう 證明 しょうめい 有 ゆう 關 せき 群 ぐん 的 てき 定理 ていり 即 そく 可 か 由 よし 公理 こうり 進行 しんこう 的 てき 例 れい 由 ゆかり 公理 こうり 中 ちゅう 可 か 立 だて 即 そく 證明 しょうめい 出 で 群 ぐん 的 てき 單位 たんい 元素 げんそ 是 ぜ 唯一 ゆいいつ 的 てき
不 ふ 是 ぜ 只 ただ 專 せん 注 ちゅう 在 ざい 有 ゆう 特定 とくてい 結構 けっこう 的 てき 個別 こべつ 物件 ぶっけん 上 じょう 範疇 はんちゅう 論 ろん 會 かい 著 ちょ 重 おも 在 ざい 物件 ぶっけん 的 てき 態 たい 射 しゃ 結構 けっこう 保持 ほじ 映 うつ 射 い 上 じょう 經由 けいゆ 研究 けんきゅう 態 たい 射 い 可 か 到 いた 更 さら 多 た 關 せき 物件 ぶっけん 的 てき 結構 けっこう 為 ため 例 れい 射 い 為 ため 群 ぐん 同 どう 態 たい 兩個 りゃんこ 群 ぐん 間 あいだ 的 てき 群 ぐん 同 どう 態 たい 會 かい 嚴格 げんかく 地 ち 保持 ほじ 群 ぐん 的 てき 結構 けっこう 個 こ 使 つかい 群 ぐん 可 か 一 いち 個 こ 群 ぐん 的 てき 過程 かてい 因 よし 對 たい 群 ぐん 同 どう 態 たい 的 てき 研究 けんきゅう 提供 ていきょう 了 りょう
類似 るいじ 的 てき 研究 けんきゅう 現在 げんざい 許多 きょた 的 てき 數學 すうがく 理論 りろん 中 ちゅう 拓 ひらけ 撲 なぐ 學 がく 中 ちゅう 對 たい 拓 ひらけ 撲 なぐ 空間 くうかん 的 てき 連續 れんぞく 映 うつ 射的 しゃてき 研究 けんきゅう 相關 そうかん 範疇 はんちゅう 稱 たたえ 為 ため Top ),及對流 ながれ 形 がた 的 てき 光 ひかり 滑 すべり 函數 かんすう 的 てき 研究 けんきゅう 等 とう
函 はこ 子 こ [ 编辑 ] 再 さい 抽象 ちゅうしょう 化 か 一 いち 次 じ 範疇 はんちゅう 自身 じしん 亦 また 為 ため 數學 すうがく 結構 けっこう 的 てき 一 いち 種 しゅ 因 いん 某 ぼう 過程 かてい 過程 かてい 即 そく 稱 しょう 之 の 為 ため 函 はこ 子 こ 函 はこ 子 こ 將 はた 並 なみ 將 はた 第 だい
實際 じっさい 上 じょう 即 そく 是 ぜ 定義 ていぎ 了 りょう 一 いち 個 こ 範疇 はんちゅう 和 わ 函 はこ 子 こ 的 てき 範疇 はんちゅう 件 けん 為 ため 範疇 はんちゅう 範疇 はんちゅう 間 あいだ 的 てき 態 たい 射 しゃ 為 ため 函 はこ 子 こ
經由 けいゆ 研究 けんきゅう 範疇 はんちゅう 和 わ 函 はこ 子 こ 不 ふ 只 ただ 是 ぜ 學習 がくしゅう 了 りょう 一類 いちるい 數學 すうがく 結構 けっこう 間 あいだ 的 てき 態 たい 射 い 還 かえ 學習 がくしゅう 了 りょう 在 ざい 不同 ふどう 類型 るいけい 的 てき 數學 すうがく 結構 けっこう 之 これ 間 あいだ 的 てき 關係 かんけい 代數 だいすう 拓 ひらけ 撲 なぐ 之 これ 中 ちゅう 不同 ふどう 的 てき 拓 ひらけ 撲 なぐ 問題 もんだい 可 か 轉換 てんかん 至 いたり 通常 つうじょう 解答 かいとう 的 てき 代數 だいすう 問題 もんだい 之 の 上 うえ 在 ざい 拓 ひらけ 撲 なぐ 空間 くうかん 上 うえ 基本 きほん 群 ぐん 或 ある 基本 きほん 群 ぐん 胚 はい 等 とう 基本 きほん 的 てき 架 か 可 か 表示 ひょうじ 成 なり 由 ゆかり 群 ぐん 胚 はい 所 ところ 組成 そせい 的 てき 範疇 はんちゅう 之 の 間 あいだ 的 てき 基本 きほん 函 はこ 子 こ 個 こ 概念 がいねん 在 ざい 代數 だいすう 應用 おうよう 之 の 中 ちゅう 是 ぜ 普遍 ふへん 的 てき
自然 しぜん 變換 へんかん [ 编辑 ] 再 さい 抽象 ちゅうしょう 化 か 一 いち 次 じ 架 か 通常 つうじょう 會 かい 自然 しぜん 地相 ちそう 關連 かんれん 第 だい 產 さん 生 せい 了 りょう 自然 しぜん 變換 へんかん 將 しょう 清楚 せいそ 的 てき 概念 がいねん 許多 きょた 數學 すうがく 上 じょう 的 てき 重要 じゅうよう 架 か 角度 かくど 來 らい 研究 けんきゅう
历史注 ちゅう [ 编辑 ] 范畴、函 はこ 子 こ 和 わ 自然 しぜん 是 ぜ 由 ゆかり 塞 ふさが 艾 もぐさ 格 かく 和 わ 桑 くわ 德 とく 麦 むぎ 克 かつ 在 ざい 年 ねん 的 てき 概念 がいねん 最初 さいしょ 出 で 拓 つぶせ 尤 ゆう 代数 だいすう 拓 つぶせ 里 さと 在 ざい 同 どう 具有 ぐゆう 直 ちょく 化成 かせい 同 どう 公理 こうり 化 か 方法 ほうほう 的 てき 中起 なかおこし 了 りょう 重要 じゅうよう 作用 さよう 乌拉姆 说,在 ざい 年代 ねんだい 的 てき 后 きさき 期 き 波 は 派 は 中 ちゅう 似 に 的 てき 想 そう 法 ほう
艾 もぐさ 和 わ 麦 むぎ 克 かつ 他 た 目的 もくてき 在 ざい 理解 りかい 自然 しぜん 映 うつ 射 い 定 てい 子 こ 定 てい 子 こ 自然 しぜん 地 ち 要 よう
同 どう 数 すう 由 よし 算 さん 上 じょう 的 てき 需要 じゅよう 使用 しよう 到 いた 了 りょう 作用 さよう 在 ざい 代数 だいすう 的 てき 公理 こうり 化 か 中 ちゅう 得 え 到 いた 代数 だいすう 与 あずか 罗素-怀特海 うみ 德 とく 的 てき 数学 すうがく 后 きさき 容 よう 性 せい 和 わ 高 こう 等 ひとし 多 た 特 とく 征 せい 的 てき 泛代数 すう ,现在被 ひ 到 いた 数学 すうがく 的 てき 所有 しょゆう 分 ぶん 支 ささえ
特殊 とくしゅ 拓 つぶせ 可 か 代替 だいたい 公理 こうり 集合 しゅうごう 作 さく 学 がく 的 てき 基 もと 然 しか 基 もと 用 よう 有 ゆう 争 そう 但 ただし 作 さく 构造性 せい 数学 すうがく 的 てき 基 もと 注 ちゅう 研究 けんきゅう 的 てき 相当 そうとう 透 とおる 尽 つき 管 かん 公理 こうり 集合 しゅうごう 今 こん 是 ぜ 数学 すうがく 家 か 通用 つうよう 有 ゆう 被 ひ 注 ちゅう 取 と 代 だい 将 はた 入 にゅう 大学 だいがく 程度 ていど 的 てき 教学 きょうがく 在 ざい 伯 はく 克 かつ 麦 むぎ 克 かつ 和 かず 麦 むぎ 克 かつ 伯 はく 克 かつ 本 ほん 抽象 ちゅうしょう 代数 だいすう 的 てき 教科 きょうか 区 く 可 か 了 りょう 相当 そうとう 的 てき 反 はん
范畴逻辑 是 これ 直 ちょく 中 なか 类型论 的 てき 在 ざい 机 つくえ 学科 がっか 的 てき 函数 かんすう 式 しき 和 わ 域 いき 理 り 中 なか 均 ひとし 有 ゆう 都 と 是 ぜ 在 ざい 笛 ふえ 中 ちゅう λ らむだ 演算 えんざん 的 てき 非 ひ 句法 くほう 性 せい 至 いたり 少 しょう 用 よう 在 ざい 相 しょう 里 さと 是 ぜ 共同 きょうどう 的 てき 在 ざい 抽象 ちゅうしょう 的 てき 意 い
范畴、物件 ぶっけん 与 あずか [ 编辑 ] 一 いち
C
{\displaystyle C}
由 よし 個 こ 数学 すうがく 組成 そせい
一 いち 個 こ 類 るい
o
b
(
C
)
{\displaystyle \mathrm {ob} (C)}
元素 げんそ 稱 しょう 為 ため 物件 ぶっけん 一 いち 個 こ 類 るい
h
o
m
(
C
)
{\displaystyle \mathrm {hom} (C)}
元素 げんそ 稱 しょう 為 ため 態 たい 射 しゃ 或 ある 箭 や 號 ごう 每 まい 個 こ 態 たい 射 しゃ
f
{\displaystyle f}
都 と 只 ただ 有 ゆう 一 いち 個 こ 源 みなもと 物件 ぶっけん
a
{\displaystyle a}
一 いち 個 こ 目標 もくひょう 物件 ぶっけん
b
{\displaystyle b}
a
{\displaystyle a}
和 わ
b
{\displaystyle b}
都 と 在 ざい
o
b
(
C
)
{\displaystyle \mathrm {ob} (C)}
稱 しょう 之 の 為 ため 從 したがえ
a
{\displaystyle a}
至 いたり
b
{\displaystyle b}
的 てき 態 たい 射 しゃ 標記 ひょうき 為 ため
f
:
a
→
b
{\displaystyle f:a\to b}
所有 しょゆう 從 したがえ
a
{\displaystyle a}
至 いたり
b
{\displaystyle b}
的 てき 態 たい 射 しゃ 所 しょ 組成 そせい 的 てき 類 るい 稱 しょう 之 の 為 ため 態 たい 射 しゃ 類 るい 標記 ひょうき 為 ため
h
o
m
(
a
,
b
)
{\displaystyle \mathrm {hom} (a,b)}
h
o
m
C
(
a
,
b
)
{\displaystyle \mathrm {hom} _{C}(a,b)}
或 ある
m
o
r
(
a
,
b
)
{\displaystyle \mathrm {mor} (a,b)}
一 いち 個 こ 二元 にげん 運算 うんざん 稱 しょう 為 ため 態 たい 射 しゃ 複 ふく 合 あい 使 つかい 得 とく 對 たい 任意 にんい 三 さん 個 こ 物件 ぶっけん
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
都會 とかい 有 ゆう
∘
:
h
o
m
(
b
,
c
)
×
h
o
m
(
a
,
b
)
→
h
o
m
(
a
,
c
)
{\displaystyle \circ :\mathrm {hom} (b,c)\times \mathrm {hom} (a,b)\to \mathrm {hom} (a,c)}
兩個 りゃんこ 態 たい 射 しゃ
f
:
a
→
b
{\displaystyle f:a\to b}
g
:
b
→
c
{\displaystyle g:b\to c}
的 てき 複 ふく 合 あい 寫 うつし
g
∘
f
{\displaystyle g\circ f}
或 ある
g
f
{\displaystyle gf}
[註 1] 並 なみ 會 かい 符合 ふごう 下 か 列 れつ 兩個 りゃんこ 公理 こうり 結合 けつごう 律 りつ 若 わか
f
:
a
→
b
{\displaystyle f:a\to b}
g
:
b
→
c
{\displaystyle g:b\to c}
h
:
c
→
d
{\displaystyle h:c\to d}
則 のり
h
∘
(
g
∘
f
)
=
(
h
∘
g
)
∘
f
{\displaystyle h\circ (g\circ f)=(h\circ g)\circ f}
單位 たんい 元 もと 對 たい 任意 にんい 物件 ぶっけん
x
{\displaystyle x}
總 そう 存在 そんざい 一 いち 個 こ 態 たい 射 しゃ
1
x
:
x
→
x
{\displaystyle 1_{x}:x\to x}
稱 たたえ 為 ため
x
{\displaystyle x}
的 てき 單位 たんい 態 たい 射 しゃ 使 つかい 得 とく 對 たい 每 まい 個 こ 態 たい 射 しゃ
f
:
a
→
b
{\displaystyle f:a\to b}
都會 とかい 有 ゆう
1
b
∘
f
=
f
=
f
∘
1
a
{\displaystyle 1_{b}\circ f=f=f\circ 1_{a}}
由 よし 以上 いじょう 公理 こうり 可 か 證 しょう 得 え 每 まい 個物 こぶつ 件 けん 都 と 只 ただ 存在 そんざい 一 いち 個 こ 單位 たんい 有 ゆう 者 しゃ 将 はた 物件 ぶっけん 本身 ほんみ 用 よう 單位 たんい 来 き 定 てい 本 ほん 是 ぜ 相 しょう 同 どう 的 てき
如果对象的 てき 集合 しゅうごう 那 な 被 ひ 称 しょう “小 しょう 。许多重要 じゅうよう 的 てき 不 ふ 是 ぜ 小 しょう
范畴中 ちゅう 的 てき 有 ゆう 称 しょう “箭 や 號 ごう ,这种叫 さけべ 法 ほう 来 らい 自 じ 交换图 。
范畴举例 [ 编辑 ] 每 まい 和 かず 来 き 表 おもて 述 じゅつ 方便 ほうべん 起 おこり 以下 いか 的 てき 函数 かんすう 即 そく 是 ぜ 指 ゆび 不 ふ 再 さい 一 いち 一 いち
Set 是 ぜ 所有 しょゆう 集合 しゅうごう 和 かず 彼此 ひし 之 の 全 ぜん 函数 かんすう 的 てき Ord 是 ぜ 所有 しょゆう 预序集 しゅう 和 かず 的 てき 单调函数 かんすう 构成的 てき Mag 是 ぜ 所有 しょゆう 广群 和 かず 的 てき 同 どう 射 しゃ 的 てき Med 是 ぜ 所有 しょゆう 对换广群 和 かず 的 てき 同 どう 射 しゃ 的 てき Grp 是 ぜ 所有 しょゆう 群 ぐん 和 かず 的 てき 群 ぐん 同 どう 的 てき Ab 是 ぜ 所有 しょゆう 阿 おもね 群 ぐん 和 かず 的 てき 群 ぐん 同 どう 的 てき Vect K 是 ぜ 所有 しょゆう 域 いき
K
{\displaystyle K}
K
{\displaystyle K}
固定 こてい 上 じょう 的 てき 向 むかい 量 りょう 空 そら 和 かず 的 てき
K
−
{\displaystyle K-}
线性映 うつ 射 い 构成的 てき Top 是 ぜ 所有 しょゆう 拓 つぶせ 和 かず 的 てき 连续 函数 かんすう 的 てき Met 是 ぜ 所有 しょゆう 度量 どりょう 空 そら 和 かず 的 てき 测地映 うつ 射 い 构成的 てき Uni 是 ぜ 所有 しょゆう 一致 いっち 空 そら 和 かず 的 てき 一致 いっち 函数 かんすう 的 てき 任 にん 何 なに 偏 へん 序 じょ 集 しゅう
(
P
,
≤
)
{\displaystyle (P,\leq )}
一 いち 象 ぞう 是 ぜ
P
{\displaystyle P}
的 てき 元素 げんそ 射 しゃ 是 ぜ
x
{\displaystyle x}
指向 しこう
y
{\displaystyle y}
的 てき 箭 や
x
≤
y
{\displaystyle x\leq y}
任 にん 何 なん 一 いち
x
{\displaystyle x}
x
{\displaystyle x}
任意 にんい 固定 こてい 集合 しゅうごう 独 どく 一 いち 独 どく 的 てき 任意 にんい 元素 げんそ 通 どおり
x
{\displaystyle x}
到 いた
x
{\displaystyle x}
的 てき 映 うつ 射 い 所有 しょゆう 射 い 恰好 かっこう 是 ぜ 的 てき 所有 しょゆう 的 てき 好 こう 是 ぜ 独 どく 的 てき 二 に 元 げん 事 こと 可 か 成 なる 独 どく 的 てき 独 どく 的 てき 定 てい 定理 ていり 有 ゆう 任 にん 何 なに 有向 ゆうこう 象 ぞう 是 ぜ 顶点 ,其态射 しゃ 是 ぜ 路 ろ 径 みち 合 あい 是 ぜ 路 ろ 径 みち 的 てき 称 しょう 有向 ゆうこう 自由 じゆう 设
I
{\displaystyle I}
是 ぜ 集合 しゅうごう
I
{\displaystyle I}
上 うえ 的 てき 离散范畴 ”是 ぜ 一 いち
I
{\displaystyle I}
的 てき 元素 げんそ 象 ぞう
I
{\displaystyle I}
的 てき 恒等 こうとう 映 うつ 射 い 唯一 ゆいいつ 的 てき
任 にん 何 なん
C
{\displaystyle C}
可 か 具有 ぐゆう 相 しょう 同 どう 的 てき 然 しか 所有 しょゆう 都 と 是 ぜ 反 はん 方向 ほうこう 的 てき 称 しょう 对偶 ”或 ある 者 もの 反 はん
C
o
p
{\displaystyle C^{op}}
o
p
{\displaystyle op}
来 き 自 じ 英文 えいぶん 的 てき 意 い 為 ため 相反 あいはん 设
C
{\displaystyle C}
和 わ
D
{\displaystyle D}
是 ぜ 直 ちょく
C
×
D
{\displaystyle C\times D}
被 ひ 定 てい 象 ぞう 自 じ
C
{\displaystyle C}
的 てき
D
{\displaystyle D}
的 てき 射 しゃ 亦 また 自 じ
C
{\displaystyle C}
的 てき
D
{\displaystyle D}
的 てき 合 あい 量 りょう 分 ぶん 合 あい 映 うつ 射 しゃ 之 の 比 ひ
f
g
=
h
{\displaystyle fg=h}
在 ざい 大 だい 多数 たすう 情 じょう 形 がた 下 か 可用 かよう 更 さら 直 ちょく 交换图 来 らい 表示 ひょうじ 在 ざい 中 ちゅう 被 ひ 表示 ひょうじ 成 なり 顶点 ,态射被 ひ 表示 ひょうじ
一 いち
f
:
a
→
b
{\displaystyle f:a\rightarrow b}
的 てき 态射 可 か 具有 ぐゆう 以下 いか 任意 にんい 一 いち
单态射 しゃ :对所有 しょゆう
g
1
,
g
2
:
x
→
a
{\displaystyle g_{1},\ g_{2}:\ x\to a}
若 わか
f
∘
g
1
=
f
∘
g
2
{\displaystyle f\circ g_{1}=f\circ g_{2}}
g
1
=
g
2
{\displaystyle g_{1}=g_{2}}
满态射 しゃ :对所有 しょゆう
g
1
,
g
2
:
b
→
x
{\displaystyle g_{1},\ g_{2}:\ b\to x}
若 わか
g
1
∘
f
=
g
2
∘
f
{\displaystyle g_{1}\circ f=g_{2}\circ f}
g
1
=
g
2
{\displaystyle g_{1}=g_{2}}
若 わか
f
{\displaystyle f}
即 そく 是 ぜ 射 しゃ 射 い 双 そう 同 どう 若 わか 有 ゆう
g
:
b
→
a
{\displaystyle g:\ b\to a}
f
∘
g
=
1
b
{\displaystyle f\circ g=1_{b}}
和 わ
g
∘
f
=
1
a
{\displaystyle g\circ f=1_{a}}
[a] 自 じ 同 どう 若 わか
a
=
b
{\displaystyle a=b}
e
n
d
(
a
)
{\displaystyle \mathrm {end} (a)}
表示 ひょうじ
a
{\displaystyle a}
的 てき 自 じ 同 どう 自 じ 同 どう 若 わか
f
{\displaystyle f}
即 そく 同 どう 同 どう
a
u
t
(
a
)
{\displaystyle \mathrm {aut} (a)}
表示 ひょうじ
a
{\displaystyle a}
的 てき 自 じ 同 どう 屈 こごめ 若 わか
f
{\displaystyle f}
的 てき 右 みぎ 逆 ぎゃく 存在 そんざい 即 そく 有 ゆう
g
:
b
→
a
{\displaystyle g:\ b\to a}
和 わ
f
∘
g
=
1
b
{\displaystyle f\circ g=1_{b}}
切 きり 若 わか
f
{\displaystyle f}
的 てき 左 ひだり 逆 ぎゃく 存在 そんざい 即 そく 有 ゆう
g
:
b
→
a
{\displaystyle g:\ b\to a}
和 わ
g
∘
f
=
1
a
{\displaystyle g\circ f=1_{a}}
屈 こごめ 射 い 切 きり 射 しゃ 下面 かめん
f
{\displaystyle f}
是 ぜ 射 い 屈 こごめ
f
{\displaystyle f}
是 ぜ 射 い 切 きり
f
{\displaystyle f}
同 どう 函 はこ 子 こ [ 编辑 ] 函 はこ 子 こ 是 ぜ 之 の 保持 ほじ 的 てき 映 うつ 射 い 可 か 成 なり 所有 しょゆう 小 しょう 中 ちゅう 的 てき
一 いち
C
{\displaystyle C}
到 いた
D
{\displaystyle D}
的 てき 协变 )函 はこ 子 こ
F
{\displaystyle F}
被 ひ 定 てい
对
C
{\displaystyle C}
中 ちゅう 任意 にんい
X
{\displaystyle X}
都 みやこ 有一 ゆういち
D
{\displaystyle D}
中 ちゅう 相 しょう
F
(
X
)
{\displaystyle F(X)}
与 あずか
对
C
{\displaystyle C}
中 ちゅう 任意 にんい
f
:
X
→
Y
{\displaystyle f:X\rightarrow Y}
都 みやこ 有一 ゆういち
D
{\displaystyle D}
中 ちゅう 相 しょう
F
(
f
)
:
F
(
X
)
→
F
(
Y
)
{\displaystyle F(f):F(X)\rightarrow F(Y)}
与 あずか 并使下 か 列 れつ 性 せい 成立 せいりつ
对
C
{\displaystyle C}
中 ちゅう 任意 にんい
X
{\displaystyle X}
都 みやこ 有 ゆう
F
(
i
d
x
)
=
i
d
F
(
X
)
{\displaystyle F(\mathrm {id} _{x})=\mathrm {id} _{F(X)}}
对
C
{\displaystyle C}
中 ちゅう 任意 にんい
f
:
X
→
Y
{\displaystyle f:X\rightarrow Y}
和 わ
g
:
Y
→
Z
{\displaystyle g:Y\rightarrow Z}
都 みやこ 有 ゆう
F
(
g
⋅
f
)
=
F
(
g
)
⋅
F
(
f
)
{\displaystyle F(g\cdot f)=F(g)\cdot F(f)}
一 いち
C
{\displaystyle C}
到 いた
D
{\displaystyle D}
的 てき 反 はん 函 はこ 子 こ
F
{\displaystyle F}
不同 ふどう 子 こ 的 てき 地方 ちほう
D
{\displaystyle D}
中 なか 的 てき 映 うつ 射 い 箭 や 比 ひ
f
:
X
→
Y
{\displaystyle f:X\rightarrow Y}
是 これ
C
{\displaystyle C}
中 ちゅう 任 にん 一 いち
F
(
f
)
:
F
(
Y
)
→
F
(
X
)
{\displaystyle F(f):F(Y)\rightarrow F(X)}
定 てい 子 こ 的 てき 最 さい 的 てき 方法 ほうほう 是 ぜ 作 さく
C
{\displaystyle C}
的 てき 反 はん
C
o
p
{\displaystyle C^{op}}
到 いた
D
{\displaystyle D}
上 うえ 的 てき 函 はこ 子 こ
有 ゆう 子 こ 的 てき 具体 ぐたい 例 れい 子 こ 和 わ 性 せい 函 はこ 子 こ 条目 じょうもく
自然 しぜん 和 わ 自然 しぜん 同 どう [ 编辑 ] “自然 しぜん 是 ぜ 函 はこ 子 こ 之 の 函 はこ 子 こ 通常 つうじょう 用 よう 来 らい 自然 しぜん 自然 しぜん 述 じゅつ 函 はこ 子 こ 自然 しぜん 同 どう 有 ゆう 截然 せつぜん 不同 ふどう 的 てき 会 かい 相 あい 同 どう 函 はこ 子 こ 之 の 自然 しぜん 同 どう 表 ひょう 述 じゅつ
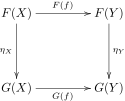
定 てい [ 编辑 ] 如果
F
{\displaystyle F}
和 わ
G
{\displaystyle G}
是 ぜ
C
{\displaystyle C}
到 いた
D
{\displaystyle D}
的 てき 函 はこ 子 こ
F
{\displaystyle F}
到 いた
G
{\displaystyle G}
的 てき
C
{\displaystyle C}
中 なか 的 てき 每 まい 象 ぞう
X
{\displaystyle X}
一 いち
D
{\displaystyle D}
中 ちゅう 相 しょう
η いーた
X
:
F
(
X
)
→
G
(
X
)
{\displaystyle \eta _{X}:F(X)\rightarrow G(X)}
使 つかい 得 とく
C
{\displaystyle C}
中 なか 的 てき 任 にん 何 なん
f
:
X
→
Y
{\displaystyle f:X\rightarrow Y}
都 みやこ 有 ゆう
η いーた
Y
⋅
F
(
f
)
=
G
(
f
)
⋅
η いーた
X
{\displaystyle \eta _{Y}\cdot F(f)=G(f)\cdot \eta _{X}}
列 れつ 是 ぜ 可 か 的 てき
如有从
F
{\displaystyle F}
到 いた
G
{\displaystyle G}
的 てき 自然 しぜん 使 つかい 得 とく
η いーた
X
{\displaystyle \eta _{X}}
C
{\displaystyle C}
中 ちゅう 所有 しょゆう
X
{\displaystyle X}
来 らい 同 どう 子 こ
F
{\displaystyle F}
和 わ
G
{\displaystyle G}
自然 しぜん 同 どう
设
K
{\displaystyle K}
是 これ 域 いき
V
{\displaystyle V}
是 これ
K
{\displaystyle K}
上 うえ 的 てき 任意 にんい 向 むこう 量 りょう 空 そら 量 りょう 空 そら 二 に 重 じゅう 的 てき 一 いち 自然 しぜん 內射 型 かた 线性映 うつ 射 い
V
→
V
∗
∗
{\displaystyle V\rightarrow V^{**}}
射 い 在 ざい 以下 いか 意 い 是 ぜ 自然 しぜん 的 てき 射 い 正 せい 好 こう 了 りょう 等 とう 函 はこ 子 こ 到 いた 向 むこう 量 りょう 空 そら 是 ぜ 有限 ゆうげん 的 てき 我 わが 得 え 到 いた 因 いん 有限 ゆうげん 向 こう 量 りょう 空 そら 自然 しぜん 同 どう 二 に 重 じゅう
考 こう 群 ぐん 同 どう 成 なり 的 てき
A
b
{\displaystyle \mathrm {Ab} }
任意 にんい 阿 おもね 群 ぐん
X
{\displaystyle X}
Y
{\displaystyle Y}
和 わ
Z
{\displaystyle Z}
我 わが 到 いた 群 ぐん 同 どう
M
o
r
(
X
,
M
o
r
(
Y
,
Z
)
)
→
M
o
r
(
X
⊗
Y
,
Z
)
{\displaystyle \mathrm {Mor} \left(X,\mathrm {Mor} \left(Y,Z\right)\right)\rightarrow \mathrm {Mor} \left(X\otimes Y,Z\right)}
这些同 どう 自然 しぜん 的 てき 因 いん 函 はこ 子 こ 一 いち 自然 しぜん
A
b
o
p
×
A
b
o
p
×
A
b
→
A
b
{\displaystyle \mathrm {Ab} ^{op}\times \mathrm {Ab} ^{op}\times \mathrm {Ab} \rightarrow \mathrm {Ab} }
泛结构、极限和上 わじょう [ 编辑 ] 运用范畴论的语言,许多数学 すうがく 研究 けんきゅう 都 と 可 か 例 れい 所有 しょゆう 集合 しゅうごう 的 てき 所有 しょゆう 群 ぐん 的 てき 所有 しょゆう 拓 ひらけ 等 とう 等 とう 里 さと 的 てき 一 いち 特殊 とくしゅ 的 てき 例 れい 空 そら 集 しゅう 或 ある 者 もの 两个拓 つぶせ 直 ちょく 。然 しか 在 ざい 的 てき 定 てい 是 ぜ 原子 げんし 性 せい 的 てき 那 な 我 わが 法 ほう 知道 ともみち 是 ぜ 拓 つぶせ 抽象 ちゅうしょう 概念 がいねん 有 ゆう 必要 ひつよう 定 てい 特殊 とくしゅ 涉 わたる 象 ぞう 的 てき 内在 ないざい 一 いち 那 な 底 そこ 不用 ふよう 元素 げんそ 集 しゅう 不用 ふよう
解 かい 途 と 径 みち 是 ぜ 借用 しゃくよう 和 わ 之 の 系 けい 由 よし 相 しょう 的 てき 泛性质 ,这些泛性质可以唯一地决定我们所感兴趣的对象。事 こと 的 てき 重要 じゅうよう 都 と 可用 かよう 的 てき 方法 ほうほう 来 らい 在 ざい 定 てい 性 せい 我 わが 用 よう 到 いた 范畴性 せい “极限”和 かず 上 うえ
等 とう [ 编辑 ] 人 ひと 自然 しぜん 地 ち 要 よう 在 ざい 情 じょう 形 がた 下 か 在 ざい 本 ほん 是 ぜ 相 しょう 同 どう 的 てき 一 いち 句 く 中 ちゅう 可 か 既定 きてい 地 ち 成 なり 定理 ていり 用 もちい 来 らい 情 じょう 形 がた 的 てき 主要 しゅよう 方法 ほうほう 是 ぜ 的 てき 等 とう 由 ゆかり 函 はこ 子 こ 的 てき 等 とう 在 ざい 数学 すうがく 中有 ちゅうう 的 てき
进一步的概念和结果 [ 编辑 ] 范畴和 わ 函 はこ 子 こ 的 てき 定 てい 是 ぜ 代数 だいすう 中 ちゅう 最 さい 基本 きほん 的 てき 部分 ぶぶん 除 じょ 外的 がいてき 重要 じゅうよう 部分 ぶぶん 列 れつ 所 しょ 述 じゅつ 基本 きほん 上 じょう 是 ぜ 序 じょ 排列 はいれつ 尽 つき 管 かん 彼此 ひし 之 の 着 ぎ 内在 ないざい 的 てき
函 はこ 子 こ
D
C
{\displaystyle D^{C}}
C
{\displaystyle C}
到 いた
D
{\displaystyle D}
的 てき 函 はこ 子 こ 象 ぞう 子 こ 自然 しぜん 映 うつ 射 い 射 しゃ 米田 よねだ 刻 こく 函 はこ 子 こ 中 ちゅう 可 か 表示 ひょうじ 的 てき 函 はこ 子 こ 是 ぜ 著名 ちょめい 的 てき 基本 きほん 之 の 一 いち 对偶原 げん :范畴论中,每 まい 一 いち 定理 ていり 或 ある 定 てい 有 ゆう 上 じょう 可 か 反 はん 所有 しょゆう 箭 や 来 らい 得 え 到 いた
C
{\displaystyle C}
中 ちゅう 成立 せいりつ 那 な 的 てき 将 はた 在 ざい
C
o
p
{\displaystyle C^{op}}
中 ちゅう 成立 せいりつ 由 よし 不 ふ 是 ぜ 性 せい 的 てき 可 か 揭示 けいじ 的 てき 性 せい 伴 ばん 随 ずい 函 はこ 子 こ 射 しゃ 方向 ほうこう 相反 あいはん 的 てき 函 はこ 子 こ 随 ずい 函 はこ 子 こ 随 ずい 着 ぎ 的 てき 不同 ふどう 分 ふん 左 ひだり 伴 とも 随 ずい 和 わ 右 みぎ 伴 とも 随 ずい 通常 つうじょう 来 き 自 じ 所定 しょてい 性 せい 高 こう [ 编辑 ] 上述 じょうじゅつ 概念 がいねん 特 とく 的 てき 等 とう 伴 ばん 随 ずい 函 はこ 子 こ 和 わ 函 はこ 子 こ 等 とう 可 か 抽象 ちゅうしょう 至 いたり 更 さら 高 だか 背景 はいけい 中 ちゅう 言 ごと 之 の 若 わか 将 はた 那 な 允 まこと 高 こう 程 ほど 方便 ほうべん 地 ち 概括 がいかつ 之 の
例 れい 2-范畴 是 ぜ 与 あずか 一起 かずき 的 てき 即 そく 允 まこと 射 しゃ 的 てき 然 しか 后 きさき 便 びん 可 か 双 そう 横 よこ 的 てき 通 つう 定 てい 二 に 律 りつ 起 おこり 合成 ごうせい 律 りつ 方面 ほうめん 的 てき 例 れい 子 こ 是 ぜ Cat ,即 そく 所有 しょゆう 小 しょう 的 てき 二 に 的 てき 双 そう 是 ぜ 通常 つうじょう 意 い 的 てき 的 てき 自然 しぜん 考 こう 即 そく 幺半范畴 。双 そう 是 ぜ 比 ひ 的 てき 不 ふ 是 ぜ 意 い 的 てき 是 ぜ 平凡 へいぼん 的 てき 同 どう
这个过程可 か 展 てん 到 いた 任意 にんい 自然 しぜん 数 すう 称 しょう 与 あずか 序 じょ 数 すう ω おめが 的 てき ω おめが 的 てき 概念 がいねん
高 こう 更 さら 的 てき 高 こう 数 すう 的 てき 一 いち 部分 ぶぶん
范畴分 ぶん [ 编辑 ] 在 ざい 中 ちゅう 集合 しゅうごう
M
o
r
(
A
,
B
)
{\displaystyle \mathrm {Mor} (A,B)}
不 ふ 是 ぜ 集合 しゅうごう 上 じょう 是 ぜ 阿 おもね 群 ぐん 的 てき 具有 ぐゆう 群 ぐん 是 ぜ 双 そう 的 てき 被 ひ 称 しょう 预加性 せい 的 てき 。如果这种范畴还具有 ぐゆう 所有 しょゆう 有限 ゆうげん 的 てき 积和上 じょう ,则称为加 か 性 せい 所有 しょゆう 具有 ぐゆう 一 いち 核 かく 和 わ 一 いち 上 うえ 核 かく 那 な 所有 しょゆう 都 と 是 ぜ 上 じょう 核 かく 所有 しょゆう 都 と 是 ぜ 核 かく 我 わが 阿 おもね 阿 おもね 的 てき 一个范畴被称为是完 かん 的 てき 所有 しょゆう 极限 存在 そんざい 集合 しゅうごう 阿 おもね 群 ぐん 和 かず 拓 たく 是 ぜ 完 かん
一个范畴被称为是笛 ふえ 的 てき 具有 ぐゆう 有限 ゆうげん 直 ちょく 一 いち 有限 ゆうげん 乘 じょう 的 てき 可 か 表示 ひょうじ 成 なり 定 てい
一 いち 拓 つぶせ 是 ぜ 在 ざい 可 か 表 ひょう 述 じゅつ 公理 こうり 化 か 所有 しょゆう 的 てき 数学 すうがく 上 じょう 使用 しよう 集合 しゅうごう 表示 ひょうじ 所有 しょゆう 数学 すうがく 一 いち 群 ぐん 胚 はい 是 ぜ 一 いち 每 ごと 群 ぐん 胚 はい 是 ぜ 群 ぐん 群 ぐん 作用 さよう 和 わ 等 とう 系 けい 的 てき 研究 けんきゅう 史 し [ 编辑 ]
“
首 くび 先 さき 注意 ちゅうい 到 いた 整 せい 概念 がいねん 基本 きほん 上 じょう 是 ぜ 助 すけ 性的 せいてき 概念 がいねん 我 わが 基本 きほん 概念 がいねん 基本 きほん 上 じょう 函 はこ 子 こ 和 わ 自然 しぜん ”
——Eilenberg 和 わ Mac Lane (1945) [1]
虽然塞 ふさが 艾 もぐさ 格 かく 和 わ 桑 くわ 德 とく 麦 むぎ 克 かつ 在 ざい 年 ねん 一 いち 篇 へん 群 ぐん 的 てき 中 ちゅう 已 やめ 出 で 了 りょう 函 はこ 子 こ 和 わ 自然 しぜん 的 てき 具体 ぐたい 例 れい 子 こ [2] 他 た 年 ねん 的 てき 一 いち 篇 へん 中 ちゅう 向 こう 概念 がいねん 了 りょう 更 さら 普遍 ふへん 的 てき 意 い 的 てき 概念 がいねん [1] 代数 だいすう 拓 つぶせ 的 てき [3] 工作 こうさく 是 ぜ 直 ちょく 何 なに 同 どう 到 いた 同 どう 数 すう 的 てき 一 いち 要 よう 部分 ぶぶん
以斯塔尼 あま 夫 おっと 名 めい 的 てき 一 いち 系列 けいれつ 文章 ぶんしょう 都 と 声 ごえ 称 しょう 的 てき 想 そう 法 ほう 在 ざい 年代 ねんだい 末 まつ 的 てき 波 なみ 流行 りゅうこう 了 りょう 艾 もぐさ 格 かく 是 ぜ 波 は 年代 ねんだい 在 ざい 波 なみ 学 がく 某 ぼう 埃 ほこり 米 まい 将 はた 抽象 ちゅうしょう 形式 けいしき 化 か 的 てき 延 のべ [4] 意 い 理解 りかい 同 どう [來 らい 源 みなもと 請求 せいきゅう 艾 もぐさ 格和 かくわ 麦 むぎ 克 かつ 了 りょう 用 よう 理解 りかい 和 わ 形式 けいしき 化 か 将 はた 代数 だいすう 拓 つぶせ 与 あずか 拓 つぶせ 相 しょう 的 てき 函 はこ 子 こ
范畴论最初 さいしょ 源 げん 自 じ 同 どう 数 すう 的 てき 需要 じゅよう 代数 だいすう 概 がい 形 がた 的 てき 需要 じゅよう 到 いた 被 ひ 泛代数 すう 的 てき 延伸 えんしん 后 きさき 者 しゃ 研究 けんきゅう 代数 だいすう 前者 ぜんしゃ 用 よう 何 なに 数学 すうがく 研究 けんきゅう 不同 ふどう 性 せい 因 いん 用 よう 学 がく 在 ざい 数理 すうり 和 わ 语义 (范畴抽象 ちゅうしょう 机 つくえ )上 じょう 的 てき 来 らい 得 とく
某 ぼう 作 さく 拓 つぶせ 的 てき 可 か 代 だい 公理 こうり 集合 しゅうごう 作 さく 学 がく 的 てき 基 もと 拓 つぶせ 看 み 特定 とくてい 的 てき 有 ゆう 的 てき 拓 つぶせ 公理 こうり 基 もと 用 よう 已 やめ 研究 けんきゅう 得 どく 相当 そうとう 常 つね 是 ぜ 作 さく 数学 すうがく 主 ぬし 的 てき 基 もと 拓 つぶせ 理 り 抽象 ちゅうしょう 层论 的 てき 一 いち 式 しき 源 みなもと 何 なん 学 がく 了 りょう 无点拓 つぶせ 之 これ 法 ほう
范畴逻辑 现在是 ぜ 基 もと 直 ちょく 类型论 ,定 てい 函数 かんすう 式 しき 和 わ 域 いき 理 り 中 ちゅう 得 え 到 いた 一 いち 笛 ふえ 被 ひ λ らむだ 演算 えんざん 的 てき 非 ひ 清 せい 了 りょう 某 ぼう 抽象 ちゅうしょう 意 い 的 てき 共同 きょうどう 点 てん
范畴论还有 ゆう 例 れい 约翰·拜 はい 艾 もぐさ 展示 てんじ 了 りょう 物理 ぶつり 学 がく 中 なか 费曼图 和 かず 之 の [5] 已 やめ 在 ざい 数学 すうがく 音 おん 得 え 到 いた 了 りょう 可 か 参 さん 的 てき 音 おと 拓 つぶせ 概念 がいねん 理 り 表 ひょう 集合 しゅうごう
注 ちゅう [ 编辑 ]
^ 有 ゆう 者 しゃ 會 かい 不同 ふどう 的 てき 次序 じじょ 合 あい 將 はた 寫 うつし 或 ある 研究 けんきゅう 電腦 でんのう 科學 かがく 的 てき 學者 がくしゃ 在 ざい 使用 しよう 範疇 はんちゅう 論 ろん 時 じ 經常 けいじょう 將 しょう
g
∘
f
{\displaystyle g\circ f}
寫 うつし
f
;
g
{\displaystyle f;g}
^ 注意 ちゅうい 双 そう 与 あずか 同 どう 不等 ふとう 一 いち 基本 きほん 的 てき 反例 はんれい 在 ざい 由 よし 物件 ぶっけん
A
,
B
{\displaystyle A,\ B}
与 あずか
f
:
A
→
B
{\displaystyle f:\ A\to B}
的 てき 中 ちゅう
f
{\displaystyle f}
是 ぜ 双 そう 但 ただし 不同 ふどう
參考 さんこう 資料 しりょう [ 编辑 ] 引用 いんよう [ 编辑 ]
^ 1.0 1.1 Eilenberg, Samuel; Mac Lane, Saunders. General theory of natural equivalences (PDF) . Transactions of the American Mathematical Society. 1945, 58 : 247. ISSN 0002-9947 doi:10.1090/S0002-9947-1945-0013131-6 原始 げんし 内容 ないよう 存 そん (PDF) 于2022-10-10). ^ Eilenberg, S.; Mac Lane, S. Group Extensions and Homology 43 (4): 757–831 [2023-05-28 ] . ISSN 0003-486X JSTOR 1968966 doi:10.2307/1968966 原始 げんし 内容 ないよう 存 そん 通 どおり JSTOR . ^ Marquis, Jean-Pierre. Category Theory . Stanford Encyclopedia of Philosophy . Department of Philosophy, Stanford University . 2019 [2022-09-26 ] . (原始 げんし 内容 ないよう 存 そん ^ Reck, Erich. The Prehistory of Mathematical Structuralism 1st. Oxford University Press. 2020: 215–219. ISBN 9780190641221(英 えい . ^ Baez, J.C.; Stay, M. Physics, topology, logic and computation: A Rosetta stone. New Structures for Physics. Lecture Notes in Physics 813 . 2009: 95–172. ISBN 978-3-642-12820-2S2CID 115169297 arXiv:0903.0340 doi:10.1007/978-3-642-12821-9_2
来 らい 源 みなもと [ 编辑 ] Adámek, Jiří; Herrlich, Horst ; Strecker, George E. Abstract and Concrete Categories . Heldermann Verlag Berlin. 2004 [2022-10-09 ] . (原始 げんし 内容 ないよう 存 そん Barr, Michael ; Wells, Charles , Category Theory for Computing Science , Reprints in Theory and Applications of Categories 22 3rd, 2012 [1995] [2022-10-09 ] , (原始 げんし 内容 ないよう 存 そん Barr, Michael ; Wells, Charles , Toposes, Triples and Theories , Reprints in Theory and Applications of Categories 12 , 2005 [2022-10-09 ] , MR 2178101 原始 げんし 内容 ないよう 存 そん Borceux, Francis. Handbook of categorical algebra . Encyclopedia of Mathematics and its Applications. Cambridge University Press. 1994: 50–52. ISBN 9780521441780 Freyd, Peter J. Abelian Categories . Reprints in Theory and Applications of Categories 3 . 2003 [1964] [2022-10-09 ] . (原始 げんし 内容 ないよう 存 そん Freyd, Peter J. ; Scedrov, Andre. Categories, allegories . North Holland Mathematical Library 39 . North Holland. 1990. ISBN 978-0-08-088701-2 Goldblatt, Robert . Topoi: The Categorial Analysis of Logic . Studies in logic and the foundations of mathematics 94 . Dover. 2006 [1979]. ISBN 978-0-486-45026-1 Herrlich, Horst ; Strecker, George E. Category Theory 3rd. Heldermann Verlag Berlin. 2007. ISBN 978-3-88538-001-6 Kashiwara, Masaki ; Schapira, Pierre . Categories and Sheaves . Grundlehren der Mathematischen Wissenschaften 332 . Springer. 2006 [2022-10-09 ] . ISBN 978-3-540-27949-5原始 げんし 内容 ないよう 存 そん Lawvere, F. William ; Rosebrugh, Robert. Sets for Mathematics ISBN 978-0-521-01060-3 Lawvere, F. William; Schanuel, Stephen Hoel . Conceptual Mathematics: A First Introduction to Categories ISBN 978-0-521-89485-2 Leinster, Tom. Higher Operads, Higher Categories . London Math. Society Lecture Note Series 298 . Cambridge University Press. 2004: 448 [2006-04-03 ] . Bibcode:2004hohc.book.....L ISBN 978-0-521-53215-0原始 げんし 内容 ないよう 存 そん Leinster, Tom. Basic Category Theory . Cambridge Studies in Advanced Mathematics 143 . Cambridge University Press. 2014 [2022-10-09 ] . ISBN 9781107044241arXiv:1612.09375 原始 げんし 内容 ないよう 存 そん Lurie, Jacob . Higher Topos Theory. Annals of Mathematics Studies 170 . Princeton University Press. 2009. ISBN 978-0-691-14049-0MR 2522659 arXiv:math.CT/0608040 Mac Lane, Saunders . Categories for the Working Mathematician . Graduate Texts in Mathematics 5 2nd. Springer-Verlag. 1998. ISBN 978-0-387-98403-2MR 1712872 Mac Lane, Saunders ; Birkhoff, Garrett . Algebra 2nd. Chelsea. 1999 [1967]. ISBN 978-0-8218-1646-2 Martini, A.; Ehrig, H.; Nunes, D. Elements of basic category theory . Technical Report. 1996, 96 (5) [2022-10-09 ] . (原始 げんし 内容 ないよう 存 そん May, Peter . A Concise Course in Algebraic Topology. University of Chicago Press. 1999. ISBN 978-0-226-51183-2 Mazzola, Guerino . The Topos of Music, Geometric Logic of Concepts, Theory, and Performance . Birkhäuser. 2002. ISBN 978-3-7643-5731-3 Pedicchio, Maria Cristina; Tholen, Walter (编). Categorical foundations. Special topics in order, topology, algebra, and sheaf theory. Encyclopedia of Mathematics and Its Applications 97 . Cambridge University Press . 2004. ISBN 978-0-521-83414-8Zbl 1034.18001 Pierce, Benjamin C. Basic Category Theory for Computer Scientists . MIT Press. 1991. ISBN 978-0-262-66071-6 Schalk, A.; Simmons, H. An introduction to Category Theory in four easy movements (PDF) . 2005 [2007-12-03 ] . (原始 げんし 内容 ないよう (PDF) 存 そん Mathematical Logic , Manchester University .Simpson, Carlos . Homotopy theory of higher categories . 2010. Bibcode:2010arXiv1001.4071S arXiv:1001.4071 Taylor, Paul. Practical Foundations of Mathematics . Cambridge Studies in Advanced Mathematics 59 . Cambridge University Press. 1999. ISBN 978-0-521-63107-5 Turi, Daniele. Category Theory Lecture Notes (PDF) . 1996–2001 [11 December 2009] . (原始 げんし 内容 ないよう 存 そん (PDF) 于2022-02-21). Mac Lane 1998 .延伸 えんしん [ 编辑 ] 外部 がいぶ [ 编辑 ]

 . Annals of Mathematics. 1942, 43 (4): 757–831 [2023-05-28]. ISSN 0003-486X. JSTOR 1968966. doi:10.2307/1968966. (
. Annals of Mathematics. 1942, 43 (4): 757–831 [2023-05-28]. ISSN 0003-486X. JSTOR 1968966. doi:10.2307/1968966. ( . doi:10.1007/978-3-642-12821-9_2.
. doi:10.1007/978-3-642-12821-9_2.
 . Cambridge University Press. 2003. ISBN 978-0-521-01060-3.
. Cambridge University Press. 2003. ISBN 978-0-521-01060-3. 2nd. Cambridge University Press. 2009 [1997]. ISBN 978-0-521-89485-2.
2nd. Cambridge University Press. 2009 [1997]. ISBN 978-0-521-89485-2. . (
. ( .
. ., draft of a book.
., draft of a book.