正 せい 値 ね 関数 かんすう 積分 せきぶん 曲線 きょくせん 下部 かぶ 軸 じく 囲 かこ 部分 ぶぶん 図 ず 青 あお 塗 ぬ 部分 ぶぶん 面積 めんせき 解釈 かいしゃく 数学 すうがく 一変 いっぺん 数 すう 非負 ひふ 値 ち 関数 かんすう 積分 せきぶん 最 もっと 単純 たんじゅん 場合 ばあい 関数 かんすう x 軸 じく 間 あいだ 面積 めんせき 見 み ルベーグ積分 せきぶん (ルベーグせきぶん、英 えい Lebesgue integral )は、積分 せきぶん 多 おお 関数 かんすう 拡張 かくちょう 積分 せきぶん 被 ひ 積分 せきぶん 関数 かんすう 連続 れんぞく 必要 ひつよう 至 いた 不連続 ふれんぞく 関数 かんすう 値 ち 無限 むげん 大 だい 関数 かんすう 定義 ていぎ 域 いき 拡張 かくちょう 測度 そくど 空間 くうかん 呼 よ 空間 くうかん 定義 ていぎ 関数 かんすう 被 ひ 積分 せきぶん 関数 かんすう
数学 すうがく 者 しゃ 長 なが 間 あいだ 十分 じゅうぶん 滑 なめ 持 も 非負 ひふ 値 ち 関数 かんすう 例 たと 有界 ゆうかい 閉 区間 くかん 上 うえ 連続 れんぞく 関数 かんすう 対 たい 曲線 きょくせん 下部 かぶ 面積 めんせき 積分 せきぶん 定義 ていぎ 理解 りかい 多角 たかく 形 がた 領域 りょういき 近似 きんじ 手法 しゅほう 計算 けいさん 不規則 ふきそく 関数 かんすう 考 かんが 必要 ひつよう 例 たと 解析 かいせき 学 がく 確率 かくりつ 論 ろん 極限 きょくげん 考 かんが 生 しょう 注意深 ちゅういぶか 近似 きんじ 手法 しゅほう 適切 てきせつ 積分 せきぶん 定義 ていぎ 必要 ひつよう 明 あき 局所 きょくしょ 群 ぐん 実数 じっすう 直線 ちょくせん 一般 いっぱん 空間 くうかん 上 じょう 積分 せきぶん 積分 せきぶん 重要 じゅうよう 仕事 しごと 必要 ひつよう 正 ただ 抽象 ちゅうしょう 化 か 与 あた 例 たと フーリエ級数 きゅうすう などの関数 かんすう 列 れつ 極限 きょくげん 表 あらわ 関数 かんすう 対 たい 積分 せきぶん 極限 きょくげん 操作 そうさ 可 か 換 かわ リーマン積分 せきぶん で考 かんが 非常 ひじょう 繊細 せんさい 議論 ぎろん 必要 ひつよう 積分 せきぶん 積分 せきぶん 極限 きょくげん 操作 そうさ 交換 こうかん 可能 かのう 簡単 かんたん 十 じゅう 分 ふん 条件 じょうけん 分 わ
ルベーグ積分 せきぶん 実 じつ 解析 かいせき 呼 よ 数学 すうがく 分野 ぶんや 属 ぞく 確率 かくりつ 論 ろん 他 た 多 おお 数理 すうり 科学 かがく 分野 ぶんや 重要 じゅうよう 役割 やくわり 果 は 積分 せきぶん 名前 なまえ 積分 せきぶん 導入 どうにゅう 数学 すうがく 者 しゃ アンリ・ルベーグ [ 2] 由来 ゆらい 公理 こうり 的 てき 確率 かくりつ 論 ろん (英語 えいご 版 ばん 中枢 ちゅうすう 部 ぶ
「ルベーグ積分 せきぶん 用語 ようご カラテオドリ に始 はじ 一般 いっぱん 測度 そくど 関 かん 関数 かんすう 積分 せきぶん 一般 いっぱん 論 ろん 意味 いみ ルベーグ測度 そくど に関 かん 実数 じっすう 直線 ちょくせん n -次元 じげん ユークリッド空間 くうかん )の特定 とくてい 部分 ぶぶん 集合 しゅうごう 特 とく ルベーグ可 か 測 はか 集合 しゅうごう )上 じょう 定義 ていぎ ルベーグ可 か 測 はか 関数 かんすう を積分 せきぶん 特定 とくてい 場合 ばあい 意味 いみ
積分 せきぶん 厳密 げんみつ 動 うご 19世紀 せいき からである。ベルンハルト・リーマン が提案 ていあん 積分 せきぶん 目的 もくてき 向 む 大 おお 前進 ぜんしん 関数 かんすう 積分 せきぶん 簡単 かんたん 計算 けいさん 積分 せきぶん 近似 きんじ 定義 ていぎ 定義 ていぎ 積分 せきぶん 解答 かいとう 知 し 問題 もんだい 対 たい 結果 けっか 他 た 問題 もんだい 対 たい 新 あたら 結果 けっか 与 あた 積分 せきぶん 関数 かんすう 列 れつ 極限 きょくげん 相性 あいしょう 悪 わる 積分 せきぶん 極限 きょくげん 同時 どうじ 現 あらわ 場面 ばめん 解析 かいせき 困難 こんなん 場合 ばあい 対 たい 積分 せきぶん 積分 せきぶん 記号 きごう 下 した 極限 きょくげん 扱 あつか 積分 せきぶん 積分 せきぶん 異 こと 形 かたち 簡単 かんたん 計算 けいさん 積分 せきぶん 考 かんが 積分 せきぶん 積分 せきぶん 振舞 ふるま 理由 りゆう 積分 せきぶん 積分 せきぶん 広 ひろ 種類 しゅるい 関数 かんすう 対 たい 積分 せきぶん 定義 ていぎ 可能 かのう 例 たと 無理 むり 数 すう 有理数 ゆうりすう 関数 かんすう ディリクレの関数 かんすう )を閉区間 あいだ [0, 1] 上 じょう 考 かんが 積分 せきぶん 積分 せきぶん 定義 ていぎ 積分 せきぶん 積分 せきぶん
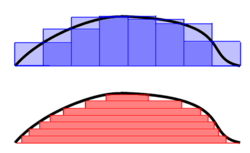
リーマン積分 せきぶん 青 あお 積分 せきぶん 赤 あか 積分 せきぶん 定義 ていぎ 方法 ほうほう 違 ちが 直感 ちょっかん 的 てき 理解 りかい 山 やま 海抜 かいばつ 上 うえ 部分 ぶぶん 体積 たいせき 計算 けいさん 例 れい 考 かんが 山 やま 境界 きょうかい 定 さだ 積分 せきぶん 範囲 はんい
リーマン積分 せきぶん 方法 ほうほう
ケーキを切 き 山 やま 縦 たて 方向 ほうこう 切 き 分 わ 細分 さいぶん 各 かく 底面 ていめん 長方形 ちょうほうけい 次 つぎ 各 かく 最 もっと 標高 ひょうこう 高 たか 調 しら 底面 ていめん 面積 めんせき 標高 ひょうこう 掛 か 合 あ 各 かく 計算 けいさん 値 ね 足 た 上 うえ 和 わ 呼 よ 同様 どうよう 最 もっと 標高 ひょうこう 低 ひく 対 たい 行 おこな 下 しも 和 わ 呼 よ 分割 ぶんかつ 細 こま 上 うえ 下 した 和 わ 同 おな 値 ち 収束 しゅうそく 積分 せきぶん 可能 かのう 極限 きょくげん 値 ち 山 やま 体積 たいせき
ルベーグ積分 せきぶん 方法 ほうほう
山 やま 等高線 とうこうせん 地図 ちず 等高線 とうこうせん 地図 ちず 裁断 さいだん 地図 ちず 分解 ぶんかい 各 かく 面積 めんせき 計算 けいさん 平面 へいめん 図形 ずけい 測度 そくど 分 わ 面積 めんせき 最 もっと 低 ひく 点 てん 標高 ひょうこう 掛 か 合 あ 各 かく 値 ね 足 た 和 わ 呼 よ 和 わ 積分 せきぶん 構成 こうせい 単 たん 関数 かんすう 積分 せきぶん 相当 そうとう 等高線 とうこうせん 間隔 かんかく 半分 はんぶん 和 わ 極限 きょくげん 値 ち 山 やま 体積 たいせき 有理数 ゆうりすう 体 たい
Q
{\displaystyle \mathbb {Q} }
定義 ていぎ 関数 かんすう
1
Q
{\displaystyle 1_{\mathbf {Q} }}
ディリクレの関数 かんすう )を考 かんが 関数 かんすう 至 いた 不連続 ふれんぞく
1
Q
{\displaystyle 1_{\mathbf {Q} }}
は [0, 1] 上 うえ 可 か 積分 せきぶん 区間 くかん 分割 ぶんかつ 各 かく 区間 くかん 有理数 ゆうりすう 無理 むり 数 すう 両方 りょうほう 少 すく 入 はい 上積 うわづみ 分 ぶん 常 つね 下 しも 積分 せきぶん 常 つね 可 か 積分 せきぶん
1
Q
{\displaystyle 1_{\mathbf {Q} }}
は [0, 1] 上 うえ 可 か 積分 せきぶん 集合 しゅうごう 定義 ていぎ 関数 かんすう 積分 せきぶん 定義 ていぎ
∫
[
0
,
1
]
1
Q
d
μ みゅー =
μ みゅー (
Q
∩
[
0
,
1
]
)
=
0
{\displaystyle \int _{[0,1]}1_{\mathbf {Q} }\,d\mu =\mu (\mathbf {Q} \cap [0,1])=0}
ルベーグ積分 せきぶん 定義 ていぎ 測度 そくど 概念 がいねん 必要 ひつよう 言 い 実数 じっすう 集合 しゅうごう A に対 たい 集合 しゅうごう A の「大 おお 非負 ひふ 実数 じっすう μ みゅー A )割 わ 当 あ 大 おお 区間 くかん 区間 くかん 非 ひ 対 たい 通常 つうじょう 意味 いみ 長 なが 一致 いっち 函数 かんすう
f
:
R
→
R
+
{\displaystyle f:{\mathbb {R} }\rightarrow {\mathbb {R} }^{+}}
非負 ひふ 実 じつ 数値 すうち 函数 かんすう f の値域 ちいき 分割 ぶんかつ 考 かんが f の積分 せきぶん y = t y = t + dt 間 あいだ 水平 すいへい 細 ほそ 帯状 おびじょう 領域 りょういき 占 し 基本 きほん 面積 めんせき t に関 かん 加 くわ 総和 そうわ 基本 きほん 面積 めんせき
μ みゅー (
{
x
∣
f
(
x
)
>
t
}
)
d
t
{\displaystyle \mu (\{x\mid f(x)>t\})\mathrm {d} t}
等 ひと
f
∗
(
t
)
:=
μ みゅー (
{
x
∣
f
(
x
)
>
t
}
)
{\displaystyle f^{*}(t):=\mu (\{x\mid f(x)>t\})}
置 お f のルベーグ積分 せきぶん
∫
f
d
μ みゅー =
∫
Ω おめが
f
(
t
)
μ みゅー (
d
t
)
:=
∫
0
∞
f
∗
(
t
)
d
t
{\displaystyle \int f\,\mathrm {d} \mu =\int _{\Omega }f(t)\,\mu (\mathrm {d} t):=\int _{0}^{\infty }f^{*}(t)\,\mathrm {d} t}
定義 ていぎ 右辺 うへん 積分 せきぶん 広義 こうぎ 積分 せきぶん 意味 いみ f* が非負 ひふ 単調 たんちょう 増大 ぞうだい 函数 かんすう 区間 くかん [
0
,
∞
{\displaystyle 0,\infty }
に値 ね 広義 こうぎ 積分 せきぶん 定 さだ 注意 ちゅうい 可 か 測 はか 函数 かんすう 属 ぞく 函数 かんすう 対 たい 積分 せきぶん 定義 ていぎ
一般 いっぱん 非負 ひふ 限 かぎ 可 か 測 はか 函数 かんすう f がルベーグ可 か 積分 せきぶん f のグラフと x -軸 じく 囲 かこ 領域 りょういき 面積 めんせき 有限 ゆうげん
∫
|
f
|
d
μ みゅー <
+
∞
{\displaystyle \int |f|\,\mathrm {d} \mu <+\infty }
場合 ばあい 積分 せきぶん 値 ね 積分 せきぶん 同様 どうよう x -軸 じく 上 うえ 面積 めんせき x -軸 じく 下 した 面積 めんせき 引 ひ
∫
f
d
μ みゅー =
∫
f
+
d
μ みゅー −
∫
f
−
d
μ みゅー
{\displaystyle \int f\,\mathrm {d} \mu =\int f^{+}\,\mathrm {d} \mu -\int f^{-}\,\mathrm {d} \mu }
与 あた
f
=
f
+
−
f
−
{\textstyle f=f^{+}-f^{-}}
f の二 ふた 非負 ひふ 値 ち 函数 かんすう 分解 ぶんかい 各々 おのおの
f
+
(
x
)
=
max
{
f
(
x
)
,
0
}
=
{
f
(
x
)
,
if
f
(
x
)
>
0
,
0
,
otherwise
f
−
(
x
)
=
max
{
−
f
(
x
)
,
0
}
=
{
−
f
(
x
)
,
if
f
(
x
)
<
0
,
0
,
otherwise.
{\displaystyle {\begin{aligned}f^{+}(x)&=\max\{f(x),0\}&&{}={\begin{cases}f(x),&{\text{if }}f(x)>0,\\0,&{\text{otherwise}}\end{cases}}\\f^{-}(x)&=\max\{-f(x),0\}&&{}={\begin{cases}-f(x),&{\text{if }}f(x)<0,\\0,&{\text{otherwise.}}\end{cases}}\end{aligned}}}
与 あた
ルベーグ積分 せきぶん 論 ろん 可 か 測 はか 集合 しゅうごう 上 うえ 測度 そくど 関 かん 理論 りろん 測度 そくど 論 ろん 可 か 測 はか 函数 かんすう 積分 せきぶん 関 かん 理論 りろん 積分 せきぶん 論 ろん 二 に 段 だん 構 かま
当初 とうしょ 測度 そくど 論 ろん 線分 せんぶん 平面 へいめん 図形 ずけい 立体 りったい 長 なが 面積 めんせき 体積 たいせき 精密 せいみつ 解析 かいせき 考 かんが 出 だ Lebesgue 1902 )。特 とく 実数 じっすう 全体 ぜんたい 集合 しゅうごう
R
{\displaystyle \mathbb {R} }
部分 ぶぶん 集合 しゅうごう 部分 ぶぶん 集合 しゅうごう 長 なが 何 なに 問 と 対 たい 整然 せいぜん 解答 かいとう 与 あた
集合 しゅうごう 論 ろん 発展 はってん 自然 しぜん 加法 かほう 性 せい 持 も 平行 へいこう 移動 いどう 不変 ふへん 実数 じっすう 体 たい
R
{\displaystyle \mathbb {R} }
部分 ぶぶん 集合 しゅうごう 長 なが 定義 ていぎ 不可能 ふかのう 可 か 測 はか 集合 しゅうごう 呼 よ 種類 しゅるい 部分 ぶぶん 集合 しゅうごう 長 なが 定義 ていぎ 必要 ひつよう 生 う 測度 そくど 満 み 適当 てきとう 条件 じょうけん 測度 そくど 論 ろん 参照 さんしょう
現代 げんだい 測度 そくど 積分 せきぶん 公理 こうり 的 てき 定義 ていぎ 測度 そくど 集合 しゅうごう X の適当 てきとう 条件 じょうけん 満 み 部分 ぶぶん 集合 しゅうごう 族 ぞく Σ しぐま 上 うえ 定義 ていぎ 適当 てきとう 条件 じょうけん 満 み 関数 かんすう μ みゅー 何 なん X がユークリッド空間 くうかん であったり、Σ しぐま 元 もと 面積 めんせき 計算 けいさん 図形 ずけい 必要 ひつよう μ みゅー 値 ね 面積 めんせき 離 はな 空間 くうかん 図形 ずけい 面積 めんせき 与 あた 測度 そくど 特別 とくべつ ルベーグ測度 そくど という名前 なまえ
リーマン積分 せきぶん 長方形 ちょうほうけい a , b ] × [c , d ] の面積 めんせき b − a )(d − c ) で計算 けいさん 基礎 きそ 積分 せきぶん 積分 せきぶん 近似 きんじ 簡単 かんたん 計算 けいさん 積分 せきぶん 長方形 ちょうほうけい 並 なら 使 つか 測度 そくど 関 かん 深 ふか 議論 ぎろん 必要 ひつよう
測度 そくど 空間 くうかん X , M , μ みゅー 与 あた 例 たと X としてユークリッド空間 くうかん 、M をルベーグ可 か 測 はか 集合 しゅうごう 全体 ぜんたい μ みゅー 測度 そくど 考 かんが 確率 かくりつ 論 ろん 測度 そくど 空間 くうかん μ みゅー X ) = 1 であるような測度 そくど 空間 くうかん 確 かく 率 りつ 空間 くうかん 使 つか
ルベーグ積分 せきぶん 被 ひ 積分 せきぶん 関数 かんすう 関数 かんすう 可 か 測 はか 関数 かんすう 呼 よ 関数 かんすう X 上 うえ 定義 ていぎ 実数 じっすう
±
∞
{\displaystyle \pm \infty }
値 ね 関数 かんすう f が可 か 測 はか 関数 かんすう M -可 か 測 はか 関数 かんすう 任意 にんい 実数 じっすう
a
{\displaystyle a}
(
a
,
+
∞
]
=
(
a
,
+
∞
)
∪
{
+
∞
}
{\displaystyle (a,+\infty ]=(a,+\infty )\cup \{+\infty \}}
f による逆 ぎゃく 像 ぞう M に属 ぞく
f
−
1
(
(
a
,
∞
]
)
∈
M
{\displaystyle f^{-1}((a,\infty ])\in M}
が成 な 立 た 複素数 ふくそすう 値 ね 関数 かんすう 実 み 部 ぶ 虚 きょ 部 ぶ 共 とも 可 か 測 はか 関数 かんすう 可 か 測 はか 関数 かんすう M -可 か 測 はか 関数 かんすう 関数 かんすう 可 か 測 はか 性 せい 定 さだ 可 か 測 はか 関数 かんすう 全体 ぜんたい 集合 しゅうごう 代数 だいすう 的 てき 操作 そうさ 和 わ 差 さ 積 せき 商 しょう 実 じつ 数 すう 倍 ばい 複素 ふくそ 数 すう 倍 ばい 関 かん 閉 と 分 わ 可 か 測 はか 関数 かんすう 全体 ぜんたい 集合 しゅうごう 実数 じっすう 体 からだ 複素数 ふくそすう 体 たい 上 うえ 線型 せんけい 空間 くうかん 成 な 分 わ 完全 かんぜん 加法 かほう 族 ぞく M の性質 せいしつ
R
∪
{
+
∞
,
−
∞
}
{\displaystyle \mathbb {R} \cup \{+\infty ,-\infty \}}
任意 にんい 部分 ぶぶん 集合 しゅうごう I の可 か 測 はか 関数 かんすう f による逆 ぎゃく 像 ぞう f −1 (I ) も M に属 ぞく 分 わ 重要 じゅうよう 多 おお 関数 かんすう 列 れつ 極限 きょくげん 関 かん 閉 と 例 たと 可 か 測 はか 関数 かんすう 列 れつ f k 対 たい
lim
_
k
∈
N
f
k
,
lim
¯
k
∈
N
f
k
{\displaystyle \varliminf _{k\in \mathbb {N} }f_{k},\quad \varlimsup _{k\in \mathbb {N} }f_{k}}
で与 あた 関数 かんすう 可 か 測 はか 関数 かんすう 従 したが 可 か 測 はか 関数 かんすう 列 れつ 各 かく 点 てん 収束 しゅうそく 極限 きょくげん 関数 かんすう 可 か 測 はか 関数 かんすう
X の部分 ぶぶん 集合 しゅうごう E 上 うえ 定義 ていぎ 実 じつ 数値 すうち 可 か 測 はか 函数 かんすう f に対 たい 積分 せきぶん
∫
E
f
d
μ みゅー =
∫
E
f
(
x
)
d
μ みゅー (
x
)
{\displaystyle \int _{E}f\,d\mu =\int _{E}f(x)d\mu (x)}
定義 ていぎ 方法 ほうほう
単 たん 函数 かんすう 近似 きんじ ルベーグ積分 せきぶん 定式 ていしき 化 か 一 ひと 方法 ほうほう 単 たん 函数 かんすう 有限 ゆうげん 個 こ 指示 しじ 函数 かんすう 実 じつ 係数 けいすう 線型 せんけい 結合 けつごう 用 もち 単 たん 函数 かんすう 可 か 測 はか 函数 かんすう 値域 ちいき 帯状 おびじょう 分割 ぶんかつ 可 か 測 はか 函数 かんすう 近似 きんじ 単 たん 函数 かんすう 積分 せきぶん 各 かく 帯状 おびじょう 領域 りょういき 測度 そくど 高 たか 掛 か 等 ひと 非負 ひふ 値 ち 一般 いっぱん 可 か 測 はか 函数 かんすう 積分 せきぶん 函数 かんすう 単 たん 函数 かんすう 近似 きんじ 上限 じょうげん 定義 ていぎ 非負 ひふ 限 かぎ 場合 ばあい 函数 かんすう 正 せい 成分 せいぶん 負 ふ 成分 せいぶん 二 ふた 非負 ひふ 値 ち 函数 かんすう 差 さ 分解 ぶんかい 積分 せきぶん 差 さ 可 か 測 はか 函数 かんすう 積分 せきぶん 定義 ていぎ
与 あた 測度 そくど μ みゅー 関 かん 可 か 測 はか 集合 しゅうごう S に対 たい S の定義 ていぎ 関数 かんすう
1
S
{\displaystyle 1_{S}}
積分 せきぶん
∫
X
1
S
d
μ みゅー :=
μ みゅー (
S
)
{\displaystyle \int _{X}1_{S}\,d\mu :=\mu (S)}
測度 そくど μ みゅー 有限 ゆうげん 測度 そくど 限 かぎ 積分 せきぶん 値 ち
+
∞
{\displaystyle +\infty }
場合 ばあい 注意 ちゅうい 以下 いか 積分 せきぶん
+
∞
{\displaystyle +\infty }
場合 ばあい 許 ゆる 積分 せきぶん 存在 そんざい 言 い
実数 じっすう 定数 ていすう 列 れつ ak と μ みゅー 可 か 測 はか 集合 しゅうごう 列 れつ Sk から作 つく 有限 ゆうげん 線型 せんけい 結合 けつごう
∑
k
a
k
1
S
k
{\displaystyle \sum _{k}a_{k}1_{S_{k}}}
可 か 測 はか 単 たん 函数 かんすう 呼 よ 可 か 測 はか 単 たん 函数 かんすう 積分 せきぶん 指示 しじ 函数 かんすう 積分 せきぶん 線型 せんけい 拡張 かくちょう 与 あた 詳 くわ 書 か 非負 ひふ 値 ち 可 か 測 はか 単 たん 函数 かんすう ak > 0 (∀k )場合 ばあい 対 たい 積分 せきぶん
∫
X
(
∑
k
a
k
1
S
k
)
d
μ みゅー :=
∑
k
a
k
∫
X
1
S
k
d
μ みゅー =
∑
k
a
k
μ みゅー (
S
k
)
{\displaystyle \int _{X}{\Bigl (}\sum _{k}a_{k}1_{S_{k}}{\Bigr )}\,d\mu :=\sum _{k}a_{k}\int _{X}1_{S_{k}}\,d\mu =\sum _{k}a_{k}\mu (S_{k})}
定 さだ
0
×
∞
{\displaystyle 0\times \infty }
不 ふ 定形 ていけい 生 しょう 場合 ばあい 想定 そうてい 規約 きやく
0
×
∞
=
0
{\displaystyle 0\times \infty =0}
用 もち 前 ぜん 目 め 同 おな 積分 せきぶん
∞
{\displaystyle \infty }
得 え
与 あた 単 たん 函数 かんすう 指示 しじ 函数 かんすう 線型 せんけい 結合 けつごう 表 あらわ 方法 ほうほう 複数 ふくすう 上記 じょうき 定義 ていぎ 積分 せきぶん 常 つね 同 おな 値 ち 留意 りゅうい 測度 そくど 加法 かほう 性 せい
非負 ひふ 限 かぎ 一般 いっぱん 実 じつ 数値 すうち 単 たん 函数 かんすう 場合 ばあい 同様 どうよう 不 ふ 定形 ていけい
∞
−
∞
{\displaystyle \infty -\infty }
値 ね 定義 ていぎ 無意味 むいみ 扱 あつか 現 あらわ 避 さ 非負 ひふ 限 かぎ f であってもそれを
f
=
∑
k
a
k
1
S
k
{\displaystyle f=\sum _{k}a_{k}1_{S_{k}}}
表 あらわ ak ≠ 0場合 ばあい 必 かなら
μ みゅー (
S
k
)
≤
∞
{\displaystyle \mu (S_{k})\leq \infty }
仮定 かてい 満 み 上 うえ 述 の 積分 せきぶん 定義 ていぎ 式 しき 意味 いみ 為 な 非負 ひふ 値 ち 場合 ばあい 同様 どうよう 表 あらわ 方 かた 依 よ 定 さだ
X の可 か 測 はか 部分 ぶぶん 集合 しゅうごう B と可 か 測 はか 単 たん 函数 かんすう s に対 たい 積分 せきぶん 領域 りょういき B 上 うえ s の積分 せきぶん
∫
B
s
d
μ みゅー =
∫
1
B
s
d
μ みゅー =
∑
k
a
k
μ みゅー (
S
k
∩
B
)
{\displaystyle \int _{B}s\,d\mu =\int 1_{B}\,s\,d\mu =\sum _{k}a_{k}\,\mu (S_{k}\cap B)}
与 あた
非負 ひふ 値 ち 可 か 測 はか 関数 かんすう
∞
{\displaystyle \infty }
値 ね 許 ゆる f の積分 せきぶん
∫
X
f
d
μ みゅー =
sup
s
↑
f
{
∫
X
s
d
μ みゅー ∣
s
:
simple, non-negative
}
{\displaystyle \int _{X}f\,d\mu =\sup _{s\uparrow f}\{\int _{X}s\,d\mu \mid s\colon {\text{ simple, non-negative}}\}}
で定 さだ 拡張 かくちょう 実数 じっすう 値 ち 実数 じっすう 以外 いがい
±
∞
{\displaystyle \pm \infty }
値 ね 許 ゆる 可 か 測 はか 函数 かんすう f の積分 せきぶん f を正 せい 成分 せいぶん f+ と負 ふ 成分 せいぶん f− の差 さ
f
=
f
+
−
f
−
{\displaystyle f=f^{+}-f^{-}}
分解 ぶんかい f + (x ) = max{f (x ), 0}, f − (x ) = −min{0, f (x )}
|
f
|
=
f
+
+
f
−
{\textstyle |f|=f^{+}+f^{-}}
非負 ひふ 可 か 測 はか 函数 かんすう 注意 ちゅうい
∫
X
f
d
μ みゅー :=
∫
X
f
+
d
μ みゅー −
∫
X
f
−
d
μ みゅー
{\displaystyle \int _{X}f\,d\mu :=\int _{X}f^{+}d\mu -\int _{X}f^{-}d\mu }
定義 ていぎ 左辺 さへん 積分 せきぶん ±∞ の場合 ばあい 許 ゆる 存在 そんざい 右辺 うへん 二 ふた 積分 せきぶん 一 ひと 有限 ゆうげん 値 ち 留意 りゅうい f が可 か 積分 せきぶん 左辺 さへん 存在 そんざい 有限 ゆうげん 確定 かくてい 値 ち 要求 ようきゅう 非負 ひふ 限 かぎ 拡張 かくちょう 実 じつ 数値 すうち 可 か 測 はか 函数 かんすう f がルベーグ可 か 積分 せきぶん 必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん
∫
X
f
+
d
μ みゅー <
∞
∧
∫
X
f
−
d
μ みゅー <
∞
(
⟺
∫
X
|
f
|
d
μ みゅー <
∞
)
{\displaystyle \int _{X}f^{+}\,d\mu <\infty \land \int _{X}f^{-}\,d\mu <\infty \qquad (\iff \int _{X}{\mathopen {|}}f{\mathclose {|}}d\mu <\infty )}
絶対 ぜったい 値 ち 積分 せきぶん 有限 ゆうげん 確定 かくてい 意味 いみ 絶対 ぜったい 可 か 積分 せきぶん
複素 ふくそ 数値 すうち 可 か 測 はか 函数 かんすう 場合 ばあい 同様 どうよう 積分 せきぶん 函数 かんすう 実 み 部 ぶ 虚 きょ 部 ぶ 和 わ 分解 ぶんかい 定義 ていぎ 複素 ふくそ 数値 すうち 可 か 測 はか 函数 かんすう h が実 じつ 数値 すうち 可 か 積分 せきぶん 函数 かんすう f, g を用 もち h = f + ig 書 か h の積分 せきぶん
∫
X
h
d
μ みゅー =
∫
f
d
μ みゅー +
i
∫
g
d
μ みゅー
{\displaystyle \int _{X}h\,d\mu =\int f\,d\mu +i\int g\,d\mu }
定義 ていぎ
複素 ふくそ 数値 すうち 可 か 測 はか 函数 かんすう 可 か 積分 せきぶん 必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん 絶対 ぜったい 値 ち 可 か 積分 せきぶん
ルベーグ積分 せきぶん 技術 ぎじゅつ 的 てき 目的 もくてき 積分 せきぶん 領域 りょういき 可 か 測 はか 空間 くうかん 適当 てきとう 部分 ぶぶん 集合 しゅうごう 集合 しゅうごう 積分 せきぶん 領域 りょういき 向 む 持 も 留意 りゅうい 初等 しょとう 的 てき 微分 びぶん 積分 せきぶん 学 がく 積分 せきぶん 向 む 反映 はんえい
∫
b
a
f
:=
−
∫
a
b
f
{\displaystyle \int _{b}^{a}f:=-\int _{a}^{b}f}
定義 ていぎ 高階 たかしな 微分 びぶん 形式 けいしき 積分 せきぶん 場合 ばあい 一般 いっぱん 化 か 対照 たいしょう 積分 せきぶん 部分 ぶぶん 集合 しゅうごう 測度 そくど 関 かん 積分 せきぶん 別 べつ 方向 ほうこう 一般 いっぱん 化 か 与 あた 一次元 いちじげん 積分 せきぶん 区間 くかん A = [a , b ]
∫
A
f
d
μ みゅー =
∫
[
a
,
b
]
f
d
μ みゅー
{\displaystyle \int _{A}f\,d\mu =\int _{[a,b]}f\,d\mu }
書 か 部分 ぶぶん 集合 しゅうごう [a , b ] での積分 せきぶん 示唆 しさ 可能 かのう a > b 間 あいだ A は空 そら 集合 しゅうごう 場合 ばあい 積分 せきぶん 値 ち 0 である。
ルベーグ積分 せきぶん 零 れい 集合 しゅうごう 上 うえ 異 こと 値 ね 関数 かんすう 区別 くべつ 正確 せいかく 言 い 関数 かんすう f と g がほとんど至 いた 等 ひと
μ みゅー (
{
x
:
f
(
x
)
≠
g
(
x
)
}
)
=
0
{\displaystyle \mu (\{x:f(x)\neq g(x)\})=0}
をみたすことであり、
f
=
g
a.e.
{\displaystyle f=g\quad {\text{a.e.}}}
と書 か
非負 ひふ 値 ち 可 か 測 はか 関数 かんすう
∞
{\displaystyle \infty }
関数 かんすう 値 ち 許 ゆる f と g がほとんど至 いた 等 ひと
∫
E
f
d
μ みゅー =
∫
E
g
d
μ みゅー .
{\displaystyle \int _{E}f\,d\mu =\int _{E}g\,d\mu .}
可 か 測 はか 関数 かんすう
±
∞
{\displaystyle \pm \infty }
関数 かんすう 値 ち 許 ゆる f と g がほとんど至 いた 等 ひと f が可 か 積分 せきぶん g が可 か 積分 せきぶん 同値 どうち 積分 せきぶん 値 ね 等 ひと ルベーグ積分 せきぶん 以下 いか 性質 せいしつ 持 も
線型 せんけい 性 せい 可 か 積分 せきぶん 関数 かんすう f , g と実数 じっすう a , b に対 たい af + bg も可 か 積分 せきぶん
∫
E
(
a
f
+
b
g
)
d
μ みゅー =
a
∫
E
f
d
μ みゅー +
b
∫
E
g
d
μ みゅー
{\displaystyle \int _{E}(af+bg)\,d\mu =a\int _{E}f\,d\mu +b\int _{E}g\,d\mu \,}
単調 たんちょう 性 せい f ≤ g ならば
∫
E
f
d
μ みゅー ≤
∫
E
g
d
μ みゅー
{\displaystyle \int _{E}f\,d\mu \leq \int _{E}g\,d\mu }
単調 たんちょう 収束 しゅうそく 定理 ていり f k k ∈N 非負 ひふ 値 ち 可 か 測 はか 関数 かんすう 増大 ぞうだい 列 れつ
0
≤
f
k
(
x
)
≤
f
k
+
1
(
x
)
∀
k
∈
N
,
a.e.
x
∈
E
.
{\displaystyle 0\leq f_{k}(x)\leq f_{k+1}(x)\quad \forall k\in \mathbb {N} ,{\text{ a.e. }}\ x\in E.}
このとき
lim
k
∫
f
k
d
μ みゅー =
∫
lim
k
f
k
d
μ みゅー .
{\displaystyle \lim _{k}\int f_{k}\,d\mu =\int \lim _{k}f_{k}\,d\mu .}
が成立 せいりつ
注意 ちゅうい 左辺 さへん 右辺 うへん 一方 いっぽう 正 せい 無限 むげん 大 だい 発散 はっさん 一方 いっぽう 辺 あたり 同様 どうよう
ファトゥーの補題 ほだい : {f k k ∈N 非負 ひふ 値 ち 可 か 測 はか 関数 かんすう 列 れつ
∫
lim
_
k
f
k
d
μ みゅー ≤
lim
_
k
∫
f
k
d
μ みゅー
{\displaystyle \int \varliminf _{k}f_{k}\,d\mu \leq \varliminf _{k}\int f_{k}\,d\mu }
が成立 せいりつ
この定理 ていり 左辺 さへん 正 せい 無限 むげん 大 だい 発散 はっさん 右辺 うへん 正 せい 無限 むげん 大 だい 発散 はっさん
ルベーグの収束 しゅうそく 定理 ていり : {f k k ∈N 可 か 測 はか 関数 かんすう 列 れつ f に概 がい 収束 しゅうそく 可 か 積分 せきぶん 関数 かんすう g によって、 E のほとんど至 いた 任意 にんい k に対 たい f k g と上下 じょうげ 押 お 極限 きょくげん 関数 かんすう f も可 か 積分 せきぶん
lim
k
∫
f
k
d
μ みゅー =
∫
f
d
μ みゅー
{\displaystyle \lim _{k}\int f_{k}\,d\mu =\int f\,d\mu }
が成立 せいりつ
測度 そくど 論 ろん 全 まった 使 つか 方法 ほうほう 積分 せきぶん コンパクト 台 だい 持 も 任意 にんい 連続 れんぞく 関数 かんすう 対 たい 定 さだ 関数 かんすう 解析 かいせき 手法 しゅほう 用 もち 一般 いっぱん 関数 かんすう 積分 せきぶん 拡張 かくちょう 方法 ほうほう Cc を R 上 うえ 定義 ていぎ 実 じつ 数値 すうち 関数 かんすう 台 だい 持 も 全体 ぜんたい 積分 せきぶん 用 もち
‖
f
‖
=
∫
|
f
(
x
)
|
d
x
{\displaystyle \|f\|=\int |f(x)|\,dx}
により定 さだ
これにより Cc は線形 せんけい 空間 くうかん 距離 きょり 空間 くうかん 完備 かんび 化 か 完備 かんび 空間 くうかん 拡張 かくちょう L 1 とする。この空間 くうかん 可 か 積分 せきぶん 関数 かんすう 空間 くうかん 至 いた 等 ひと 関数 かんすう 同一 どういつ 視 し 同型 どうけい 積分 せきぶん Cc 上 うえ 連続 れんぞく 線形 せんけい 汎 ひろし 関数 かんすう Cc は L 1 の稠密 ちゅうみつ 部分 ぶぶん 空間 くうかん L 1 上 うえ 線形 せんけい 汎 ひろし 関数 かんすう 一 いち 通 とお 拡張 かくちょう 拡張 かくちょう 積分 せきぶん 一致 いっち
この方法 ほうほう 問題 もんだい 点 てん 関数 かんすう 空間 くうかん 点 てん 定 さだ 抽象 ちゅうしょう 的 てき 点 てん 関数 かんすう 表現 ひょうげん 方法 ほうほう 自明 じめい 関数 かんすう 列 れつ 各 かく 点 てん 収束 しゅうそく 積分 せきぶん 関係 かんけい 示 しめ 非常 ひじょう 難 むずか 一般 いっぱん 化 か 局所 きょくしょ 空間 くうかん 上 うえ ラドン測度 そくど に関 かん 積分 せきぶん 理論 りろん 構築 こうちく Bourbaki (2004) によって採用 さいよう 詳細 しょうさい 局所 きょくしょ 空間 くうかん 上 じょう 測度 そくど 参照 さんしょう
高木 たかぎ 貞治 さだはる 定本 ていほん 解析 かいせき 概論 がいろん 岩波書店 いわなみしょてん 寺澤 てらさわ 順 じゅん 積分 せきぶん 日本 にっぽん 評論 ひょうろん 社 しゃ 猪狩 いかり 実 じつ 解析 かいせき 入門 にゅうもん 岩波書店 いわなみしょてん 「数学 すうがく 年 ねん 月 がつ 号 ごう 日本 にっぽん 評論 ひょうろん 社 しゃ 実 じつ 解析 かいせき 何 なに
新井 あらい 仁之 ひとし 積分 せきぶん 講義 こうぎ 日本 にっぽん 評論 ひょうろん 社 しゃ 森 もり 真 しん 積分 せきぶん 超 ちょう 入門 にゅうもん 共立 きょうりつ 出版 しゅっぱん 松浦 まつうら 武信 たけのぶ 高橋 たかはし 宣明 のぶあき 吉田 よしだ 正廣 まさひろ 物理 ぶつり 工学 こうがく 積分 せきぶん 入門 にゅうもん 東海大学 とうかいだいがく 出版 しゅっぱん 会 かい 谷島 やじま 賢二 けんじ 積分 せきぶん 関数 かんすう 解析 かいせき 朝倉書店 あさくらしょてん 谷島 やじま 賢二 けんじ 新版 しんぱん 積分 せきぶん 関数 かんすう 解析 かいせき 朝倉書店 あさくらしょてん 黒田 くろだ 成俊 なりとし 関数 かんすう 解析 かいせき 共立 きょうりつ 出版 しゅっぱん 伊藤 いとう 清三 せいぞう 積分 せきぶん 入門 にゅうもん 裳 も 華 はな 房 ぼう 竹之内 たけのうち 脩 おさむ 積分 せきぶん 培風館 ばいふうかん R. M. Dudley, Real Analysis and Probability , Wadsworth & Brookes/Cole, 1989. [ * 1]
P. R. Halmos, Measure Theory , D. van Nostrand Company, Inc. 1950. [ * 2]
L. H. Loomis, An Introduction to Abstract Harmonic Analysis , D. van Nostrand Company, Inc. 1953. [ * 3]
H. Lebesgue, Oeuvres Scientifiques , L'Enseignement Mathématique, 1972
M. E. Munroe, Introduction to Measure and Integration , Addison Wesley, 1953. [ * 4]
W. Rudin, Principles of Mathematical Analysis Third edition, McGraw Hill, 1976. [ * 5]
W. Rudin, Real and Complex Analysis , McGraw Hill, 1966. [ * 6]
^ Very thorough treatment, particularly for probabilists with good notes and historical references.
^ A classic, though somewhat dated presentation.
^ Includes a presentation of the Daniell integral.
^ Good treatment of the theory of outer measures.
^ Known as Little Rudin , contains the basics of the Lebesgue theory, but does not treat material such as Fubini's theorem .
^ Known as Big Rudin . A complete and careful presentation of the theory. Good presentation of the Riesz extension theorems. However, there is a minor flaw (in the first edition) in the proof of one of the extension theorems, the discovery of which constitutes exercise 21 of Chapter 2.






![{\displaystyle \int _{[0,1]}1_{\mathbf {Q} }\,d\mu =\mu (\mathbf {Q} \cap [0,1])=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa27280365d1ce3ef8f8adeee1fc7a77fed4db8b)












![{\displaystyle (a,+\infty ]=(a,+\infty )\cup \{+\infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cd72cb6118b345090b99a56c06b7cec1539a6b9)
![{\displaystyle f^{-1}((a,\infty ])\in M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f6afd8da64a9f70c85747f84a708ff124b90a29)






















![{\displaystyle \int _{A}f\,d\mu =\int _{[a,b]}f\,d\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f93c75ee746be8e05f0e6317fda8db6c41a068)









