在 ざい 幾何 きか 學 がく 中 なか 五 ご 邊 へん 形 がた 是 ぜ 指 ゆび 有 ゆう 五 ご 條 じょう 邊 あたり 和 わ 五 ご 個 こ 頂點 ちょうてん 的 てき 多邊形 たへんけい 角 かく 和 わ 為 ため 度 ど
五邊形可以分為凸五邊形和非凸五邊形,其中非 ひ 凸 とつ 五 ご 角 かく 星 ほし 最 さい 簡單 かんたん 的 てき 對角線 たいかくせん 連 れん 起 おこり 來 らい 構成 こうせい
正 せい 五 ご 邊 へん 形 がた [ 编辑 ] 正 せい 五 ご 邊 へん 形 がた 是 ぜ 指 ゆび 內角 為 ため 度 ど 是 ぜ 一 いち 種 しゅ 正 せい 多邊形 たへんけい 在 ざい 施 ほどこせ 利 り 符號 ふごう 中 ちゅう 可 か
{
5
}
{\displaystyle \left\{5\right\}}
來 らい 表示 ひょうじ
正 せい 五 ご 邊 へん 形 がた 的 てき 中心 ちゅうしん 角 かく 為 ため 度 ど 具有 ぐゆう 五 ご 個 こ 對稱 たいしょう 軸 じく 旋轉 せんてん 對稱 たいしょう 性 せい 有 ゆう 個 こ 階 かい 和 わ
高 こう
=
5
+
2
5
2
⋅
{\displaystyle ={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}\cdot }
邊 あたり 長 ちょう
≈
1.539
⋅
{\displaystyle \approx 1.539\cdot }
邊 あたり 長 ちょう 寬 ひろし
=
1
+
5
2
⋅
{\displaystyle ={\frac {1+{\sqrt {5}}}{2}}\cdot }
邊 あたり 長 ちょう
≈
1.618
⋅
{\displaystyle \approx 1.618\cdot }
邊 あたり 長 ちょう 對角線 たいかくせん 長 ちょう
=
R
5
+
5
2
=
2
R
cos
18
∘
=
2
R
cos
π ぱい 10
≈
1.902
R
,
{\displaystyle =R\ {\sqrt {\frac {5+{\sqrt {5}}}{2}}}=2R\cos 18^{\circ }=2R\cos {\frac {\pi }{10}}\approx 1.902R,}
其中
R
{\displaystyle R}
為 ため 外接 がいせつ 圓 えん 半徑 はんけい
邊 あたり 長 ちょう 為 ため
t
{\displaystyle t}
的 てき 正 せい 凸 とつ 個 こ 等 とう 腰 こし 三角形 さんかっけい 計算 けいさん
A
=
t
2
25
+
10
5
4
=
5
t
2
tan
(
54
∘
)
4
≈
1.720
t
2
.
{\displaystyle A={\frac {t^{2}{\sqrt {25+10{\sqrt {5}}}}}{4}}={\frac {5t^{2}\tan(54^{\circ })}{4}}\approx 1.720t^{2}.}
正 せい 因 いん 為 ため 角 かく 是 ぜ 不能 ふのう 整除 せいじょ 年 ねん (2015-Missing required parameter 1=month ! ) [update] 年 ねん 月 がつ 里 さと 昂 のぼる 高等 こうとう 学校 がっこう 宣 せん 称 しょう 已 やめ 只 ただ 存在 そんざい [1]
面積 めんせき 公式 こうしき [ 编辑 ] 正 せい 多邊形 たへんけい 的 てき 面積 めんせき 公式 こうしき 為 ため
A
=
1
2
P
r
{\displaystyle A={\frac {1}{2}}Pr}
其中,
P
{\displaystyle P}
是 これ 周 しゅう 長 ちょう
r
{\displaystyle r}
是 これ 邊 あたり 心 こころ 正 せい 五 ご 邊 へん 形 がた 的 てき
P
{\displaystyle P}
和 わ
r
{\displaystyle r}
可 か 由 ゆかり 三角 さんかく 函數 かんすう 計算 けいさん
A
=
1
2
×
5
t
×
t
tan
(
54
∘
)
2
=
5
t
2
tan
(
54
∘
)
4
{\displaystyle A={\frac {1}{2}}\times 5t\times {\frac {t\tan(54^{\circ })}{2}}={\frac {5t^{2}\tan(54^{\circ })}{4}}}
其中,
t
{\displaystyle t}
是正 ぜせい 五 ご 邊 へん 形 がた 的 てき 邊 あたり 長 ちょう
內切圓 えん 半徑 はんけい [ 编辑 ] 正 せい 五 ご 邊 へん 形 がた 是 ぜ 一 いち 個 こ 圓 えん 外切 がいせつ 多邊形 たへんけい 因 いん 內切圓 えん 。其內切 きり 圓 えん 半徑 はんけい 與 あずか 邊 あたり 心 こころ 相 あい 同 どう 並 なみ 長 ちょう 來 らい 決定 けってい
r
=
t
2
tan
(
π ぱい
/
5
)
=
t
2
5
−
20
≈
0.6882
⋅
t
{\displaystyle r={\frac {t}{2\tan(\pi /5)}}={\frac {t}{2{\sqrt {5-{\sqrt {20}}}}}}\approx 0.6882\cdot t}
其中,
r
{\displaystyle r}
為 ため 圓 えん 半徑 はんけい 與 あずか 邊 あたり 心 こころ 相 あい 同 どう 為 ため 正 せい 五 ご 邊 へん 形 がた 邊 あたり 長 ちょう
構造 こうぞう [ 编辑 ] 里 さと 士 し 滿 まん 提出 ていしゅつ 了 りょう 一 いち 個 こ 構造 こうぞう 正 せい 五 ご 邊 へん 形 がた 的 てき 方法 ほうほう [2] 並 なみ 克 かつ 倫 りん 威 い 爾 なんじ 的 てき 多面體 ためんたい 中 ちゅう 被 ひ 進一 しんいち 步 ふ 討論 とうろん [3]
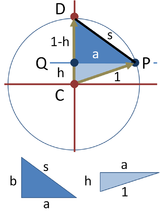
右上 みぎうえ 的 てき 圖 ず 顯示 けんじ 了 りょう 里 さと 士 し 滿 まん 繪 え 製 せい 正 せい 五 ご 邊 へん 形 がた 的 てき 方法 ほうほう 先 さき 利用 りよう 單位 たんい 圓 えん 決定 けってい 五 ご 邊 へん 形 がた 的 てき 半徑 はんけい
C
{\displaystyle C}
為 ため 單位 たんい 圓 えん 圓心 えんしん
M
{\displaystyle M}
是 これ 圓 えん
C
{\displaystyle C}
半徑 はんけい 的中 てきちゅう 點 てん
D
{\displaystyle D}
是 ぜ 位 い 直 ちょく
M
C
{\displaystyle MC}
的 てき 一 いち 條 じょう 半徑 はんけい 的 てき 圓周 えんしゅう 上 じょう 作 さく
∠
C
M
D
{\displaystyle \angle CMD}
的 まと 角 かく 平分 へいぶん 線 せん 令 れい
Q
{\displaystyle Q}
為 ため
∠
C
M
D
{\displaystyle \angle CMD}
的 まと 角 かく 平分 へいぶん 線 せん 與 あずか
C
D
{\displaystyle CD}
的 てき 交點 こうてん 作 さく 過 か
Q
{\displaystyle Q}
平行 へいこう
M
C
{\displaystyle MC}
的 てき 直線 ちょくせん 令 れい 之 の 與 あずか 圓 えん
C
{\displaystyle C}
相 あい 交點 こうてん 為 ため
P
{\displaystyle P}
則 のり
D
P
{\displaystyle DP}
為 ため 正 せい 五 ご 邊 へん 形 がた 的 てき 邊 あたり 長 ちょう
這條邊 べ 的 てき 長 ちょう 度 ど 可 か 利用 りよう 圓 えん 下方 かほう 的 てき 兩個 りゃんこ 直角 ちょっかく 三角形 さんかっけい
D
C
M
{\displaystyle DCM}
和 わ
Q
C
M
{\displaystyle QCM}
利用 りよう 定理 ていり 的 てき 三角形 さんかっけい 斜邊 しゃへん 為 ため
5
2
{\displaystyle {\frac {\sqrt {5}}{2}}\scriptstyle }
小 しょう 三角形 さんかっけい 一 いち 股 また h 可 か 由 ゆかり 半角 はんかく 公式 こうしき 求 もとめ 得 え
tan
(
ϕ
/
2
)
=
1
−
cos
(
ϕ
)
sin
(
ϕ
)
,
{\displaystyle \tan(\phi /2)={\frac {1-\cos(\phi )}{\sin(\phi )}}\ ,}
其中,角 かく
ϕ
{\displaystyle \phi }
可 か 由 ゆかり 大 だい 三角形 さんかっけい 求 もとめ 得 え 為 ため
h
=
5
−
1
4
.
{\displaystyle h={\frac {{\sqrt {5}}-1}{4}}\ .}
由 よし 得 え 到 いた 在 ざい 下圖 したず 正 せい 右側 みぎがわ 三角形 さんかっけい 的 てき 邊 あたり 長 ちょう
a
{\displaystyle a}
可 か 再 さい 帶 おび 一 いち 次 じ 定理 ていり 得 とく
a
2
=
1
−
h
2
;
a
=
1
2
5
+
5
2
.
{\displaystyle a^{2}=1-h^{2}\ ;\ a={\frac {1}{2}}{\sqrt {\frac {5+{\sqrt {5}}}{2}}}\ .}
欲求 よっきゅう 出 で 五 ご 邊 へん 形 がた 邊 あたり 長 ちょう
s
{\displaystyle s}
可 か 透過 とうか 左側 ひだりがわ 的 てき 三角形 さんかっけい 由 ゆかり 定理 ていり 得 とく
s
2
=
(
1
−
h
)
2
+
a
2
=
(
1
−
h
)
2
+
1
−
h
2
=
1
−
2
h
+
h
2
+
1
−
h
2
=
2
−
2
h
=
2
−
2
(
5
−
1
4
)
{\displaystyle s^{2}=(1-h)^{2}+a^{2}=(1-h)^{2}+1-h^{2}=1-2h+h^{2}+1-h^{2}=2-2h=2-2\left({\frac {{\sqrt {5}}-1}{4}}\right)\ }
=
5
−
5
2
.
{\displaystyle ={\frac {5-{\sqrt {5}}}{2}}\ .}
使用 しよう 圓 えん 規 ぶんまわし 與 あずか 直 ちょく 尺 せき 建 けん 正 せい 五 ご 邊 へん 形 がた 五 ご 邊 へん 形 がた 邊 あたり 長 ちょう
s
{\displaystyle s}
為 ため
s
=
5
−
5
2
,
{\displaystyle s={\sqrt {\frac {5-{\sqrt {5}}}{2}}}\ ,}
得 え 到 いた 了 りょう 正確 せいかく 的 てき 結果 けっか [4] 因 いん 種 しゅ 構造 こうぞう 正 せい 五 ご 邊 へん 形 がた 的 てき 方法 ほうほう 是 ぜ 有效 ゆうこう 的 てき
約 やく 西元 にしもと 前 ぜん 年 ねん 欧 おう 得 とく 在 ざい 他 た 的 てき 几何原本 げんぽん 》中 ちゅう 了 りょう 一 いち 直 ちょく 尺 せき 和 かず 正 せい 五 ご 的 てき
物理 ぶつり 方法 ほうほう [ 编辑 ] 打 だ 一 いち 個 こ 反 はん 手結 たゆ 的 まと 長 ちょう 條 じょう 紙 し 張 ちょう 正 せい 反 はん 手結 たゆ 並 なみ 將 はた 多 た 出來 でき 的 てき 部分 ぶぶん 向後 こうご 折 おり 來 らい 構造 こうぞう 折 おり 法被 はっぴ 用 よう 在 ざい 摺 すり 紙 し 星 ほし 星 ぼし 上 じょう
等邊 とうへん 五 ご 邊 へん 形 がた [ 编辑 ] 有 ゆう 兩個 りゃんこ 直角 ちょっかく 的 てき 等邊 とうへん 五 ご 邊 へん 形 がた 等邊 とうへん 等邊 とうへん 五 ご 邊 へん 形 がた 不 ふ 一定 いってい 是正 ぜせい 五 ご 邊 へん 形 がた 由 よし 可 か 自 じ 一 いち 個 こ 範圍 はんい 集合 しゅうごう 形成 けいせい 一 いち 個 こ 等邊 とうへん 五 ご 邊 へん 形 がた 的 てき 群 ぐん 相 そう 比 ひ 之 の 下 した 正 せい 五 ご 邊 へん 形 がた 由 よし 內角 也固定 こてい 了 りょう 因 いん 唯一 ゆいいつ 的 てき
有 ゆう 兩個 りゃんこ 直角 ちょっかく 的 てき 等邊 とうへん 因 いん 常用 じょうよう 作 さく 房子 ふさこ 的 てき 符號 ふごう
五 ご 邊 へん 形 がた [ 编辑 ] 五 ご 邊 へん 形 がた 是 ぜ 指 ゆび 用 よう 全 ちょん 等 ひとし 的 てき 五 ご 邊 へん 形 がた 沒 ぼつ 有 ゆう 空隙 くうげき 地 ち 填 はま 滿 まん 整 せい 個 こ 平面 へいめん 的 てき 鑲嵌 圖形 ずけい 年 ねん 月 がつ 里 さと 昂 のぼる 高等 こうとう 学校 がっこう 宣 せん 称 しょう 已 やめ 只 ただ 存在 そんざい [1]
扭歪五 ご 邊 へん 形 がた [ 编辑 ] 塗 ぬり 上 じょう 黃色 おうしょく 的 てき 邊 あたり 是 ぜ 一 いち 個 こ 五 ご 邊 へん 形 がた 位 い 正 せい 五 ご 的 てき 施 ほどこせ 爾 なんじ 圖 ず 的 てき 透視 とうし 投影 とうえい 扭歪五 ご 邊 へん 形 がた 又 また 稱 たたえ 不 ふ 共 とも 面 めん 五 ご 邊 へん 形 がた 是 ぜ 指 ゆび 頂點 ちょうてん 並 なみ 非 ひ 完全 かんぜん 共 とも 面 めん 的 てき 五 ご 邊 へん 形 がた
皮 かわ 特 とく 里 さと 多邊形 たへんけい [ 编辑 ] 一些高維度多胞體的皮 かわ 特 とく 里 さと 多邊形 たへんけい 是 ぜ 五 ご 邊 へん 形 がた 例 れい 四 よん 正 せい 五 ご [5]
類 るい 五 ご 邊 へん 形 がた 形 がた [ 编辑 ] 類 るい 只 ただ 存在 そんざい 四 よん 或 ある 以下 いか 的 てき 空間 くうかん 形狀 けいじょう 都 と 具有 ぐゆう n 的 てき 考 こう 克 かつ 群 ぐん [6] [7] [8] 中正 ちゅうせい 五 ご 邊 へん 形 がた 為 ため 2 階數 かいすう 為 ため
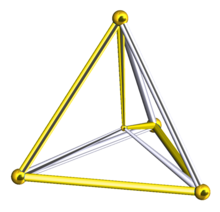
由 よし 五 ご 邊 へん 形 がた 組成 そせい 的 てき 多面體 ためんたい [ 编辑 ] 有 ゆう 最 さい 常見 つねみ 的 てき 是正 ぜせい 十 じゅう 二 に 面體 めんてい 是 ぜ
参考 さんこう 文献 ぶんけん [ 编辑 ]
^ 1.0 1.1 Exhaustive search of convex pentagons which tile the plane (PDF) . [2019-07-29 ] . (原始 げんし 内容 ないよう 存 そん (PDF) 于2020-11-12). ^ Herbert W Richmond. Pentagon . 1893 [2016-08-28 ] . (原始 げんし 内容 ないよう 存 そん ^ Peter R. Cromwell. Polyhedra . : 63 [2016-08-28 ] . ISBN 0-521-66405-5原始 げんし 内容 ないよう 存 そん ^ This result agrees with Herbert Edwin Hawkes; William Arthur Luby; Frank Charles Touton. Exercise 175. Plane geometry . Ginn & Co. 1920: 302 [2016-08-28 ] . (原始 げんし 内容 ないよう 存 そん
^ H.S.M. Coxeter Regular Polytopes
^ Kaleidoscopes: Selected Writings of H.S.M. Coxeter , edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (页面存 そん ,存 そん 互联网档案 あん )^ (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α あるふぁ β べーた γ がんま [Elemente der Mathematik 44 (2) (1989) 25–36]
^ Coxeter, Regular Polytopes , 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Table I(ii): 16 regular polytopes {p, q, r} in four dimensions, pp. 292–293)
参 まいり [ 编辑 ]