ウィキブックスに
ベクトル空間 くうかん 関連 かんれん の
解説 かいせつ 書 しょ ・
教科書 きょうかしょ があります。
数学 すうがく 特 とく 線型 せんけい 代数 だいすう 学 がく ベクトル空間 くうかん (ベクトルくうかん、英 えい vector space 線型 せんけい 空間 くうかん 英 えい linear space ベクトル (英 えい vector 呼 よ 元 もと 集 あつ 成 な 数学 すうがく 的 てき 構造 こうぞう
ベクトルには和 わ (wikidata ) 定義 ていぎ スカラー と呼 よ 数 かず 積 せき 乗法 じょうほう 行 おこな 実数 じっすう 多 おお 複素数 ふくそすう 有理数 ゆうりすう 一般 いっぱん 可 か 換 かわ 体 からだ 元 もと 乗法 じょうほう 持 も 空間 くうかん 和 わ 乗法 じょうほう 演算 えんざん 空間 くうかん 公理 こうり 呼 よ 特定 とくてい 条件 じょうけん #定義 ていぎ 節 ふし 参照 さんしょう 満足 まんぞく 空間 くうかん 一 ひと 例 れい 力 ちから 物理 ぶつり 量 りょう 表現 ひょうげん 用 もち 空間 くうかん 全体 ぜんたい 同 おな 種類 しゅるい 任意 にんい 二 ふた 力 ちから 加 くわ 合 あ 力 ちから 合成 ごうせい 呼 よ 第 だい 三 さん 力 ちから 与 あた 力 ちから 実 じつ 数 すう 倍 ばい 別 べつ 力 ちから 表 あらわ 同 おな 調子 ちょうし 平面 へいめん 空間 くうかん 変位 へんい 表 あらわ 全体 ぜんたい 空間 くうかん 成 な
ベクトル空間 くうかん 線型 せんけい 代数 だいすう 学 がく 主題 しゅだい 空間 くうかん 次元 じげん 大雑把 おおざっぱ 空間 くうかん 独立 どくりつ 方向 ほうこう 数 かず 決 き 特徴 とくちょう 空間 くうかん ノルム や内積 ないせき 追加 ついか 構造 こうぞう 持 も 空間 くうかん 解析 かいせき 学 がく 主 おも 関数 かんすう 無限 むげん 次元 じげん 関数 かんすう 空間 くうかん 形 かたち 自然 しぜん 生 しょう 解析 かいせき 学 がく 的 てき 問題 もんだい 列 れつ 与 あた 収束 しゅうそく 否 ひ 決定 けってい 空 そら 傍 はた 間 あいだ 追加 ついか 構造 こうぞう 考 かんが 実現 じつげん 空間 くうかん 適当 てきとう 位相 いそう 空間 くうかん 備 そな 近傍 きんぼう 連続 れんぞく 考 かんが 線型 せんけい 位相 いそう 空間 くうかん 特 とく バナッハ空間 くうかん やヒルベルト空間 くうかん については、豊 ゆた 理論 りろん 存在 そんざい
歴史 れきし 的 てき 視点 してん 空間 くうかん 概念 がいねん 萌芽 ほうが 世紀 せいき 解析 かいせき 幾何 きか 学 がく 行列 ぎょうれつ 線型 せんけい 方程式 ほうていしき 系 けい 理論 りろん 概念 がいねん 遡 さかのぼ 現代 げんだい 的 てき 抽象 ちゅうしょう 的 てき 取扱 とりあつか 初 はじ 定式 ていしき 化 か 世紀 せいき 後半 こうはん ペアノ によるもので、それはユークリッド空間 くうかん 一般 いっぱん 対象 たいしょう 範疇 はんちゅう 含 ふく 理論 りろん 大半 たいはん 直線 ちょくせん 平面 へいめん 高 こう 次元 じげん 対応 たいおう 物 ぶつ 古典 こてん 的 てき 幾何 きか 学 がく 的 てき 概念 がいねん 拡張 かくちょう 割 さ
今日 きょう 空間 くうかん 数学 すうがく 科学 かがく 工学 こうがく 広 ひろ 応用 おうよう 空間 くうかん 線型 せんけい 方程式 ほうていしき 系 けい 扱 あつか 適当 てきとう 概念 がいねん 例 たと 画像 がぞう 圧縮 あっしゅく 使 つか フーリエ級数 きゅうすう のための枠組 わくぐ 提示 ていじ 偏 へん 微分 びぶん 方程式 ほうていしき 解法 かいほう 用 もち 環境 かんきょう 提供 ていきょう テンソル のような幾何 きか 学 がく 的 てき 物理 ぶつり 学 がく 的 てき 対象 たいしょう 抽象 ちゅうしょう 的 てき 座標 ざひょう 依 よ 英 えい coordinate-free ) で扱 あつか 方法 ほうほう 与 あた 線型 せんけい 化 か 手法 しゅほう 用 もち 多様 たよう 体 たい 局所 きょくしょ 的 てき 性質 せいしつ 説明 せつめい
ベクトル空間 くうかん 概念 がいねん 様々 さまざま 方法 ほうほう 一般 いっぱん 化 か 幾何 きか 学 がく 抽象 ちゅうしょう 代 だい 数学 すうがく 進 すす 概念 がいねん 導 みちび
ベクトル空間 くうかん 概念 がいねん 特定 とくてい 二 ふた 場合 ばあい 例 れい 簡単 かんたん 内容 ないよう 説明 せつめい
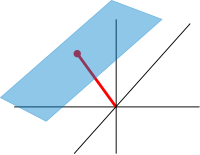
平面 へいめん 上 じょう 有向 ゆうこう 線分 せんぶん [ 編集 へんしゅう ] ベクトル空間 くうかん 簡単 かんたん 例 れい 一 ひと 平面 へいめん 上 うえ 固定 こてい 点 てん 始点 してん 矢印 やじるし 有向 ゆうこう 線分 せんぶん 全 すべ 成 な 集合 しゅうごう 与 あた 物理 ぶつり 学 がく 力 ちから 速度 そくど 記述 きじゅつ 有向 ゆうこう 線分 せんぶん v w 与 あた 二 ふた 有向 ゆうこう 線分 せんぶん 張 は 平行四辺形 へいこうしへんけい 対角線 たいかくせん 一 ひと 原点 げんてん 始点 してん 有向 ゆうこう 線分 せんぶん 含 ふく 新 あたら 有向 ゆうこう 線分 せんぶん 二 ふた 有向 ゆうこう 線分 せんぶん 和 わ v w 呼 よ 一 ひと 演算 えんざん 有向 ゆうこう 線分 せんぶん 伸 の 縮 ちぢ スケール因子 いんし )させるもので、任意 にんい 正 せい 実数 じっすう a が与 あた v 向 む 同 おな 長 なが a の分 ぶん 拡大 かくだい 英 えい dilate ) または縮小 しゅくしょう 英 えい shrink ) した有向 ゆうこう 線分 せんぶん v a -倍 ばい av 言 い a が負 まけ av 今度 こんど 逆 ぎゃく 方向 ほうこう 伸 の 縮 ちぢ 同様 どうよう 定 さだ
いくつか実際 じっさい 図示 ずし 例 たと a = 2得 え aw w 同 どう 方向 ほうこう 長 なが w 二 に 倍 ばい 下図 したず 右 みぎ 赤 あか 2w は和 わ w w 等 ひと (−1)v v v 同 おな 長 なが 向 む v 逆 ぎゃく 下図 したず 右 みぎ 青 あお
数 かず 順序 じゅんじょ 対 たい [ 編集 へんしゅう ] もう一 ひと 重要 じゅうよう 例 れい 実数 じっすう x , y 対 たい 与 あた x と y の対 たい 並 なら 順番 じゅんばん 重要 じゅうよう 対 たい 順序 じゅんじょ 対 たい 対 たい (x , y ) と書 か 対 たい 和 わ 実 じつ 数 すう 倍 ばい
(x 1 , y 1 ) + (x 2 , y 2 ) = (x 1 + x 2 , y 1 + y 2 ) および
a (x , y ) = (ax , ay )で定義 ていぎ
集合 しゅうごう V が、その上 うえ 二 に 項 こう 演算 えんざん + と、体 からだ F の V への作用 さよう ◦ をもち、これらが任意 にんい u v w V ; a , b ∈ F [nb 1] 関 かん 次 つぎ 公理系 こうりけい 満 み 三 さん 組 くみ (V , +, ◦) は「体 からだ F 上 うえ 空間 くうかん 定義 ていぎ [2]
公理 こうり 条件 じょうけん
加法 かほう 結合 けつごう 律 りつ
u
+
(
v
+
w
)
=
(
u
+
v
)
+
w
{\displaystyle {\boldsymbol {u}}+({\boldsymbol {v}}+{\boldsymbol {w}})=({\boldsymbol {u}}+{\boldsymbol {v}})+{\boldsymbol {w}}}
加法 かほう 可 か 換 かわ 律 りつ
u
+
v
=
v
+
u
{\displaystyle {\boldsymbol {u}}+{\boldsymbol {v}}={\boldsymbol {v}}+{\boldsymbol {u}}}
加法 かほう 単位 たんい 元 もと 存在 そんざい 零 れい
0
∈
V
{\displaystyle {\boldsymbol {0}}\in V}
存在 そんざい 任意 にんい
v
∈
V
{\displaystyle {\boldsymbol {v}}\in V}
対 たい
v
+
0
=
v
{\displaystyle {\boldsymbol {v}}+{\boldsymbol {0}}={\boldsymbol {v}}}
満 み
加法 かほう 逆 ぎゃく 元 もと 存在 そんざい 任意 にんい
v
∈
V
{\displaystyle {\boldsymbol {v}}\in V}
対 たい 加法 かほう 逆 ぎゃく 元 もと
−
v
∈
V
{\displaystyle -{\boldsymbol {v}}\in V}
存在 そんざい
v
+
(
−
v
)
=
0
{\displaystyle {\boldsymbol {v}}+(-{\boldsymbol {v}})={\boldsymbol {0}}}
加法 かほう 対 たい 乗法 じょうほう 分配 ぶんぱい 律 りつ
a
(
u
+
v
)
=
a
u
+
a
v
{\displaystyle a({\boldsymbol {u}}+{\boldsymbol {v}})=a{\boldsymbol {u}}+a{\boldsymbol {v}}}
体 からだ 加法 かほう 対 たい 乗法 じょうほう 分配 ぶんぱい 律 りつ
(
a
+
b
)
v
=
a
v
+
b
v
{\displaystyle (a+b){\boldsymbol {v}}=a{\boldsymbol {v}}+b{\boldsymbol {v}}}
体 からだ 乗法 じょうほう 乗法 じょうほう 両立 りょうりつ 条件 じょうけん
a
(
b
v
)
=
(
a
b
)
v
{\displaystyle a(b{\boldsymbol {v}})=(ab){\boldsymbol {v}}}
[nb 2]
スカラーの乗法 じょうほう 単位 たんい 元 もと 存在 そんざい
1
v
=
v
{\displaystyle 1{\boldsymbol {v}}={\boldsymbol {v}}}
左辺 さへん 1 は F の乗法 じょうほう 単位 たんい 元 もと
ベクトル空間 くうかん 要素 ようそ 次 じ 呼 よ
体 からだ F : 係数 けいすう 体 たい 英 えい coefficient field, scalar field )V の元 もと ベクトル (英 えい vector )F の元 もと スカラー (英 えい scalar ) あるいは 係数 けいすう 英 えい coefficient )二 に 項 こう 演算 えんざん +: V × V → V ; (v w v w : 加法 かほう 作用 さよう ◦: F × V → V ; (a , v av : スカラー乗法 じょうほう 公理系 こうりけい ベクトル空間 くうかん 公理 こうり 系 けい 導入 どうにゅう 節 ぶし 始点 してん 固定 こてい 有向 ゆうこう 平面 へいめん 線分 せんぶん 全体 ぜんたい 実数 じっすう 順序 じゅんじょ 対 たい 全体 ぜんたい 成 な 集合 しゅうごう 空間 くうかん 例 れい 挙 あ 実数 じっすう 体 たい 実数 じっすう 全体 ぜんたい 体 からだ 上 じょう 空間 くうかん 公理系 こうりけい 性質 せいしつ 一般 いっぱん 化 か 実際 じっさい 二 に 番目 ばんめ 例 れい 二 ふた 順序 じゅんじょ 対 たい 和 わ 和 わ 順番 じゅんばん 依 よ
(x v y v x w y w x w y w x v y v を満 み 有向 ゆうこう 線分 せんぶん 例 れい v w w v 和 わ 定義 ていぎ 平行四辺形 へいこうしへんけい 和 わ 順番 じゅんばん 依存 いぞん 言 い 他 た 公理 こうり 同様 どうよう 方法 ほうほう 満 み 例 れい 故 ゆえ 特定 とくてい 種類 しゅるい 持 も 具体 ぐたい 的 てき 特質 とくしつ 無視 むし 定義 ていぎ 先 さき 二 ふた 例 れい 空間 くうかん 一 ひと 概念 がいねん 扱 あつか
ベクトル空間 くうかん 係数 けいすう 体 たい 種類 しゅるい 基 もと 次 じ 呼 よ
実 じつ 空間 くうかん 英 えい real vector space 実数 じっすう 体 からだ R 複素 ふくそ 空間 くうかん 英 えい complex vector space 複素数 ふくそすう 体 からだ C F -ベクトル空間 くうかん 英 えい F -vector space F 上 うえ 空間 くうかん 英 えい vector space over F 任意 にんい 体 からだ F 体 からだ 本質 ほんしつ 的 てき 四則 しそく 演算 えんざん 自由 じゆう 数 かず 集合 しゅうごう [nb 3] 例 たと 有理数 ゆうりすう 全体 ぜんたい Q 体 からだ 成 な
平面 へいめん 高次 こうじ 空間 くうかん 直観 ちょっかん 的 てき 近 ちか 角度 かくど 距離 きょり 概念 がいねん 存在 そんざい 一般 いっぱん 的 てき 空間 くうかん 概念 がいねん 不要 ふよう 実際 じっさい 存在 そんざい 空間 くうかん 概念 がいねん 一般 いっぱん 的 てき 空間 くうかん 追加 ついか 的 てき 定義 ていぎ 構造 こうぞう #付加 ふか 構造 こうぞう 備 そな 空間 くうかん )。
別 べつ 定式 ていしき 化 か 初等 しょとう 的 てき 帰結 きけつ [ 編集 へんしゅう ] ベクトルの加法 かほう 乗法 じょうほう 二 に 項 こう 演算 えんざん 定義 ていぎ 閉性 と呼 よ 性質 せいしつ 満 み V の各 かく 元 もと u v F の各 かく 元 もと a に対 たい u v av 必 かなら V に属 ぞく 空間 くうかん 公理 こうり 独立 どくりつ 条件 じょうけん 加 くわ 文献 ぶんけん
抽象 ちゅうしょう 代 だい 数学 すうがく 言葉 ことば 言 い 先 さき 公理系 こうりけい 最初 さいしょ 四 よっ 全体 ぜんたい 加法 かほう 関 かん アーベル群 ぐん を成 な 条件 じょうけん 残 のこ 条件 じょうけん 群 ぐん F 上 うえ 加 か 群 ぐん となる」という条件 じょうけん 体 からだ F からベクトル全体 ぜんたい 成 な 群 ぐん 自己 じこ 準 じゅん 同型 どうけい 環 たまき 環 かん 準 じゅん 同型 どうけい f が存在 そんざい 換 いか 場合 ばあい 乗法 じょうほう av ≔ (f (a ))(v 定 さだ [4]
ベクトル空間 くうかん 公理系 こうりけい 直接的 ちょくせつてき 分 わ 群論 ぐんろん 全体 ぜんたい 成 な 加法 かほう 群 ぐん 適用 てきよう 得 え 例 たと V の零 れい 0 各 かく 元 もと v 加法 かほう 逆 ぎゃく 元 もと −v が一意 いちい 存在 そんざい 方法 ほうほう 得 え 性質 せいしつ 分配 ぶんぱい 法則 ほうそく 来 く 例 たと av = 0 ⇔ a = 0v 0
ベクトル空間 くうかん 平面 へいめん 空間 くうかん 座標 ざひょう 系 けい 導入 どうにゅう 通 つう アフィン空間 くうかん から生 しょう 年 ねん ルネ・デカルト とピエール・ド・フェルマー は、二 に 変数 へんすう 方程式 ほうていしき 解 かい 平面 へいめん 曲線 きょくせん 上 うえ 点 てん 等化 とうか 解析 かいせき 幾何 きか 学 がく 発見 はっけん 座標 ざひょう 用 もち 幾何 きか 学 がく 的 てき 解 かい 到達 とうたつ ベルナルト・ボルツァーノ は1804年 ねん 点 てん 同士 どうし 点 てん 直線 ちょくせん 間 あいだ 演算 えんざん 導入 どうにゅう 前身 ぜんしん 概念 がいねん 研究 けんきゅう アウグスト・フェルディナント・メビウス が1827年 ねん 提唱 ていしょう 重心 じゅうしん 座標 ざひょう 系 けい (英語 えいご 版 ばん 英 えい barycentric coordinates ) の概念 がいねん 用 もち 構築 こうちく 定義 ていぎ 基礎 きそ ジュスト・ベラヴィティス (英語 えいご 版 ばん 双 そう 点 てん 英 えい bipoint ) の概念 がいねん 一方 いっぽう 端点 たんてん 始点 してん 他方 たほう 端点 たんてん 終点 しゅうてん 有向 ゆうこう 線分 せんぶん ジャン=ロベール・アルガン (英語 えいご 版 ばん ウィリアム・ローワン・ハミルトン により複素数 ふくそすう 表現 ひょうげん 見直 みなお 後 ご 四 よん 元 げん 数 すう 双 そう 四 よん 元 げん 数 すう (英語 えいご 版 ばん 概念 がいねん 繋 つな 数 かず R 2 , R 4 , R 8 元 もと 対 たい 線型 せんけい 結合 けつごう 用 もち 取扱 とりあつか 年 ねん エドモンド・ラゲール (彼 かれ 線型 せんけい 方程式 ほうていしき 系 けい 定義 ていぎ 遡 さかのぼ
1857年 ねん アーサー・ケイリー は、線型 せんけい 写像 しゃぞう 馴染 なじ 記述 きじゅつ 簡素 かんそ 化 か 行列 ぎょうれつ 導入 どうにゅう 同 おな 頃 ごろ ヘルマン・グラスマン はメビウスの「重心 じゅうしん 計算 けいさん 英 えい the barycentric calculus ) を研究 けんきゅう 算法 さんぽう 伴 ともな 抽象 ちゅうしょう 的 てき 対象 たいしょう 成 な 集合 しゅうごう 構想 こうそう 研究 けんきゅう 線型 せんけい 独立 どくりつ 次元 じげん ドット積 せき などの概念 がいねん 含 ふく 実際 じっさい 年 ねん 考案 こうあん 乗法 じょうほう 空間 くうかん 枠組 わくぐ 推 お 進 すす 今日 きょう 体 からだ 上 じょう 多元 たげん 環 たまき 呼 よ 概念 がいねん 到達 とうたつ ジュゼッペ・ペアノ はベクトル空間 くうかん 線型 せんけい 写像 しゃぞう 現代 げんだい 的 てき 定義 ていぎ 与 あた 最初 さいしょ 人 ひと 年 ねん
ベクトル空間 くうかん 重要 じゅうよう 発展 はってん アンリ・ルベーグ による函数 かんすう 空間 くうかん 構成 こうせい 起 お 後 ご 年 ねん ステファン・バナフ とダフィット・ヒルベルト によって定式 ていしき 化 か 当時 とうじ 代数 だいすう 学 がく 新 あたら 研究 けんきゅう 分野 ぶんや 関数 かんすう 解析 かいせき 学 がく 相互 そうご 影響 えいきょう 始 はじ p -乗 の 可 か 積分 せきぶん 函数 かんすう 空間 くうかん Lp ヒルベルト空間 くうかん などの重要 じゅうよう 概念 がいねん 生 う 出 だ [12] 無限 むげん 次元 じげん 場合 ばあい 含 ふく 空間 くうかん 概念 がいねん 堅 かた 確立 かくりつ 多 おお 数学 すうがく 分野 ぶんや 用 もち 始 はじ
数 かず 空間 くうかん [ 編集 へんしゅう ] 体 からだ F 上 うえ 空間 くうかん 簡単 かんたん 例 れい 体 からだ F 自身 じしん 標準 ひょうじゅん 的 てき 加法 かほう 乗法 じょうほう 考 かんが Fn と書 か 数 かず 空間 くうかん 英 えい coordinate space n = 1場合 ばあい 数 すう 空間 くうかん 元 もと n (長 なが n の数列 すうれつ
(
a
1
,
a
2
,
…
,
a
n
)
{\displaystyle (a_{1},a_{2},\dotsc ,a_{n})}
で、各 かく ai が F の元 もと F = R n = 2場合 ばあい 上記 じょうき #導入 どうにゅう 節 ふし 論 ろん
複素数 ふくそすう 全体 ぜんたい 成 な 集合 しゅうごう C 実数 じっすう x , y 用 もち x + iy 形 かたち 表 あらわ 数 かず
i
=
−
1
{\textstyle i={\sqrt {-1}}}
虚数 きょすう 単位 たんい 全体 ぜんたい x , y , a , b , c 何 いず 実数 じっすう 通常 つうじょう 和 わ (x + iy ) + (a + ib ) = (x + a ) + i (y + b ) と実 じつ 数 すう 倍 ばい c (x + iy ) = (cx ) + i (cy )実数 じっすう 体 たい 上 じょう 空間 くうかん 空間 くうかん 公理 こうり 複素数 ふくそすう 算術 さんじゅつ 同 おな 規則 きそく 満足 まんぞく 事実 じじつ 従 したが
実 じつ 複素数 ふくそすう 体 たい 例 れい 本質 ほんしつ 的 てき 同型 どうけい 意味 いみ 導入 どうにゅう 節 ぶし 挙 あ 実数 じっすう 順序 じゅんじょ 対 たい 成 な 空間 くうかん 例 れい 同 おな 即 すなわ 複素数 ふくそすう x + iy 複素 ふくそ 平面 へいめん 順序 じゅんじょ 対 たい (x , y ) を表 あらわ 考 かんが 複素数 ふくそすう 体 たい 和 わ 積 せき 規則 きそく 先 さき 例 れい 対応 たいおう 理解 りかい
より一般 いっぱん 代数 だいすう 学 がく 代数 だいすう 的 てき 整数 せいすう 論 ろん 体 からだ 拡大 かくだい 空間 くうかん 例 れい 一類 いちるい 与 あた 即 すなわ 体 からだ F を部分 ぶぶん 体 たい 含 ふく 体 からだ E は、E 加法 かほう F の元 もと E における乗法 じょうほう 関 かん F -ベクトル空間 くうかん 例 たと 複素数 ふくそすう 体 たい R 上 うえ 空間 くうかん 拡大 かくだい 体 たい
Q
(
5
)
{\textstyle \mathbf {Q} ({\sqrt {5}})}
Q 上 うえ 空間 くうかん 特 とく 数 かず 論 ろん 的 てき 意味 いみ 例 れい 有理数 ゆうりすう 体 たい Q 一 ひと 代数 だいすう 的 てき 複素数 ふくそすう α あるふぁ 添加 てんか 拡大 かくだい 代数 だいすう 体 たい Q (α あるふぁ Q (α あるふぁ Q α あるふぁ 含 ふく 最小 さいしょう 体 からだ
任意 にんい 一 ひと 集合 しゅうごう Ω おめが 体 からだ F への函数 かんすう 全体 ぜんたい 点 てん 和 わ 倍 ばい 空間 くうかん 成 な 即 すなわ 二 ふた 函数 かんすう f , g 和 わ (f + g ) は
(
f
+
g
)
(
w
)
=
f
(
w
)
+
g
(
w
)
{\displaystyle (f+g)(w)=f(w)+g(w)}
で定義 ていぎ 函数 かんすう 倍 ばい 同様 どうよう 函数 かんすう 空間 くうかん 多 おお 幾何 きか 学 がく 的 てき 状況 じょうきょう 生 しょう 例 たと Ω おめが 実数 じっすう 直線 ちょくせん R 区間 くかん R 他 ほか 部分 ぶぶん 集合 しゅうごう 位相 いそう 空間 くうかん 論 ろん 解析 かいせき 学 がく 多 おお 概念 がいねん 例 たと 連続 れんぞく 性 せい 可 か 積分 せきぶん 性 せい 可 か 微分 びぶん 性 せい 線型 せんけい 性 せい 関 かん 振 ふ 舞 ま 即 すなわ 性質 せいしつ 満 み 函数 かんすう 加算 かさん 倍 ばい 同 おな 性質 せいしつ 持 も [15] 従 したが 函数 かんすう 全体 ぜんたい 成 な 集合 しゅうごう 空間 くうかん 成 な 函数 かんすう 空間 くうかん 函数 かんすう 解析 かいせき 学 がく 方法 ほうほう 用 もち 詳 くわ 調 しら #付加 ふか 構造 こうぞう 備 そな 空間 くうかん 節 ふし 参照 さんしょう 代数 だいすう 学 がく 的 てき 制約 せいやく 空間 くうかん 得 え 空間 くうかん F [x ] は多項式 たこうしき 函数 かんすう
f
(
x
)
=
r
0
+
r
1
x
+
⋯
+
r
n
−
1
x
n
−
1
+
r
n
x
n
{\displaystyle f(x)=r_{0}+r_{1}x+\dotsb +r_{n-1}x^{n-1}+r_{n}x^{n}}
(ただし各 かく 係数 けいすう r 0 , ..., rn F の元 もと 全体 ぜんたい 与 あた
線型 せんけい 方程式 ほうていしき 解 かい 空間 くうかん [ 編集 へんしゅう ] 斉 ひとし 次 じ 線型 せんけい 方程式 ほうていしき 系 けい 空間 くうかん 近 ちか 関係 かんけい 例 たと 方程式 ほうていしき 系 けい
a
+
3b
+
c
= 0
4a
+
2b
+
2c
= 0
の解 かい 全体 ぜんたい 任意 にんい a に対 たい a , b = a /2, c = −5a /2三 みっ 組 ぐみ 与 あた 三 み 組 ぐみ 成分 せいぶん 加算 かさん 倍 ばい 同 おな 比 ひ 持 も 三 みっ 変数 へんすう 組 くみ 解 かい 解 かい 全体 ぜんたい 空間 くうかん 成 な 行列 ぎょうれつ 使 つか 上記 じょうき 複数 ふくすう 線型 せんけい 方程式 ほうていしき 簡略 かんりゃく 化 か 一 ひと 方程式 ほうていしき
A
x
=
0
,
A
=
[
1
3
1
4
2
2
]
{\displaystyle A{\boldsymbol {x}}={\boldsymbol {0}},\quad A={\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}}
にすることができる。ここで A は与 あた 方程式 ほうていしき 係数 けいすう 含 ふく 行列 ぎょうれつ x (a , b , c ) Ax 行列 ぎょうれつ 乗法 じょうほう 0 = (0, 0)零 れい 意味 いみ 同様 どうよう 文脈 ぶんみゃく 斉 ひとし 次 じ 線型 せんけい 微分 びぶん 方程式 ほうていしき 解 かい 全体 ぜんたい 空間 くうかん 成 な 例 たと
f
″
(
x
)
+
2
f
′
(
x
)
+
f
(
x
)
=
0
{\displaystyle f''(x)+2f'(x)+f(x)=0}
(1 )
を解 と a , b 任意 にんい 定数 ていすう f (x ) = ae −x + bxe −x 得 え ex は指数 しすう 函数 かんすう
ベクトル空間 くうかん 分類 ぶんるい
有限 ゆうげん 次元 じげん 空間 くうかん 有限 ゆうげん 空間 くうかん 有限 ゆうげん 個 こ 組 くみ 生成 せいせい {0 } である、ベクトル空間 くうかん [18] 無限 むげん 次元 じげん 空間 くうかん 有限 ゆうげん 次元 じげん 空間 くうかん 定義 ていぎ 満 み 空間 くうかん [19] R 2 v 青 あお 異 こと 基底 きてい 表 あらわ R 2 標準 ひょうじゅん 基底 きてい v xe 1 + ye 2 黒 くろ 別 べつ 斜 はす 底 そこ v f 1 + f 2 赤 あか 基底 きてい 簡明 かんめい 方法 ほうほう 空間 くうかん 構造 こうぞう 明 あき 基底 きてい 適当 てきとう 添字 そえじ 集合 しゅうごう 添字 そえじ 付 つ 有限 ゆうげん 無限 むげん 集合 しゅうごう B = {v i i ∈ I 全体 ぜんたい 空間 くうかん 張 は 極小 きょくしょう 言 い 条件 じょうけん 任意 にんい v 基底 きてい 元 もと 有限 ゆうげん 線型 せんけい 結合 けつごう
v
=
a
1
v
i
1
+
a
2
v
i
2
+
⋯
+
a
n
v
i
n
{\displaystyle v=a_{1}{\boldsymbol {v}}_{i_{1}}+a_{2}{\boldsymbol {v}}_{i_{2}}+\dotsb +a_{n}{\boldsymbol {v}}_{i_{n}}}
(ak がスカラーで v ik 基底 きてい B の元 もと (k = 1, ..., n ) 表 あらわ 意味 いみ 極小 きょくしょう 性 せい B が線型 せんけい 独立 どくりつ 性 せい 持 も 集合 しゅうごう 線型 せんけい 独立 どくりつ 何 いず 元 もと 残 のこ 元 もと 線型 せんけい 結合 けつごう 表 あらわ 言 い 方程式 ほうていしき
a
1
v
i
1
+
a
2
v
i
2
+
⋯
+
a
n
v
i
n
=
0
{\displaystyle a_{1}{\boldsymbol {v}}_{i_{1}}+a_{2}{\boldsymbol {v}}_{i_{2}}+\dotsb +a_{n}{\boldsymbol {v}}_{i_{n}}={\boldsymbol {0}}}
が満 み 全 すべ a 1 , ..., an 零 れい 等 ひと 場合 ばあい 限 かぎ 言 い 同 おな 基底 きてい 線型 せんけい 独立 どくりつ 性 せい V の任意 にんい 基底 きてい 表示 ひょうじ 表示 ひょうじ 基底 きてい 全体 ぜんたい 空間 くうかん V を張 は 保証 ほしょう 一意 いちい 保証 ほしょう 基底 きてい R 3 基本 きほん x , y , z 高 こう 次元 じげん 場合 ばあい 同様 どうよう 対象 たいしょう 一般 いっぱん 化 か 見 み 空間 くうかん 観点 かんてん 座標 ざひょう 付 づ 述 の
基本 きほん
e 1 = (1, 0, ..., 0)e 2 = (0, 1, 0, ..., 0)e n は Fn の標準 ひょうじゅん 基底 きてい 呼 よ 基底 きてい 成 な 任意 にんい (x 1 , x 2 , ..., xn ) がこれらのベクトルの線型 せんけい 結合 けつごう 一意的 いちいてき
(
x
1
,
x
2
,
…
,
x
n
)
=
x
1
(
1
,
0
,
…
,
0
)
+
x
2
(
0
,
1
,
0
,
…
,
0
)
+
⋯
+
x
n
(
0
,
…
,
0
,
1
)
=
x
1
e
1
+
x
2
e
2
+
⋯
+
x
n
e
n
{\displaystyle {\begin{aligned}(x_{1},x_{2},\dotsc ,x_{n})&=x_{1}(1,0,\dotsc ,0)+x_{2}(0,1,0,\dotsc ,0)+\dotsb +x_{n}(0,\dotsc ,0,1)\\&=x_{1}{\boldsymbol {e}}_{1}+x_{2}{\boldsymbol {e}}_{2}+\dotsb +x_{n}{\boldsymbol {e}}_{n}\end{aligned}}}
と表 あらわ
任意 にんい 空間 くうかん 基底 きてい 持 も ツォルンの補題 ほだい から従 したが 従 したが ツェルメロ=フレンケル集合 しゅうごう 論 ろん の公理 こうり 与 あた 任意 にんい 空間 くうかん 基底 きてい 存在 そんざい 性 せい 選択 せんたく 公理 こうり 同値 どうち 選択 せんたく 公理 こうり 弱 よわ 超 ちょう 補題 ほだい (英語 えいご 版 ばん 与 あた 一 ひと 空間 くうかん V において任意 にんい 基底 きてい 同 おな 数 すう 元 もと 濃度 のうど 持 も 示 しめ ベクトル空間 くうかん 次元 じげん 定理 ていり (英語 えいご 版 ばん 濃度 のうど 空間 くうかん V の次元 じげん dim V と呼 よ 有限 ゆうげん 個 こ 張 は 空間 くうかん 場合 ばあい 上記 じょうき 主張 しゅちょう 集合 しゅうごう 論 ろん 的 てき 基礎 きそ 付 づ 抜 ぬ 示 しめ
数 かず 空間 くうかん Fn は、すでに示 しめ 基底 きてい 次元 じげん n であることがわかる。#函数 かんすう 空間 くうかん 節 ふし 述 の 多項式 たこうしき 環 たまき F [x ]次元 じげん 可算 かさん 集合 しゅうごう 基底 きてい 一 ひと 1, x , x 2 , … で与 あた 有界 ゆうかい 非 ひ 有界 ゆうかい 区間 くかん 上 じょう 函数 かんすう 全体 ぜんたい 成 な 空間 くうかん 一般 いっぱん 函数 かんすう 空間 くうかん 次元 じげん 当然 とうぜん 無限 むげん 大 だい [nb 4] 現 あらわ 係数 けいすう 対 たい 適当 てきとう 正則 せいそく 性 せい 条件 じょうけん 課 か 斉 ひとし 次 つぎ 常微分 じょうびぶん 方程式 ほうていしき 解 かい 空間 くうかん 次元 じげん 方程式 ほうていしき 階数 かいすう 等 ひと 例 たと 式 しき 1 解 かい 空間 くうかん e −x xe −x 生成 せいせい 二 ふた 函数 かんすう R 上 うえ 線型 せんけい 独立 どくりつ 空間 くうかん 次元 じげん 2 で、方程式 ほうていしき 階数 かいすう 2 と一致 いっち
有理数 ゆうりすう 体 たい Q 上 うえ 拡大 かくだい 体 たい Q (α あるふぁ 次元 じげん α あるふぁ 依存 いぞん 決 き α あるふぁ 有理数 ゆうりすう 係数 けいすう 代数 だいすう 方程式 ほうていしき
q
n
α あるふぁ
n
+
q
n
−
1
α あるふぁ
n
−
1
+
⋯
+
q
0
=
0
{\displaystyle q_{n}\alpha ^{n}+q_{n-1}\alpha ^{n-1}+\dotsb +q_{0}=0}
を満足 まんぞく α あるふぁ 代数 だいすう 的 てき 数 すう 次元 じげん 有限 ゆうげん 正確 せいかく 次元 じげん α あるふぁ 根 ね 持 も 最小 さいしょう 多項式 たこうしき 次数 じすう 等 ひと 例 たと 複素数 ふくそすう 体 たい C 実 じつ 二 に 次元 じげん 空間 くうかん 1 と虚数 きょすう 単位 たんい i で生成 せいせい 後者 こうしゃ 二 に 次 じ 方程式 ほうていしき i 2 + 1 = 0満足 まんぞく C 二 に 次元 じげん R 空間 くうかん 言 い 任意 にんい 体 からだ C 自身 じしん 上 うえ 空間 くうかん C 一 いち 次元 じげん 他方 たほう α あるふぁ 代数 だいすう 的 てき Q (α あるふぁ Q 上 うえ 次元 じげん 無限 むげん 大 だい 例 たと α あるふぁ π ぱい π ぱい 根 ね 代数 だいすう 方程式 ほうていしき 存在 そんざい 別 べつ 方 いかた π ぱい 超越 ちょうえつ 数 すう
線型 せんけい 写像 しゃぞう 行列 ぎょうれつ [ 編集 へんしゅう ] 二 ふた 空間 くうかん 間 あいだ 関係 かんけい 性 せい 線型 せんけい 写像 しゃぞう 線型 せんけい 変換 へんかん 表 あらわ 空間 くうかん 構造 こうぞう 反映 はんえい 写像 しゃぞう 即 すなわ 任意 にんい x y V 任意 にんい a ∈ F 対 たい
f
(
x
+
y
)
=
f
(
x
)
+
f
(
y
)
,
f
(
a
x
)
=
a
f
(
x
)
{\displaystyle f({\boldsymbol {x}}+{\boldsymbol {y}})=f({\boldsymbol {x}})+f({\boldsymbol {y}}),\quad f(a{\boldsymbol {x}})=af({\boldsymbol {x}})}
を満 み 意味 いみ 和 わ 積 せき 保 たも
同型 どうけい 写像 しゃぞう 線型 せんけい 写像 しゃぞう f : V → W 逆 ぎゃく 写像 しゃぞう g : W → V 即 すなわ 写像 しゃぞう 合成 ごうせい (f ◦ g ): W → W (g ◦ f ): V → V 恒等 こうとう 写像 しゃぞう 存在 そんざい 言 い 同 おな f は一対一 いちたいいち 単 たん 射 い 上 うえ 全 ぜん 射 い 線型 せんけい 写像 しゃぞう V と W の間 あいだ 同型 どうけい 写像 しゃぞう 存在 そんざい 互 たが 同型 どうけい V において成 な 立 た 任意 にんい 関係 かんけい 式 しき f を通 つう W における関係 かんけい 式 しき 写 うつ 逆 ぎゃく g を通 つう 行 おこな 意味 いみ 本質 ほんしつ 的 てき 同 おな 空間 くうかん 見 み
矢印 やじるし v 座標 ざひょう x と y で記述 きじゅつ 空間 くうかん 同型 どうけい 例 たと 平面 へいめん 上 じょう 有向 ゆうこう 線分 せんぶん 矢印 やじるし 成 な 空間 くうかん 数 かず 順序 じゅんじょ 対 たい 成 な 空間 くうかん 同型 どうけい 固定 こてい 座標 ざひょう 原点 げんてん 始点 してん 平面 へいめん 上 じょう 有向 ゆうこう 線分 せんぶん 図 ず 示 しめ 線分 せんぶん x -成分 せいぶん y -成分 せいぶん 考 かんが 順序 じゅんじょ 対 たい 表 あらわ 逆 ぎゃく 順序 じゅんじょ 対 たい (x , y ) が与 あた x だけ右 みぎ x が負 まけ |x | だけ左 ひだり 行 い y だけ上 うえ y が負 まけ |y | だけ下 した 行 い 有向 ゆうこう 線分 せんぶん v 得 え
固定 こてい 空間 くうかん 間 あいだ 線型 せんけい 写像 しゃぞう V → W 全体 ぜんたい 自体 じたい 線型 せんけい 空間 くうかん 成 な HomF V, W ) や L(V, W ) などで表 あらわ V から係数 けいすう 体 たい F への線型 せんけい 写像 しゃぞう 全体 ぜんたい 成 な 空間 くうかん V の双対 そうつい 空間 くうかん V ∗ 呼 よ 自然 しぜん 変換 へんかん V → V ∗∗ 通 つう 任意 にんい 空間 くうかん 二 に 重 じゅう 双対 そうつい 埋 う 込 こ 写像 しゃぞう 同型 どうけい 空間 くうかん 有限 ゆうげん 次元 じげん 時 とき 限 かぎ
V の基底 きてい 一 ひと 選 えら V の任意 にんい 元 もと 基底 きてい 線型 せんけい 結合 けつごう 一意的 いちいてき 表 あらわ 線型 せんけい 写像 しゃぞう f : V → W 基底 きてい 行 い 先 さき 決 き 完全 かんぜん 決定 けってい dim V = dim W V と W の基底 きてい 固定 こてい 間 あいだ 全 ぜん 単 たん 射 しゃ V の各 かく 基底 きてい 元 もと W の対応 たいおう 基底 きてい 元 もと 写 うつ 線型 せんけい 写像 しゃぞう 生 しょう 定義 ていぎ 同型 どうけい 写像 しゃぞう 従 したが 二 ふた 空間 くうかん 同型 どうけい 次元 じげん 一致 いっち 逆 ぎゃく 成 な 立 た 別 べつ 方 いかた 任意 にんい 空間 くうかん 次元 じげん 違 ちが 除 のぞ 完全 かんぜん 分類 ぶんるい 特 とく 任意 にんい n -次元 じげん F -ベクトル空間 くうかん V は Fn に同型 どうけい 標準 ひょうじゅん 的 てき 用意 ようい 同型 どうけい 存在 そんざい 実際 じっさい 同型 どうけい φ ふぁい Fn → V Fn の標準 ひょうじゅん 基底 きてい V に φ ふぁい 写 うつ V を選 えら 等価 とうか 適当 てきとう 基底 きてい 選 えら 自由 じゆう 度 ど 無限 むげん 次元 じげん 場合 ばあい 文脈 ぶんみゃく 特 とく 有効 ゆうこう 後述 こうじゅつ
典型 てんけい 的 てき 行列 ぎょうれつ 行列 ぎょうれつ 英 えい matrix 線型 せんけい 写像 しゃぞう 情報 じょうほう 記述 きじゅつ 有効 ゆうこう 概念 がいねん 行列 ぎょうれつ 図 ず 矩形 くけい 配列 はいれつ 書 か 任意 にんい m × n 行列 ぎょうれつ A は Fn から Fm への線型 せんけい 写像 しゃぞう
x
=
(
x
1
,
x
2
,
…
,
x
n
)
↦
(
∑
j
=
1
n
a
1
j
x
j
,
∑
j
=
1
n
a
2
j
x
j
,
…
,
∑
j
=
1
n
a
m
j
x
j
)
{\displaystyle {\boldsymbol {x}}=(x_{1},x_{2},\dotsc ,x_{n})\mapsto {\biggl (}\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\dotsc ,\sum _{j=1}^{n}a_{mj}x_{j}{\biggr )}}
として生 しょう ∑ は総和 そうわ 表 あらわ 行列 ぎょうれつ A と座標 ざひょう x 行列 ぎょうれつ 乗法 じょうほう 用 もち
x Ax と書 か 言 い V と W の基底 きてい 選 えら 任意 にんい 線型 せんけい 写像 しゃぞう f : V → W 同様 どうよう 方法 ほうほう 行列 ぎょうれつ 一意的 いちいてき 表 あらわ
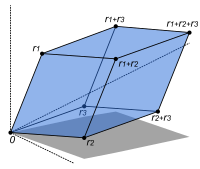
この平行 へいこう 六面体 ろくめんたい 体積 たいせき r 1 , r 2 , r 3 成 な 3 × 3 行列 ぎょうれつ 行列 ぎょうれつ 式 しき 絶対 ぜったい 値 ち 一致 いっち 正方 まさかた 行列 ぎょうれつ A の行列 ぎょうれつ 式 しき det (A ) は、A に対応 たいおう 線型 せんけい 写像 しゃぞう 同型 どうけい 否 ひ 測 はか 同型 どうけい 行列 ぎょうれつ 式 しき 値 ね 0 でないことが必要 ひつよう 十分 じゅうぶん n × n 実 じつ 行列 ぎょうれつ 対応 たいおう R n 線型 せんけい 変換 へんかん 向 む 保 たも 行列 ぎょうれつ 式 しき 正 せい 必要 ひつよう 十分 じゅうぶん
固有値 こゆうち 固有 こゆう [ 編集 へんしゅう ] 自己 じこ 準 じゅん 同型 どうけい 即 すなわ 線型 せんけい 写像 しゃぞう f : V → V 場合 ばあい v f による像 ぞう f (v 比較 ひかく 特 とく 重要 じゅうよう
任意 にんい 零 れい v λ らむだ 対 たい λ らむだ v f (v 満足 まんぞく f の固有値 こゆうち 英 えい eigenvalue λ らむだ 属 ぞく 固有 こゆう 英 えい eigenvector [nb 5] 同 おな 固有 こゆう v 差 さ f − λ らむだ 核 かく 元 もと Id は恒等 こうとう 写像 しゃぞう V → V V が有限 ゆうげん 次元 じげん 行列 ぎょうれつ 式 しき 使 つか 換 いか f が固有値 こゆうち λ らむだ 持 も
det
(
f
−
λ らむだ ⋅
Id
)
=
0
{\displaystyle \det(f-\lambda \cdot \operatorname {Id} )=0}
となることと同値 どうち 行列 ぎょうれつ 式 しき 定義 ていぎ 書 か 下 くだ 式 しき 左辺 さへん λ らむだ 変数 へんすう 多項式 たこうしき 見 み f の固有 こゆう 多項式 たこうしき 呼 よ 係数 けいすう 体 たい F がこの多項式 たこうしき 根 ね 含 ふく 程度 ていど 大 おお F = C F が代数 だいすう 的 てき 条件 じょうけん 自動的 じどうてき 満 み 任意 にんい 線型 せんけい 写像 しゃぞう 少 すく 一 ひと 固有 こゆう 持 も
ベクトル空間 くうかん V は固有 こゆう 基底 きてい (英語 えいご 版 ばん 固有 こゆう 基底 きてい 持 も 持 も 写像 しゃぞう ジョルダン標準 ひょうじゅん 形 がた によって制御 せいぎょ [nb 6] f の特定 とくてい 固有値 こゆうち λ らむだ 属 ぞく 固有 こゆう 全体 ぜんたい 成 な 集合 しゅうごう 固有値 こゆうち λ らむだ f )に対応 たいおう 固有 こゆう 空間 くうかん 呼 よ 空間 くうかん 成 な 無限 むげん 次元 じげん 場合 ばあい 対応 たいおう 主張 しゅちょう スペクトル定理 ていり に達 たっ 函数 かんすう 解析 かいせき 学 がく 道具立 どうぐだ 必要 ひつよう
基本 きほん 的 てき 構成 こうせい 法 ほう [ 編集 へんしゅう ] 上記 じょうき 具体 ぐたい 例 れい 加 くわ 与 あた 空間 くうかん 別 べつ 空間 くうかん 得 え 標準 ひょうじゅん 的 てき 線型 せんけい 代数 だいすう 学 がく 的 てき 構成 こうせい 存在 そんざい 以下 いか 述 の 定義 ていぎ 加 くわ 普遍 ふへん 性 せい 呼 よ 線型 せんけい 空間 くうかん X を X から他 た 任意 にんい 線型 せんけい 空間 くうかん 線型 せんけい 写像 しゃぞう 特定 とくてい 性質 せいしつ 特徴 とくちょう
部分 ぶぶん 空間 くうかん 商 しょう 空間 くうかん [ 編集 へんしゅう ] R 3 原点 げんてん 通 とお 直線 ちょくせん 青 あお 細 ほそ 線型 せんけい 部分 ぶぶん 空間 くうかん 二 ふた 平面 へいめん 緑 みどり 黄 き 交 まじ ベクトル空間 くうかん V の空 そら 部分 ぶぶん 集合 しゅうごう W が加法 かほう 乗法 じょうほう 下 した 閉 と 従 したが V の零 れい 含 ふく V の部分 ぶぶん 空間 くうかん V の部分 ぶぶん 空間 くうかん 自体 じたい 同 おな 体 たい 上 じょう 空間 くうかん 成 な 集合 しゅうごう S に対 たい 含 ふく 部分 ぶぶん 空間 くうかん 交 まじ S の線型 せんけい 包 つつみ 合 ごう S を含 ふく 最小 さいしょう V の部分 ぶぶん 空間 くうかん 成 な 属 ぞく 元 もと 言葉 ことば 言 い S の張 は 空間 くうかん S の元 もと 線型 せんけい 結合 けつごう 全体 ぜんたい 成 な 部分 ぶぶん 空間 くうかん
部分 ぶぶん 空間 くうかん 相対 そうたい 概念 がいねん 商 しょう 空間 くうかん 任意 にんい 部分 ぶぶん 空間 くうかん W ⊂ V 対 たい V を W で割 わ 商 しょう 空間 くうかん V /W 以下 いか 定義 ていぎ 集合 しゅうごう V /W v V の任意 にんい v W = {v w w W }形 かたち 集合 しゅうごう 全 すべ 二 ふた 元 もと v 1 + W v 2 + W 和 わ (v 1 + v 2 ) + W 倍 ばい 積 せき a (v W ) = (av ) + W 与 あた 定義 ていぎ 鍵 かぎ v 1 + W = v 2 + W 同値 どうち v 1 v 2 差 さ W に入 はい [nb 7] 方法 ほうほう 商 しょう 空間 くうかん 部分 ぶぶん 空間 くうかん W に含 ふく 情報 じょうほう 忘却 ぼうきゃく
線型 せんけい 写像 しゃぞう f : V → W 核 かく ker(f ) は W の零 れい 0 写 うつ v 核 かく 像 ぞう im(f ) = {f (v v V } はともにそれぞれ V および W の部分 ぶぶん 空間 くうかん 核 かく 像 ぞう 存在 そんざい 固定 こてい 体 からだ F )上 じょう 加 か 群 ぐん 圏 けん アーベル圏 けん (つまり、数学 すうがく 的 てき 対象 たいしょう 間 あいだ 構造 こうぞう 保 たも 写像 しゃぞう 集 あつ 即 すなわ 圏 けん アーベル群 ぐん 圏 けん と非常 ひじょう 似 に 振 ふ 舞 ま 成 な 要件 ようけん 一部 いちぶ 同型 どうけい 定理 ていり 線型 せんけい 代数 だいすう 学 がく 的 てき 方 いかた 階数 かいすう 退化 たいか 次数 じすう 定理 ていり
V
/
ker
(
f
)
≅
im
(
f
)
{\displaystyle V/{\ker(f)}\cong \operatorname {im} (f)}
や第 だい 二 に 第 だい 三 さん 同型 どうけい 定理 ていり 群論 ぐんろん 相当 そうとう 定理 ていり 同様 どうよう 仕方 しかた 定式 ていしき 化 か 証明 しょうめい
重要 じゅうよう 例 れい 適当 てきとう 固定 こてい 行列 ぎょうれつ A に対 たい 線型 せんけい 写像 しゃぞう x Ax 核 かく 写像 しゃぞう 核 かく Ax = 0満 み x 全体 ぜんたい 成 な 部分 ぶぶん 空間 くうかん A に属 ぞく 斉 ひとし 次 じ 線型 せんけい 方程式 ほうていしき 系 けい 解 かい 空間 くうかん 他 た 考 かんが 方 かた 線型 せんけい 微分 びぶん 方程式 ほうていしき
a
0
f
+
a
1
d
f
d
x
+
a
2
d
2
f
d
x
2
+
⋯
+
a
n
d
n
f
d
x
n
=
0
{\displaystyle a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0}
(各 かく 係数 けいすう ai も x の函数 かんすう 対 たい 拡張 かくちょう 対応 たいおう 線型 せんけい 写像 しゃぞう
f
↦
D
(
f
)
=
∑
i
=
0
n
a
i
d
i
f
d
x
i
{\displaystyle f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}}}
は函数 かんすう f の導 しるべ 函数 かんすう 例 たと f ′′(x )2 項 こう 現 あらわ 意味 いみ 線型 せんけい 現 あらわ 微分 びぶん 線型 せんけい 即 すなわ (f + g )′ = f ′ + g ′ 定数 ていすう c について
(cf )′ = cf ′ 成 な 立 た 上記 じょうき 作用素 さようそ 値 ね 線型 せんけい 線型 せんけい 微分 びぶん 作用素 さようそ 言 い 特 とく 微分 びぶん 方程式 ほうていしき D (f ) = 0解 かい 全体 ぜんたい R C 上 うえ 空間 くうかん
直積 ちょくせき 直和 なおかず [ 編集 へんしゅう ]
I
{\textstyle I}
添字 そえじ 付 つ 空間 くうかん 族 ぞく
V
i
{\textstyle V_{i}}
直積 ちょくせき
∏
i
∈
I
V
i
{\textstyle \prod _{i\in I}V_{i}}
順序 じゅんじょ 組 ぐみ
(
v
i
)
i
∈
I
=
(
v
1
,
v
2
,
…
)
(
v
i
∈
V
i
)
{\textstyle ({\boldsymbol {v}}_{i})_{i\in I}=({\boldsymbol {v}}_{1},{\boldsymbol {v}}_{2},\dotsc )\quad ({\boldsymbol {v}}_{i}\in V_{i})}
全体 ぜんたい 成 な 集合 しゅうごう 加法 かほう 乗法 じょうほう 成分 せいぶん 演算 えんざん 定 さだ 構成 こうせい 変種 へんしゅ 直和 なおかず
⨁
i
∈
I
V
i
{\textstyle \bigoplus _{i\in I}V_{i}}
余 よ 積 せき
∐
i
∈
I
V
i
{\textstyle \coprod _{i\in I}V_{i}}
先 さき 順序 じゅんじょ 組 ぐみ 有限 ゆうげん 個 こ 例外 れいがい 除 のぞ 全 すべ 成分 せいぶん 零 れい 許 ゆる 得 え 添字 そえじ 集合 しゅうごう
I
{\textstyle I}
有限 ゆうげん 二 ふた 構成 こうせい 一致 いっち 違 ちが 与 あた
同 おな 体 たい F 上 うえ 二 ふた 空間 くうかん V と W のテンソル積 せき (英 えい tensor product V ⊗F W 単 たん V ⊗ W 線型 せんけい 写像 しゃぞう 多 た 変数 へんすう 概念 がいねん 拡張 かくちょう 扱 あつか 多重 たじゅう 線型 せんけい 代数 だいすう 中心 ちゅうしん 的 てき 概念 がいねん 写像 しゃぞう g : V × W X ; (v w ↦ g (v w 双 そう 線型 せんけい 写像 しゃぞう g が両 りょう 変数 へんすう v w 何 いず 線型 せんけい 言 い w 固定 こてい 写像 しゃぞう v g (v w 線型 せんけい v 固定 こてい 時 とき 同様 どうよう 意味 いみ
テンソル積 せき 以下 いか 意味 いみ 双 そう 線型 せんけい 写像 しゃぞう 普遍 ふへん 的 てき 受 う 入 い 特別 とくべつ 空間 くうかん テンソル と呼 よ 記号 きごう 形式 けいしき 的 てき 有限 ゆうげん 和 わ
v
1
⊗
w
1
+
v
2
⊗
w
2
+
⋯
+
v
n
⊗
w
n
{\displaystyle {\boldsymbol {v}}_{1}\otimes {\boldsymbol {w}}_{1}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}_{2}+\dotsb +{\boldsymbol {v}}_{n}\otimes {\boldsymbol {w}}_{n}}
の全体 ぜんたい 線型 せんけい 空間 くうかん 元 もと a をスカラーとして
a
(
v
⊗
w
)
=
(
a
v
)
⊗
w
=
v
⊗
(
a
w
)
{\displaystyle a({\boldsymbol {v}}\otimes {\boldsymbol {w}})=(a{\boldsymbol {v}})\otimes {\boldsymbol {w}}={\boldsymbol {v}}\otimes (a{\boldsymbol {w}})}
v
1
+
v
2
⊗
w
=
v
1
⊗
w
+
v
2
⊗
w
{\displaystyle {\boldsymbol {v}}_{1}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}={\boldsymbol {v}}_{1}\otimes {\boldsymbol {w}}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}}
v
⊗
(
w
1
+
w
2
)
=
v
⊗
w
1
+
v
⊗
w
2
{\displaystyle {\boldsymbol {v}}\otimes ({\boldsymbol {w}}_{1}+{\boldsymbol {w}}_{2})={\boldsymbol {v}}\otimes {\boldsymbol {w}}_{1}+{\boldsymbol {v}}\otimes {\boldsymbol {w}}_{2}}
なる規則 きそく 縛 しば
テンソル積 せき 普遍 ふへん 性 せい 表 あらわ 可 か 換 かわ 図式 ずしき これらの規則 きそく 写像 しゃぞう f : V × W → V ⊗ W ; (v w v w 双 そう 線型 せんけい 保証 ほしょう 積 せき 普遍 ふへん 性 せい
任意 にんい 空間 くうかん X と任意 にんい 双 そう 線型 せんけい 写像 しゃぞう g : V × W → X 与 あた 写像 しゃぞう u : V ⊗ W → X 一意的 いちいてき 存在 そんざい 上記 じょうき 写像 しゃぞう f との合成 ごうせい u ◦ f g に等 ひと u (v w g (v w [48] というものである。テンソル積 せき 普遍 ふへん 性 せい 対象 たいしょう 対象 たいしょう 対象 たいしょう 写像 しゃぞう 間接 かんせつ 的 てき 定義 ていぎ 進 すす 抽象 ちゅうしょう 代数 だいすう 学 がく 用 もち 手法 しゅほう 一 いち 例 れい
付加 ふか 構造 こうぞう 備 そな 空間 くうかん [ 編集 へんしゅう ] 線型 せんけい 代数 だいすう 学 がく 観点 かんてん 任意 にんい 空間 くうかん 同型 どうけい 除 のぞ 次元 じげん 特徴 とくちょう 意味 いみ 空間 くうかん 完全 かんぜん 分 わ 空間 くうかん 本質 ほんしつ 的 てき 函 はこ 数列 すうれつ 別 べつ 函数 かんすう 収束 しゅうそく 否 ひ 解析 かいせき 学 がく 重要 じゅうよう 問題 もんだい 取 と 扱 あつか 枠組 わくぐ 提供 ていきょう 同様 どうよう 加法 かほう 演算 えんざん 有限 ゆうげん 項 こう 和 わ 許 ゆる 線型 せんけい 代数 だいすう 学 がく 無限 むげん 級数 きゅうすう 扱 あつか 適当 てきとう 従 したが 函数 かんすう 解析 かいせき 学 がく 空間 くうかん 更 さら 構造 こうぞう 考 かんが 必要 ひつよう 求 もと 同様 どうよう 付加 ふか 的 てき 情報 じょうほう 持 も 空間 くうかん 有効 ゆうこう 働 はたら 部分 ぶぶん 抽象 ちゅうしょう 的 てき 見 み 公理 こうり 的 てき 取扱 とりあつか 空間 くうかん 持 も 代数 だいすう 学 がく 的 てき 本質 ほんしつ 的 てき 特徴 とくちょう 浮 う 彫 ぼ [要 よう 出典 しゅってん 。
付加 ふか 構造 こうぞう 一 ひと 例 れい 順序 じゅんじょ 集合 しゅうごう ≤ で、これによりベクトルの比較 ひかく 行 おこな 例 たと 実 みのる n -次元 じげん 空間 くうかん R n 成分 せいぶん 比較 ひかく 順序 じゅんじょ ルベーグ積分 せきぶん は函数 かんすう 二 ふた 正 せい 値 ね 函数 かんすう 差 さ
f
=
f
+
−
f
−
{\displaystyle f=f^{+}-f^{-}}
として(f + f の正 せい 部分 ぶぶん f − 負 ふ 部分 ぶぶん 表 あらわ 依拠 いきょ 順序 じゅんじょ 線型 せんけい 空間 くうかん (英語 えいご 版 ばん 例 たと リース空間 くうかん )はルベーグ積分 せきぶん において基本 きほん 的 てき
ノルム空間 くうかん 内積 ないせき 空間 くうかん [ 編集 へんしゅう ] ベクトルの「測度 そくど 長 なが 測 はか ノルム や、ベクトルの間 あいだ 角 かく 測 はか 内積 ないせき 決 き 与 あた 定義 ていぎ 空間 くうかん 空間 くうかん |v のように表 あらわ 内積 ないせき 定義 ていぎ 空間 くうかん 内積 ないせき 空間 くうかん 呼 よ 内積 ないせき ⟨v w のように表 あらわ 内積 ないせき 空間 くうかん 付随 ふずい
|
v
|
:=
⟨
v
,
v
⟩
{\displaystyle |{\boldsymbol {v}}|:={\sqrt {\langle {\boldsymbol {v}},{\boldsymbol {v}}\rangle }}}
を持 も
数 かず 空間 くうかん Fn は標準 ひょうじゅん 内積 ないせき
x
⋅
y
=
x
1
y
1
+
⋯
+
x
n
y
n
{\displaystyle {\boldsymbol {x}}\cdot {\boldsymbol {y}}=x_{1}y_{1}+\dotsb +x_{n}y_{n}}
を備 そな R 2 二 ふた x y 成 な 角 かく θ しーた 概念 がいねん 余弦 よげん 定理 ていり
x
⋅
y
=
|
x
|
|
y
|
cos
(
θ しーた )
{\displaystyle {\boldsymbol {x}}\cdot {\boldsymbol {y}}={\mathopen {|}}{\boldsymbol {x}}{\mathclose {|}}{\mathopen {|}}{\boldsymbol {y}}{\mathclose {|}}\cos(\theta )}
によって反映 はんえい x y 満 み 二 ふた x y 互 たが 直交 ちょっこう 言 い 標準 ひょうじゅん 内積 ないせき 重要 じゅうよう 変形 へんけい 版 ばん ミンコフスキー空間 くうかん R 4 = R 3,1 積 つもる
⟨
x
∣
y
⟩
=
x
1
y
1
+
x
2
y
2
+
x
3
y
3
−
x
4
y
4
{\displaystyle \langle {\boldsymbol {x}}\mid {\boldsymbol {y}}\rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}}
を備 そな 標準 ひょうじゅん 内積 ないせき 大 おお 違 ちが 積 つもる 正 せい 定値 ていち ⟨x x は負 まけ 値 ね 取 と 得 え 例 たと x 三 みっ 空間 くうかん 的 てき 座標 ざひょう 異 こと 時間 じかん 対応 たいおう 第 だい 四 よん 座標 ざひょう 考 かんが 特殊 とくしゅ 相対性理論 そうたいせいりろん 数学 すうがく 的 てき 取扱 とりあつか 有効 ゆうこう
線型 せんけい 位相 いそう 空間 くうかん [ 編集 へんしゅう ] 収束 しゅうそく 性 せい 問題 もんだい 空間 くうかん V に両立 りょうりつ 位相 いそう 近 ちか 記述 きじゅつ 可能 かのう 構造 こうぞう 入 い 扱 あつか 両立 りょうりつ 加法 かほう 乗法 じょうほう 連続 れんぞく 写像 しゃぞう 意味 いみ 大雑把 おおざっぱ 言 い x y V a ∈ F 限 かぎ 範囲 はんい 中 なか x y ax 限 かぎ 範囲 はんい 留 と [nb 8] 議論 ぎろん 意味 いみ 持 も 文脈 ぶんみゃく 体 からだ F にも位相 いそう 定 さだ 用 もち 実数 じっすう 体 たい 複素数 ふくそすう 体 たい
このような線型 せんけい 位相 いそう 空間 くうかん 項 こう 級数 きゅうすう 考 かんが V の元 もと 列 れつ (fi )i ∈ N の無限 むげん 和 わ
∑
i
=
0
∞
f
i
{\displaystyle \sum _{i=0}^{\infty }f_{i}}
とは、対応 たいおう 有限 ゆうげん 部分 ぶぶん 和 わ 極限 きょくげん 表 あらわ 例 たと fi が、ある(実 じつ 複素 ふくそ 函数 かんすう 空間 くうかん 属 ぞく 函数 かんすう 場合 ばあい 級数 きゅうすう 函数 かんすう 項 こう 級数 きゅうすう 呼 よ 函数 かんすう 項 こう 級数 きゅうすう 収束 しゅうそく 様態 ようたい (英語 えいご 版 ばん 函数 かんすう 空間 くうかん 課 か 位相 いそう 依存 いぞん 様態 ようたい 中 なか 各 かく 点 てん 収束 しゅうそく 一様 いちよう 収束 しゅうそく 二 ふた 特 とく 際立 きわだ 例 れい
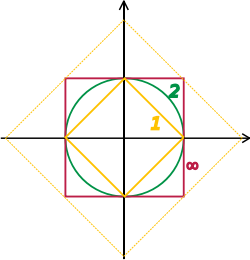
R 2 単位 たんい 球面 きゅうめん 1 の平面 へいめん 図 ず 異 こと p -ノルム関 かん 単位 たんい 球面 きゅうめん p = 1, 2, ∞場合 ばあい 描 えが 大 おお 菱形 ひしがた 1 -ノルムが √ 2 等 ひと 点 てん 描 えが ある種 しゅ 無限 むげん 級数 きゅうすう 極限 きょくげん 存在 そんざい 保証 ほしょう 方法 ほうほう 一 ひと 考 かんが 空間 くうかん 任意 にんい コーシー列 れつ が収束 しゅうそく 限 かぎ 考 かんが 空間 くうかん 完備 かんび 距離 きょり 空間 くうかん 大 おお 言 い 空間 くうかん 完備 かんび 必要 ひつよう 極限 きょくげん 含 ふく 例 たと 単位 たんい 区間 くかん [0, 1] 上 うえ 多項式 たこうしき 函数 かんすう 全体 ぜんたい 成 な 空間 くうかん 一様 いちよう 収束 しゅうそく 位相 いそう 入 い 完備 かんび [0, 1] 上 うえ 任意 にんい 連続 れんぞく 函数 かんすう 多項式 たこうしき 函 はこ 数列 すうれつ 一様 いちよう 近似 きんじ ストーン=ワイエルシュトラスの定理 ていり による。対照 たいしょう 的 てき 区間 くかん [0, 1] 上 うえ 連続 れんぞく 函数 かんすう 全体 ぜんたい 成 な 空間 くうかん 同 おな 位相 いそう 入 い 完備 かんび 列 れつ v n v 収束 しゅうそく 必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん
lim
n
→
∞
|
v
n
−
v
|
=
0
{\displaystyle \lim _{n\to \infty }|{\boldsymbol {v}}_{n}-{\boldsymbol {v}}|=0}
で定 さだ 空間 くうかん 位相 いそう 入 はい 空間 くうかん 空間 くうかん 内積 ないせき 定 さだ 位相 いそう 関 かん 完備 かんび 位相 いそう 空間 くうかん 函数 かんすう 解析 かいせき 学 がく 重要 じゅうよう 研究 けんきゅう 有限 ゆうげん 次元 じげん 位相 いそう 線型 せんけい 空間 くうかん 上 じょう 同 おな 収束 しゅうそく 性 せい 概念 がいねん 定 さだ 無限 むげん 次元 じげん 空間 くうかん 焦点 しょうてん 図 ず R 2 上 うえ 1 ノルムと ∞ ノルムとの同値 どうち 性 せい 示 しめ 単位 たんい 球体 きゅうたい 互 たが 他 た 囲 かこ 列 れつ 1 ノルムに関 かん 0 に収束 しゅうそく 列 れつ ∞ ノルムに関 かん 収束 しゅうそく 同値 どうち 無限 むげん 次元 じげん 空間 くうかん 場合 ばあい 一般 いっぱん 互 たが 同値 どうち 位相 いそう 存在 そんざい 位相 いそう 線型 せんけい 空間 くうかん 研究 けんきゅう 付加 ふか 構造 こうぞう 持 も 純 じゅん 代数 だいすう 的 てき 空間 くうかん 理論 りろん 豊 ゆた
概念的 がいねんてき 観点 かんてん 位相 いそう 線型 せんけい 空間 くうかん 関 かん 全 すべ 概念 がいねん 位相 いそう 合 あ 例 たと 位相 いそう 線型 せんけい 空間 くうかん 間 あいだ 線型 せんけい 写像 しゃぞう 線型 せんけい 汎 ひろし 函数 かんすう V → W 連続 れんぞく 仮定 かてい 特 とく 位相 いそう 的 てき 双対 そうつい 空間 くうかん V ∗ 連続 れんぞく 汎 ひろし 函数 かんすう V → R (or C )基礎 きそ 成 な ハーン-バナッハの定理 ていり は、適当 てきとう 位相 いそう 線型 せんけい 空間 くうかん 連続 れんぞく 汎 ひろし 函数 かんすう 部分 ぶぶん 空間 くうかん 分 わ 関係 かんけい
ステファン・バナフ の導入 どうにゅう バナッハ空間 くうかん とは、完備 かんび 空間 くうかん 一 ひと 例 れい
ℓ
p
{\displaystyle \ell ^{p}}
(1 ≤ p ≤ ∞) は、実数 じっすう 成分 せいぶん 無限 むげん 次元 じげん x x 1 , x 2 , ...)p < ∞対 たい
|
x
|
p
:=
(
∑
i
|
x
i
|
p
)
1
/
p
{\displaystyle |{\boldsymbol {x}}|_{p}:={\biggl (}\sum _{i}|x_{i}|^{p}{\biggr )}^{1/p}}
または p = ∞対 たい
|
x
|
∞
:=
sup
i
|
x
i
|
{\displaystyle |{\boldsymbol {x}}|_{\infty }:=\sup _{i}|x_{i}|}
で定義 ていぎ p -ノルムが有限 ゆうげん 全体 ぜんたい 成 な 空間 くうかん 無限 むげん 次元 じげん 空間 くうかん
ℓ
p
{\displaystyle \ell ^{p}}
位相 いそう 異 こと p に対 たい 同値 どうち 例 たと 列 れつ x n −n , 2−n , ..., 2−n , 0, 0, ...)各項 かくこう 最初 さいしょ 2n -個 こ 成分 せいぶん 2−n で残 のこ 0 となるような無限 むげん 次元 じげん 列 れつ p = ∞零 れい 収束 しゅうそく p = 1式 しき
|
x
n
|
∞
=
sup
(
2
−
n
,
0
)
=
2
−
n
→
0
{\displaystyle |x_{n}|_{\infty }=\sup(2^{-n},0)=2^{-n}\to 0}
だが
|
x
n
|
1
=
∑
i
=
1
2
n
2
−
n
=
2
n
⋅
2
−
n
=
1
{\displaystyle |x_{n}|_{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1}
である。
実 じつ 数列 すうれつ 一般 いっぱん 函数 かんすう f : Ω おめが R 上記 じょうき 和 わ ルベーグ積分 せきぶん に置 お 換 か
|
f
|
p
:=
(
∫
Ω おめが
|
f
(
x
)
|
p
d
x
)
1
/
p
{\displaystyle |f|_{p}:=\left(\int _{\Omega }{\bigl |}f(x){\bigr |}^{p}\,dx\right)^{1/p}}
をノルムとして備 そな 与 あた 領域 りょういき Ω おめが 例 たと 区間 くかん 上 じょう |f |p を満足 まんぞく 可 か 積分 せきぶん 函数 かんすう 空間 くうかん 入 い ルベーグ空間 くうかん Lp (Ω おめが 呼 よ [nb 9] 空間 くうかん 何 いず 完備 かんび 上記 じょうき 積分 せきぶん リーマン積分 せきぶん としたならば、空間 くうかん 完備 かんび 積分 せきぶん 論 ろん 考 かんが 正当 せいとう 性 せい 一 ひと 挙 あ 理由 りゆう 一 ひと [nb 10] 具体 ぐたい 的 てき 書 か 任意 にんい 可 か 積分 せきぶん 函 はこ 数列 すうれつ f 1 , f 2 , ...|f n p 条件 じょうけん
lim
k
,
n
→
∞
∫
Ω おめが
|
f
k
(
x
)
−
f
n
(
x
)
|
p
d
x
=
0
{\displaystyle \lim _{k,\ n\to \infty }\int _{\Omega }{\bigl |}f_{k}(x)-f_{n}(x){\bigr |}^{p}\,dx=0}
を満足 まんぞく 適当 てきとう 函数 かんすう f (x )空間 くうかん Lp (Ω おめが 属 ぞく 存在 そんざい
lim
k
→
∞
∫
Ω おめが
|
f
(
x
)
−
f
k
(
x
)
|
p
d
x
=
0
{\displaystyle \lim _{k\to \infty }\int _{\Omega }{\bigl |}f(x)-f_{k}(x){\bigr |}^{p}\,dx=0}
を満 み
函数 かんすう 自体 じたい 導 しるべ 函数 かんすう 有界 ゆうかい 性 せい 条件 じょうけん 課 か ソボレフ空間 くうかん の概念 がいねん 導 みちび
正弦 せいげん 函数 かんすう 赤 あか 有限 ゆうげん 和 わ 周期 しゅうき 函数 かんすう 青 あお 近似 きんじ 様子 ようす 初 はつ 項 こう 項 こう 和 わ 順 じゅん 示 しめ 示 しめ 完備 かんび 内積 ないせき 空間 くうかん ダフィット・ヒルベルト に因 ちな ヒルベルト空間 くうかん (英 えい Hilbert space 呼 よ 自乗 じじょう 可 か 積分 せきぶん 函数 かんすう 空間 くうかん L 2 (Ω おめが
⟨
f
,
g
⟩
=
∫
Ω おめが
f
(
x
)
g
(
x
)
¯
d
x
{\displaystyle \langle f,g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx}
で定義 ていぎ 内積 ないせき g (x )g (x )複素 ふくそ 共役 きょうやく [nb 11] 入 い 主要 しゅよう 空間 くうかん 例 れい
定義 ていぎ 空間 くうかん 任意 にんい 列 れつ 極限 きょくげん 持 も 逆 ぎゃく 与 あた 極限 きょくげん 函数 かんすう 近似 きんじ 適当 てきとう 性質 せいしつ 持 も 函 はこ 数列 すうれつ fn を求 もと 重要 じゅうよう 初期 しょき 解析 かいせき 学 がく 近似 きんじ 形 かたち 可 か 微分 びぶん 函数 かんすう f の多項式 たこうしき 列 れつ 近似 きんじ 確立 かくりつ ストーン=ヴァイアシュトラスの定理 ていり により、[a , b ] 上 うえ 任意 にんい 連続 れんぞく 函数 かんすう 適当 てきとう 多項式 たこうしき 列 れつ 近 ちか 近似 きんじ 三角 さんかく 関数 かんすう 用 もち 同様 どうよう 近似 きんじ 法 ほう 一般 いっぱん 展開 てんかい 呼 よ 工学 こうがく 広 ひろ 応用 おうよう #フーリエ変換 へんかん 節 ふし 参照 さんしょう 一般 いっぱん 概念的 がいねんてき 言 い 定理 ていり 基本 きほん 函数 かんすう 族 ぞく 何 なに 端的 たんてき 記述 きじゅつ 抽象 ちゅうしょう 空間 くうかん 基本 きほん 族 ぞく 空間 くうかん H を位相 いそう 的 てき 生成 せいせい 十分 じゅうぶん 位相 いそう 的 てき 生成 せいせい 単 たん 生成 せいせい 位相 いそう 的 てき 線型 せんけい 包 つつみ 呼 よ 線型 せんけい 包 つつみ 閉包 へいほう 即 すなわ 有限 ゆうげん 線型 せんけい 結合 けつごう 極限 きょくげん 全体 ぜんたい 空間 くうかん 一致 いっち 函数 かんすう 集合 しゅうごう H の基底 きてい 基底 きてい 呼 よ 基底 きてい 濃度 のうど 空間 くうかん H のヒルベルト次元 じげん と呼 よ [nb 12] 定理 ていり 適当 てきとう 基底 きてい 函数 かんすう 族 ぞく 近似 きんじ 目的 もくてき 十分 じゅうぶん 性 せい 示 しめ グラム・シュミットの正規 せいき 直交 ちょっこう 化 か 法 ほう を用 もち 正規 せいき 直交 ちょっこう 基底 きてい 得 え 意味 いみ 直交 ちょっこう 基底 きてい 有限 ゆうげん 次元 じげん ユークリッド空間 くうかん における座標軸 ざひょうじく 空間 くうかん 対 たい 一般 いっぱん 化 か 考 かんが
様々 さまざま 微分 びぶん 方程式 ほうていしき 対 たい 解 かい 空間 くうかん 言葉 ことば 解釈 かいしゃく 例 たと 物理 ぶつり 学 がく 工学 こうがく 多 おお 分野 ぶんや 方程式 ほうていしき 導 みちび 特定 とくてい 物理 ぶつり 的 てき 性質 せいしつ 持 も 解 かい 直交 ちょっこう 基底 きてい 函数 かんすう 族 ぞく 扱 あつか 物理 ぶつり 学 がく 例 れい 量子力学 りょうしりきがく 時間 じかん 依存 いぞん シュレーディンガー方程式 ほうていしき は、その解 かい 波動 はどう 関数 かんすう 呼 よ 偏 へん 微分 びぶん 方程式 ほうていしき 物理 ぶつり 的 てき 性質 せいしつ 時間 じかん 的 てき 変化 へんか 記述 きじゅつ 物理 ぶつり 的 てき 性質 せいしつ 対 たい 明確 めいかく 値 ね 種 しゅ 線型 せんけい 微分 びぶん 作用素 さようそ 固有値 こゆうち 属 ぞく 固有 こゆう 状態 じょうたい 呼 よ 波動 はどう 函数 かんすう 対応 たいおう スペクトル定理 ていり は、函数 かんすう 作用 さよう 線型 せんけい コンパクト作用素 さようそ を、それらの固有値 こゆうち 固有 こゆう 函数 かんすう 用 もち 分解 ぶんかい 述 の
体 からだ 上 じょう 多元 たげん 環 たまき [ 編集 へんしゅう ] 方程式 ほうていしき xy = 1与 あた 双曲線 そうきょくせん 双曲線 そうきょくせん 上 じょう 函数 かんすう 座標 ざひょう 環 たまき R [x , y ] / (xy − 1)与 あた R 上 うえ 無限 むげん 次元 じげん 空間 くうかん 一般 いっぱん 空間 くうかん 間 あいだ 乗法 じょうほう 持 も 二 ふた 乗法 じょうほう 定 さだ 双 そう 線型 せんけい 写像 しゃぞう 付加 ふか 的 てき 備 そな 空間 くうかん 体 からだ 上 じょう 多元 たげん 環 たまき 言 い 主 おも 多元 たげん 環 たまき 何 なん 幾何 きか 学 がく 的 てき 対象 たいしょう 上 うえ 函数 かんすう 空間 くうかん 生 しょう 体 からだ 値 ね 函数 かんすう 点 てん 乗法 じょうほう 持 も 函数 かんすう 全体 ぜんたい 多元 たげん 環 たまき 成 な 例 たと 定理 ていり 空間 くうかん 多元 たげん 環 たまき バナッハ環 たまき において成立 せいりつ
可 か 換 かわ 多元 たげん 環 たまき 一 いち 変数 へんすう 多 た 変数 へんすう 多項式 たこうしき 環 たまき 使 つか 作 つく 可 か 換 かわ 多元 たげん 環 たまき 乗法 じょうほう 可 か 換 かわ 結合 けつごう 的 てき 環 たまき 剰余 じょうよ 環 たまき 代数 だいすう 幾何 きか 的 てき 対象 たいしょう 上 じょう 函数 かんすう 環 たまき 代数 だいすう 幾何 きか 学 がく 基礎 きそ 成 な
別 べつ 重要 じゅうよう 例 れい 環 たまき 環 たまき 乗法 じょうほう x , y 積 せき [x , y ] と書 か 可 か 換 かわ 結合 けつごう 的 てき 制約 せいやく 条件 じょうけん
反対称 はんたいしょう 性 せい [x , y ] = −[y , x ] ヤコビの等式 とうしき : [x , [y , z ]] + [y , [z , x ]] + [z , [x , y ]] = 0 によって制限 せいげん 環 たまき 例 れい n -次 じ 正方 せいほう 行列 ぎょうれつ 全体 ぜんたい 成 な 空間 くうかん 行列 ぎょうれつ 交換 こうかん 子 こ [x , y ] = xy − yx 積 せき R 3 クロス積 せき を入 い 含 ふく
テンソル代数 だいすう T(V ) は任意 にんい 空間 くうかん 積 せき 導入 どうにゅう 多元 たげん 環 たまき 得 え 形式 けいしき 的 てき 方法 ほうほう T(V ) はベクトル空間 くうかん 単純 たんじゅん テンソル あるいは分解 ぶんかい 可能 かのう 型 がた 呼 よ 記号 きごう
v
1
⊗
v
2
⊗
⋯
⊗
v
n
{\displaystyle {\boldsymbol {v}}_{1}\otimes {\boldsymbol {v}}_{2}\otimes \dotsb \otimes {\boldsymbol {v}}_{n}}
によって生成 せいせい テンソルの階数 かいすう (英語 えいご 版 ばん n は任意 にんい 動 うご 乗法 じょうほう 二 ふた 空間 くうかん 対 たい テンソル積 せき を定義 ていぎ 同 おな 基底 きてい 元 もと 記号 きごう 積 せき ⊗ で結合 けつごう 与 あた 一般 いっぱん 加法 かほう 対 たい 分配 ぶんぱい 法則 ほうそく 基底 きてい 元 もと 対 たい 積 せき 延長 えんちょう 倍 ばい 積 せき ⊗ と可 か 換 かわ 得 え T(V ) においては、一般 いっぱん v 1 ⊗ v 2 v 2 ⊗ v 1 間 あいだ 何 なん 関係 かんけい 成立 せいりつ 二 ふた 元 もと 強制 きょうせい 的 てき 等 ひと 定 さだ 対称 たいしょう 代数 だいすう S(V ) が、あるいは強制 きょうせい 的 てき v 1 ⊗ v 2 = − v 2 ⊗ v 1 置 お 外積 がいせき 代数 だいすう
⋀
(
V
)
{\textstyle \bigwedge (V)}
得 え
基礎 きそ 体 からだ F を明示 めいじ 場合 ばあい F -多元 たげん 環 たまき F -代数 だいすう 言葉 ことば 用 もち
ベクトル空間 くうかん 多様 たよう 体 たい 対 たい 応用 おうよう 様々 さまざま 状況 じょうきょう 生 しょう 多様 たよう 体 たい 上 じょう 定義 ていぎ 体 からだ 値 ね 函数 かんすう 考 かんが 空間 くうかん 生 しょう 空間 くうかん 考 かんが 解析 かいせき 学 がく 幾何 きか 学 がく 問題 もんだい 取 と 扱 あつか 枠組 わくぐ 提供 ていきょう 空間 くうかん 変換 へんかん 利用 りよう 挙 あ 例 れい 網羅 もうら 的 てき 例 たと 数理 すうり 最適 さいてき 化 か 多 おお 応用 おうよう 存在 そんざい ゲーム理論 りろん のミニマックス法 ほう は全 すべ 最適 さいてき 試行 しこう 行 おこな 一意的 いちいてき 得 え 述 の 空間 くうかん 法 ほう 用 もち 証明 しょうめい 表現 ひょうげん 論 ろん 分 わ 線型 せんけい 代数 だいすう 学 がく 空間 くうかん 関 かん 内容 ないよう 群論 ぐんろん 他 た 領域 りょういき 実 みの 豊 ゆた 引 ひ 写 うつ [77]
シュワァルツ超 ちょう 函数 かんすう [ 編集 へんしゅう ] シュヴァルツ超 ちょう 函数 かんすう (英 えい distribution 各 かく 試験 しけん 函数 かんすう 典型 てんけい 的 てき 関数 かんすう 台 だい 持 も 滑 なめ 関数 かんすう 数 かず 連続 れんぞく 的 てき 仕方 しかた 割 わ 当 あ 線型 せんけい 写像 しゃぞう 即 すなわ 超 ちょう 函数 かんすう 空間 くうかん 試験 しけん 函数 かんすう 空間 くうかん 連続 れんぞく 的 てき 双対 そうつい 後者 こうしゃ 空間 くうかん 試験 しけん 函数 かんすう f それ自体 じたい 高階 たかしな 導 しるべ 函数 かんすう 考慮 こうりょ 位相 いそう 入 はい 超 ちょう 函数 かんすう 典型 てんけい 的 てき 例 れい 領域 りょういき Ω おめが 上 うえ 試験 しけん 函数 かんすう f を積分 せきぶん 作用素 さようそ
I
(
f
)
=
∫
Ω おめが
f
(
x
)
d
x
{\displaystyle I(f)=\int _{\Omega }f(x)\,dx}
である。Ω おめが 一 いち 点 てん 集合 しゅうごう {p } のとき、これは試験 しけん 函数 かんすう f に点 てん p における値 ね 割 わ 当 あ ディラックのデルタ関数 かんすう δ でるた 定 さだ δ でるた f ) = f (p )
シュヴァルツ超 ちょう 函数 かんすう 微分 びぶん 方程式 ほうていしき 解 と 強力 きょうりょく 道具 どうぐ 微分 びぶん 線型 せんけい 解析 かいせき 学 がく 標準 ひょうじゅん 的 てき 概念 がいねん 自然 しぜん 超 ちょう 函数 かんすう 空間 くうかん 延長 えんちょう 従 したが 問題 もんだい 方程式 ほうていしき 超 ちょう 函数 かんすう 空間 くうかん 引 ひ 写 うつ 超 ちょう 函数 かんすう 空間 くうかん 函数 かんすう 空間 くうかん 大 おお 方程式 ほうていしき 解 と 柔軟 じゅうなん 方法 ほうほう 利用 りよう 例 たと グリーン関数 かんすう 法 ほう
また、基本 きほん 解 かい 真 しん 函数 かんすう 超 ちょう 函数 かんすう 解 かい 弱 じゃく 解 かい 弱 じゃく 解 かい 所期 しょき 境界 きょうかい 条件 じょうけん 満 み 方程式 ほうていしき 真 しん 解 かい 求 もと 見 み 弱 じゃく 解 かい 実際 じっさい 真 しん 函数 かんすう 確 たし 証明 しょうめい 場合 ばあい 方程式 ほうていしき 真 しん 解 かい 例 たと リースの表現 ひょうげん 定理 ていり の帰結 きけつ 弱 じゃく 形式 けいしき 利用 りよう
熱 ねつ 方程式 ほうていしき 冷 つめ 環境 かんきょう 熱源 ねつげん 温度 おんど 低下 ていか 時間 じかん 散逸 さんいつ 物理 ぶつり 的 てき 性質 せいしつ 記述 きじゅつ 黄色 おうしょく 赤 あか 冷 つめ 領域 りょういき 表 あらわ 周期 しゅうき 関数 かんすう フーリエ級数 きゅうすう 成 な 三角 さんかく 関数 かんすう 和 わ 分解 ぶんかい 物理 ぶつり 学 がく 工学 こうがく 用 もち 手法 しゅほう [nb 13] [80] 台 だい 空間 くうかん ヒルベルト空間 くうかん L 2 (0, 2π ぱい 函数 かんすう 族 ぞく sin mx および cos mx (m は整数 せいすう 正規 せいき 直交 ちょっこう 基底 きてい 与 あた L 2 函数 かんすう f のフーリエ展開 てんかい
a
0
2
+
∑
m
=
1
∞
[
a
m
cos
(
m
x
)
+
b
m
sin
(
m
x
)
]
{\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }{\bigl [}a_{m}\cos(mx)+b_{m}\sin(mx){\bigr ]}}
である。係数 けいすう am , bm は f のフーリエ係数 けいすう 呼 よ 公式 こうしき
a
m
=
1
π ぱい
∫
0
2
π ぱい
f
(
t
)
cos
(
m
t
)
d
t
,
b
m
=
1
π ぱい
∫
0
2
π ぱい
f
(
t
)
sin
(
m
t
)
d
t
{\displaystyle a_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\cos(mt)dt,\quad b_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(mt)dt}
で求 もと
物理 ぶつり 学 がく 言葉 ことば 言 い 函数 かんすう 正弦 せいげん 波 は 重 かさ 合 あわ 表 あらわ 係数 けいすう 函数 かんすう 周波数 しゅうはすう 情報 じょうほう 与 あた 複素 ふくそ 型 がた 級数 きゅうすう 広 ひろ 用 もち 上記 じょうき 具体 ぐたい 的 てき 公式 こうしき 一般 いっぱん ポントリャーギン双対 そうつい と呼 よ 双対 そうつい 帰結 きけつ 加法 かほう 群 ぐん R 双対 そうつい 性 せい 適用 てきよう 古典 こてん 的 てき 変換 へんかん 得 え 物理 ぶつり 学 がく 逆 ぎゃく 格子 こうし 応用 おうよう 有限 ゆうげん 次元 じげん 実線 じっせん 型 がた 空間 くうかん 付加 ふか 的 てき 原子 げんし 結晶 けっしょう 位置 いち 符号 ふごう 化 か 束 たば 与 あた 基礎 きそ 群 ぐん 双対 そうつい 性 せい 適用 てきよう
フーリエ級数 きゅうすう 偏 へん 微分 びぶん 方程式 ほうていしき 境界 きょうかい 値 ち 問題 もんだい 解 と 利用 りよう 年 ねん ジョゼフ・フーリエ が初 はじ 方法 ほうほう 熱 ねつ 方程式 ほうていしき 解 と 用 もち 級数 きゅうすう 離散 りさん 版 ばん 標本 ひょうほん 化 か 函数 かんすう 値 ち 等間隔 とうかんかく 並 なら 有限 ゆうげん 個 こ 点 てん 用 もち 場合 ばあい 級数 きゅうすう 有限 ゆうげん 項 こう 値 ね 全 すべ 点 てん 標本 ひょうほん 値 ち 等 ひと 係数 けいすう 全体 ぜんたい 成 な 集合 しゅうごう 与 あた 標本 ひょうほん 列 れつ 離散 りさん 変換 へんかん 英 えい DFT : Discrete Fourier Transformation ) と呼 よ DFT は(レーダー や音声 おんせい 符号 ふごう 化 か 画像 がぞう 圧縮 あっしゅく 応用 おうよう 持 も デジタル信号 しんごう 処理 しょり の重要 じゅうよう 道具 どうぐ 一 ひと 画像 がぞう JPEG は、近 ちか 関係 かんけい 離散 りさん 変換 へんかん 応用 おうよう
高速 こうそく 変換 へんかん 離散 りさん 変換 へんかん 高速 こうそく 計算 けいさん 係数 けいすう 計算 けいさん 畳 たた 込 こ 用 もち 二 ふた 有限 ゆうげん 列 れつ 畳 たた 込 こ 計算 けいさん 利用 りよう ディジタルフィルタ や、巨大 きょだい 整数 せいすう 多項式 たこうしき 高速 こうそく 掛 か 算 ざん (英語 えいご 版 ばん ショーンハーゲ・ストラッセン法 ほう )にも応用 おうよう
二 に 次元 じげん 球面 きゅうめん 点 てん 接 せっ 空間 くうかん 点 てん 球面 きゅうめん 接 せっ 無限 むげん 平面 へいめん 曲面 きょくめん 点 てん 接 せっ 平面 へいめん 自然 しぜん 接点 せってん 原点 げんてん 同一 どういつ 視 し 空間 くうかん 接 せっ 平面 へいめん 接点 せってん 曲面 きょくめん 最適 さいてき 線型 せんけい 近似 きんじ 線型 せんけい 性 せい [nb 14] 三 さん 次元 じげん 空間 くうかん 場合 ばあい 接 せっ 平面 へいめん 基底 きてい 指定 してい 自然 しぜん 方法 ほうほう 点綴 てんてい 的 てき 存在 そんざい 接 せっ 平面 へいめん 実数 じっすう 空間 くうかん 抽象 ちゅうしょう 空間 くうかん 考 かんが 接 せっ 空間 くうかん 高 こう 次元 じげん 可 か 微分 びぶん 多様 たよう 体 たい 一般 いっぱん 化 か
リーマン多様 たよう 体 たい はその接 せっ 空間 くうかん 適当 てきとう 内積 ないせき 備 そな 多様 たよう 体 たい [97] 得 え リーマン曲 きょく 率 りつ は、それ一 ひと 多様 たよう 体 たい 全 すべ 曲 きょく 率 りつ 表 あらわ 一般 いっぱん 相対性理論 そうたいせいりろん 例 たと 時空 じくう 質量 しつりょう 定数 ていすう 記述 きじゅつ アインシュタインテンソル などに応用 おうよう [98] リー群 ぐん の接 せっ 空間 くうかん 自然 しぜん 環 たまき 構造 こうぞう 持 も コンパクト群 ぐん の分類 ぶんるい 用 もち
メビウスの帯 おび 局所 きょくしょ 的 てき U × R 同相 どうしょう ベクトル束 たば は位相 いそう 空間 くうかん X によって連続 れんぞく 的 てき 径 みち 数 すう 付 つ 空間 くうかん 族 ぞく 明確 めいかく 言 い X 上 うえ 束 たば 位相 いそう 空間 くうかん E であって、連続 れんぞく 写像 しゃぞう
π ぱい :
E
→
X
{\displaystyle \pi \colon E\to X}
を持 も X の各 かく 点 てん x においてファイバー V = π ぱい −1 (x )空間 くうかん 成 な 言 い dim V = 1 ならば直線 ちょくせん 束 たば 任意 にんい 空間 くうかん V に対 たい 射影 しゃえい X × V → X 直積 ちょくせき X × V ファイバー束 たば にする。X 上 うえ 束 たば 局所 きょくしょ 性 せい 固定 こてい 空間 くうかん V と X との直積 ちょくせき X の各 かく 点 てん x に対 たい x の適当 てきとう 近傍 きんぼう U を選 えら π ぱい π ぱい −1 (U )制限 せいげん 自明 じめい 束 たば U × V → U 同型 どうけい [nb 15] 局所 きょくしょ 自明 じめい 性 せい 束 たば 巨視的 きょしてき 台 だい 位相 いそう 空間 くうかん X の形 かたち 依存 いぞん 捻 ね 束 たば 自明 じめい 束 たば X × V 大域 たいいき 的 てき 同型 どうけい 必要 ひつよう 例 たと メビウスの帯 おび は(円周 えんしゅう 実数 じっすう 直線 ちょくせん 上 じょう 半開 はんかい 区間 くかん 同一 どういつ 視 し 円周 えんしゅう S 1 上 うえ 線 せん 束 たば 見 み 円筒 えんとう S 1 × R 異 こと 後者 こうしゃ 向 む 付 づ 可能 かのう 性 せい 前者 ぜんしゃ
ある種 しゅ 束 たば 性質 せいしつ 台 たい 位相 いそう 空間 くうかん 情報 じょうほう 提供 ていきょう 例 たと 接 せっ 空間 くうかん 集 あつ 接 せっ 束 たば 可 か 微分 びぶん 多様 たよう 体 たい 点 てん 径 みち 数 すう 付 つ 円周 えんしゅう S 1 接 せっ 束 たば S 1 上 うえ 大域 たいいき 的 てき 非 ひ 零 れい ベクトル場 じょう が存在 そんざい 大域 たいいき 的 てき S 1 × R 同型 どうけい [nb 16] 対照 たいしょう 的 てき 毛 もう 玉 たま 定理 ていり (英語 えいご 版 ばん 二 に 次元 じげん 球面 きゅうめん S 2 上 うえ 接 せっ 場 じょう 至 いた 所 ところ 消 き 者 もの 存在 そんざい K -理論 りろん 同 おな 位相 いそう 空間 くうかん 上 じょう 全 すべ 束 たば 同型 どうけい 類 るい 研究 けんきゅう 深 ふか 位相 いそう 的 てき 幾何 きか 学 がく 的 てき 観察 かんさつ 加 くわ 理論 りろん 実 じつ 有限 ゆうげん 次元 じげん 多元 たげん 体 たい 分類 ぶんるい R , C 四 よん 元 げん 数 すう 体 からだ H 八 はち 元 げん 数 すう 体 からだ O 純 じゅん 代数 だいすう 学 がく 的 てき 帰結 きけつ 存在 そんざい フルヴィッツの定理 ていり (英語 えいご 版 ばん 参照 さんしょう
可 か 微分 びぶん 多様 たよう 多 た 余 よ 接 せっ 束 たば 多様 たよう 体 たい 各 かく 点 てん 接 せっ 空間 くうかん 双対 そうつい 余 よ 接 せっ 空間 くうかん 対応 たいおう 束 たば 余 よ 接 せっ 束 たば 切断 せつだん 1-形式 けいしき (1 -form) と呼 よ
ベクトル空間 くうかん 体 からだ 対 たい 加 か 群 ぐん 英 えい modules 概念 がいねん 環 たまき 対 たい 空間 くうかん 公理 こうり 体 からだ F とするところを環 たまき R で置 お 換 か 得 え 加 か 群 ぐん 理論 りろん 空間 くうかん 比 くら 環 たまき 元 もと 必 かなら 逆 ぎゃく 元 もと 存在 そんざい 複雑 ふくざつ 例 たと 加 か 群 ぐん Z 加 か 群 ぐん アーベル群 ぐん )としての Z /2Z 必 かなら 基底 きてい 持 も 基底 きてい 持 も 加 か 群 ぐん 空間 くうかん 自由 じゆう 加 か 群 ぐん 呼 よ 拘 かか 空間 くうかん 係数 けいすう 環 たまき 体 からだ 加 か 群 ぐん 簡単 かんたん 定義 ていぎ 元 もと 呼 よ 可 か 換 かわ 環 たまき 代数 だいすう 幾何 きか 学 がく 的 てき 解釈 かいしゃく 環 たまき 通 つう ベクトル束 たば の代数 だいすう 的 てき 対応 たいおう 物 ぶつ 局所 きょくしょ 自由 じゆう 加 か 群 ぐん 概念 がいねん 展開 てんかい 可能 かのう
アフィン空間 くうかん 射影 しゃえい 空間 くうかん [ 編集 へんしゅう ] R 3 内 うち アフィン平面 へいめん (水色 みずいろ 二 に 次元 じげん 線型 せんけい 部分 ぶぶん 空間 くうかん x 赤 あか 大雑把 おおざっぱ 言 い アフィン空間 くうかん (英 えい affine space 空間 くうかん 原点 げんてん 正確 せいかく 空間 くうかん 自由 じゆう 推移 すいい 的 てき 空間 くうかん 群 ぐん 作用 さよう 備 そな 集合 しゅうごう 言 い 特 とく 空間 くうかん 写像 しゃぞう
V
×
V
→
V
;
(
v
,
a
)
↦
a
+
v
{\displaystyle V\times V\to V;({\boldsymbol {v}},{\boldsymbol {a}})\mapsto {\boldsymbol {a}}+{\boldsymbol {v}}}
を考 かんが 自身 じしん 上 うえ 空間 くうかん W をベクトル空間 くうかん W のアフィン部分 ぶぶん 空間 くうかん 固定 こてい x W 線型 せんけい 部分 ぶぶん 空間 くうかん V を平行 へいこう 移動 いどう 得 え 言 い 空間 くうかん x V V による W の剰余 じょうよ 類 るい v V 対 たい x v 形 かたち 全 すべ 重要 じゅうよう 例 れい 非 ひ 斉 ひとし 次 じ 線型 せんけい 方程式 ほうていしき 系 けい
A
x
=
b
{\displaystyle A{\boldsymbol {x}}={\boldsymbol {b}}}
の解 かい 空間 くうかん 斉 ひとし 次 つぎ 場合 ばあい b 0 場合 ばあい 一般 いっぱん 化 か 解 かい 空間 くうかん 方程式 ほうていしき 特殊 とくしゅ 解 かい x と、付随 ふずい 斉 ひとし 次 じ 方程式 ほうていしき 解 かい 空間 くうかん A の核 かく 空間 くうかん V に対 たい 部分 ぶぶん 空間 くうかん x V
固定 こてい 有限 ゆうげん 次元 じげん 空間 くうかん V の一 いち 次元 じげん 線型 せんけい 部分 ぶぶん 空間 くうかん 全体 ぜんたい 成 な 集合 しゅうごう 射影 しゃえい 空間 くうかん 呼 よ 平行 へいこう 線 せん 無限 むげん 遠 とお 交 まじ 概念 がいねん 定式 ていしき 化 か 用 もち グラスマン多様 たよう 体 たい (英語 えいご 版 ばん 旗 はた 多様 たよう 体 たい (英語 えいご 版 ばん 決 き 次元 じげん k の線型 せんけい 部分 ぶぶん 空間 くうかん 旗 はた (英語 えいご 版 ばん 呼 よ 線型 せんけい 部分 ぶぶん 空間 くうかん 包含 ほうがん 列 れつ 径 みち 数 すう 付 つ 射影 しゃえい 空間 くうかん 概念 がいねん 一般 いっぱん 化 か
n -次元 じげん 単体 たんたい 標準 ひょうじゅん 凸 とつ 集合 しゅうごう 任意 にんい 多面体 ためんたい 写 うつ 標準 ひょうじゅん (n + 1) 次元 じげん 超 ちょう 平面 へいめん 標準 ひょうじゅん 空間 くうかん 標準 ひょうじゅん (n + 1) 次元 じげん 象限 しょうげん 標準 ひょうじゅん 錐 きり 体 たい 交 まじ 順序 じゅんじょ 体 たい 特 とく 実数 じっすう 体 たい 上 じょう 凸 とつ 解析 かいせき 概念 がいねん 考 かんが 最 もっと 基本 きほん 的 てき 非負 ひふ 線型 せんけい 結合 けつごう 全体 ぜんたい 錐 きり 和 わ 1 となる非負 ひふ 線型 せんけい 結合 けつごう 全体 ぜんたい 凸 とつ 集合 しゅうごう 凸 とつ 集合 しゅうごう 空間 くうかん 公理 こうり 錐 きり 体 たい 公理 こうり 組 く 合 あ 見 み 凸 とつ 集合 しゅうごう 標準 ひょうじゅん 空間 くうかん n -単体 たんたい 超 ちょう 平面 へいめん 象限 しょうげん 交 まじ 反映 はんえい 空間 くうかん 特 とく 線型 せんけい 計画 けいかく 問題 もんだい 用 もち
普遍 ふへん 代数 だいすう 学 がく 言葉 ことば 言 い 空間 くうかん 有限 ゆうげん 和 わ 対応 たいおう 係数 けいすう 有限 ゆうげん 列 れつ 全体 ぜんたい 成 な 普遍 ふへん 空間 くうかん K ∞ 上 うえ 代数 だいすう 一方 いっぽう 空間 くうかん 和 わ 1 の有限 ゆうげん 列 れつ 全体 ぜんたい 成 な 普遍 ふへん 超 ちょう 平面 へいめん 上 じょう 代数 だいすう 錐 きり 体 たい 普遍 ふへん 象限 しょうげん 上 じょう 代数 だいすう 凸 とつ 集合 しゅうごう 普遍 ふへん 単体 たんたい 上 じょう 代数 だいすう 座標 ざひょう 対 たい 可能 かのう 制限 せいげん 和 わ 用 もち 公理 こうり 幾何 きか 化 か
線型 せんけい 代数 だいすう 学 がく 多 おお 概念 がいねん 凸 とつ 解析 かいせき 対応 たいおう 概念 がいねん 基本 きほん 的 てき 基底 きてい 凸 とつ 包 つつみ 形 かたち 生成 せいせい 概念 がいねん 重要 じゅうよう 双対 そうつい 多角 たかく 形 がた 双対 そうつい 錐 きり 極 ごく 錐 きり 双対 そうつい 問題 もんだい 双対 そうつい 性 せい 含 ふく 線型 せんけい 代数 だいすう 学 がく 任意 にんい 空間 くうかん 空間 くうかん 標準 ひょうじゅん 空間 くうかん 同型 どうけい 異 こと 任意 にんい 凸 とつ 集合 しゅうごう 錐 きり 体 たい 単体 たんたい 象限 しょうげん 同型 どうけい 単体 たんたい 多面体 ためんたい 上 うえ 写像 しゃぞう 一般 いっぱん 化 か 重心 じゅうしん 座標 ざひょう 系 けい (英語 えいご 版 ばん 常 つね 存在 そんざい 双対 そうつい 写像 しゃぞう 多面体 ためんたい 面 めん 数 かず 等 ひと 次元 じげん 象限 しょうげん 中 なか 写像 しゃぞう スラック変数 へんすう (英語 えいご 版 ばん 存在 そんざい 同型 どうけい 稀 まれ 多面体 ためんたい 単体 たんたい 象限 しょうげん
^ ここではベクトルをスカラーから区別 くべつ 太字 ふとじ 表 あらわ 特 とく 物理 ぶつり 学 がく 矢印 やじるし 上 うえ 載 の 記法 きほう 広 ひろ 用 もち ラテンアルファベット で表 あらわ グリークアルファベット (ギリシャ文字 もじ 表 あらわ 流儀 りゅうぎ 場合 ばあい 文字種 もじしゅ 区別 くべつ
^ この公理 こうり 演算 えんざん 結合 けつごう 性 せい 仮定 かてい 二 に 種類 しゅるい 乗法 じょうほう 乗法 じょうほう bv 体 からだ 乗法 じょうほう ab との関係 かんけい 性 せい 考 かんが
^ 文献 ぶんけん 例 たと Brown 1991 )係数 けいすう 体 たい R C 制限 せいげん 理論 りろん 大 だい 部分 ぶぶん 変更 へんこう 任意 にんい 体 からだ 上 じょう 成 な 立 た ^ 例 たと 無数 むすう 存在 そんざい 区間 くかん 指示 しじ 函数 かんすう 線型 せんけい 独立 どくりつ ^ この術語 じゅつご 自身 じしん 固有 こゆう 意味 いみ ドイツ語 ご „eigen “ に由来 ゆらい
^ Roman 2005 , p. 140, ch. 8. ジョルダン・シュバレー分解 ぶんかい (英語 えいご 版 ばん 参照 さんしょう ^ 書籍 しょせき Roman 2005 など)この同値 どうち 関係 かんけい 話 はなし 始 はじ 使 つか V /W 具体 ぐたい 形 がた 導 みちび 出 だ 形 かたち ^ この仮定 かてい 得 え 位相 いそう 一様 いちよう 構造 こうぞう 持 も 導 みちび Bourbaki 1989 , ch. II
^ |•|p に関 かん 三角 さんかく 不等式 ふとうしき ミンコフスキーの不等式 ふとうしき から得 え 技術 ぎじゅつ 的 てき 理由 りゆう 文脈 ぶんみゃく ほとんど至 いた 所 ところ 一致 いっち 函数 かんすう 互 たが 同一 どういつ 視 し 上記 じょうき 半 はん 本当 ほんとう ノルム を与 あた
^ 「L 2 属 ぞく 多 おお 函数 かんすう 測度 そくど 有界 ゆうかい 古典 こてん 的 てき 積分 せきぶん 積分 せきぶん 故 ゆえ 可 か 積分 せきぶん 函数 かんすう 空間 くうかん L 2 関 かん 完備 かんび 対 たい 直交 ちょっこう 分解 ぶんかい 適用 てきよう 積分 せきぶん 優位 ゆうい 性 せい 示 しめ Dudley 1989 , p. 125, sect. 5.3
^ p ≠ 2L p Ω おめが 空間 くうかん ^ ヒルベルト空間 くうかん 基底 きてい 既 すで 述 の 線型 せんけい 代数 だいすう 学 がく 的 てき 意味 いみ 基底 きてい 同 おな 意味 いみ 区別 くべつ 後者 こうしゃ ハメル基底 きてい と呼 よ
^ フーリエ級数 きゅうすう 周期 しゅうき 的 てき 手法 しゅほう 任意 にんい 区間 くかん 上 じょう L 2 函数 かんすう 対 たい 函数 かんすう 区間 くかん 外側 そとがわ 周期 しゅうき 的 てき 延長 えんちょう 適用 てきよう Kreyszig 1988 , p. 601
^ これは BSE-3 2001 が言 い 接点 せってん P を通 とお 平面 へいめん 曲面 きょくめん 上 じょう 点 てん P 1 平面 へいめん 距離 きょり 曲面 きょくめん 沿 そ P 1 P に近 ちか 極限 きょくげん P 1 P との距離 きょり 無限 むげん 小 ちい
^ つまり、π ぱい −1 (U )V × U 準 じゅん 同型 どうけい 制限 せいげん 間 あいだ 同型 どうけい 存在 そんざい
^ S 1 接 せっ 束 たば 線 せん 束 たば 自明 じめい 必要 ひつよう 十 じゅう 分 ふん 条件 じょうけん 至 いた 所 ところ 消 き 切断 せつだん 存在 そんざい Husemoller 1994 , Corollary 8.3 を参照 さんしょう 接 せっ 束 たば 切断 せつだん ベクトル場 じょう に他 た
^ “ベクトル空間 くうかん 集合 しゅうごう V と次 つぎ 公理 こうり 満 み 写像 しゃぞう +: V × V → V , ◦: R × V → V からなる三 さん 組 くみ (V , +, ◦) である。” 名古屋大学 なごやだいがく 線形 せんけい 代数 だいすう 学 がく 授業 じゅぎょう 空間 くうかん 年 ねん 。https://www.math.nagoya-u.ac.jp/~larsh/teaching/F2014_LA/lecture1.pdf 。
^ Bourbaki 1998 , Section II .1.1. ブルバキ は群 ぐん 準 じゅん 同型 どうけい f (a )相似 そうじ 英 えい homothety 総称 そうしょう ^ Dorier 1995 ; Moore 1995 ^ 例 たと Lang 1993 , p. 335, ch. XII .3.^ “ベクトル空間 くうかん 有限 ゆうげん 個 こ 組 くみ 生成 せいせい {0 } のとき, V は 有限 ゆうげん 次元 じげん 又 また 有限 ゆうげん 生成 せいせい 東京工業大学 とうきょうこうぎょうだいがく 基底 きてい 存在 そんざい 次元 じげん 年 ねん 。http://www.ocw.titech.ac.jp/?q=201321151&sort=date 。
^ “有限 ゆうげん 次元 じげん 無限 むげん 次元 じげん 東京工業大学 とうきょうこうぎょうだいがく 基底 きてい 存在 そんざい 次元 じげん 年 ねん 。http://www.ocw.titech.ac.jp/?q=201321151&sort=date 。
^ Roman 2005 , Th. 14.3. 米田 よねだ 補題 ほだい 参照 さんしょう ^ representation theory および群論 ぐんろん 参照 さんしょう ^ Folland 1992 , p. 349 ff .^ Jost 2005 . ローレンツ多様 たよう 体 たい も参照 さんしょう ^ Misner, Thorne & Wheeler 1973 , ch. 1.8.7, p. 222 and ch. 2.13.5, p. 325.
線型 せんけい 代数 だいすう 学 がく 関 かん [ 編集 へんしゅう ] Artin, Michael (1991), Algebra , Prentice Hall , ISBN 978-0-89871-510-1 Blass, Andreas (1984), “Existence of bases implies the axiom of choice” , Axiomatic set theory , Contemporary Mathematics, 31 , Providence, RI: American Mathematical Society , pp. 31–33, doi :10.1090/conm/031 , ISBN 0-8218-5026-1 , MR 763890 , http://www.math.lsa.umich.edu/~ablass/bases-AC.pdf Brown, William A. (1991), Matrices and vector spaces , New York: M. Dekker, ISBN 978-0-8247-8419-5 Lang, Serge (1987), Linear algebra , Berlin, New York: Springer-Verlag , ISBN 978-0-387-96412-6 Lang, Serge (2002), Algebra Graduate Texts in Mathematics , 211 (Revised third ed.), New York: Springer-Verlag , ISBN 978-0-387-95385-4 , MR 1878556 , https://books.google.co.jp/books?id=Fge-BwqhqIYC Mac Lane, Saunders (1999), Algebra (3rd ed.), pp. 193–222, ISBN 0-8218-1646-2 Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra SIAM , ISBN 978-0-89871-454-8 , http://www.matrixanalysis.com/ Roman, Steven (2005), Advanced Linear Algebra , Graduate Texts in Mathematics, 135 (2nd ed.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-24766-3 Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups , CRC, ISBN 978-0-8247-9144-5 (ドイツ語 ご van der Waerden, Bartel Leendert (1993), Algebra (9th ed.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-56799-8 解析 かいせき 学 がく 関 かん [ 編集 へんしゅう ] Bourbaki, Nicolas (1987), Topological vector spaces , Elements of mathematics, Berlin, New York: Springer-Verlag , ISBN 978-3-540-13627-9 Bourbaki, Nicolas (2004), Integration I , Berlin, New York: Springer-Verlag , ISBN 978-3-540-41129-1 Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics , Berlin, New York: Springer-Verlag , ISBN 978-0-387-97894-9 BSE-3 (2001), “Tangent plane” , in Hazewinkel, Michiel, Encyclopedia of Mathematics ISBN 978-1-55608-010-4 , https://www.encyclopediaofmath.org/index.php?title=Tangent_plane Choquet, Gustave (1966), Topology , Boston, MA: Academic Press Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists , Courier Dover Publications, ISBN 978-0-486-69193-0 Dudley, Richard M. (1989), Real analysis and probability , The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6 Dunham, William (2005), The Calculus Gallery , Princeton University Press , ISBN 978-0-691-09565-3 Evans, Lawrence C. (1998), Partial differential equations , Providence, R.I.: American Mathematical Society , ISBN 978-0-8218-0772-9 Folland, Gerald B. (1992), Fourier Analysis and Its Applications , Brooks-Cole, ISBN 978-0-534-17094-3 Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets , Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 0-387-98485-2 Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2nd ed.), Harlow, Essex, England: Prentice-Hall (2002発行 はっこう ISBN 0-201-59619-9 Krantz, Steven G. (1999), A Panorama of Harmonic Analysis , Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 0-88385-031-1 Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6th ed.), New York: John Wiley & Sons, ISBN 0-471-85824-2 Kreyszig, Erwin (1989), Introductory functional analysis with applications , Wiley Classics Library, New York: John Wiley & Sons , ISBN 978-0-471-50459-7 , MR 992618 Lang, Serge (1983), Real analysis , Addison-Wesley , ISBN 978-0-201-14179-5 Lang, Serge (1993), Real and functional analysis , Berlin, New York: Springer-Verlag , ISBN 978-0-387-94001-4 Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis , Toronto-New York–London: D. Van Nostrand Company, Inc., pp. x+190 Schaefer, Helmut H. ; Wolff, M.P. (1999), Topological vector spaces (2nd ed.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-98726-2 Treves, François (1967), Topological vector spaces, distributions and kernels , Boston, MA: Academic Press 歴史 れきし 関 かん [ 編集 へんしゅう ] (フランス語 ふらんすご Banach, Stefan (1922), “Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)” , Fundamenta Mathematicae 3 , ISSN 0016-2736 , http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf (ドイツ語 ご Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) , http://dml.cz/handle/10338.dmlcz/400338 (フランス語 ふらんすご Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) , Paris: Hermann Dorier, Jean-Luc (1995), “A general outline of the genesis of vector space theory” , Historia Mathematica 22 (3): 227–261, doi :10.1006/hmat.1995.1024 , MR 1347828 , http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-C&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=2&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=fd995fe2dd19abde0c081f1e989af006 (フランス語 ふらんすご Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur , https://books.google.co.jp/books?id=TDQJAAAAIAAJ&redir_esc=y&hl=ja (ドイツ語 ご Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik , https://books.google.co.jp/books?id=bKgAAAAAMAAJ&pg=PA1&dq=Die+Lineale+Ausdehnungslehre+ein+neuer+Zweig+der+Mathematik&redir_esc=y&hl=ja Grassmann, Hermann (2000), Kannenberg, L.C., ed., Extension Theory , Providence, R.I.: American Mathematical Society , ISBN 978-0-8218-2031-5 Hamilton, William Rowan (1853), Lectures on Quaternions , http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9 (ドイツ語 ご Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) , http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 Moore, Gregory H. (1995), “The axiomatization of linear algebra: 1875–1940” , Historia Mathematica 22 (3): 262–303, doi :10.1006/hmat.1995.1025 , http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-D&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=3&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=4327258ef37b4c293b560238058e21ad (イタリア語 ご Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva , Turin 発展 はってん 的 てき 話題 わだい 関 かん [ 編集 へんしゅう ] Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics , Toronto: Thomson Learning, ISBN 978-0-03-083993-1 Atiyah, Michael Francis (1989), K-theory , Advanced Book Classics (2nd ed.), Addison-Wesley , ISBN 978-0-201-09394-0 , MR 1043170 Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3 , Berlin, New York: Springer-Verlag , ISBN 978-3-540-64243-5 Bourbaki, Nicolas (1989), General Topology. Chapters 1-4 , Berlin, New York: Springer-Verlag , ISBN 978-3-540-64241-1 Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2nd ed.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-96532-1 Eisenberg, Murray; Guy, Robert (1979), “A proof of the hairy ball theorem” , The American Mathematical Monthly 86 (7): 572–574, doi :10.2307/2320587 , JSTOR 2320587 , https://jstor.org/stable/2320587 Eisenbud, David (1995), Commutative algebra , Graduate Texts in Mathematics, 150 , Berlin, New York: Springer-Verlag , MR 1322960 , ISBN 978-0-387-94268-1 , 978-0-387-94269-8 Goldrei, Derek (1996), Classic Set Theory: A guided independent study (1st ed.), London: Chapman and Hall , ISBN 0-412-60610-0 Griffiths, David J. (1995), Introduction to Quantum Mechanics , Upper Saddle River, NJ: Prentice Hall , ISBN 0-13-124405-1 Halmos, Paul R. (1974), Finite-dimensional vector spaces , Berlin, New York: Springer-Verlag , ISBN 978-0-387-90093-3 Halpern, James D. (Jun 1966), “Bases in Vector Spaces and the Axiom of Choice” , Proceedings of the American Mathematical Society (American Mathematical Society) 17 (3): 670–673, doi :10.2307/2035388 , JSTOR 2035388 , https://jstor.org/stable/2035388 Husemoller, Dale (1994), Fibre Bundles (3rd ed.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-94087-8 Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4th ed.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-25907-7 Kreyszig, Erwin (1991), Differential geometry , New York: Dover Publications , pp. xiv+352, ISBN 978-0-486-66721-8 Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8th ed.), New York: John Wiley & Sons , ISBN 0-471-15496-2 Luenberger, David (1997), Optimization by vector space methods , New York: John Wiley & Sons , ISBN 978-0-471-18117-0 Mac Lane, Saunders (1998), Categories for the Working Mathematician Springer-Verlag , ISBN 978-0-387-98403-2 Misner, Charles W. ; Thorne, Kip ; Wheeler, John Archibald (1973), Gravitation ISBN 978-0-7167-0344-0 Naber, Gregory L. (2003), The geometry of Minkowski spacetime , New York: Dover Publications , ISBN 978-0-486-43235-9 , MR 2044239 (ドイツ語 ご Schönhage, A. ; Strassen, Volker (1971), “Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)” , Computing 7 : 281–292, ISSN 0010-485X , http://www.springerlink.com/content/y251407745475773/fulltext.pdf Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two) , Houston, TX: Publish or Perish Stewart, Ian (1975), Galois Theory , Chapman and Hall Mathematics Series, London: Chapman and Hall , ISBN 0-412-10800-3 Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations , Prentice Hall , ISBN 978-0-13-535732-3 Wallace, G.K. (Feb 1992), “The JPEG still picture compression standard”, IEEE Transactions on Consumer Electronics 38 (1): xviii–xxxiv, ISSN 0098-3063 Weibel, Charles A. (1994), An introduction to homological algebra , Cambridge Studies in Advanced Mathematics, 38 , Cambridge University Press , ISBN 978-0-521-55987-4 , OCLC 36131259 , MR 1269324 
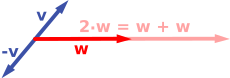

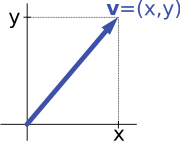



































































![{\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }{\bigl [}a_{m}\cos(mx)+b_{m}\sin(mx){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82598601bc77c6a34bf2324455d7b882e49abb3e)



