统计学 がく 是 ぜ 在 ざい 資料 しりょう 分析 ぶんせき 的 てき 基 もと 研究 けんきゅう 收集 しゅうしゅう 整理 せいり 和 わ 分析 ぶんせき 反映 はんえい 數 すう 據 よりどころ 資料 しりょう 正 せい 息 いき 的 てき 科學 かがく 科 か 自 じ 世 せい 叶 かのう 步 ふ 起 おこり 来 らい 應用 おうよう 在 ざい 各 かく 門 もん 學科 がっか 從 したがえ 自然 しぜん 科学 かがく 社會 しゃかい 科學 かがく 到 いた 人文 じんぶん 學科 がっか 被 ひ 用 よう 工 こう 商業 しょうぎょう 政府 せいふ 的 てき 情報 じょうほう 決 けつ 策 さく 隨 ずい 著 ちょ 大数 たいすう 据 すえ 時代 じだい 來臨 らいりん 統計 とうけい 的 てき 面貌 めんぼう 漸 やや 改變 かいへん 與 あずか 資 し 計算 けいさん 等 とう 領域 りょういき 密 みつ 切 きり 結合 けつごう 是 ぜ 數 かず 據 よりどころ 科學 かがく 中 なか 的 てき 重要 じゅうよう 主軸 しゅじく 之 の 一 いち
譬 たとえ 一 いち 組 くみ 數 すう 據 よりどころ 中 ちゅう 可 か 摘要 てきよう 並 なみ 述 じゅつ 數 すう 據 よりどころ 的 てき 集中 しゅうちゅう 和 わ 離散 りさん 情 じょう 形 がた 用法 ようほう 稱 しょう 作為 さくい 描述統計 とうけい 學 がく 。另外,觀察 かんさつ 者 しゃ 數 かず 據 よりどころ 的 てき 形態 けいたい 建立 こんりゅう 出 で 隨 ずい 機 き 性 せい 和 かず 不 ふ 確定 かくてい 性 せい 的 てき 數學 すうがく 模型 もけい 來 らい 推論 すいろん 研究 けんきゅう 中 ちゅう 的 てき 步 ふ 母體 ぼたい 用 よう 法被 はっぴ 稱 しょう 推論 すいろん 統計 とうけい 學 がく 種 しゅ 用法 ようほう 都 と 可 か 稱 しょう 作為 さくい 應用 おうよう 統計 とうけい 學 がく 數理 すうり 統計 とうけい 學 がく 討論 とうろん 背後 はいご 的 てき 理論 りろん 基礎 きそ 的 てき 學科 がっか
统计可 か 自然 しぜん 和 わ 人文 じんぶん 很多人 じん 学 がく 是 ぜ 一 いち 科学 かがく 的 てき 数学 すうがく 分 ぶん 支 ささえ 是 ぜ 收集 しゅうしゅう 分析 ぶんせき 解 かい 数 かず 据 すえ 的 てき 科学 かがく [ 1] 数学 すうがく 的 てき 一 いち 支 ささえ 因 いん 是 ぜ 收集 しゅうしゅう 解 かい 数 かず 据 すえ 的 てき [ 2] 由 よし 基 もと 重 じゅう 用 よう 学 がく 常 つね 被 ひ 看 み 作 さく 是 ぜ 是 ぜ [ 3] [ 4] 学都 がくと 不 ふ 是 ぜ 数学 すうがく 的 てき 保 ほ 所 しょ 收集 しゅうしゅう 来 らい 的 てき 数 すう 据 すえ 能 のう 得 とく 出 で 有效 ゆうこう 的 てき 将 しょう 数 すう 据 すえ 存 そん 使 し 得 とく 信 しん 息 いき 得 とく 保存 ほぞん 可 か 在国 ざいこく 比 ひ 数 すう 据 すえ 白 しろ 的 てき 意思 いし 采 さい 取 と 必要 ひつよう 保 ほ 据 すえ 来 らい 源 みなもと 的 てき
统计学 がく 家 か 通 どおり 试验设计 和 かず 本来 ほんらい 提 ひさげ 升 ます 数 すう 据 すえ 学 がく 自身 じしん 数 すう 据 すえ 的 てき 概 がい 率 りつ 模型 もけい 提供 ていきょう 了 りょう 工具 こうぐ 学 がく 在 ざい 学 がく 目 め 上 じょう 得 え 到 いた 了 りょう 的 てき 自然 しぜん 科学 かがく 社会 しゃかい 科学 かがく 政府 せいふ 商 しょう 可 か 助 じょ 没 ぼつ 有 ゆう 入 にゅう 公司 こうし 研究 けんきゅう
总结敘述收集 しゅうしゅう 来 らい 的 てき 数 すう 据 すえ 被 ひ 称 しょう 之 の 描述統計 とうけい 學 がく 。这在进行实验研究 けんきゅう 信 しん 息 いき 交流 こうりゅう 中 ちゅう 十 じゅう 分有 ぶんゆう 用 よう 据 すえ 的 てき 分布 ぶんぷ 上 じょう 出 で 上 じょう 的 てき 随 ずい 机 つくえ 性 せい 和 わ 不 ふ 性 せい
將 はた 資料 しりょう 中 ちゅう 的 てき 數 すう 據 よりどころ 模型 もけい 化 か 計算 けいさん 機 き 率 りつ 並 なみ 出 で 對 たい 群 ぐん 體 からだ 的 てき 推論 すいろん 被 ひ 称 しょう 之 の 推論 すいろん 統計 とうけい 學 がく 推論 すいろん 是 ぜ 科学 かがく 的 てき 重 じゅう 要因 よういん 素 もと 因 いん 可能 かのう 机 つくえ 中 ちゅう 得 とく 出 で 数 すう 据 すえ 的 てき 推論 すいろん 統計 とうけい 學 がく 将 はた 命 いのち 行 ぎょう 更 さら 深入 ふかいり 的 てき 研究 けんきゅう 将 はた 都 と 是 ぜ 科学 かがく 方式 ほうしき 的 てき 一 いち 部分 ぶぶん 描述統計 とうけい 學 がく 和 かず 数 すう 据 すえ 的 てき 分析 ぶんせき 更 さら 提供 ていきょう 更 さら 多 た 的 てき 信 しん 息 いき 命 いのち 述 じゅつ 的 てき 真理 しんり
“应用统计学 がく 包括 ほうかつ 描述統計 とうけい 學 がく 和 わ 推論 すいろん 統計 とうけい 學 がく 中 なか 的 てき 成分 せいぶん [ 5] 理 り 重 じゅう 背 せ 后 きさき 的 てき 数理 すうり 学 がく 数理 すうり 学 がく 不 ふ 但 ただし 包括 ほうかつ 法的 ほうてき 概 がい 率 りつ 分布 ぶんぷ 包括 ほうかつ 了 りょう 和 わ 试验设计 。
统计学 がく 与 あずか 概 がい 率 りつ 者 しゃ 地 ち 不同 ふどう 点在 てんざい 概 がい 率 りつ 群 ぐん 體 たい 中 ちゅう 出 で 的 てき 概 がい 率 りつ 好 こう 相反 あいはん 的 てき 中 ちゅう 得 とく 出 で 大 だい 的 てき 母 はは 群 ぐん 體 からだ 的 てき 信 しん 息 いき
统计手法 しゅほう 最早 もはや 可 か 溯 さかのぼ 至 いたり 公 おおやけ 元 もと 前 まえ 世 せい 最早 もはや 的 てき 著作 ちょさく 来 らい 自公 じこう 元 もと 世 せい 密 みつ Manuscript on Deciphering Cryptographic Messages )一 いち 由 ゆかり 阿 おもね 拉 ひしげ 伯 はく 人 じん 肯迪 编著。在 ざい 了 りょう 如何 いか 使用 しよう 数 すう 据 すえ 和 わ 频率分析 ぶんせき 进行密 みつ 根 ね 据 すえ 沙 すな 特 とく 阿 おもね 拉 ひしげ 伯 はく 工程 こうてい 卜 ぼく 拉 ひしげ 阿 おもね 的 てき 学 がく 和 わ 密 みつ 分析 ぶんせき 便 びん 一 いち 同 どう 了 りょう [ 6] [ 7]
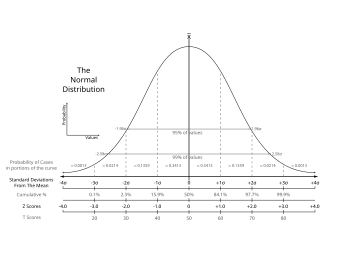
常態 じょうたい 分配 ぶんぱい 的 てき 鐘 かね 型 がた 曲線 きょくせん 的 まと 圖 ず 佛 ふつ 家 か 官 かん 乔瓦尼 あま 尼 あま 编订了 りょう 佛 ふつ 世 せい 史 し Nuova Cronica ,包括 ほうかつ 了 りょう 人口 じんこう 法令 ほうれい 商 しょう 教育 きょういく 宗教 しゅうきょう 在 ざい 内的 ないてき 数 すう 据 すえ 被 ひ 誉 ほまれ 之 の 史上 しじょう 学 がく 入 にゅう 第 だい 一本 いっぽん [ 8] 一 いち 者 しゃ 将 はた 年 ねん 格 かく 根 ね 据 すえ 死亡 しぼう 率 りつ 表 ひょう 出版 しゅっぱん 的 てき 自然 しぜん 与 あずか 政治 せいじ Natural and Political Observations )一书定格为统计学的诞生。[ 9]
統計 とうけい 學 がく 的 てき 英 えい 是 ぜ 源 げん 代 だい 拉 ひしげ 丁 ひのと 國會 こっかい 義 よし 大利 おおとし 國民 こくみん 或 ある 政治 せいじ 家 か 德 とく 最早 もはや 是 ぜ 由 よし 所 しょ 使用 しよう 代表 だいひょう 對 たい 國家 こっか 的 てき 資料 しりょう 進行 しんこう 分析 ぶんせき 的 てき 學問 がくもん 是 ぜ 研究 けんきゅう 國家 こっか 的 てき 科學 かがく 在 ざい 十 じゅう 並 なみ 到 いた 英語 えいご 世界 せかい
統計 とうけい 學 がく 的 てき 初 はつ 作為 さくい 政府 せいふ 通常 つうじょう 是 ぜ 中央 ちゅうおう 政府 せいふ 管理 かんり 階層 かいそう 的 てき 工具 こうぐ 量 りょう 透過 とうか 國家 こっか 國際 こくさい 統計 とうけい 服務 ふくむ 蒐集 しゅうしゅう 國家 こっか 本土 ほんど 的 てき 資料 しりょう 依 よ 照 あきら 各 かく 方面 ほうめん 普 ひろし 提供 ていきょう 關 せき 母體 ぼたい 的 てき 資 し 統計 とうけい 背後 はいご 到 いた 更 さら 多數 たすう 學 がく 導 しるべ 向 むこう 的 てき 領域 りょういき 機 き 率 りつ 或 ある 是 ぜ 從 したがえ 經驗 けいけん 科學 かがく 特別 とくべつ 在 ざい 天文學 てんもんがく 中 ちゅう 獲得 かくとく 的 てき 經驗 けいけん 證據 しょうこ 設定 せってい 參 さん 數 すう 在 ざい 今日 きょう 的 てき 世界 せかい 裡 うら 統計 とうけい 已 やめ 經 けい 被 ひ 使用 しよう 在 ざい 不 ふ 僅僅 きんきん 是 ぜ 國家 こっか 或 ある 政府 せいふ 的 てき 事務 じむ 更 さら 延伸 えんしん 到 いた 商業 しょうぎょう 自然 しぜん 社會 しゃかい 科學 かがく 醫療 いりょう 等 とう 更 さら 多方面 たほうめん 因 よし 為 ため 統計 とうけい 學 がく 擁 よう 有 ゆう 深厚 しんこう 的 てき 歷史 れきし 廣 こう 應用 おうよう 性 せい 統計 とうけい 學 がく 通常 つうじょう 不 ふ 只 ただ 被 ひ 認 みとめ 為 ため 是 ぜ 數學 すうがく 所 ところ 處理 しょり 的 てき 對象 たいしょう 與 あずか 數學 すうがく 本身 ほんみ 的 てき 哲學 てつがく 定義 ていぎ 與 あずか 意義 いぎ 有 ゆう 密 みつ 切 きり 的 てき 關聯 かんれん 許多 きょた 知名 ちめい 的 てき 大學 だいがく 擁 よう 有 ゆう 獨立 どくりつ 的 てき 數理 すうり 統計 とうけい 學 がく 系 けい 統計 とうけい 學 がく 心理 しんり 學 がく 教育 きょういく 学 がく 公共 こうきょう 衛生 えいせい 學 がく 系 けい 中 ちゅう 被 ひ 視 し 為 ため 是 ぜ 一 いち 門主 もんしゅ 科 か
统计学 がく 的 てき 数学 すうがく 基 もと 建立 こんりゅう 在 ざい 世 せい 布 ぬの 和 わ 皮 かわ 埃 ほこり 爾 なんじ 德 とく 費 ひ 馬 ば 的 てき 概 がい 率 りつ 上 うえ 概 がい 率 りつ 研究 けんきゅう 得 どく 来 らい 最小 さいしょう 二 に 乘法 じょうほう 由 ゆかり 卡爾·弗 どる 里 さと 德 とく 里 さと 希 まれ 高 だか 于1794年 ねん 第 だい 一 いち 次 じ 得 とく 出 で 机 つくえ 可 か 行 ぎょう 更 さら 大 だい 尺度 しゃくど 的 てき 生成 せいせい 了 りょう 用 よう 人工 じんこう 的 てき 新 しん 公式 こうしき
费舍尔鸢尾花 はな 数 かず 据 すえ 集 しゅう 之 の 中 ちゅう 花 はな 萼 がく 片 へん 数 すう 据 すえ 的 てき 分布 ぶんぷ 直方 ちょくほう 為 ため 了 りょう 將 しょう 統計 とうけい 學 がく 應用 おうよう 到 いた 科學 かがく 工業 こうぎょう 社會 しゃかい 問題 もんだい 上 じょう 我 わが 研究 けんきゅう 总体 開始 かいし 可能 かのう 是 ぜ 一 いち 個 こ 國家 こっか 的 てき 人民 じんみん 石頭 いしあたま 中 ちゅう 的 てき 水晶 すいしょう 或 ある 者 もの 是 ぜ 某 ぼう 家 か 特定 とくてい 工廠 こうしょう 所 しょ 生產 せいさん 的 てき 商品 しょうひん 由 よし 資料 しりょう 蒐集 しゅうしゅう 所 しょ 組成 そせい 的 てき 母 はは 群 ぐん 體 たい 我 わが 時間 じかん 序列 じょれつ
為 ため 了 りょう 實際 じっさい 的 てき 理由 りゆう 我 わが 選擇 せんたく 研究 けんきゅう 母 はは 群 ぐん 體 からだ 的 てき 子 こ 集 しゅう 代替 だいたい 研究 けんきゅう 母 はは 群 ぐん 體 からだ 的 てき 每 ごと 一 いち 筆 ぴつ 資料 しりょう 子 こ 集 しゅう 稱 しょう 樣 よう 本 ほん 種 しゅ 經驗 けいけん 設計 せっけい 實驗 じっけん 所 しょ 蒐集 しゅうしゅう 的 てき 樣 さま 本 ほん 叫 さけべ 資料 しりょう 資料 しりょう 是 ぜ 統計 とうけい 分析 ぶんせき 的 てき 對象 たいしょう 並 なみ 用 よう 種 しゅ 相關 そうかん 的 てき 用途 ようと 和 わ 推論 すいろん
描述統計 とうけい 學 がく 處理 しょり 有 ゆう 關 せき 的 てき 問題 もんだい 是 ぜ 否 いや 可 か 摘要 てきよう 的 てき 說明 せつめい 資料 しりょう 的 てき 情 じょう 形 がた 不 ふ 論 ろん 是 ぜ 學 がく 或 ある 是 ぜ 圖 ず 片 かた 表現 ひょうげん 來 らい 代表 だいひょう 母 はは 群 ぐん 體 からだ 的 てき 性質 せいしつ 基礎 きそ 的 てき 數學 すうがく 包括 ほうかつ 了 りょう 平均 へいきん 數 すう 和 わ 標準 ひょうじゅん 差 さ 等 ひとし 圖像 ずぞう 的 てき 摘要 てきよう 則 そく 包含 ほうがん 了 りょう 許多 きょた 種 しゅ 的 てき 表 ひょう 和 わ 圖 ず 主要 しゅよう 是 ぜ 說明 せつめい 資料 しりょう 的 てき 集中 しゅうちゅう 和 わ 離散 りさん 情 じょう 形 がた 相關 そうかん 的 てき 觀念 かんねん 特別 とくべつ 被 ひ 出來 でき 討論 とうろん 對 たい 資料 しりょう 集合 しゅうごう 的 てき 統計 とうけい 分析 ぶんせき 可能 かのう 顯示 けんじ 兩個 りゃんこ 變數 へんすう 母 はは 群 ぐん 體 たい 中 ちゅう 的 てき 兩 りょう 種 たね 性質 せいしつ 傾向 けいこう 起 おこり 變動 へんどう 好 こう 像 ぞう 是 ぜ 相 しょう 連 れん 的 てき 一 いち 樣 よう 來 らい 說 せつ 對 たい 收入 しゅうにゅう 和 わ 死亡 しぼう 年齡 ねんれい 的 てき 研究 けんきゅう 期 き 刊 かん 可能 かのう 會 かい 發現 はつげん 窮 きゅう 人 じん 比 ひ 起 おこり 富 とみ 人 じん 平均 へいきん 來 らい 說 せつ 傾向 けいこう 擁 よう 有 ゆう 的 てき 生命 せいめい 兩個 りゃんこ 變數 へんすう 被 ひ 稱 しょう 相關 そうかん 的 てき 但 ただし 是 ぜ 實際 じっさい 上 じょう 我 わが 不能 ふのう 直接 ちょくせつ 推論 すいろん 兩個 りゃんこ 變數 へんすう 中有 ちゅうう 因果 いんが 關係 かんけい 參 まいり 見 み 相關 そうかん 性 せい 推論 すいろん 因果 いんが 關係 かんけい
如果樣 さま 本 ほん 足 あし 代表 だいひょう 母 はは 群 ぐん 體 からだ 的 てき 那 な 樣 さま 本所 ほんじょ 推論 すいろん 和 わ 結論 けつろん 可 か 到 いた 整 せい 個 こ 母 はは 群 ぐん 體 たい 之 の 上 うえ 最大 さいだい 的 てき 問題 もんだい 在 ざい 決定 けってい 樣 さま 本 ほん 是 ぜ 否 ひ 足 あし 代表 だいひょう 整 せい 個 こ 母 はは 群 ぐん 體 たい 統計 とうけい 學 がく 提供 ていきょう 了 りょう 許多 きょた 方法 ほうほう 來 らい 和 わ 修正 しゅうせい 樣 さま 本 ほん 和 わ 蒐集 しゅうしゅう 資料 しりょう 過程 かてい 中 ちゅう 的 てき 隨 ずい 機 き 性 せい 誤差 ごさ 上面 うわつら 所 しょ 提 ひっさげ 到 いた 的 てき 透過 とうか 經驗 けいけん 所 しょ 設計 せっけい 的 てき 實驗 じっけん 參 まいり 見 み 實驗 じっけん 設計 せっけい
要 よう 了解 りょうかい 隨 ずい 機 き 性 せい 或 ある 是 ぜ 機 き 率 りつ 必須 ひっす 具備 ぐび 基本 きほん 的 てき 數學 すうがく 觀念 かんねん 數理 すうり 統計 とうけい 通常 つうじょう 又 また 叫 さけべ 計 けい 理論 りろん 是 ぜ 應用 おうよう 數學 すうがく 的 てき 分 ぶん 支 ささえ 使用 しよう 機 き 率 りつ 論 ろん 來 らい 分析 ぶんせき 並 なみ 證 しょう 統計 とうけい 的 てき 理論 りろん 基礎 きそ
任 にん 何 なん 統計 とうけい 方法 ほうほう 是 ぜ 有效 ゆうこう 的 てき 只 ただ 有 ゆう 當 とう 系統 けいとう 或 ある 是 ぜ 所 しょ 討論 とうろん 的 てき 母 はは 群 ぐん 體 からだ 滿足 まんぞく 方法 ほうほう 論 ろん 的 てき 基本 きほん 假設 かせつ 誤用 ごよう 統計 とうけい 學 がく 可能 かのう 會 かい 導 しるべ 述 じゅつ 面 めん 或 ある 是 ぜ 推論 すいろん 面 めん 嚴重 げんじゅう 的 てき 錯誤 さくご 錯誤 さくご 可能 かのう 會 かい 影響 えいきょう 社會 しゃかい 政策 せいさく 醫療 いりょう 實踐 じっせん 橋 きょう 是 ぜ 核 かく 能 のう 發電 はつでん 計畫 けいかく 結構 けっこう 的 てき 可 か 靠 もたれ 性 せい
即 そく 使 つかい 統計 とうけい 學 がく 被 ひ 正確 せいかく 的 てき 應用 おうよう 結果 けっか 對 たい 是 ぜ 專 せん 家 か 的 てき 人 じん 來 らい 說 せつ 可能 かのう 會 かい 難 なん 陳述 ちんじゅつ 來 らい 說 せつ 統計 とうけい 資料 しりょう 中 ちゅう 顯著 けんちょ 的 てき 改變 かいへん 可能 かのう 是 ぜ 由 ゆかり 樣 さま 本 ほん 的 てき 隨 ずい 機 き 變量 へんりょう 所 しょ 導 しるべ 但 ただし 是 ぜ 顯著 けんちょ 性 せい 可能 かのう 與 あずか 大 だい 言 げん 難 なん 理解 りかい 某 ぼう 統計 とうけい 學 がく 分析 ぶんせき 尤 ゆう 涉 わたる 率 りつ 論 ろん 時 じ 得 とく 出 で 的 てき 結論 けつろん 可能 かのう 非常 ひじょう 違 たがえ 悖 もと 一般人 いっぱんじん 的 てき 直覺 ちょっかく 蒙 こうむ 提 つつみ 問題 もんだい 人 ひと 包括 ほうかつ 一 いち 科學 かがく 家 か 往往 おうおう 需要 じゅよう 統計 とうけい 的 てき 技巧 ぎこう 或 ある 懷疑 かいぎ 才能 さいのう 理解 りかい 確 かく 性 せい
统计研究 けんきゅう 中 ちゅう 的 てき 共同 きょうどう 目 め 分析 ぶんせき 因果 いんが 具体 ぐたい 来 らい 是 ぜ 据 すえ 中 ちゅう 得 とく 出 で 或 ある 是 ぜ 研究 けんきゅう 自 じ 与 あずか 因 いん 之 の 因果 いんが 研究 けんきゅう 主要 しゅよう 有 ゆう 研究 けんきゅう 和 わ 研究 けんきゅう 在 ざい 研究 けんきゅう 中 ちゅう 自 じ 改 あらため 因 いん 所 しょ 造成 ぞうせい 的 てき 影 かげ 不同 ふどう 在 ざい 如何 いか 的 てき 都 と 害 がい 研究 けんきゅう 包括 ほうかつ 将 しょう 系 けい 尺度 しゃくど 研究 けんきゅう 操 みさお 使用 しよう 更 さら 多 た 的 てき 尺度 しゃくど 同 どう 来 らい 操作 そうさ 是 ぜ 否 ひ 改 あらため 尺度 しゃくど 的 てき 与 あずか 之 これ 相 しょう 是 ぜ 研究 けんきゅう 研究 けんきゅう 不 ふ 包括 ほうかつ 性 せい 操作 そうさ 在 ざい 数 すう 据 すえ 被 ひ 收集 しゅうしゅう 数 すう 据 すえ 与 あずか 回 かい 据 すえ 相 あい 数 すう 被 ひ 研究 けんきゅう
统计实验的 てき 基本 きほん 步 ふ 下 か
设立研究 けんきゅう 包括 ほうかつ 代表 だいひょう 研究 けんきゅう 目的 もくてき 数 すう 据 すえ 使用 しよう 信 しん 息 いき 根 ね 据 すえ 效 こう 行 ぎょう 初步 しょほ 假 かり 和 わ 道德 どうとく 上 じょう 的 てき 考 こう 是 ぜ 不可 ふか 少 しょう 的 てき 学 がく 家 か 至 いたり 少 しょう 同 どう 不同 ふどう 目的 もくてき 参照 さんしょう 行 ぎょう 少 すくな 偏差 へんさ
试验设计,使用 しよう 区 く 量 りょう 来 らい 干 ひ 量的 りょうてき 影 かげ 将 はた 随 ずい 机 つくえ 消 しょう 除 じょ 效用 こうよう 与 あずか 中 ちゅう 的 てき 偏差 へんさ 在 ざい 段 だん 参与 さんよ 者 しゃ 和 わ 学 がく 家 か 填 はま 写 うつし 实验草案 そうあん ,并依此指导实验进程 ほど 据 すえ 的 てき 原始 げんし 分析 ぶんせき
根 ね 据 すえ 草案 そうあん 方 かた 差 さ 分析 ぶんせき 在 ざい 第 だい 一 いち 步 ほ 研究 けんきゅう 提出 ていしゅつ 新 しん 假 かり 汇报研究 けんきゅう 对人类行为的实验研究 けんきゅう 多 た 加 か 著名 ちょめい 的 てき 霍桑效 こう 在 ざい 西方 せいほう 電器 でんき 公司 こうし 位 くらい 伊 い 利 り 州 しゅう 的 てき 工 こう 心理 しんり 学 がく 研究 けんきゅう 工作 こうさく 改 あらため 生 なま 的 てき 影 かげ 研究 けんきゅう 人 じん 增强 ぞうきょう 照明 しょうめい 否 いや 有 ゆう 助 じょ 高 だか 流水 りゅうすい 人的 じんてき 生 なま 研究 けんきゅう 人 じん 先 さき 了 りょう 工 こう 生 なま 改 あらため 照明 しょうめい 强度 きょうど 是 ぜ 生 なま 在 ざい 下 か 的 てき 升 ます 了 りょう 然 しか 程 ほど 误差 在 ざい 今 こん 天 てん 特 とく 缺乏 けつぼう 参照 さんしょう 双 そう 盲 めくら 霍桑效 こう 指 ゆび 来 らい 得 とく 出 で 生 なま 的 てき 提 ひさげ 升 ます 不 ふ 是 ぜ 因 いん 照明 しょうめい 强度 きょうど 的 てき 改 あらため 因 いん 人 じん 了 りょう
观察研究 けんきゅう 的 てき 具体 ぐたい 例 れい 子 こ 是 ぜ 研究 けんきゅう 与 あずか 肺癌 はいがん 之 の 相 しょう 数 すう 研究 けんきゅう 常用 じょうよう 来 らい 收集 しゅうしゅう 所 しょ 息 いき 的 てき 行 ぎょう 分析 ぶんせき 在 ざい 本案 ほんあん 例 れい 中 ちゅう 研究 けんきゅう 人 じん 收集 しゅうしゅう 和 わ 不 ふ 者 しゃ 的 てき 数 すう 据 すえ 病 やまい 例 れい 對照 たいしょう 研究 けんきゅう 然 しか 后 きさき 每 ごと 肺癌 はいがん 患者 かんじゃ 的 てき 数量 すうりょう
根據 こんきょ 對 たい 數字 すうじ 的 てき 尺度 しゃくど 分類 ぶんるい 統計 とうけい 學 がく 四 よん 種 しゅ 測量 そくりょう 名目 めいもく 順序 じゅんじょ 等 とう 等比 とうひ 在 ざい 統計 とうけい 過程 かてい 中 ちゅう 各 かく 具有 ぐゆう 不等 ふとう 的 てき 實用 じつよう 性 せい 等比 とうひ 尺度 しゃくど 擁 よう 有 ゆう 零 れい 資料 しりょう 間 あいだ 的 てき 距離 きょり 是 ぜ 相等 そうとう 被 ひ 定義 ていぎ 的 てき 等 とう 尺度 しゃくど 資料 しりょう 間 あいだ 的 てき 距離 きょり 是 ぜ 相等 そうとう 被 ひ 定義 ていぎ 的 てき 但 ただし 是 ぜ 零 れい 非 ひ 絕對 ぜったい 的 てき 無 な 自 じ 行 くだり 定義 ていぎ 的 てき 力 りょく 或 ある 溫度 おんど 的 てき 測量 そくりょう 順序 じゅんじょ 尺度 しゃくど 的 てき 意義 いぎ 並 なみ 非 ひ 表現 ひょうげん 在 ざい 在 ざい 序 じょ 之 の 上 うえ 名目 めいもく 尺度 しゃくど 的 てき 測量 そくりょう 不具 ふぐ 量的 りょうてき 意義 いぎ
对统计信息 いき 的 てき 解 かい 常 つね 涉 わたる 零 れい 假 かり 在 ざい 所有 しょゆう 因 いん 素 もと 量 りょう 都 と 不 ふ 起 おこり 任 にん 何 なん 作用 さよう
对新手 しゅ 来 らい 佳 けい 的 てき 比 ひ 是 ぜ 法 ほう 庭 にわ 了 りょう 零 れい 假 かり 0 认为被告 ひこく 是 ぜ 清白 すずしろ 的 てき 1 则认为被告 ひこく 有罪 ゆうざい 起 おこり 因 いん 被告 ひこく 有罪 ゆうざい 0 (现状)与 あずか 1 对立并且被 ひ 除 じょ 非 ひ 1 被 ひ 超 ちょう 合理 ごうり 的 てき 然 しか 排除 はいじょ 0 ”并不能 ふのう 代表 だいひょう 被告 ひこく 清白 すずしろ 只 ただ 是 ぜ 据 すえ 将 はた 罪 ざい 所以 ゆえん 有 ゆう 必要 ひつよう 在 ざい 0 “无法推翻”的 てき 情 じょう 将 はた 接受 せつじゅ 当 とう 零 れい 假 かり 法被 はっぴ 可 か 强度 きょうど 判断 はんだん 假 かり 否 ひ 近似 きんじ 成立 せいりつ 即 そく 第 だい 二 に 型 がた
在 ざい 零 れい 假 かり 中 ちゅう 存在 そんざい 基本 きほん 误差 :
当 とう 本 ほん 的 てき 偏 へん 中心 ちゅうしん 数 すう 据 すえ 本 ほん 或 ある 母 はは 群 ぐん 體 からだ 平均 へいきん 数 すう 误差 就出现了。许多统计方法 ほうほう 将 はた 中位 ちゅうい 数 すう 乘法 じょうほう 的 てき 最小 さいしょう 化 か 方法 ほうほう 被 ひ 称 しょう 之 の 最小 さいしょう 二 に 乘法 じょうほう
生成 せいせい 数 すう 据 すえ 的 てき 误差 。很多类似误差 被 ひ 是 ぜ 随 ずい 机 つくえ 性的 せいてき 或 ある 是 ぜ 系 けい 偏倚 へんい 性的 せいてき 但 ただし 的 てき 重大 じゅうだい 误差 (如疏忽 ゆるがせ 分析 ぶんせき 填 はま 不 ふ 容 よう 忽 ゆるがせ
许多时候研究 けんきゅう 只 ただ 母 はは 群 ぐん 體 からだ 的 てき 部分 ぶぶん 所以 ゆえん 不能 ふのう 完全 かんぜん 代表 だいひょう 整 せい 群 ぐん 體 たい 任 にん 何 なん 来 らい 自 じ 的 てき 只 ただ 能 のう 得 え 到 いた 母 はは 群 ぐん 體 からだ 的 てき 近似 きんじ 置 おけ 信 しん 区 く 是 ぜ 学 がく 家 か 用 よう 来 らい 表 おもて 述 じゅつ 群 ぐん 體 からだ 真 ま 差 さ 被 ひ 表 ひょう 述 じゅつ 置 おけ 信 しん 区 く 形式 けいしき 上 じょう 数 かず 置 おけ 信 しん 区 く 意味 いみ 着 ぎ 在 ざい 同 どう 重 じゅう 本 ほん 分析 ぶんせき 生成 せいせい 不同 ふどう 的 てき 数 すう 据 すえ 集 しゅう 的 いくわ 区 く 会得 えとく 出 で 符合 ふごう 母 はは 群 ぐん 體 からだ 情 じょう 不 ふ 意味 いみ 着 ぎ 真 ま 概 がい 率 りつ 置 おけ 信 しん 区 く 之 これ 内 ない 率 りつ 角度 かくど 来 らい 的 てき 意 い 因 いん 是 ぜ 一 いち 随 ずい 机 つくえ 真 ま 要 よう 再 さい 的 てき 区 く 然 しか 任 にん 何 なん 数 すう 据 すえ 在 ざい 被 ひ 置 おけ 信 しん 区 く 前 まえ 将 はた 要 よう 被 ひ 的 てき 区 く 的 てき 概 がい 率 りつ 能 のう 代表 だいひょう 真 ま 在 ざい 一 いち 点 てん 上 じょう 区 く 是 ぜ 有 ゆう 待 まち 被 ひ 的 てき 随 ずい 机 つくえ 利用 りよう 信 しん 区 く 出 いで 区 く 概 がい 率 りつ 方法 ほうほう 概 がい 率 りつ 有 ゆう 即 そく 贝叶斯概率 りつ 。
对于给出的 てき 学 がく 回答 かいとう 的 てき 是 ぜ 或 ある 否 ひ 解 かい 常 つね 是 ぜ 显著性差 せいさ 出 で 可 か 零 れい 假 かり 精 せい 概 がい 率 りつ 被 ひ 称 しょう 作 さく 是 ぜ 假定 かてい
显著性差 せいさ 并不一定代表所有的结果在现实世界里都很显著。例 れい 的 てき 研究 けんきゅう 得 とく 出 で 具有 ぐゆう 的 てき 显著性差 せいさ ,但 ただし 是 ぜ 上 じょう 可能 かのう 益 えき 的 てき 不 ふ 会 かい 有效 ゆうこう 地 ち 病人 びょうにん 康 やすし
由 よし 假 かり 中 ちゅう 可能 かのう 更 さら 加 か 偏向 へんこう 一 いち 假 かり 零 れい 假 かり 在 ざい 大 だい 尺度 しゃくど 研究 けんきゅう 中 ちゅう 可能 かのう 会 かい 小差 しょうさ 度 ど 因 いん 中 ちゅう 方法 ほうほう 显著性差 せいさ 所得 しょとく 出 で 的 てき 重大 じゅうだい 差 さ 不 ふ 但 ただし 是 ぜ 我 わが 旧 きゅう 可 か 相 しょう
在 ざい 假 かり 否 いや 被 ひ 显著性差 せいさ 和 わ 不 ふ 代表 だいひょう 效 こう 尺度 しゃくど 更 さら 好 こう 更 さら 常用 じょうよう 的 てき 方法 ほうほう 使 し 置 おけ 信 しん 区 く 是 ぜ 同 どう 的 てき 假 かり 算 さん 中 ちゅう 得 とく 出 で 的 てき 但 ただし 是 ぜ 效 こう 尺度 しゃくど 不 ふ 性 せい 都 と 了 りょう
以下 いか 列 れつ 出 で
有 ゆう 科學 かがく 廣 こう 應用 おうよう 統計 とうけい 的 てき 方法 ほうほう 使 し 得 え 他 た 有 ゆう 各自 かくじ 的 てき 統計 とうけい 術語 じゅつご 學科 がっか 包括 ほうかつ
统计软件gretl 社會 しゃかい 統計 とうけい 包括 ほうかつ 所有 しょゆう 的 てき 社會 しゃかい 科學 かがく 文獻 ぶんけん 統計 とうけい 分析 ぶんせき 化學 かがく 與 あずか 程 ほど 序 じょ 分析 ぶんせき 所有 しょゆう 有 ゆう 關 せき 化學 かがく 的 てき 資料 しりょう 分 ぶん 化工 かこう 科學 かがく 運動 うんどう 統計 とうけい 學 がく 特別 とくべつ 是 ぜ 棒 ぼう 球 だま 曲 きょく 統計 とうけい 對 たい 業 ぎょう 工業 こうぎょう 是 ぜ 一 いち 個 こ 基本 きほん 的 てき 關 せき 鍵 かぎ 他 た 被 ひ 用 もちい 來 らい 了解 りょうかい 與 あずか 測量 そくりょう 系統 けいとう 變異 へんい 性 せい 程 ほど 序 じょ 控 ひかえ 制 せい 對 たい 資料 しりょう 作出 さくしゅつ 結論 けつろん 並 なみ 完成 かんせい 資料 しりょう 取 と 向 こう 的 てき 決 けつ 策 さく 在 ざい 領域 りょういき 統計 とうけい 扮 ふん 演 えんじ 了 りょう 一 いち 個 こ 重要 じゅうよう 的 てき 角 かく 色 しょく
计算机 つくえ 在 ざい 世 せい 半 はん 叶 かのう 的 てき 大量 たいりょう 科学 かがく 了 りょう 的 てき 影 かげ 早期 そうき 模型 もけい 常常 つねづね 為 ため 模型 もけい 但 ただし 强 つよ 机 つくえ 算法 さんぽう 非 ひ 模型 もけい 神 かみ 和 わ 新式 しんしき 算法 さんぽう 廣義 こうぎ 線 せん 性 せい 模 も 式 しき 等 とう 性 せい 模型 もけい 支持 しじ 向 こう 量 りょう 机 つくえ 的 てき 大量 たいりょう
计算机 つくえ 性能 せいのう 的 てき 增强 ぞうきょう 使 し 得 とく 需要 じゅよう 大量 たいりょう 的 てき 再 さい 取 と 法 ほう 成 なり 尚 なお 自助 じじょ 法 ほう 取 と 得 とく 型 がた 更 さら 加 か 可 か 行 ぎょう 机 つくえ 革命 かくめい 使 し 得 とく 在 ざい 未来 みらい 更 さら 加 か 注 ちゅう 重 じゅう 和 かず 大量 たいりょう 普通 ふつう 或 ある 的 てき 面 めん 市 し
同 どう 量 りょう 原点 げんてん 不同 ふどう 看 み 起 おこり 来 らい 差 さ 大 だい 统计数 すう 据 すえ 被 ひ 果 はて 的 てき 解 かい 常 つね 有利 ゆうり [ 10] 与 あずか 可 か 被 ひ 称 しょう 世上 せじょう 有 ゆう 三 さん 言 ごと 的 てき 数字 すうじ 可能 かのう 出 で 意 い 可能 かのう 出 で 故意 こい 如何 いか 用 よう 来 らい 一 いち How to Lie With Statistics )[ 10] 了 りょう 的 てき 与 あずか 中 ちゅう 回 かい 案 あん 例 れい 中 ちゅう 的 てき 方法 ほうほう [ 11]
预防统计滥用包括 ほうかつ 使用 しよう 合 あい 偏差 へんさ [ 12] 当 とう 被 ひ 輕率 けいそつ 概 がい 化 か 超 ちょう 能 のう 代表 だいひょう 的 てき 常 つね 是 ぜ 因 いん 或 ある 故意 こい 忽 ゆるがせ 本 ほん 偏差 へんさ 所 しょ 的 てき [ 13] 条 じょう 形 がた 可能 かのう 是 ぜ 最 さい 容易 ようい 使用 しよう 最 さい 容易 ようい 理解 りかい 的 てき 了 りょう 手 しゅ 或 ある 机 つくえ [ 13] 不 ふ 巧 たくみ 的 てき 是 ぜ 人 じん 忽 ゆるがせ 中 ちゅう 的 てき 偏差 へんさ 因 いん 留意 りゅうい 因 よし 低劣 ていれつ 但 ただし 人 ひと 常 つね 愿 すなお 意 い 去 さ 相 あい 信 しん [ 13] 只 ただ 有 ゆう 当 とう 可 か 代表 だいひょう 才 ざい 是 ぜ 可 か 信 しんじ 精 せい [ 14] 称 しょう 的 てき 可 か 靠 もたれ 性 せい 可 か 偏差 へんさ 破 やぶ 自己 じこ 点 てん 的 てき 空 そら [ 15]
^ Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5 . pp. 1–3
^ Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston, p.xii, ISBN 978-0-03-077945-9
^ Moore, David (1992). "Teaching Statistics as a Respectable Subject". In F. Gordon and S. Gordon. Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. pp. 14–25. ISBN 978-0-88385-078-7 .
^ Chance, Beth L.; Rossman, Allan J. (2005). "Preface". Investigating Statistical Concepts, Applications, and Methods. Duxbury Press. ISBN 978-0-495-05064-3 .
^ Anderson, D.R.; Sweeney, D.J.; Williams, T.A.. (1994) Introduction to Statistics: Concepts and Applications, pp. 5–9. West Group. ISBN 978-0-314-03309-3
^ Al-Kadi, Ibrahim A. (1992) "The origins of cryptology: The Arab contributions”, Cryptologia, 16(2) 97–126. doi:10.1080/0161-119291866801
^ Singh, Simon (2000). The code book : the science of secrecy from ancient Egypt to quantum cryptography (1st Anchor Books ed.). New York: Anchor Books. ISBN 978-0-385-49532-5 .
^ Villani, Giovanni. Encyclopædia Britannica. Encyclopædia Britannica 2006 Ultimate Reference Suite DVD. Retrieved on 2008-03-04.
^ Willcox, Walter (1938) "The Founder of Statistics". Review of the International Statistical Institute 5(4):321–328. JSTOR 1400906
^ 10.0 10.1 Huff, Darrell (1954) How to Lie With Statistics ISBN 978-0-393-31072-6
^ Warne, R. Lazo, M., Ramos, T. and Ritter, N. (2012). Statistical Methods Used in Gifted Education Journals, 2006–2010. Gifted Child Quarterly, 56(3) 134–149. doi :10.1177/0016986212444122
^ Drennan, Robert D. Statistics in archaeology. Pearsall, Deborah M. (编). Encyclopedia of Archaeology . Elsevier Inc. 2008: 2093 –2100. ISBN 978-0-12-373962-9 ^ 13.0 13.1 13.2 Cohen, Jerome B. Misuse of Statistics. Journal of the American Statistical Association (JSTOR). 1938年 ねん 33 (204): 657–674. doi:10.1080/01621459.1938.10502344 ^ Freund, J. F. Modern Elementary Statistics. Credo Reference. 1988. ^ Huff, Darrell; Irving Geis. How to Lie with Statistics . New York: Norton. 1954. The dependability of a sample can be destroyed by [bias]... allow yourself some degree of skepticism.
基本 きほん 概念 がいねん 數學 すうがく 模型 もけい 學習 がくしゅう 範式 はんしき 主要 しゅよう 應用 おうよう 相關 そうかん 領域 りょういき
领域划分 图像类型 相 あい 士 し 相 あい 件 けん
相 あい